基于最大决策熵的快速属性约简算法

Fast Attribute Reduction Algorithm Based on Maximum Decision Entropy

摘要: 在大数据时代背景下，各领域数据爆炸式增长，数据类型复杂多样。针对决策系统中基于最大决策熵的属性约简算法在大规模数据集下运行效率低的问题，提出了一种基于启发式的快速属性约简算法。本文提出的算法首先研究了属性和对象在属性约简过程中的变化对其产生影响，其次提出了属性重要度保序性的相关定理。最后通过UCI数据集对提出算法的有效性进行验证，结果表明提出的快速属性约简算法的运行效率更高。

Abstract: In the era of big data, data in various fields is growing explosively, and data types are complex and diverse. Aiming at the low efficiency of attribute reduction algorithm based on maximum decision entropy in decision system under large data sets, a fast attribute reduction algorithm based on heuristic is proposed. The algorithm proposed in this paper firstly studies the influence of the changes of attributes and objects in the process of attribute reduction, and then puts forward the related theorem about the rank preservation of attributes. Finally, the effectiveness of the proposed algorithm is verified by the UCI data set, and the results show that the proposed fast attribute re-duction algorithm is more efficient.

1. 引言

粗糙集理论是用于处理不精确、不一致、不完备信息和知识的有效工具 [1] [2] 。如今，学者们对粗糙集理论已经进行了深入探索，相应的属性约简 [3] [4] [5] [6] 方法也较为完善。Kryszkiewicz [7] 在不完备决策系统下引入广义决策保持约简，介绍了相关决策规则的提取，并提出了基于差别矩阵的广义决策保持约简方法。差别矩阵方法虽然可以求出所有约简结果，但其效率相对于启发式算法较低。2002年王国胤等 [8] 从信息论观点出发，将条件信息熵作为启发式信息，设计了启发式属性约简算法；2018年，Gao [9] 提出了最大决策熵的启发式属性约简算法。2019年Zhang等 [10] 等提出了启发式的广义决策属性约简。

现阶段，对于大规模数据集，有关属性约简的快速算法研究已取得许多成果。2006年，徐章艳等 [11] 提出了基于基数排序的快速属性约简算法；2010年，Qian等 [12] 提出了正域加速属性约简算法，2018年，Du等 [13] 在序决策系统下提出了快速属性约简算法。另外，增量式属性约简算法 [14] [15] [16] [17] 利用已有的信息进行增量更新，不需要重新计算，从而实现算法效率的提高。本文从对象和属性的角度考虑研究，通过理论分析和实验结果均表明了该算法的有效性。

2. 基本概念

定义1 [1] 信息系统是由四元组 $IS=\left(U,AT,V,f\right)$ 组成，其中U表示论域，是非空有限对象组成的集合；AT表示非空有限属性集合； $V_p$ 表示属性 $p\in AT$ 的值域，有 $V={\displaystyle {\cup }_{P\in AT}{V}_p}$ ；f是一个映射函数， $f:U\times AT\to V$ 为论域U中的每一个对象在 $\forall p\in AT$ 上都有一个值。若 $AT=C\cup D$ ，其中C表示非空有限的条件属性集合，D表示非空有限的决策属性集合，且 $C\cap D\ne \varnothing$ ，则四元组记为 $DS=\left(U,AT=C\cup D,V,f\right)$ 称为决策信息系统。

定义2 [1] 四元组 $DS=\left(U,AT=C\cup D,V,f\right)$ 为一个决策信息系统，对任意非空属性集合 $P\subseteq AT$ ，有

P在U上的不可区分关系定义为：

$IND\left(P\right)=\left\{\left(x,y\right)\in U\times U|p\left(x\right)=p\left(y\right),\forall p\in P\right\}$ (1)

不可区分关系 $IND\left(P\right)$ 是一个满足自反性、对称性和传递性的等价关系。由不可区分关 $IND\left(P\right)$ 导出对论域U的划分为 $U/IND\left(P\right)=\left\{{\left[x\right]}_P|x\in U\right\}$ ，通常简写为U/P，其中 ${\left[x\right]}_P$ 表示包含x的等价类，易得 ${\left[x\right]}_{IND\left(P\right)}={\displaystyle {\cap }_{p\in P}{\left[x\right]}_p}$ 。

定义3 [1] 决策信息系统的四元组 $DS=\left(U,AT=C\cup D,V,f\right)$ ，由决策属性D导出U的划分为 $U/D=\left\{D_1,D_2,\cdots ,D_m\right\}\left(1\le m\le \left|U\right|\right)$ ，对 $\forall P\subseteq C$ ，决策类U/D关于条件属性集P的下近似和上近似的定义为：

$\underset{\_}{P}\left(U/D\right)=\left\{\underset{\_}{P}\left(D_1\right),\underset{\_}{P}\left(D_2\right),\cdots ,\underset{\_}{P}\left(D_m\right)\right\}$ (2)

$\bar{P}\left(U/D\right)=\left\{\bar{P}\left(D_1\right),\bar{P}\left(D_2\right),\cdots ,\bar{P}\left(D_m\right)\right\}$ (3)

决策类U/D关于条件属性集P的正域和边界域的定义：

$PO{S}_P\left(U/D\right)={\displaystyle {\cup }_{D_i\in U/D}\underset{\_}{P}\left(D_i\right)}$ (4)

$BN{D}_P\left(U/D\right)={\displaystyle {\cup }_{D_i\in U/D}\bar{P}\left(D_i\right)}-{\displaystyle {\cup }_{D_i\in U/D}\underset{\_}{P}\left(D_i\right)}$ (5)

定义4 [9] 决策信息系统 $DS=\left(U,AT=C\cup D,V,f\right)$ ，U在C以及D上的划分分别为 $U/C=\left\{U_1,U_2,\cdots ,U_m\right\}$ ， $U/D=\left\{Y_1,Y_2,\cdots ,Y_n\right\}$ ，其中 $m=\left|U/C\right|$ ， $n=\left|U/D\right|$ 。对于任意一个等价类 $U_i\in U/C$ ，

该等价类的最大包含度以及最大决策分别定义为：

$MP\left(D|U_i\right)=\max \left(P\left(Y_1|U_i\right),P\left(Y_2|U_i\right),\cdots ,P\left(Y_n|U_i\right)\right)$ (6)

$MD\left(D|U_i\right)=\left\{f\left(y,D\right)|y\in Y_j\wedge P\left(Y_1|U_i\right)=MP\left(D|U_i\right)\right\}$ (7)

定义5 [9] 决策信息系统 $DS=\left(U,AT=C\cup D,V,f\right)$ ，U在C以及D上的划分分别为 $U/C=\left\{U_1,U_2,\cdots ,U_m\right\}$ ， $U/D=\left\{Y_1,Y_2,\cdots ,Y_n\right\}$ ，其中 $m=\left|U/C\right|$ ， $n=\left|U/D\right|$ 。C相对于D的最大包含度的概

率分布定义为：

$\begin{array}{l}MS\left(D|C\right)=(\left(MP\left(D|U_1\right),1-MP\left(D|U_1\right)\right),\left(MP\left(D|U_2\right),1-MP\left(D|U_2\right)\right),\cdots ,\\ \left(MP\left(D|U_m\right),1-MP\left(D|U_m\right)\right))\end{array}$ (8)

定义6 [9] 决策信息系统 $DS=\left(U,AT=C\cup D,V,f\right)$ ，若 $Q\subseteq C$ ，Q相对于D的最大包含度的概率分布定义为

$MS\left(D|Q\right)=(\left(MP\left(D|U_1\right),1-MP\left(D|U_1\right)\right),\left(MP\left(D|U_2\right),1-MP\left(D|U_2\right)\right),\cdots ,\left(MP\left(D|U_m\right),1-MP\left(D|U_m\right)\right))$ ，那么对于任意一个等价类 $U_i\in U/Q$ 的最大决策熵以及B相对于D的最大决策熵分别定义为：

$MH\left(D|U_i\right)=-P\left(U_i\right)\left(MP\left(D|U_i\right)\log MP\left(D|U_i\right)+\left(m-1\right)\left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\log \left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\right)$ (9)

$MH\left(D|B\right)={\displaystyle \underset{i=1}{\overset{m}{\sum }}MH\left(D|U_i\right)}$ (10)

3. 基于最大决策熵的启发式约简

定义7 [9] 决策信息系统 $DS=\left(U,C\cup D,V,f\right)$ ，若 $Q\subseteq C$ ， $\forall q\in Q$ ，q的内部属性重要度定义为：

$Si{g}_U^{inner}\left(q,Q,C,D\right)=M{P}_C^U\left(D|Q-\left\{q\right\}\right)-M{P}_C^U\left(D|Q\right)$ (11)

定义8 [9] 决策信息系统 $DS=\left(U,C\cup D,V,f\right)$ ，若 $Q\subseteq C$ ， $\forall q\in C-Q$ ，q的外部属性重要度定义为：

$Si{g}_U^{outer}\left(q,Q,C,D\right)=M{P}_C^U\left(D|Q\right)-M{P}_C^U\left(D|Q\cup \left\{q\right\}\right)$ (12)

定义9 [9] 决策信息系统 $DS=\left(U,C\cup D,V,f\right)$ ， $Q\subseteq C$ ， $\forall q\in Q$ ，若 $Si{g}_U^{inner}\left(q,Q,C,D\right)>0$ ，则q为核属性；若 $Si{g}_U^{inner}\left(q,Q,C,D\right)=0$ ，则q为冗余属性。

定义10 [9] 决策信息系统 $DS=\left(U,C\cup D,V,f\right)$ ，若 $Q\subseteq C$ 是C的一个约简，当且仅当满足以下两个

条件：

1) $MH\left(D|Q\right)=MH\left(D|C\right)$ ；

2) 对 $\forall Q^{\prime }\subset Q$ ，有 $MH\left(D|Q^{\prime }\right)\ne MH\left(D|C\right)$ 。

Table 1. Fast reduction algorithm based on maximum decision entropy (ACC_HA_MDE)

表1. 基于最大决策熵的快速约简算法

4. 基于最大决策熵的加速算法

定理1决策信息系统 $DS=\left(U,C\cup D,V,f\right)$ ， $P\subseteq C$ ，若 $\forall a,b\in C-P-P^{\prime }$ ，其中， $C^{\prime }=C-P^{\prime }$ ， $P^{\prime }=\left\{c|M{H}_C^U\left(D|P\right)=M{H}_C^U\left(D|\left(P\cup \left\{c\right\}\right)\right),c\in C-P\right\}$ ， $U^{\prime }=U-PO{S}_P^C\left(U,D\right)$ ，并且 $Si{g}_U^{outer}\left(a,P,C,D\right)\ge Si{g}_U^{outer}\left(b,P,C,D\right)$ ，则 $Si{g}_{U^{\prime }}^{outer}\left(a,P,C^{\prime },D\right)\ge Si{g}_{U^{\prime }}^{outer}\left(b,P,C^{\prime },D\right)$ 。

证明：若 $U/P=\left\{U_1,U_2,\cdots ,U_p,U_{p+1},\cdots ,U_m\right\}$ ， $U/D=\left\{Y_1,Y_2,\cdots ,Y_n\right\}$ ，其中 $U_p,U_{p+1},\cdots ,U_m\subseteq PO{S}_P^C\left(U,D\right)$ 。因此对每个等价类 $U_i\subseteq PO{S}_P^C\left(U,D\right)$ ，存在决策类Y，使 $U_i\cap Y=U_i$ 。用 $M{H}_C^U\left(D|P\right)$ 表示在U上的最大

决策熵。

$\begin{array}{c}M{H}_C^U\left(D|P\right)=-{\displaystyle \underset{i=1}{\overset{m}{\sum }}\left(P\left(U_i\right)\left(MP\left(D|U_i\right)\log MP\left(D|U_i\right)+\left(m-1\right)\left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\log \left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\right)\right)}\\ =-{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(P\left(U_i\right)\left(MP\left(D|U_i\right)\log MP\left(D|U_i\right)+\left(m-1\right)\left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\log \left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\right)\right)}\\ =-\frac{\left|U^{\prime }\right|}{\left|U\right|}{\displaystyle \underset{i=1}{\overset{p}{\sum }}\left(P\left(U_i\right)\left(MP\left(D|U_i\right)\log MP\left(D|U_i\right)+\left(m-1\right)\left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\log \left(\frac{1-MP\left(D|U_i\right)}{m-1}\right)\right)\right)}\\ =\frac{\left|U^{\prime }\right|}{\left|U\right|}M{H}_C^{U^{\prime }}\left(D|P\right)\end{array}$

由于 $U^{\prime }=U-PO{S}_P^C\left(U,D\right)$ ，所以 $PO{S}_P^C\left(U^{\prime },D\right)=\varnothing$ ，又因为 $C^{\prime }=C-P^{\prime }$ ，其中 $P^{\prime }=\left\{c|M{H}_C^U\left(D|P\right)=M{H}_C^U\left(D|\left(P\cup \left\{c\right\}\right)\right),c\in C-P\right\}$ ， $C^{\prime }\cap P^{\prime }=\varnothing$ ， $P\subset P^{\prime }$ ，故 $M{H}_C^U\left(D|P\right)=M{H}_{C^{\prime }}^U\left(D|P\right)$ 。同理可得 $M{H}_C^{U^{\prime }}\left(D|P\right)=M{H}_{C^{\prime }}^{U^{\prime }}\left(D|P\right)$ 。因此 $M{H}_C^U\left(D|P\right)=\left(\left|U^{\prime }\right|/\left|U\right|\right)M{H}_C^{U^{\prime }}\left(D|P\right)=\left(\left|U^{\prime }\right|/\left|U\right|\right)M{H}_{C^{\prime }}^{U^{\prime }}\left(D|P\right)$ ，所以 $Si{g}_U^{outer}\left(a,P,C,D\right)/Si{g}_{U^{\prime }}^{outer}\left(a,P,C^{\prime },D\right)=\left|U^{\prime }\right|/\left|U\right|$ 。因此，若 $Si{g}_U^{outer}\left(a,P,C,D\right)\ge Si{g}_U^{outer}\left(b,P,C,D\right)$ ，则 $Si{g}_{U^{\prime }}^{outer}\left(a,P,C^{\prime },D\right)\ge Si{g}_{U^{\prime }}^{outer}\left(b,P,C^{\prime },D\right)$ 。

通过表1所示的ACC_HA_MDE算法，可以快速计算基于最大决策熵的属性约简。其中ACC_HA_MDE

在步骤5的时间复杂度为 $O\left(a_i{\displaystyle {\sum }_{i=1}^b{\left(b_i-i+1\right)}^2}\right)$ ；而在表2所示的HA_MDE算法在步骤4的时间复杂度为 $O\left(a{b}^2\right)$ 。因此，ACC_HA_MDE的效率更高。

Table 2. Attribute reduction algorithm based on maximum decision entropy (HA_MDE) [9]

表2. 基于最大决策熵的属性约简算法 [9]

5. 实验分析

实验环境采用Intel Corei3-9100 (3.6 GHz)处理器、8 GB内存和Windows10操作系统。算法使用Python语言进行编写，在开发工具PyCharm2020上编译运行。

为了验证提出算法的有效性，本实验选取了8组UCI数据集，为了更好验证所提出算法的有效性，需要对数据集进行预处理。首先将数据集使用WEKA3.8.5进行等频离散化，并将数据集中名词性数据转化为整数表示。对于缺失数据，利用对应属性下占最多比例的属性值进行替换。表3展示了每个数据集的相关信息。在实验过程中，将各数据集按对象数目分成10份(每份为 $\lceil \left|U\right|/10\rceil$ )，或将各数据集的属性每份分成 $\lceil \left|C\right|/10\rceil$ 。

Table 3. Data set information

表3. 数据集信息

约简效率对比

本节对HA_MDE与ACC_HA_MDE两种算法的约简效率进行比较分析，通过8组UCI数据集进行实验展示。表4展示了HA_MDE与ACC_HA_MDE两种算法的时间以及约简长度。可以看到7个数据集的ACC_HA_MDE算法的时间比HA_MDE算法的消耗的时间少。例如Audit-risk数据集，本文提出的算法ACC_HA_MDE耗时0.32 s，而启发式算法HA_MDE运行时间为2.01 s，HA_MDE运行时间约为ACC_HA_MDE运行时间的6.281倍。而Hill数据集，本文提出的算法ACC_HA_MDE相对于HA_MDE耗时较多，由于该数据集在迭代中删除的正域与属性不够多，使消耗时间增多。由于删除的是冗余属性和对象，所以两种算法的约简长度相同。

Table 4. Comparison of time and reduction length of HA_MDE and ACC_HA_MDE algorithms

表4. HA_MDE和ACC_HA_MDE两种算法的时间与约简长度比较

图1中用实心六边形折线表示HA_MDE、用实心倒三角形折线表示ACC_HA_MDE，展示了两种算法在8组数据集上随论域大小变化的时间消耗曲线，横坐标表示论域大小，纵坐标表示算法运行时间。从图1中可以看到除了Hill数据集外，其余7个数据集在本文提出的算法ACC_HA_MDE运行时间相对于HA_MDE运行时间较短。因此，本文提出的ACC_HA_MDE算法相对于启发式HA_MDE算法提高了算法效率。

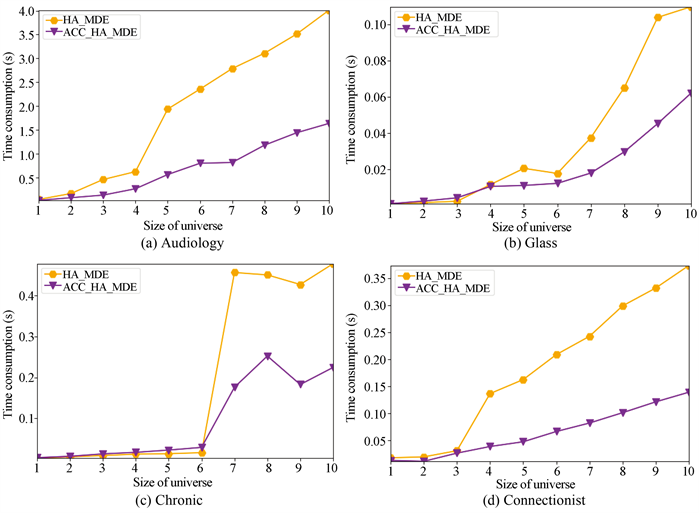
Figure 1. Comparison of algorithm reduction efficiency with object increase

图1. 随着对象增加算法约简效率的比较

6. 总结

本文针对基于最大决策熵的约简目标提出了在完备决策信息系统下的快速属性约简算法。在每轮迭代中首先删除一部分正域，使数据集中对象数目减少，以提高算法的效率；其次删除冗余属性，可以进一步提高算法的效率。实验选取8组UCI数据集对提出的算法进行有效性验证，实验结果表明：本文提出算法的效率优于经典算法的效率，实现了对经典算法的优化。

基金项目

本文受烟台市科技计划项目(编号：2022XDRH016)的资助。