有限差分法和PINN法求解微分方程的探讨

Discussion on Solving Differential Equations by Finite Difference Method and PINN Method

摘要: 在工程实际中的许多问题最终都可以转化为微分方程。由于一些微分方程复杂性，这些方程求解通常具有一定的难度。随着计算机的迅速发展，使得这些方程可以数值求解。如何设计高效的微分方程数值解法尤其重要。微分方程数值解法通常包括有限差分、有限元、有限体积等。近年来基于深度学习的微分方程求解方法十分火热。本文对内嵌物理信息神经网络(PINN)方法进行探讨。我们用传统的有限差分法和PINN法对常微分两点边值问题和偏微分方程中的一类热传导方程进行数值求解，对比分析两种数值解法的优缺点。从数值实验结果中可以看出用PINN相对于传统有限差分法求解微分方程具有更好的精度和效率。

Abstract: Many problems in engineering practice can ultimately be transformed into differential equations. Due to the complexity of some differential equations, solving these equations usually has some dif-ficulty. With the rapid development of computers, these equations can be numerically solved. How to design efficient numerical solutions for differential equations is particularly important. The nu-merical solution of differential equations usually includes finite difference, finite element, finite volume, etc. In recent years, differential equation solving methods based on deep learning have be-come very popular. This article explores the embedded Physics-Informed Neural Networks (PINN) method. We use the traditional finite difference method and the PINN method to numerically solve the ordinary differential two-point boundary value problem and a kind of heat conduction equation in the partial differential equation, and compare the advantages and disadvantages of the two nu-merical methods. From the numerical experiment results, it can be seen that PINN has better accu-racy and efficiency than the traditional finite difference method in solving differential equations.

1. 引言和方法介绍

1.1. 微分方程

微分方程(differential equation)是含有未知函数及其导数(或偏导数)的等式。微分方程包含常微分方程和偏微分方程两类。微分方程广泛应用于物理、工程、生命科学、经济学等领域。例如，在过去战争方式单一时期，微分方程数学模型可以很好地预测战争的局势；而在经济学理论中，微分方程可以分析商品市场价格和需求量的关系，预测和分析一些经济问题；在医学中，微分方程描述事物的动态过程，可以揭示疾病的一些规律，如传染病模型、图像处理 [1] 、癌分析等都用到微分方程。由于方程以及边界条件的复杂性，很难得到微分方程的精确解(解析解)，因此微分方程的数值求解很有必要。

常微分数值求解分为初值问题、边值问题和初值边值混合问题。本文以常微分两点边值问题为例进行讨论。它的数值解法主要有：有限差分法、有限元法、龙格库塔法 [2] 、辛普森法则、伽辽金方法等，它们有不同的特点，我们根据问题选择相应的方法，如果求解的问题较简单，可以用有限差分法或者辛普森法则；如果问题较复杂，可以用有限元法或者龙格–库塔法。偏微分方程传统数值解法主要有：有限差分法、有限元法、有限体积法、边界元法、谱方法、径向基函数方法等。我们要根据问题对这些方法进行选择。如果求解问题简单，就用有限差分法；如果需要高精度和快速收敛速度，就用谱方法或径向基函数方法；如果需要处理复杂的几何形状，就用有限元法或边界元法。本文采用有限差分法。

近年来，通过深度学习求解微分方程愈加火热化，出现的一些比较流行的方法有：物理信息神经网络(PINN) [3] 、神经常微分方程(NODE)、残差神经网络(ResNet)、生成对抗网络(GAN)、变分自编码器(VAE)、卷积神经网络(CNN)等，它们都有各自的优缺点、应用领域和局限。方法的选择也取决于具体问题和可用资源。

本文以内嵌物理信息神经网络PINN方法求解微分方程进行探讨。

1.2. 有限差分法

有限差分法是一种求解微分方程的数值解法。它的原理是利用网格节点逼近导数，并建立有限个未知数的代数方程组来求解各个网格上节点的值。在有限差分法中，我们首先将求解域分成一个个网格单元，每个网格单元上的函数值用一个节点来代表。然后，我们用中心差分公式或向前、向后差分公式来逼近微分方程中的导数，从而得到代表微分方程的离散方程组。通过求解这个离散方程组，我们可以得到每个节点上的函数值，从而得到整个求解域上的函数解。几种常见的差分格式有：

一阶差分格式：

$\frac{\Delta f\left(x\right)}{\Delta x}=\frac{f(x+h-f\left(x\right)}{h}$ ，向前差分 (1)

$\frac{\Delta f\left(x\right)}{\Delta x}=\frac{f\left(x\right)-f\left(x-h\right)}{h}$ ，向后差分 (2)

$\frac{\Delta f\left(x\right)}{\Delta x}=\frac{f\left(x+h\right)-f\left(x-h\right)}{2h}$ ，中心差分 (3)

二阶差分格式：

$\frac{{\Delta }^{2}f\left(x\right)}{\Delta x^2}=\frac{f\left(x+h\right)-2f\left(x\right)+f\left(x-h\right)}{h^2}$ (4)

具体求解步骤可见数值实验部分。那我们就可以知道它的核心是使用差分近似微分，这个过程要舍掉截断误差，预示就产生误差，且无法避免，这个误差量级与选择的差分格式有关。有限差分法的优缺点如下图1：

Figure 1. Plot of advantages and disadvantages of finite difference method

图1. 有限差分法优缺点图

1.3. 深度学习神经网络

深度学习神经网络是一种用于机器学习和人工智能的算法。它由多个层次的神经元组成，可以对大量数据进行训练，以识别图像、语音、文本等信息。

深度学习神经网络的基本结构如图2所示，包括输入层、隐藏层、输出层，是一个前向传播的多层神经网络。在这个网络中，输入数据通过多个隐藏层逐步传递，并被转化为输出结果。每个隐藏层包含多个神经元，每个神经元与上一层的所有神经元相连。每个连接都有一个权重值，用于控制信息流的强度。

Figure 2. Neural network architecture diagram

图2. 神经网络结构图

训练深度学习神经网络通常使用反向传播 [4] 算法。该算法通过比较预测结果与真实结果之间的误差来调整每个连接的权重。通过多次迭代训练，网络逐渐学会提取特征并生成准确的预测结果。

深度学习神经网络已被广泛应用于计算机视觉，如服装图像识别 [5] ，自然语言处理，物理信息预测，如金融预测 [6] ，风电功率预测 [7] 等。

物理信息神经网络(PINN)

PINN (Physics-Informed Neural Networks)是一类用于解决有监督学习任务存在的神经网络，可以在解决物理问题时提高精度和效率。它结合了神经网络和物理方程，并使用已知的物理规律作为约束条件来训练模型。基本原理是将微分方程中的物理约束嵌入到神经网络的训练过程中，以提高模型的精度和泛化能力。PINN使用神经网络来近似未知的物理场，同时也能够满足已知的物理方程，因此可以减少计算成本并提高求解精度。具体地，PINN将物理方程表示为损失函数，并通过反向传播算法来调整神经网络的参数，以最小化损失函数，在某些情况下它比传统方法更准确和高效。PINN的关键在于将物理约束嵌入到神经网络的训练过程中。这样做可以使模型更好地符合实际问题的物理规律，并提高模型的精度和泛化能力。同时，PINN也可以自动处理一些传统数值方法中需要手动调整的参数，例如网格大小和时间步长等。因此，PINN可以在求解微分方程方面具有更好的效率和精度。

但它也存在一些缺点，包括：训练时间长、精度受限、需要大量数据、可解释性差、超参数敏感性等。

2. 常微分两点边值问题数值求解

我们分别用有限差分法和PINN对常微分两点边值问题数值求解，对比了两个方法的精度和效率。

2.1. 有限差分法求解

两点边值问题的一般形式

$\{\begin{array}{l}\frac{\text{d}{}^{2}y}{\text{d}{x}^2}+p\left(x\right)\frac{\text{d}y}{\text{d}x}+q\left(x\right)y=f\left(x\right),0<x<l\\ y\left(0\right)=\alpha ,y\left(l\right)=\beta \end{array}$ (5)

求解步骤(四步法)：

① 网格剖分 将 $\left[0,l\right]$ 剖成 $N+1$ 等份，步长为 $h=l/\left(N+1\right)$ ，节点 $x_i=ih,i=0,1,\cdots ,N+1$ ，

② 将节点 $\left(x_i,t_j\right)$ 代入方程得

$y^{″}\left(x_i\right)+p\left(x_i\right)y^{\prime }\left(x_i\right)+q\left(x_i\right)y\left(x_i\right)=f\left(x_i\right)$ (6)

③ 用差分代替微分，用二阶中心差分和一阶中心差分代替微分即

$y^{″}\left(x_i\right)=\frac{y\left(x_{i+1}\right)-2y\left(x_i\right)+y\left(x_{i-1}\right)}{h^2}+o\left(h^2\right)$ (7)

$y^{\prime }\left(x_i\right)=\frac{y\left(x_{i+1}\right)-y\left(x_{i-1}\right)}{2h}+o\left(h^2\right)$ (8)

带入方程我们得

$\begin{array}{l}\frac{y\left(x_{i+1}\right)-2y\left(x_i\right)+y\left(x_{i-1}\right)}{h^2}+p\left(x_i\right)\frac{y\left(x_{i+1}\right)-y\left(x_{i-1}\right)}{2h}+q\left(x_i\right)y\left(x_i\right)+o\left(h^2\right)=f\left(x_i\right)\\ y\left(x_0\right)=\alpha ,y\left(x_{N+1}\right)=\beta \end{array}$ (9)

④ 舍掉截断误差我们得到：

$\frac{y_{i+1}-2y_i+y_{i-1}}{h^2}+p\left(x_i\right)\frac{y_{i+1}-y_{i-1}}{2h}+q\left(x_i\right)y\left(x_i\right)=f\left(x_i\right)$ (10)

整理以后得到：

$\begin{array}{l}{c}_i{y}_{i+1}+a_i{y}_i+b_i{y}_{i-1}=h^{2}f\left(x_i\right),i=1,2,\cdots ,N\\ y_0=\alpha ,y_{N+1}=\beta \end{array}$ (11)

其中

$a_i=-2+h^{2}q\left(x_i\right),b_i=1-\frac{h}{2}p\left(x_i\right),c_i=1+\frac{h}{2}p(\; x\; i\; )$

因此我们得矩阵方程

$Ay=z$ (12)

其中

$A=\left(\begin{array}{cccccc}{a}_1& c_1& & & & \\ b_2& a_2& c_2& & 0& \\ & b_3& a_3& c_3& & \\ & & \ddots & \ddots & \ddots & \\ & 0& & & a_{N+1}& c_{N+1}\\ & & & & b_N& a_N\end{array}\right)$ , $z=\left(\begin{array}{c}{h}^2{f}_1-\alpha b_1\\ h^2{f}_2\\ ⋮\\ h^2{f}_{N-1}\\ h^2{f}_N-\beta c_N\end{array}\right)$

三对角方程组可采用追赶法求解：

$\begin{array}{l}令w=a_1,y_1=\frac{z_1}{w}\\ v_i=\frac{c_{i-1}}{\omega },w=a_i-b_i{v}_i,y_i=\frac{z_i-b_i{y}_{i-1}}{w},i=2,3,\cdots ,N\\ y_i=y_i-v_{j+1}{y}_{j+1},j=N-1,N-2,\cdots ,1\end{array}$

例2.1 两点边值问题

$\{\begin{array}{l}{y}^{″}-y^{\prime }+y=-\cos x\text{0}<x<\pi \\ y\left(0\right)=0,y\left(\pi \right)=0\end{array}$ (13)

分别取步长 $h=\pi /10,\pi /20,\pi /50$ 得到数值解，并与(13)准确解 $y=\sin x$ 相比较。

解. 此时区间长度等于 $\pi$ ，分别取 $N+1=10,20,50$ ，即步长分别为 $h=\pi /10,\pi /20,\pi /50$

$p\left(x\right)=-1,q\left(x\right)=1,f\left(x\right)=-\cos (\; x\; )$

对应的 $a_i=-2+h^{2}q\left(x_i\right)=-2+h^2,b_i=1-\frac{h}{2}p\left(x_i\right)=1+\frac{h}{2},c_i=1+\frac{h}{2}p\left(x_i\right)=1-\frac{h}{2}$ 。

通过Matlab有限差分编程求解，总的求解时间是0.073758 s，计算结果如图3所示：

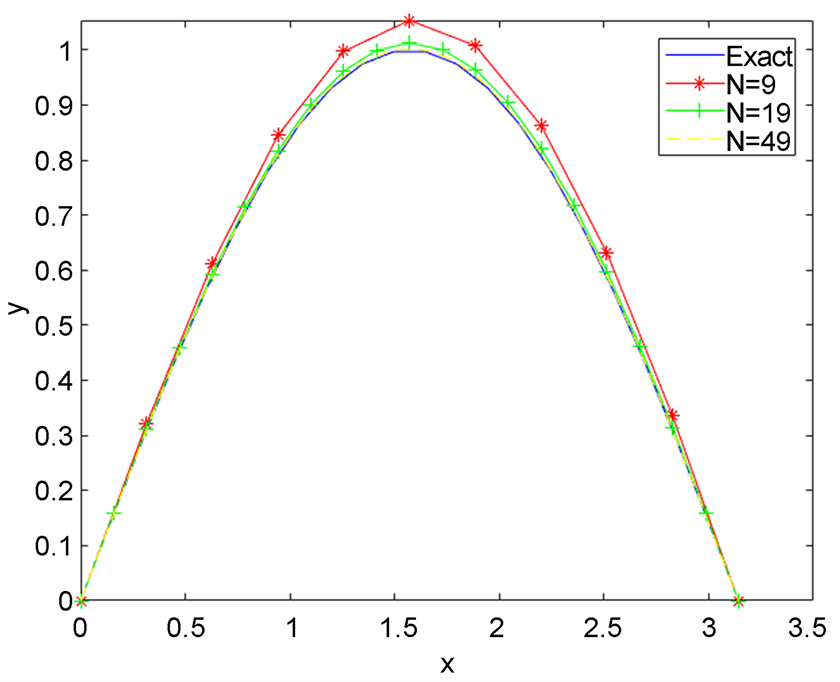
Figure 3. Programming solution results for two-point boundary value problems

图3. 两点边值问题编程求解结果

通过图3，我们发现：随着N = 9，N = 19，N = 49，剖分份数的增加，求解结果与精确解越来越接近，在x = 1.5附近，N = 9求解结果与精确解误差较大；从整体来看在区间两端往区间中间，数值解与精确解之间的误差越来越大，我们再来看x = 1.5附近求解结果的局部放大，如图4所示：

Figure 4. Programming the two-point edge value problem solves the result detail plot

图4. 两点边值问题编程求解结果细节图

从局部放大图4我们可以更加清晰地观察到随着剖分份数N的增加，有限差分求得的数值解与精确解之间的误差越来越小。N = 49的数值逼近效果最好，N = 19的数值逼近效果次之，N = 9的数值逼近效果最差。特别地，误差最大达到10⁻²量级。整体而言数值方法的收敛性良好。同时，使用追赶法求解大规模线性方程组的速度相对较快，但整体误差在 $o\left(h^2\right)$ 量级。

2.2. PINN求解

PINN通过以下几个步骤来求解微分方程：

1) 将微分方程转换为损失函数：将微分方程中的偏微分算子表示为神经网络的输出，并将微分方程中的初始条件和边界条件表示为神经网络的输入。然后，将微分方程和边界条件转换为一个损失函数，用于指导神经网络的训练。

2) 训练神经网络：使用反向传播算法和优化器来最小化损失函数，以更新神经网络的权重和偏置参数。在此过程中，神经网络将自动学习微分方程的解，并逐渐提高模型的精度和泛化能力。

3) 检验结果：使用训练好的神经网络来预测微分方程的解，并与真实解进行比较。如果误差较小，则可以认为神经网络求解了微分方程。

$\{\begin{array}{l}{y}^{″}-y^{\prime }+y=-\cos x,0<x<\pi \\ y\left(0\right)=0,y\left(\pi \right)=0\end{array}$ (14)

我们用PINN再对上面这个常微分两点边值问题进行求解。我们设定一个输入层、3个包含20个神经元的隐藏层和一个输出层，使用双曲正切激活函数和Glorot正态分布初始化方法初始化权重，设定我们的问题域采样点数量为2000，边界采样点数量为10，测试数据集采样点数量为1600，对我们的模型进行10,000次训练周期，使用默认的L-BFGS-B优化器进行微调，绘制出损失历史和训练状态，然后预测出我们的方程区间[0, π]均匀间隔101个点的预测解和残差，训练次数对应的训练损失和测试损失结果见表1。

Table 1. Training loss and test loss corresponding to the number of trainings

表1. 训练次数对应的训练损失、测试损失

从这个表我们可以看出：随着训练周期的增加，我们的训练损失、测试损失越小。而其中最好的模型是设置训练次数为10,122时，它的训练损失为6.44e−08，测试损失为6.12e−08，训练用时为0.904711 s。而在训练次数为10,000时，我们的训练损失和测试损失已经可以达到10⁻⁷量级。具体计算结果见图5。

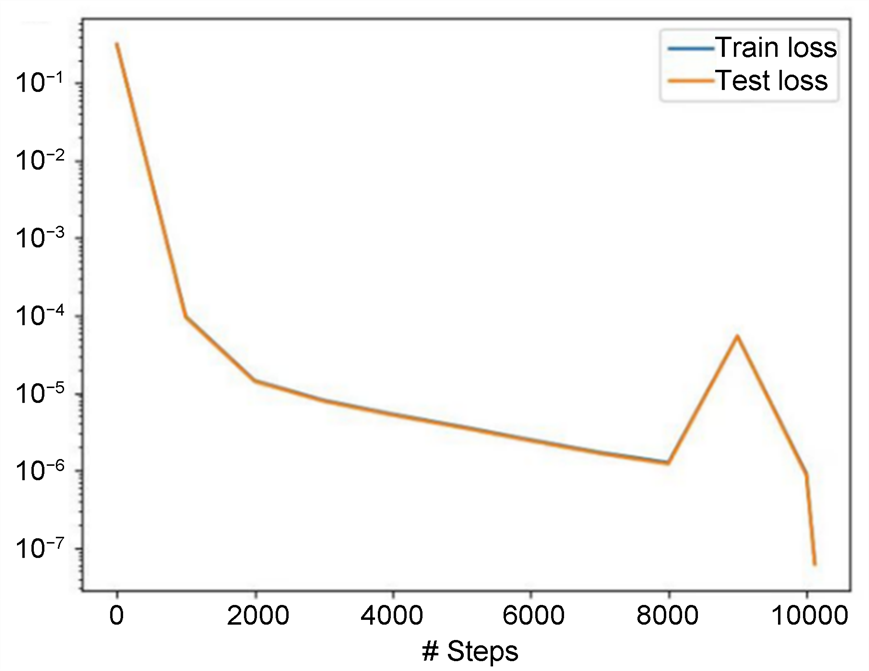
Figure 5. Training and testing loss plots for PINN solving equations

图5. PINN求解方程的训练损失、测试损失图

从图5我们也可以直观地看出迭代次数小于8000时，随着迭代次数的增加，训练损失和测试损失越来越小。而训练次数在8000至10,000之间，训练损失和测试损失进行了一个先增后减的趋势，到迭代次数为10,000时，我们的训练损失和测试损失达到了最小，误差大致在10⁻⁷量级，结果与我们的表格结果一致。

设定迭代次数为10,000，计算机求解时间是0.214267 s，再来看我们求得的预测解、方程的精确解以及它们之间的误差，见图6。

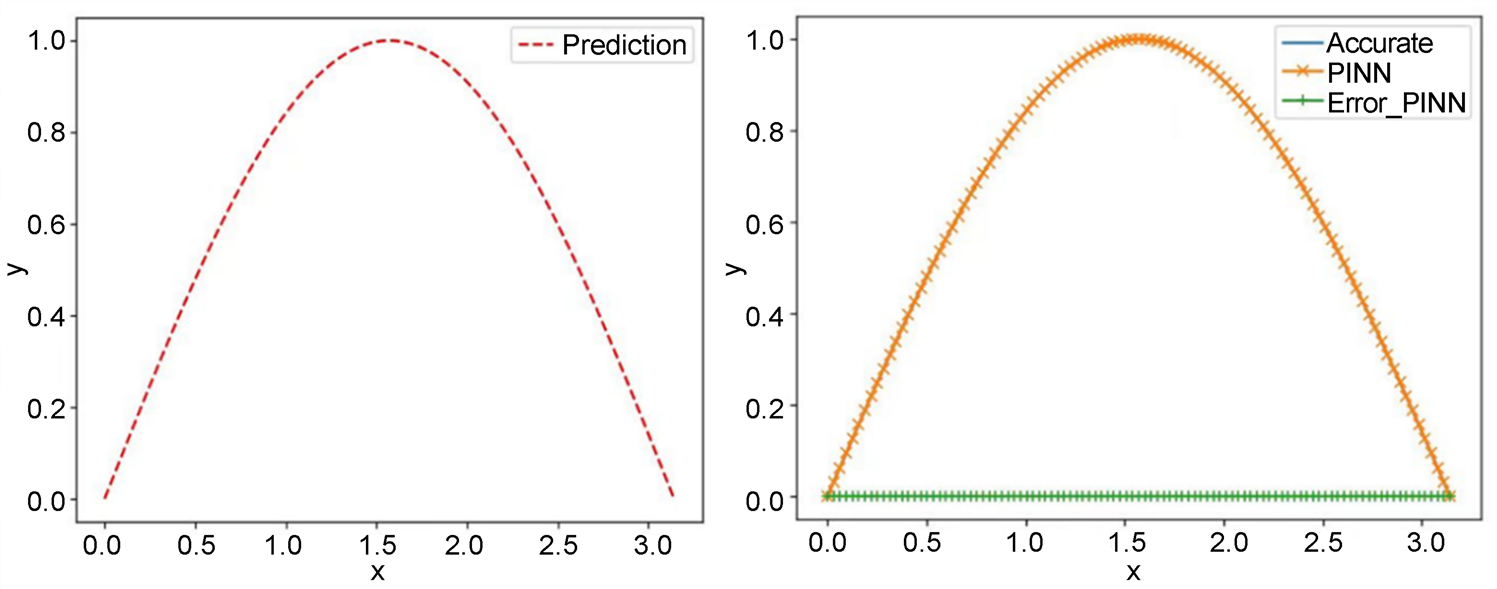
Figure 6. The graph of the predicted solution obtained by PINN, the exact solution of the equation, and the error between them

图6. PINN求得的预测解、方程的精确解及它们之间的误差图

图6的左图是我们用PINN求得的预测解图像，图6的右图为精确解、PINN求得解以及它们之间的误差图。我们可以看出右图中PINN数值解已经把精确解覆盖了。从右图我们也可以看出通过PINN计算的结果和精确解很接近，误差几乎为0。由表1我们知道PINN的误差量级为10⁻⁷，而有限差分法误差量级为10⁻²，故PINN方法比传统有限差分计算精确，但是PINN方法的求解速度上比传统有限差分慢。

综上所述：求解该问题，PINN方法在精度方面要优于传统的有限差分法，但在计算效率(时间)方面不如传统的有限差分法。

3. 热传导方程数值求解

本节，我们分别用有限差分法和PINN对热传导方程数值求解，对比了两个方法的精度和计算效率。

3.1. 有限差分法求解

热传导方程 [8]

$\frac{\partial u}{\partial t}=a\frac{{\partial }^{2}u}{\partial x^2}+f\left(x\right),0<t\le T$ (15)

初始条件：

$u\left(x,0\right)=g\left(x\right),0<x<1$

边界条件：

$u\left(0,t\right)=u\left(1,t\right)=0,0\le t\le T$

求解步骤：

① 网格剖分 将 $\left[0,1\right]$ 剖成 $N+1$ 等份，步长为 $h=1/\left(N+1\right)$ ，节点 $x_i=ih,i=0,1,\cdots ,N+1$ ，将 $\left[0,T\right]$ 剖成M等份，步长 $\tau =T/M$ ，节点 $t_j=ik,i=0,1,\cdots ,M$ 。

② 将节点 $\left(x_i,t_j\right)$ 代入方程得

$u_t\left(x_i,t_j\right)=a{u}_{xx}\left(x_i,t_j\right)+f\left(x_i,t_j\right)$ (16)

③ 用时间向前空间中心差分代替微分

$u_t\left(x_i,t_j\right)=\frac{u\left(x_i,t_{j+1}\right)-u\left(x_i,t_j\right)}{\tau }+o\left(\tau \right),u_{xx}\left(x_i,t_j\right)=\frac{u\left(x_{i+1},t_j\right)-2u\left(x_i,t_j\right)+u\left(x_{i-1},t_j\right)}{h^2}+o\left(h^2\right)$ (17)

代入得

$\frac{u\left(x_i,t_{j+1}\right)-u\left(x_i,t_j\right)}{\tau }+o\left(\tau \right)=a\frac{u\left(x_{i+1},t_j\right)-2u\left(x_i,t_j\right)+u\left(x_{i-1},t_j\right)}{h^2}+o\left(h^2\right)+f\left(x_i,t_j\right)$ (18)

④ 舍掉截断误差可得到如下的差分方程

$令\lambda =\frac{a\tau }{h^2},得u_{i,j+1}=\lambda u_{i+1,j}+\left(1-2\lambda \right)u_{i,j}+\lambda u_{i-1,j}+\tau f_{i,j}$ (19)

$i=1,2,\cdots ,N;j=0,1,\cdots ,M-1;$

$u_{i,0}=g_i,i=1,2,\cdots ,N+1,u_{0,t}=u_{N+1,t}=0,t=1,2,\cdots ,M$

因此

$u_{j+1}=A{u}_j+\tau f_j,j=0,1,2,\cdots ,M-1$ (20)

$A=\left(\begin{array}{cccccc}1-2\lambda & \lambda & & & & \\ \lambda & 1-2\lambda & \lambda & & 0& \\ & \lambda & 1-2\lambda & \lambda & & \\ & & \ddots & \ddots & \ddots & \\ & 0& & & & \lambda \\ & & & & \lambda & 1-2\lambda \end{array}\right)$ ,

$u_j=\left(\begin{array}{c}{u}_{1,j}\\ u_{2,j}\\ ⋮\\ u_{N,j}\end{array}\right),f_j=\left(\begin{array}{c}{f}_{1,j}\\ f_{2,j}\\ ⋮\\ f_{N,j}\end{array}\right),g=\left(\begin{array}{c}{g}_1\\ g_2\\ ⋮\\ g_N\end{array}\right)$

使用追赶法编程求解。它的误差为 $o\left(h^2\right)+o\left(\tau \right)$ 量级。

例3.1热传导方程初边值问题：

$\{\begin{array}{ll}\frac{\partial u}{\partial t}-\frac{{\partial }^{2}u}{\partial x^2}=2,\hfill & 0<x<1,0<t<T,\hfill \\ u\left(x,0\right)=\sin \left(\pi x\right)+x\left(1-x\right),\hfill & 0\le x\le 1,\hfill \\ u\left(0,t\right)=u\left(1,t\right)=0,\hfill & t>0.\hfill \end{array}$ (21)

对于这个问题我们先用有限差分法求解。我们采用时间向前，空间中心的差分格式来求解该问题，

并与精确解 $u\left(x,t\right)={\text{e}}^{-t{\pi }^2}\sin \left(\pi x\right)+x\left(1-x\right)$ 比较。选取时间步长为0.005，空间步长为0.1，进行求解。

此时 $l=1$ ， $N+1=10$ ，空间步长 $h=0.1$ ， $T=0.1$ ， $M=20$ ，时间步长 $\tau =0.005$

$a=1,f\left(i,j\right)=2,g\left(x\right)=\sin \left(\pi x\right)+x\left(1-x\right)$

差分方程为：

$u_{i,j+1}=\lambda u_{i+1,j}+\left(1-2\lambda \right)u_{i,j}+\lambda u_{i-1,j}+2\tau ,\lambda =\frac{\tau }{h^2}=0.5$ (22)

t = 0.1时，总的求解时间是0.090691 s。我们编程求解结果为如图7：

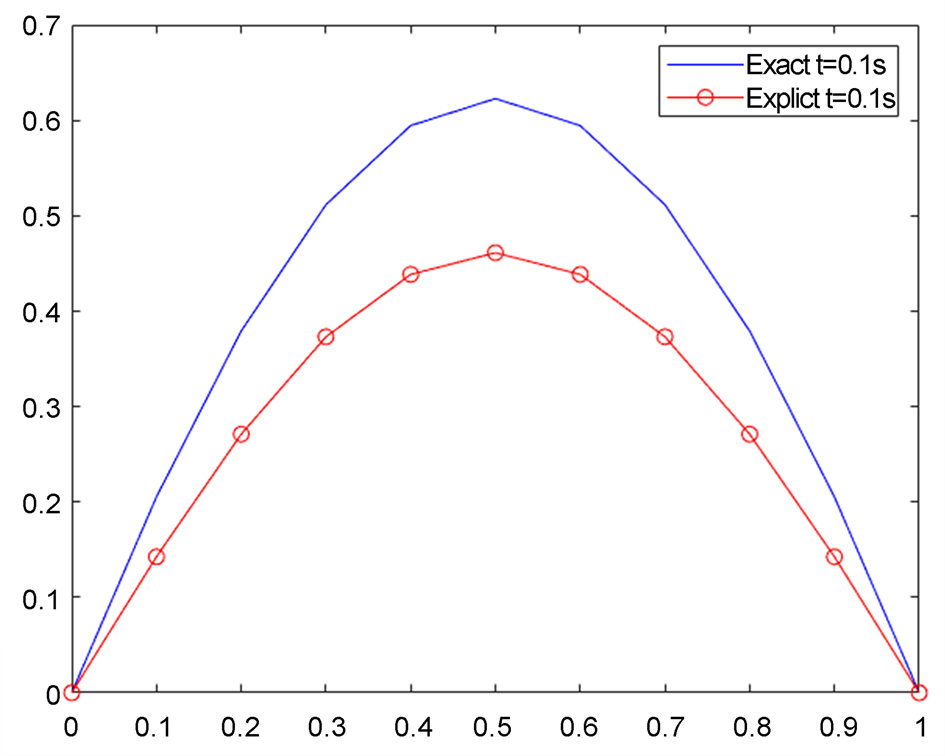
Figure 7. Plot of the analytical solution and exact solution obtained by finite difference method at t = 0.1 s

图7. t = 0.1 s时有限差分法求得的解析解和方程精确解的图

我们把利用有限差分法求得的数值解与该问题的精确解放到一起，即图7。从图7容易很可以发现，数值解和精确解之间的误差在区间中间，即在点x = 0.5附近，达到最大，大致在10⁻¹量级。

3.2. PINN求解

同样我们用PINN再对上面这个热传导问题(21)进行求解。我们设定2个输入层、3个包含20个神经元的隐藏层和一个输出层，使用双曲正切激活函数和Glorot正态分布初始化方法初始化权重，设定我们的问题域采样点数量为2500，边界采样点数量为1000，测试数据集采样点数量为1600，对我们的模型进行10,000次训练周期，设定优化器为Adam指定学习率为1 × 10⁻³，设定迭代次数1000训练模型，再设定优化器L-BFGS-B进一步提高精度，绘制出损失历史和训练状态，然后预测出我们的方程区间 ${\left[0,\pi \right]}^2$ 上均匀间隔101个点在t = 0.1 s的预测解和残差。训练次数对应的训练损失和测试损失结果见表2。

Table 2. Training loss and test loss corresponding to the number of trainings

表2. 训练次数对应的训练损失、测试损失

从表2我们可以看出：随着训练周期的增加，训练损失和测试损失越小。而其中最好的模型是设置训练次数为11,237时，训练损失为6.32e−07，测试损失为6.32e−07，训练用时为0.904711 s。而在训练次数为10,000时，训练损失和测试损失可以达到10⁻⁵量级。具体结果见图8。

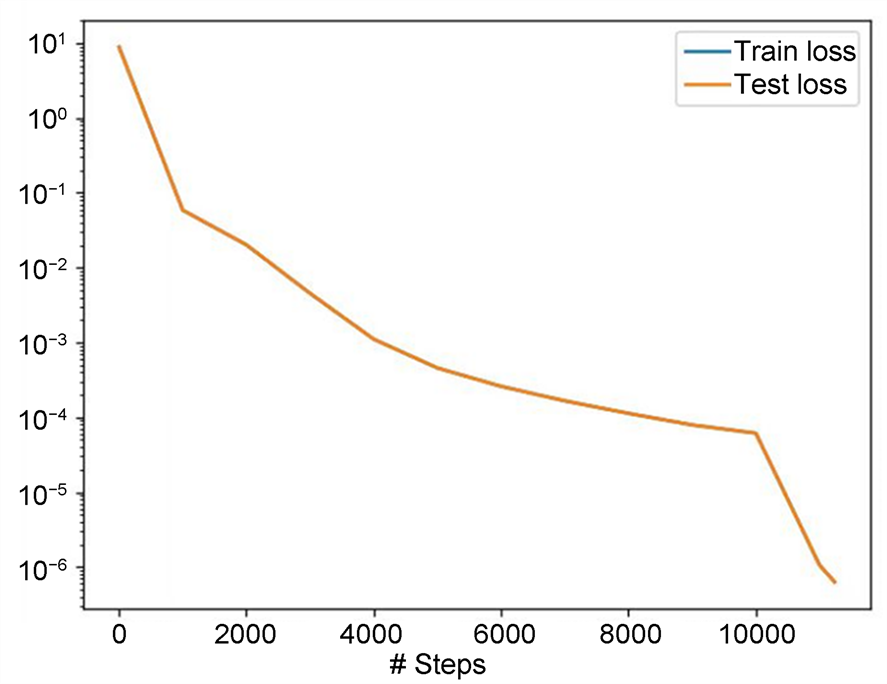
Figure 8. Training and testing loss plots for PINN solving equations

图8. PINN求解方程的训练损失、测试损失图

从图8很容易看出，随着迭代次数的增加，训练损失和测试损失越来越小。迭代次数在10,000次时，损失误差大致是10⁻⁴量级，当迭代次数为11,000时，可以达到10⁻⁶量级。

设定迭代次数为10,000时，计算机求解时间为0.143290 s。再来看我们用PINN求得的预测解、方程的精确解以及它们之间的误差图(图9)。

图9的左图是利用PINN方法求得的预测解图像，图9右图为精确解、PINN求得解以及它们之间的误差图。我们很容易发现，通过PINN方法计算的数值解已经把精确解覆盖了。从右图我们同样可以看出:PINN算得的结果和精确解很接近，误差几乎为0，由表2我们知道，PINN方法的计算误差量级为10⁻⁵，而有限差分法误差量级为10⁻¹。因此PINN法比传统差分法求解精度高,但求解速度不如传统差分法。

综上所述，数值求解热传导方程时，PINN方法在精度上要优于传统有限差分法求解，但在求解效率方面不如传统的有限差分法。

Figure 9. The graph of the predicted solution obtained by PINN, the exact solution of the equation, and the error between them

图9. 通过PINN获得的预测解的图形、方程的精确解以及它们之间的误差

4. 结论与展望

本文基于有限差分法和PINN (物理信息神经网络)方法，以常微分两点边值问题和热传导方程为例，探讨了这两种方法的优缺点，结果表明有限差分法求解速度相对PINN求解要快，但是精度不如PINN方法。基于此，针对不同的微分方程，我们可以根据不同需求选择对应的方法求解。对精度要求高的问题，可以使用PINN法，而对于精度要求不是很高，对求解速度比较高的时候，我们可以采用有限差分法进行求解。

基金项目

河南省高等学校重点科研项目(编号：21B110003)，河南科技大学实验技术开发基金项目(编号：SY2223040)，河南科技大学教改项目(编号：2021KB165)，河南科技大学大学生研究训练计划SRTP (编号：2022226，2023226)。

NOTES

^*通讯作者。