耦合神经元模型中簇放电的动力学分析

Dynamical Analysis of Bursting in a Coupled-Neuron Model

摘要: 呼吸系统是人和动物重要的生理器官之一，位于新生和成年哺乳动物延髓腹外侧区的pre-Bötzinger复合体被认为是呼吸节律产生的中枢，对于研究呼吸系统起着很重要的作用，正常状态和病理状态下呼吸节律有所不同。本文基于pre-Bötzinger复合体耦合神经元模型，利用相平面分析、分岔分析和快慢动力学分析等方法，研究了耦合pre-Bötzinger复合体的簇放电模式及其转迁机制。结果表明钠电导(gNa)对耦合pre-Bötzinger复合体中兴奋性神经元的簇放电节律有重要的影响。

Abstract: Respiratory system is one of the important physiological organs of human and animal. The pre- Bötzinger complex (pre-BötC) is located at a ventrolateral medulla of humans and other mammals, which is considered to be the center for the generation of respiratory rhythms. Respiratory rhythm differs between normal and pathological states, which plays an important role in studying the respiratory system. In this paper, we investigate the bursting and their dynamic mechanisms by phase plane analysis, fast-slow decomposition and bifurcation analysis in coupled-neuron model of the pre-BötC. The results indicate that the Na conductance (gNa) has an important effect on the excitatory neural bursting patterns in the pre-Botzinger complex.

1. 引言

呼吸运动是一种常见的生理活动。1991年，Smith等人发现位于人类和其他哺乳动物脑干的pre-Bötzinger复合体(pre-BötC)似乎是呼吸节律产生的关键部位 [1] 。该复合体包含了所有已知类型的呼吸神经元 [2] 。已有研究表明兴奋性中间神经元的切片起源于前pre-BötC，Rekling等发现这种中间神经元具有类似于心脏起搏器的内在特性 [3] 。此外，Wei等人检测了SST免疫反应性及其与NK1R (神经激肽1受体)在pre-BötC中的突触关系 [4] 。

现代神经元电生理模型的数学框架源于霍奇金和赫胥黎的H-H模型 [5] 。通过一系列设计精妙的实验，发现乌贼巨大轴突中离子电流的产生可以用轴突膜中钠离子和钾离子通道电导率的变化来解释，基于数理科学知识和方法，建立了基于钠离子和钾离子电导随膜电位和时间变化的数学模型，首次建立了描述动作电位产生的一系列微分方程，即霍奇金–赫胥黎模型(H-H模型)，是神经元电生理模型史的重大里程碑。基于霍奇金和赫胥黎提出的离子通道模型，Butera等人建立了描述pre-BötC动作电位的两个最小神经元模型，并研究了耦合神经元的控制和同步 [6] [7] 。在此推动下，Toporikova和Butera在2011年提出了pre-BötC的双室数学模型(TB模型)，其中包括依赖于I_NaP的胞体簇和依赖于I_CAN的树突簇 [8] 。Rubin在2013年改进了TB模型 [9] 。

快慢变量分离以及分岔分析往往可以很好解释神经元系统中不同簇放电模式及其转迁机制 [10] - [15] 。该方法也被应用于研究非神经元系统中的簇和其他现象 [16] [17] [18] 。根据Izhikevich介绍的分类，簇可分为不同类型 [19] 。利用快慢分析和分岔分析，段等人研究了pre-BötC双室模型中钠电导(g_Na)和钾电导(g_K)对簇放电模式及其转迁机制的影响 [20] 。吕等人研究了g_Na和g_K如何影响pre-BötC中MB放电模式，进一步阐明g_K和g_L对MB中的胞体簇个数的影响 [21] 。

为研究动力学模型中不同簇放电模式及其转迁机制，Toporikova和Butera介绍了簇放电的分类 [8] 。参数[IP₃]和持续钠电导(g_NaP)的值对簇放电类型影响很大，若没有Ca²⁺振荡且g_NaP在簇放电的范围内，为胞体簇放电；若Ca²⁺振荡，但g_NaP在亚振荡范围内时，是树突簇放电。除此，还会产生somato-dendritic簇或MB [11] 。

利用快慢分析、分岔分析和Izhikevich的簇分类方案，我们研究了簇放电的产生及其转迁机制随g_Na的变化而发生的转变，对呼吸节律起着重要的作用。

本文结构如下：第二部分，介绍耦合pre-Bötzinger复合体神经元双室模型；第三部分中，探讨g_Na对簇放电的影响，并用快慢分析，分岔分析和峰峰间期(InterSpike Interval, ISI)解释其产生和转迁的动力学机制；最后进行总结。本文中的分岔图是用XPPAUT进行的。

2. 模型介绍

耦合pre-Bötzinger复合体神经元双室模型(TB) [6] [7] [9] [22] 描述如下：

$\text{d}{V}_i/\text{d}t=\left(-I_{\text{NaP}}-I_{\text{CAN}}-I_{\text{Na}}-I_{\text{K}}-I_{\text{L}}-I_{syn-e}-I_{tonic-e}\right)/C_m,$ (1)

$\text{d}{h}_i/\text{d}t=\epsilon \left(h_{\infty }\left(V_i\right)-h_i\right)/{\tau }_h\left(V_i\right),$ (2)

$\text{d}{n}_i/\text{d}t=\left(n_{\infty }\left(V_i\right)-n_i\right)/{\tau }_n\left(V_i\right),$ (3)

$\text{d}{s}_i/\text{d}t={\alpha }_s\left(1-s_i\right)s_{\infty }\left(V_j\right)-s_i/{\tau }_s,$ (4)

钙动力学为

$\text{d}{\left[Ca\right]}_i/\text{d}t=f_m\left(J_{{\text{ER}}_{\text{IN}}}-J_{{\text{ER}}_{\text{OUT}}}\right),$ (5)

$\text{d}{l}_i/\text{d}t=A{K}_d\left(1-l_i\right)-A{\left[Ca\right]}_i{l}_i,$ (6)

其中 $i,j=\left\{1,2\right\}$ 并且 $i\ne j$ 。 $V_i$ 表示膜电位， $h_i$ 和 $n_i$ 是电压依赖性的门控变量， $s_i$ 是突触耦合变量， $l_i$ 表示未被灭活的IP₃通道的部分，该通道会影响由 $J_{{\text{ER}}_{\text{IN}}}$ 和 $J_{{\text{ER}}_{\text{OUT}}}$ 表示的胞浆和内质网(ER)之间钙通量。方程(1)~(6)称为全系统，系统(1)~(3)称为胞体子系统，系统(5)~(6)是树突子系统。各离子电流表达式如下：

$I_{\text{NaP}}=g_{\text{NaP}}{m}_{p,\infty }\left(V_i\right)h_i\left(V_i-E_{\text{Na}}\right),I_{\text{Na}}=g_{\text{Na}}{m}_{\infty }^3\left(V_i\right)\left(1-n_i\right)\left(V_i-E_{\text{Na}}\right),$

$I_{\text{K}}=g_{\text{K}}{n}_i^4\left(V_i-E_{\text{K}}\right),I_{\text{L}}=g_{\text{L}}\left(V_i-E_{\text{L}}\right),I_{tonic-e}=g_{tonic-e}\left(V_i-E_{syn-e}\right),$

$I_{syn-e}=g_{syn-e}{s}_i\left(V_i-E_{syn-e}\right),I_{\text{CAN}}=g_{\text{CAN}}f\left({\left[Ca\right]}_i\right)\left(V_i-E_{\text{Na}}\right),$

其中 $i,j=\left\{1,2\right\}$ 。 $I_{\text{NaP}}$ ， $I_{\text{CAN}}$ ， $I_{\text{Na}}$ ， $I_{\text{K}}$ ， $I_{\text{L}}$ ， $I_{syn-e}$ ， $I_{tonic-e}$ 分别代表持续钠电流，钙激活的非特异性阳离子电流，钠离子电流，钾离子电流，泄露电流，耦合神经元网络连接所产生的电流以及细胞膜受到兴奋性刺激所产生的电流。其它变量的表达式及参数值见附录中表A1。

3. 耦合神经元的同相簇放电

在耦合pre-Bötzinger复合体神经元模型中，簇放电可以分为同相簇放电(初始值相同)与反相簇放电(初始值不同)两种类型。本文主要研究同相簇放电。

3.1. 钠电导对混合簇放电模式的影响

探讨g_Na变化时簇的放电模式及其转迁机制，如图1所示。随着g_Na的增加，系统呈现出不同的放电模式。图中的黑色曲线是膜电位V₁随t的变化趋势，红色曲线为钙离子浓度[Ca]₁随t的变化趋势。随着g_Na的增加，经历了由树突簇，混合簇以及长短峰的循环三种放电模式。

3.2. 簇放电模式的分岔分析

当 $g_{\text{Na}}=3\text{nS}$ 时，[Ca]₁，h₁， $g_{{\text{CAN}}_{\text{Tot}1}}$ 的时间序列如图2(a)所示。黑色、蓝色和红色曲线分别代表[Ca]₁，h₁， $g_{{\text{CAN}}_{\text{Tot}1}}$ 的时间序列。 $g_{{\text{CAN}}_{\text{Tot}i}}$ 是我们添加一个辅助变量 $g_{{\text{CAN}}_{\text{Tot}i}}=g_{\text{CAN}}f\left({\left[Ca\right]}_i\right)$ ，可代替直接使用 ${\left[Ca\right]}_i$ 为分岔参数，其中， $f\left({\left[Ca\right]}_i\right)$ 是一个单调递增的下凹函数，见附录。钙随t产生周期性振荡，每个周期包括两个阶段：静息阶段和尖峰放电阶段。在静息阶段，钙值几乎不变，此时可以认为钙是一个常数，取[Ca]₁的平均值，为 ${\left[Ca\right]}_1=0.026\text{μM}$ 。在尖峰放电阶段，钙的波动比h₁的大，此时可以认为h₁是常数，钙是慢变量。类似的，部分具有代表性的簇放电也选择合适的慢变量进行分岔分析。

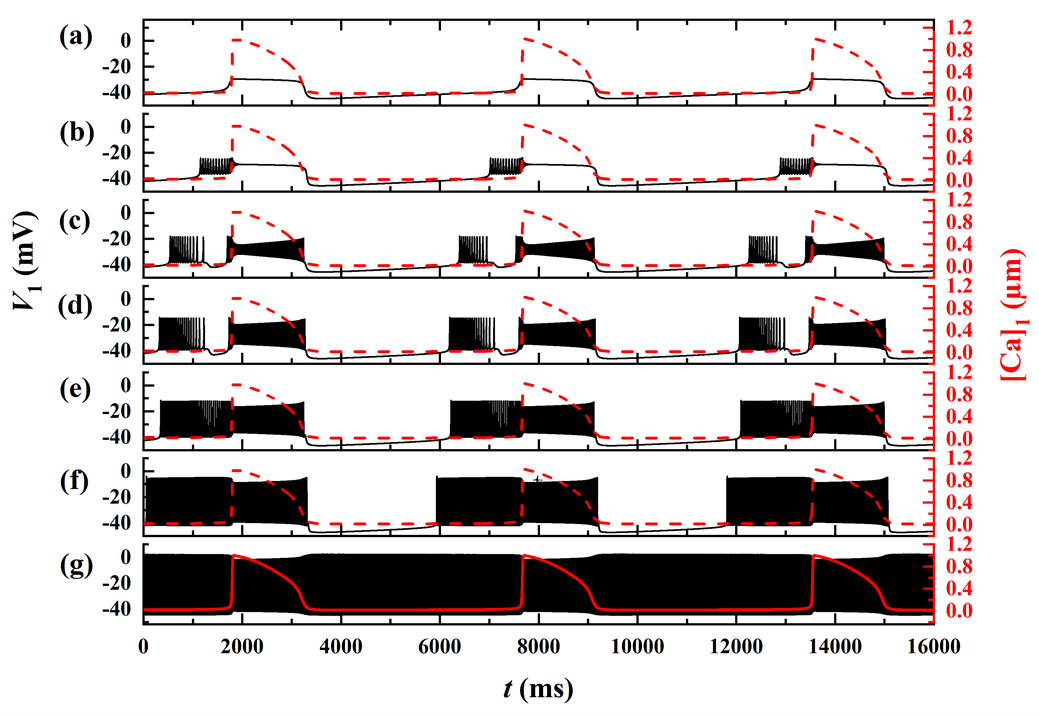
Figure 1. In-phase bursting of the system. (a) $g_{\text{Na}}=1\text{nS}$ ; (b) $g_{\text{Na}}=2\text{nS}$ ; (c) $g_{\text{Na}}=3\text{nS}$ ; (d) $g_{\text{Na}}=4\text{nS}$ ; (e) $g_{\text{Na}}=5\text{nS}$ ; (f) $g_{\text{Na}}=10\text{nS}$ ; (g) $g_{\text{Na}}=20\text{nS}$

图1. 同相簇放电模式。(a) $g_{\text{Na}}=1\text{nS}$ ；(b) $g_{\text{Na}}=2\text{nS}$ ；(c) $g_{\text{Na}}=3\text{nS}$ ；(d) $g_{\text{Na}}=4\text{nS}$ ；(e) $g_{\text{Na}}=5\text{nS}$ ；(f) $g_{\text{Na}}=10\text{nS}$ ；(g) $g_{\text{Na}}=20\text{nS}$

树突子系统(5)-(6)的零等值线和周期轨迹如图2(b)所示。其中，红色和蓝色曲线分别代表变量[Ca]₁、 $l_1$ 的零等值线。黑色封闭曲线表示树突子系统的周期轨迹(顺时针方向)。轨迹在树突子系统离开五角星区域(★)后，开始快速振荡，树突子系统的轨迹沿着[Ca]₁零等值线的右分支向下移，[Ca]₁也会随之缓慢减小，然后跳至零等值线的左分支，最终回到五角星区域(★)。

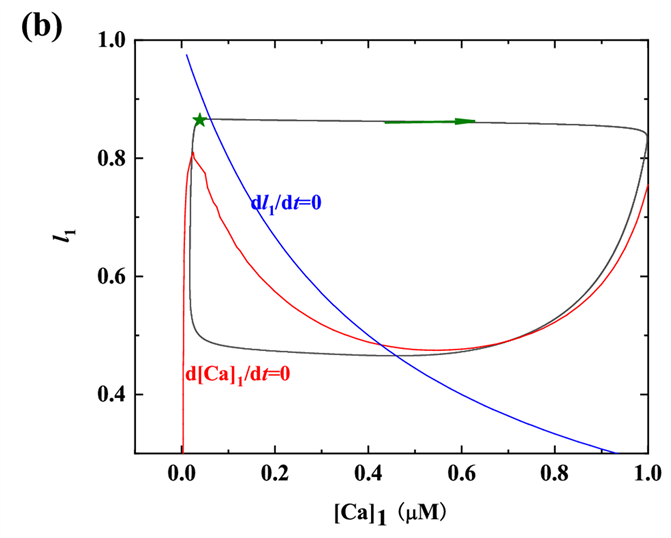
Figure 2. (a) Time series diagram of [Ca]₁, h₁, $g_{{\text{CAN}}_{\text{Tot1}}}$ vs. t when $g_{\text{Na}}=3\text{nS}$ ; (b) The periodic orbit in the dendritic subsystem when $g_{\text{Na}}=3\text{nS}$

图2. (a) $g_{\text{Na}}=3\text{nS}$ 时[Ca]₁，h₁， $g_{{\text{CAN}}_{\text{Tot1}}}$ 的时间序列图；(b) 当 $g_{\text{Na}}=3\text{nS}$ 时树突子系统中的周期轨线

$g_{\text{Na}}=3\text{nS}$ 时，全系统的膜电位V₁ (黑色曲线)随t的变化趋势如图3(a)所示。此时每个周期内有两种不同类型的簇放电，为混合簇放电(MB)。根据树突子系统动力学的不同将每个周期分为两个阶段。第一个阶段是从星号(⋆)到实心圆(•)的时期，第二个阶段是从实心圆(•)到方块( $■$ )的时期。据[Ca]₁振荡的动力学特性，混合簇放电包括胞体簇放电(第一个阶段)和树突簇放电(第二个阶段) [21] 。树突系统中不同神经元的钙动力学是相同的，所以 ${\left[Ca\right]}_1={\left[Ca\right]}_2$ 。

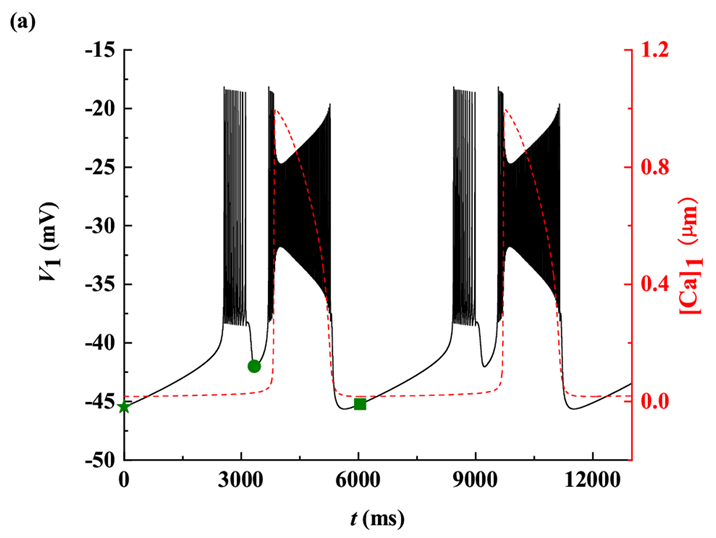
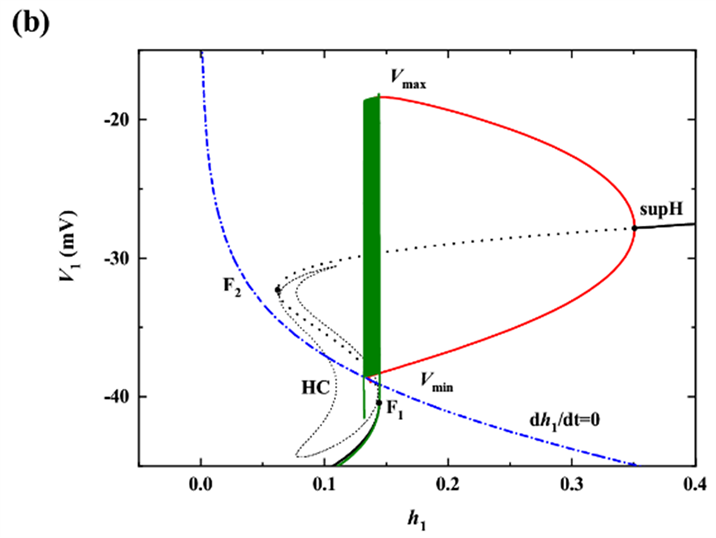
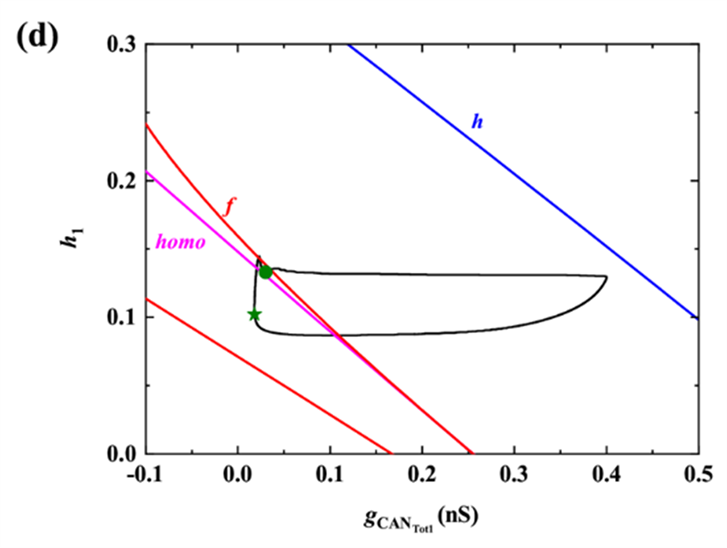
Figure 3. One and two-parameter bifurcation analysis of bursting with $g_{\text{Na}}=3\text{nS}$ . (a) Time series of membrane potential V₁ (black curve); (b) Bifurcation structure of the fast subsystem for the somatic bursting; (c) Bifurcation structure of the fast subsystem for the dendritic bursting; (d) Two-parameter bifurcation of the fast subsystem with respect to the slow variable $g_{{\text{CAN}}_{\text{Tot}1}}$ and h₁

图3. $g_{\text{Na}}=3\text{nS}$ 时的单参数和双参数分岔分析。(a) 膜电位V₁ (黑色曲线)的时间序列；(b) 胞体簇的单参数分岔分析；(c) 树突簇的单参数分岔分析；(d) 簇放电的双参数( $h_1,g_{{\text{CAN}}_{\text{Tot}1}}$ )分岔分析

$g_{\text{Na}}=3\text{nS}$ 时以h₁为慢变量对胞体簇进行分岔分析，对应快子系统的分岔如图3(b)所示。(其中(b)，(c)中黑色实线(虚线)表示稳定(不稳定)平衡点，红色实线(虚线)表示稳定(不稳定)的周期轨道，F₁、F₂表示平衡点的鞍结分岔，supH表示超临界Hopf分岔，HC表示同宿轨分岔，绿色曲线表示全系统轨线，下同。)随h₁的增大，下支的静息态经由鞍结分岔(F₁)跃迁至上支的稳定极限环，并由于稳定极限环的吸引和不稳定焦点的排斥反复振荡，最终经由极限环上的同宿轨分岔(HC)回到下支的静息态。据Izhikevich簇放电分类的标准 [23] ，此时的簇放电模式为“fold/homoclinic”型簇放电。

对于树突簇，此时由上文分析，可选择 $g_{{\text{CAN}}_{\text{Tot}1}}$ 为慢变量进行分岔分析，如图3(c)所示。下支的静息态经由鞍结分岔(F₁)跃迁至上支，由于supH产生的稳定极限环的吸引和不稳定焦点的排斥作用，轨线绕着不稳定焦点旋转且振幅逐渐增大，最后经过极限环上同宿轨分岔(HC)回到下支的静息态，因此，簇放电模式为“Hopf/homoclinic”型簇放电。

快子系统在 $\left(h_1,g_{{\text{CAN}}_{\text{Tot}1}}\right)$ 平面上的双参数分岔如图3(d)所示，f，homo，h分别代表鞍结分岔曲线(红色)，同宿轨分岔曲线(紫色)，以及Hopf分岔曲线(蓝色)。随着慢变量 $g_{{\text{CAN}}_{\text{Tot}1}}$ 的逐渐增加，全系统轨线(绿色曲线)在分岔曲线f和homo之间来回跃迁，意味着混合簇中胞体簇的产生与这两类分岔密切相关。全系统轨线在分岔曲线f和homo之间跃迁一次，对应于混合簇中的一个胞体簇。之后， $g_{{\text{CAN}}_{\text{Tot}1}}$ 的突增，使混合簇的胞体部分结束，进入树突部分。

当g_Na增加至5 nS时，类似于 $g_{\text{Na}}=3\text{nS}$ 时的分析过程，以h₁为慢变量对胞体簇进行分岔分析，对应快子系统的分岔如图4(b)所示。该簇放电模式为“fold/homoclinic”型簇放电。树突簇如图4(c)所示，该簇放电模式为“Hopf/homoclinic”型簇放电。快子系统在 $\left(h_1,g_{{\text{CAN}}_{\text{Tot}1}}\right)$ 平面上的双参数分岔如图4(d)所示，同样的，全系统轨线在分岔曲线f和homo之间跃迁一次，对应于混合簇中的一个胞体簇。之后， $g_{{\text{CAN}}_{\text{Tot}1}}$ 的突然增加，使混合簇的胞体部分结束，进入树突部分。

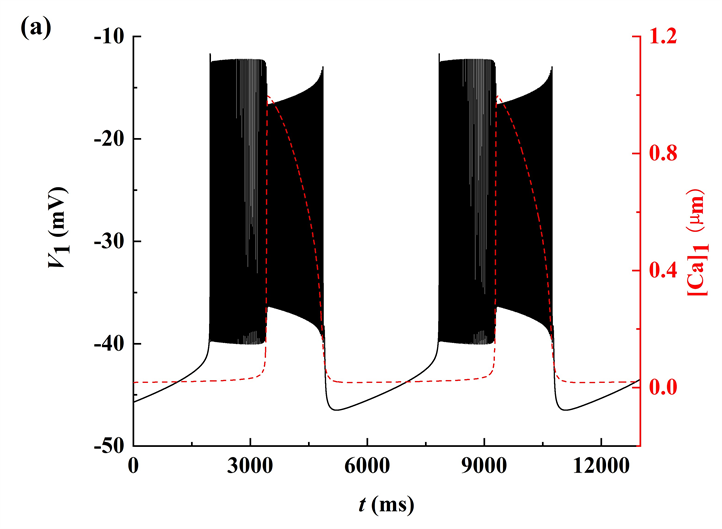
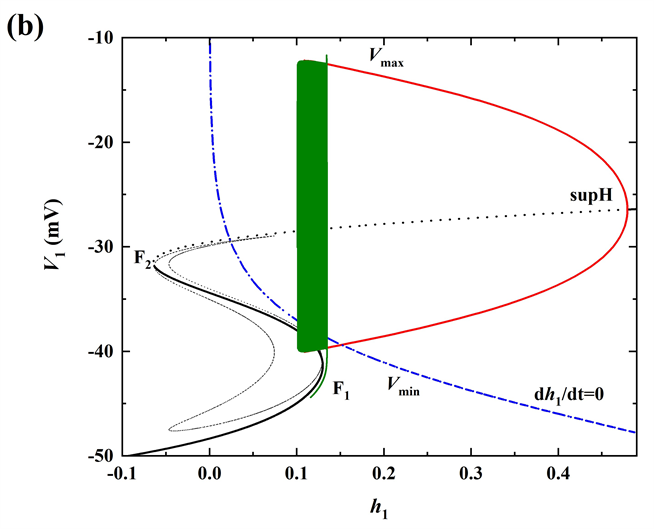
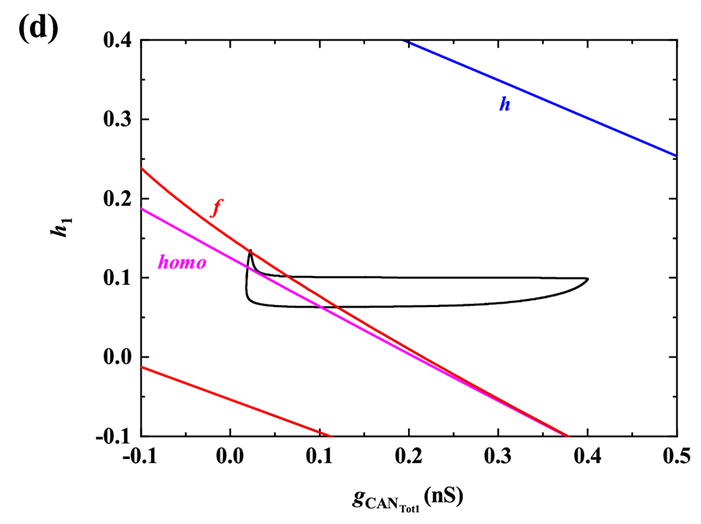
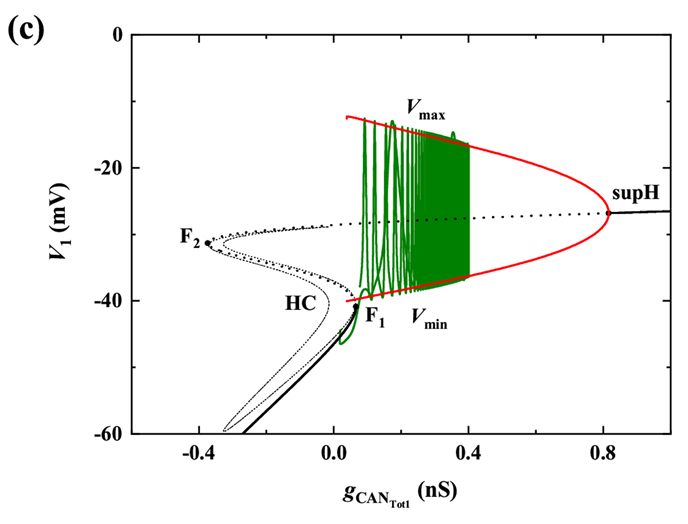
Figure 4. When $g_{\text{Na}}=5\text{nS}$ (a) Time series of membrane potential V₁ (black curve); (b) Bifurcation structure of the fast subsystem for the somatic bursting; (c) Bifurcation structure of the fast subsystem for the dendritic bursting; (d) Two-parameter bifurcation of the fast subsystem with respect to the slow variable $g_{{\text{CAN}}_{\text{Tot}1}}$ and h₁

图4. $g_{\text{Na}}=5\text{nS}$ 时 (a) 膜电位V₁ (黑色曲线)的时间序列；(b) 胞体簇的单参数分岔分析；(c) 树突簇的单参数分岔分析；(d) 簇放电的双参数( $h_1,g_{{\text{CAN}}_{\text{Tot}1}}$ )分岔分析

当g_Na继续增加至20 nS时，超临界Hopf分岔supH消失，亚临界Hopf分岔subH出现，同时不稳定极限环以及极限环的鞍结分岔LPC出现，且发生了稳定和不稳定极限环相遇的流分岔(TR)。此时，轨迹没有到达平衡点，如图5(d)所示，所以系统没有回到静息，而是出现长短峰的循环。

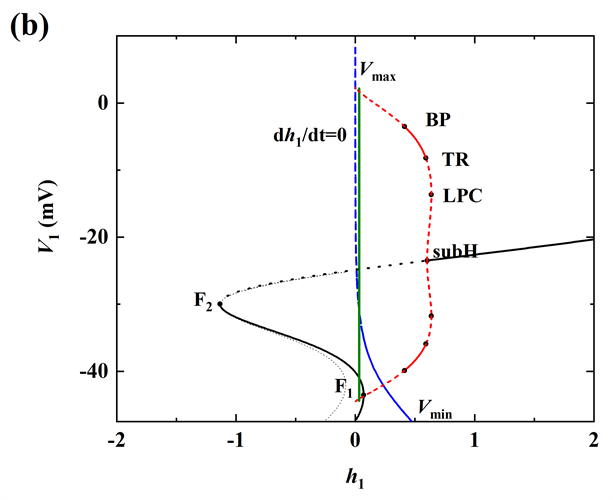
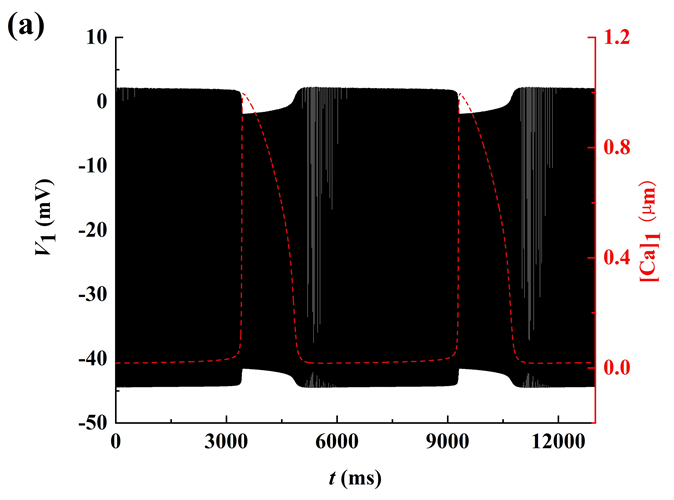
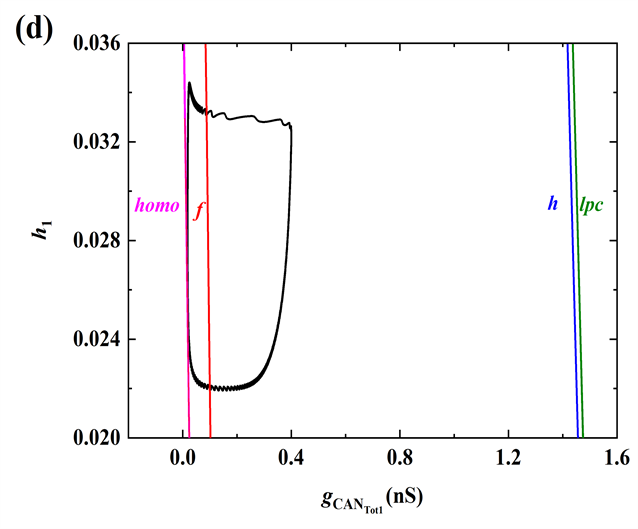
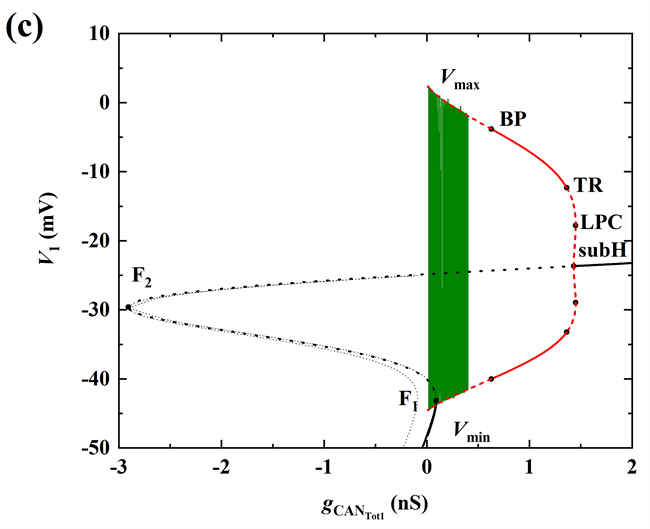
Figure 5. When $g_{\text{Na}}=20\text{nS}$ (a) Time series of membrane potential V₁ (black curve); (b) Bifurcation structure of the fast subsystem for the somatic bursting; (c) Bifurcation structure of the fast subsystem for the dendritic bursting; (d) Two-parameter bifurcation of the fast subsystem with respect to the slow variable $g_{{\text{CAN}}_{\text{Tot}1}}$ and h₁

图5. $g_{\text{Na}}=20\text{nS}$ 时 (a) 膜电位V₁（黑色曲线)的时间序列；(b) 胞体簇的单参数分岔分析；(c) 树突簇的单参数分岔分析；(d) 双参数( $h_1,g_{{\text{CAN}}_{\text{Tot}1}}$ )分岔分析

参数的微小变化一般不会引起系统很大的变化，但关键点附近的变化可能会引起系统的突变(如系统在周期与混沌之间的转换；簇放电模式的转变等)，而峰峰间期(ISI)是描述系统动态特性的一个状态变量。

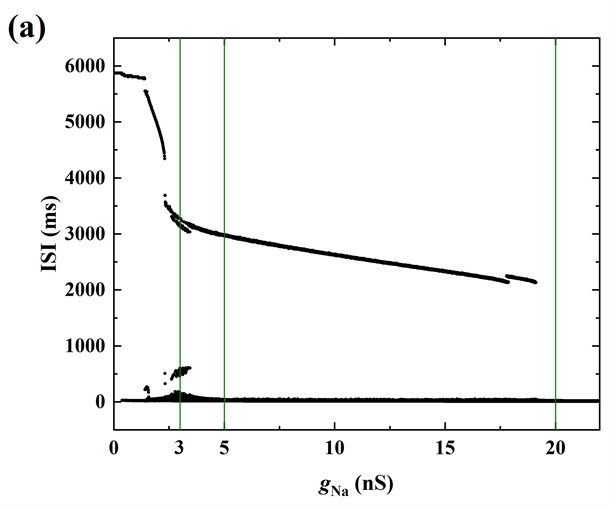
Figure 6. (a) The change of ISI sequence with g_Na; (b) After taking the logarithm of ISI sequence

图6. (a) g_Na变化时膜电位V₁对应的ISI序列；(b) 取对数后的ISI序列

为此，我们可以通过ISI分岔图进一步揭示g_Na对神经元电活动的影响，如图6(a)所示。簇放电(如 $g_{\text{Na}}=3$ 或5 nS时)由静息和反复放电两个状态构成且静息阶段对应ISI的最大值，但是峰放电没有静息阶段，故对峰放电(如 $g_{\text{Na}}=20\text{nS}$ 时)而言，ISI的最大值变小。这是簇放电与峰放电的另一个区别。

随着g_Na的增大，两簇之间由原来静息的状态逐步变为尖峰放电状态，相邻两个簇放电之间的间距逐渐变小，直至消失，即变为峰放电状态，对应最大ISI逐渐降低。图6(b)取对数后的ISI序列。

4. 结论

神经动力学的研究范围包括神经元的电生理学、神经传递物质的作用、神经网络的形成和塑性、神经退行性疾病的发生机制等。在神经科学领域中，神经动力学是一项非常重要的研究领域，对于理解神经系统的功能和疾病机制具有重要意义。

Pre-Bötzinger复合体在呼吸节律产生中至关重要，通过对病态节律的研究可以为相关疾病的治疗提供解决方向。本文主要研究了钠电导(g_Na)变化对耦合的pre-Bötzinger复合体中兴奋性神经元同相簇放电模式的影响，并从动力学角度揭示了不同类型的簇放电模式及其转迁机制。结果表明，g_Na的变化导致耦合pre-Bötzinger复合体中兴奋性神经元分别表现为树突簇、混合簇以及长短峰的循环三种放电模式。当g_Na增加时，超临界Hopf分岔supH消失，亚临界Hopf分岔subH出现，同时不稳定极限环以及极限环的鞍结分岔LPC出现，引起放电模式的转迁。因此，g_Na对耦合pre-Bötzinger复合体中兴奋性神经元的放电节律有重要的影响，也为进一步探索呼吸节律的产生机制提供了有价值的思考。

本文的研究有助于更好地理解pre-Bötzinger复合体呼吸神经元以及大脑其他区域的不规则簇放电，研究方法可以推广并应用于其他具有多时间尺度的神经系统的研究中。类似方法也可用于解释金融系统的稳定性、金融危机采取正确策略等 [23] 。

基金项目

本文得到郑州科技学院教师提升工程优秀青年教师(80000320018)资助。

NOTES

^*通讯作者。