基于指针数组的Gr?bner基方法的优化

Optimization of Gr?bner Basis Method Based on Pointer Array

摘要: 门级整数乘法器电路的验证是形式化验证领域内的一个难题，目前最有效的方法是Grӧbner基方法。在基于此方法的验证过程中，多项式的表示对内存的使用情况有很大的影响。在验证工具Teluma中，多项式表示为单项式的链表。由于链表结点需要同时存储数据元素本身的信息和一个指示其直接后继的信息，这会占用较大的内存空间。针对这一问题，本文对多项式的数据结构进行了优化，采用了动态数组存储单项式，指针数组表示多项式的方法。实验结果表明，该优化方法减少了验证过程中内存的使用。

Abstract: The verification of gate-level integer multiplier circuit is a difficult problem in the field of formal verification, and the most effective method is Grӧbner basis method. In the verification process based on this method, the representation of the polynomial has a great influence on the amount of memory used. In the verification tool Teluma, polynomials are represented as linked list of mono-mials. Because linked list nodes need to store both information about the data element itself and a message indicating its immediate successor, this takes up a large amount of memory space. To solve this problem, this paper optimizes the data structure of polynomials. Dynamic array is used to store monomials and pointer array is to represent polynomials. The experimental results show that the optimization method can reduce memory usage in the verification process.

1. 引言

形式化验证可用于推导给定电路相对于预定义规范的正确性 [1] 。为防止与奔腾浮点除错误类似的问题再次发生，算术电路的形式化验证是极其重要的。但到目前为止，算术电路，尤其是整数门级乘法器电路的形式化验证仍然是一个重大难题。

研究者们已经提出了几种用于乘法器的验证方法，包括可满足性(SAT)问题的方法 [2] 、判定图法 [3] 、定理证明器法 [4] 和代数法 [5] 。目前最有效的方法是代数法中的Gröbner基方法。将电路的所有逻辑门和规范用多项式表示，再使用多项式归约算法来检查这些多项式是否隐含了电路规范。但在验证过程中，多项式和冗余单项式的数量过多，严重影响了验证的速度 [6] [7] 。

为提高验证的速度，研究者们不断优化和改进Gröbner基方法。提出了XOR重写和Common重写 [8] 、逐位验证 [9] 和加法器重写 [10] 等方法，减少了冗余单项式的数量，简化了Gröbner基，缩短了验证的时间。但是，当乘法器的末级(FS)加法器为复杂的加法器时，仅应用Gröbner基方法很难验证。

在文献 [7] 中，复杂的FS加法器被简单的加法器所替换。结合SAT求解器能够验证等价性的特点，用SAT求解器验证了替换步骤的正确性，用Gröbner基方法验证了简化的乘法器。为节省加法器替换的时间，在文献 [11] 中，提出了在多项式编码中添加表示否定节点的对偶变量，并通过尾部替换和进位重写算法，简化了复杂的FS加法器，实现了验证工具Teluma。

工具Teluma中将多项式表示为单项式的链表。多项式的表示直接影响着多项式的生成效率和多项式所占用的内存空间，进而影响着Gröbner基方法的效率和验证过程中内存的使用。由于链表结点在存储数据元素本身的同时，还需要存储直接后继的存储位置，这使得占用的内存空间较大。

为减小多项式占用的内存空间，本文优化了Teluma中多项式的数据结构。使用动态数组存储单项式，将多项式表示为一个由指向Monomial数据类型的指针组成的指针数组。相比较于将多项式表示为单项式的链表，该方法节省了用于存储直接后继存储位置的内存。实验结果表明，该方法减少了内存的使用。

2. 理论基础

2.1. Grӧbner基理论

本节简单介绍了Grӧbner基理论的相关定义，其他的定理及其证明参考文献 [12] 。

定义2.1. 设I为 $R\left[X\right]$ 的非空子集，若 $\forall p,q\in I$ ： $p+q\in I$ 和 $\forall q\in R\left[X\right]$ ， $\forall p\in I$ ： $pq\in I$ 。则称I是多项式理想。

定义2.2. 设 $g_1,\cdots ,g_s\in R\left[X\right]$ ，若 $I=\left\{g_1{h}_1+g_2{h}_2+\cdots +g_s{h}_s|h_i\in R\left[X\right]\right\}$ ，则集合 $G=\left\{g_1,\cdots ,g_s\right\}\subseteq R\left[X\right]$ 被称为理想I的基。即I是由G生成的，记作 $I=\langle G\rangle$ 。

定义2.3. 若项集上有序关系 $\le$ ，则对于所有项 $\tau$ ， ${\sigma }_{\text{1}}$ ， ${\sigma }_{\text{2}}$ ，当 $\text{1}\le \tau$ 时，有 ${\sigma }_{\text{1}}\le {\sigma }_{\text{2}}\Rightarrow \tau {\sigma }_{\text{1}}\le \tau {\sigma }_{\text{2}}$ 。

定义2.4. 设 $G=\left\{g_1,\cdots ,g_s\right\}\subseteq R\left[X\right]$ 为 $I\subseteq R\left[X\right]$ 的基，若 $\forall h\in I$ ， $\exists g_i\in G$ ： $lm\left(g_i\right)|lm\left(h\right)$ 。则集合G称为理想I关于序关系 $\le$ 的一组Gröbner基。

Gröbner基理论为理想成员问题提供了决策过程。对于给定的 $h\in R\left[X\right]$ 和基 $G=\left\{g_1,\cdots ,g_s\right\}\subseteq R\left[X\right]$ ，判断h是否属于G生成的理想。如果 $\left\{g_1,\cdots ,g_s\right\}$ 是一组Gröbner基，那么这个问题可以用一个多元带余除法来解决。当且仅当h除以G的余数为零时，多项式 $h\in \langle G\rangle$ 。

对于上面应用的多项式环 $R\left[X\right]$ ，考虑本文的研究内容，我们使用D-Gröbner基的更一般的理论，其中系数环是一个主理想域(PID)。设D为PID，设P为理想 $I\subseteq D\left[X\right]$ 的基，若 $\forall q\in I$ ， $\exists p\in P$ ： $lm\left(p\right)|lm\left(q\right)$ 。则称集合P是理想I关于序关系 $\le$ 的一组D-Gröbner基 [7] 。本文中令 $D=Z$ 。

2.2. 代数模型

在应用Grӧbner基理论的代数推理中，电路需要使用多元多项式建模。在本文中，我们考虑门级无符号整数乘法器电路C，它具有2n个输入位 $a_0,\cdots ,a_{n-1},b_0,\cdots ,b_{n-1}$ ，2n个输出位 $s_0,\cdots ,s_{2n-1}$ ，以及内部AIG节点 $l_0,\cdots ,l_{k-1}$ ，所有变量均为布尔变量。

定义2.5. (字典项序)对于所有项 ${\sigma }_1=x_1^{d_1}\cdots x_r^{d_r}$ ， ${\sigma }_2=x_1^{e_1}\cdots x_r^{e_r}$ 。若 $\exists i$ ： $d_i<e_i$ ，对于所有 $j<i$ ： $d_j=e_j$ ，则有 ${\sigma }_1<{\sigma }_2$ 。

定义在字典项序下的变量为

$X=a_0,\cdots ,a_{n-1},b_0,\cdots ,b_{n-1},l_0,\cdots ,l_{k-1},s_0,\cdots ,s_{2n-1}$ (1)

将每个逻辑门的输出u与输入v，w之间的关系表示为布尔多项式，常见的多项式表示如下：

$\begin{array}{l}u=\neg v\iff -u+1-v=0\\ u=v\wedge w\iff -u+vw=0\\ u=v\vee w\iff -u+v+w-vw=0\\ u=v\oplus w\iff -u+v+w-2vw=0\end{array}$ (2)

我们称这些多项式为门多项式或门约束。设 $G\left(C\right)\subseteq Z\left[X\right]$ 为每个AIG节点对应的门多项式的集合， $G\left(C\right)$ 中的多项式都按字典项序排列，即每个节点的输出变量都大于其输入变量，这种排序也称为逆拓扑序。为了确保所有变量是布尔值0和1，我们为每个变量 $x\in X$ 加上关系式 $x\left(x-1\right)=0$ ，并称这些多项式为布尔值约束，它们的集合表示为 $B\left(X\right)$ ， $B\left(X\right)\subseteq Z\left[X\right]$ 。

定义2.6. 设C是一个电路，称 $G\left(C\right)\cup B\left(X\right)$ 为电路C的多项式集。由多项式集生成的理想记为 $J\left(C\right)$ ， $J\left(C\right)=\langle G\left(C\right)\cup B\left(X\right)\rangle \subseteq Z\left[X\right]$ 。

定理2.1. 设C是一个电路，根据定义2.4，在字典项序下， $G\left(C\right)\cup B\left(X\right)$ 是 $J\left(C\right)=\langle G\left(C\right)\cup B\left(X\right)\rangle$ 的一组D-Gröbner基。

定义2.7. 设C是一个电路，

$L=-{\displaystyle \underset{i=0}{\overset{2n-1}{\sum }}{2}^i{s}_i}+\left({\displaystyle \underset{i=0}{\overset{n-1}{\sum }}{2}^i{a}_i}\right)\left({\displaystyle \underset{i=0}{\overset{n-1}{\sum }}{2}^i{b}_i}\right)$ (3)

称L为规范多项式。若多项式 $L\in J\left(C\right)$ ，则C是一个乘法器电路。

电路的规范是输入和输出之间所期望的关系。判断电路正确性的方法是验证电路是否满足其规范。已知在逆拓扑序下，多项式集 $G\left(C\right)\cup B\left(X\right)$ 是理想 $J\left(C\right)$ 的一组D-Gröbner基。根据理想成员问题的方法，应用规范L除以多项式集 $G\left(C\right)\cup B\left(X\right)$ ，并检查结果是否为零。当结果为零时，电路是正确的。

2.3. 对偶变量

在以往的门多项式编码中，分别使用 $l_i$ 和 $1-l_i$ 对AIG节点和其否定进行编码。图1显示了输入为 $l_1$ 和 $l_2$ 时AIG节点 $l_3$ 、 $l_4$ 和 $l_5$ 的门多项式。可以看到，在子节点的符号为否定时，门多项式中单项式的个数会相应的变多。在多项式的运算过程中，运算时间是根据单项式的个数发生变化的。为了减少运算的时间，考虑引进对偶变量。对于每个内部门变量 $l_i$ ， $1\le i\le k$ ，引进变量 $f_i$ ，对 $l_i$ 的否定进行编码。其中 $f_i=1-l_i\in \left\{0,1\right\}$ ，我们称 $f_i$ 为 $l_i$ 的对偶变量，记作 $\text{dual}\left(l_i\right)=f_i$ 。

如图1所示，在引进对偶变量后，对于AIG节点 $l_5=\neg l_1\wedge \neg l_2$ ，可以用 $-l_5+f_1{f}_2$ 进行编码，这使得门多项式中单项式的个数从原来的5减小到了2。

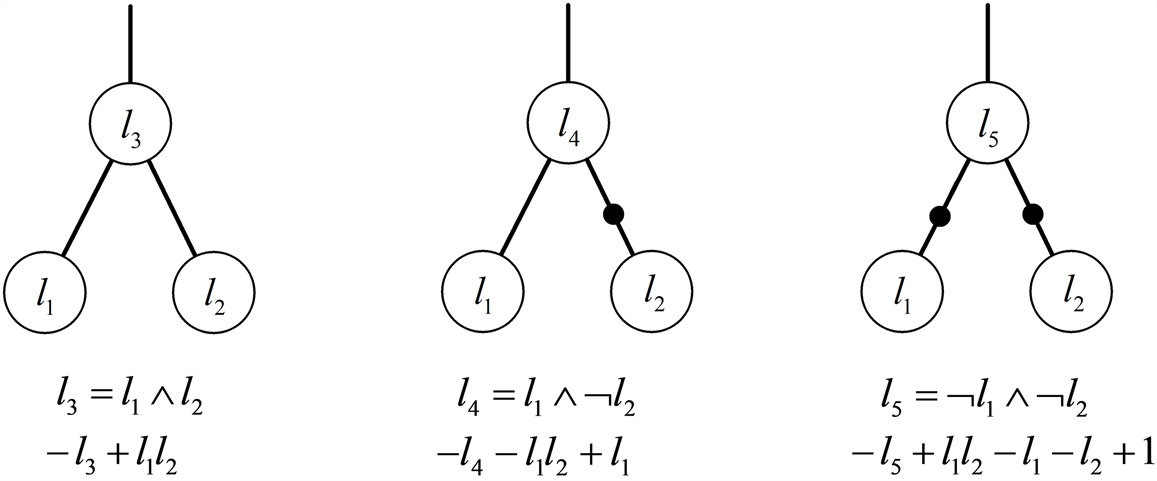
Figure 1. All polynomial encodings covered by AIG nodes

图1. AIG节点覆盖的多项式编码

定义2.8. 设 $D\left(C\right)=\left\{-f_i-l_i+1|l_i是C的一个内部\text{AIG}节点,f_i=\text{dual}\left(l_i\right)\right\}\subseteq Z\left[X\right]$ ， $G_D\left(C\right)\subseteq Z\left[X\right]$ 为添加对偶变量后的门约束集。电路C的多项式集生成的理想为 $J_D\left(C\right)=\langle G_D\left(C\right)\cup B\left(X\right)\cup D\left(C\right)\rangle \subseteq Z\left[X\right]$ ， $G_D\left(C\right)\cup B\left(X\right)\cup D\left(C\right)\subseteq Z\left[X\right]$ 中的多项式按逆拓扑序排列。对于每个门变量 $l_i$ ，有 $f_i>l_i$ 。

命题2.1. 设 $J_D\left(C\right)\subseteq Z\left[X\right]$ 如定义2.8所示，则 $G_D\left(C\right)\cup B\left(X\right)\cup D\left(C\right)$ 是 $J_D\left(C\right)$ 的D-Gröbner基。

在多项式编码中添加对偶变量后，通过进位重写技术简化复杂的FS加法器，再应用Gröbner基方法进行乘法器的验证。为实现含有对偶变量的验证工具，结合Amulet 2.0能够检测复杂的FS加法器及其组件等特点 [13] [14] ，添加基于尾部替换的进位重写算法，生成了Teluma工具 [11] 。

3. Grӧbner基方法优化

对于Gröbner基方法的优化，包括简化Gröbner基、加快Gröbner基的生成速度和减少内存的使用等方面。在应用工具Teluma的验证过程中涉及到了众多的数据结构，特别是单项式和多项式的表示。它们的表示影响着Gröbner基方法的应用效果，下面分别讨论它们的表示方法。

3.1. 单项式表示

单项式是由系数和项的乘积组成的代数式。在Monomial类的代码中，单项式表示为Monomial (mpz_t _c, Term * _t)，其参数分别表示系数和项。项是变量的幂次方的乘积，由于所有变量均表示布尔值，我们总是默认所有变量的指数均为1，即假设 $x\cdot x=x$ 。项可以表示为变量的有序链表，各变量的逻辑顺序通过链表结点的指针链接次序实现。项在归约过程中会被多次使用，因此把它们组织在一个动态放大的哈希表中。每次定义一个新项时，都需要计算它的哈希值并将其插入哈希表。同时使用参考计数器对项进行计数，计数器根据项在多项式中出现的频率递增和递减。

系数的值通常超过2⁶⁴，而C和C++语言既没有内建大数运算机制也没有对应的标准库实现。为了解决系数运算的问题，考虑使用GMP库进行数字表示，使用GMP库中的整数函数进行系数的运算。其中函数mpz_init_set(coeff, 1)，可将系数coeff赋值为1。例1以一个单项式为例，展示了它的表示形式。

例1. 对于单项式 $2l_1^2{l}_2{l}_3$ ，布尔变量 $l_1$ 的指数可自动减少到1。若变量 $l_1$ 、 $l_2$ 和 $l_3$ 的逻辑结构为 $\left(l_1,l_2,l_3\right)$ ，则它的链式存储结构如图2所示。

Figure 2. Representation of aterm

图2. 项的表示

其中 $\text{NULL}=^=0$ ，它表示最后一个结点的指针为“空”。设Monomial*m是一个指向单项式 $2l_1^2{l}_2{l}_3$ 的指针，应用 $\text{m}->\text{coeff}$ 即可知道该单项式的系数为2。

3.2. 多项式表示

在Teluma中，使用了std::deque将多项式存储为单项式的链表。但是根据容器deque的底层结构及链表结点的组成，在存储数据元素本身信息的同时还需要考虑直接后继存储位置的存储，这会占用较大的内存空间。针对这一问题，本文优化了多项式的数据结构。

多项式是有限个单项式的和。为构造多项式，单项式的存储是至关重要的。动态数组具有可动态分配内存的特点。考虑到事先并不清楚多项式中单项式的个数，选择使用动态数组存储用于构造多项式所需的单项式。随着不断将单项式添加到动态数组中，可逐步确定单项式的个数。数组元素全为指针变量的数组称为指针数组。相比较于链表，它仅需要考虑数据元素本身的存储。为减小多项式所占用的内存空间，在单项式的个数确定后，创建一个数组元素为指向Monomial数据类型的指针，长度与动态数组相同的指针数组，即应用该指针数组来表示多项式。在Polynomial类的代码中，多项式表示为Polynomial(Monomial**m, size_t len)，其参数分别表示单项式和单项式个数。对于该指针数组，内存大小为动态数组的长度和sizeof(Monomial*)的乘积。

下面以图1中AIG节点 $l_4$ 的门约束 $-l_4-l_1{l}_2+l_1$ 为例，讨论它的构造过程。首先分别构造输出和输入变量的多项式 $-l_4$ 、 $l_1$ 和 $1-l_2$ ，再根据与门的多项式表示进行多项式的乘法和加法运算。多项式的运算是对内部的单项式进行运算，再根据结果重新构造多项式。在最后的加法运算中，依次将三个单项式 $-l_4$ 、 $-l_1{l}_2$ 和 $l_1$ 添加到动态数组中，再应用相关函数即可构造出多项式 $-l_4-l_1{l}_2+l_1$ 。由于动态数组以2倍的方式扩容，所以表示该多项式的指针数组的长度应为4。例2展示了它的表示形式。

例2. 对于多项式 $-l_4-l_1{l}_2+l_1$ ，它是由3个单项式组成。根据上述的构造过程，该多项式可表示为一个长度为4的指针数组。具体的表示形式如图3所示。

Figure 3. Representation of polynomial

图3. 多项式的表示

其中 $\text{*mon}\left[\text{0}\right]=-l_{\text{4}}$ ， $\text{*mon}\left[\text{1}\right]=-l_1{l}_2$ ， $\text{*mon}\left[\text{2}\right]=l_1$ ， $\text{*mon}\left[\text{3}\right]=\text{0}$ 。

4. 实验

本次实验使用了一台带有Ubuntu20.04虚拟机的电脑，配备Intel(R) Core(TM) i5-11300H 3.10GHz CPU和16 GB主内存。实验所用时间以秒为单位，时间限制设置为300秒。实验代码及相关数据在文件experiments中。

首先，我们选择了AOKI基准集中 [15] 的192个64位无符号乘法器进行实验。其次，为分析优化前后该工具对于大型乘法器的验证情况，我们选择了由AristKojevnikov的脚本生成的简单乘法器进行实验，输入位宽分别为128位、256位和512位。实验结果如图4所示。

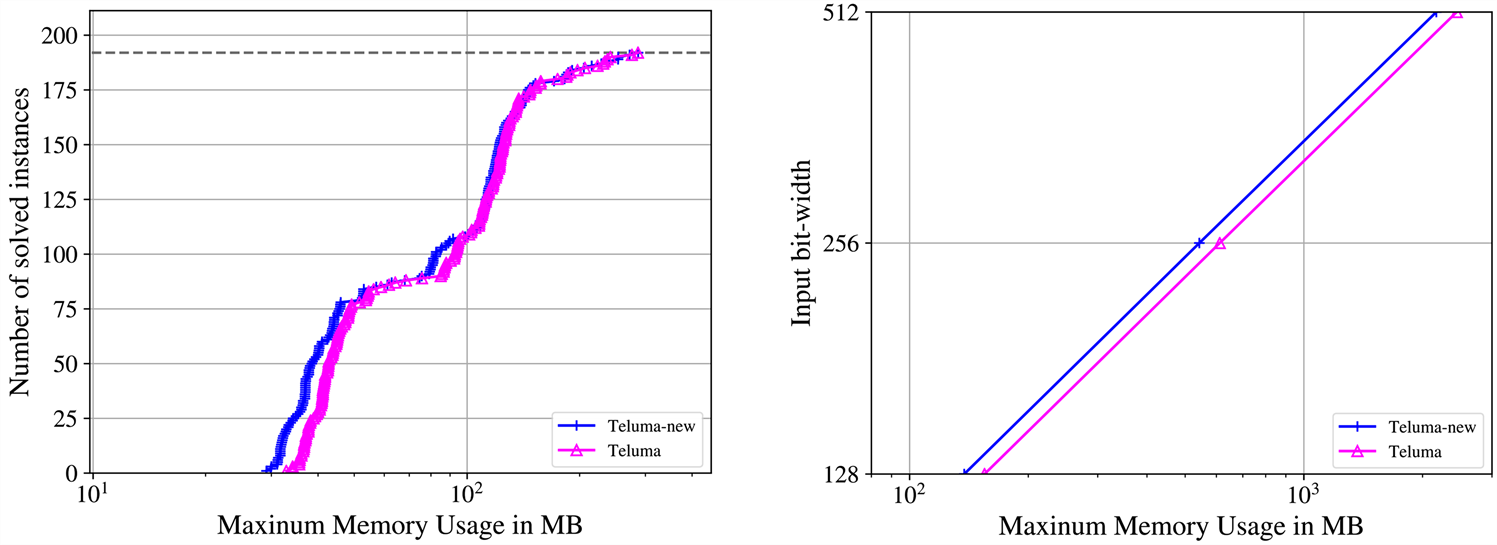
Figure 4. Maximum memory usage of AOKI benchmark set (left) and large multipliers (right)

图4. AOKI基准集(左)和大型乘法器(右)的最大内存使用情况

乘法器的验证过程并不一定是完全正确的，工具Teluma可以生成证明证书，用于检查验证过程的正确性。如果生成证明证书，会占用更大的内存空间。所以我们选取了AOKI基准集中的部分乘法器，用于分析在生成证明证书的情况下，优化多项式的数据结构对内存使用情况的影响。实验结果如表1所示。

Table 1. Comparative experimental data before and after optimization

表1. 优化前后对比实验数据

表1中显示的是在验证模式下，各类型乘法器的验证时间和占用的最大内存空间，其中默认生成的是统一的PAC证明格式的证书。通过查看图4的图像和表1的数据可以看出，该工具能够在给定时限内验证完成AOKI基准集和大型乘法器，并且在优化多项式的数据结构后，所占用的内存空间减小了。

5. 结论

本文优化了Teluma中多项式的数据结构，使用动态数组存储单项式，将多项式表示为由指向Monomial数据类型的指针组成的指针数组。实验结果表明，使用指针数组表示多项式的优化方法，能够减少验证过程中内存的使用。在未来的工作中，我们希望能够进一步确定添加了对偶变量的布尔多项式的最小表示。

NOTES

^*通讯作者。