基于Wohler曲线的车轮弯曲疲劳试验机关联性研究

Research on Correlation of Wheel Bending Fatigue Testing Machine Based on Wohler Curve

摘要: 因为两台不同生产厂家的汽车车轮弯曲试验机的控制系统和设备结构不同，即使设备的力传感器和转速传感器都校正一致，那么输出到车轮的弯矩值也会产生差异，从而对试验结果造成影响，这是车轮行业普遍存在的现象。那么为了验证两台不同生产厂家的汽车车轮弯曲试验机之间的差异到底有多大，并且找到设备之间的关联性尤为重要。首先在两台设备上分别测试10件车轮，通过设置相同的停机条件，得到两台设备停机时车轮的循环次数和裂纹位置，从而得出两台设备车轮循环次数的差异大小。然后使用同一批次的新车轮在裂纹容易产生的位置贴应变片，用同一个应变轮分别在两台设备上采集应变数据，从而得到两台设备之间的应变差异大小。最后引入伪损伤理论，基于雨流循环计数的概念，使用nCode软件计算出两台动态弯曲疲劳试验机的累积损伤结果，得到两台设备贴片位置的累积损伤差异大小，两台设备之间累积损伤的差异验证了车轮循环次数差异大小的准确性，并通过Wohler曲线公式推导出两台设备之间的关联转化关系。

Abstract: Because the control systems and equipment structures of two automobile wheel bending testing machines from different manufacturers are different, even if the force sensors and speed sensors of the equipment are calibrated consistently, the bending moment values output to the wheels will be different, thus affecting the test results, which is a common phenomenon in the wheel industry. So in order to verify the difference between two automobile wheel bending testing machines from dif-ferent manufacturers, it is particularly important to find the correlation between the equipment. Firstly, 10 wheels were tested on two equipments, and the cycle times and crack positions of the wheels when the two equipments stopped were obtained by setting the same shutdown conditions, thus the difference of the cycle times between the two equipments was obtained. Then, strain gauges are attached to the crack-prone positions with new wheels of the same batch, and strain data are collected on two devices with the same strain wheel, so as to obtain the strain difference be-tween the two devices. At last, based on the concept of rain flow cycle counting, the cumulative damage results of two dynamic bending fatigue testing machines were calculated by using nCode software, and the cumulative damage difference between the two devices was obtained. The cumu-lative damage difference between the two devices verified the accuracy of the difference in wheel cycle times, and the relationship between the two devices was deduced by Wohler curve formula.

1. 引言

车轮是汽车的重要零部件，承受着汽车行驶过程中的各种力和力矩，起着承载、转向、驱动、制动等作用，因此车轮直接影响汽车的安全性和可靠性 [1] 。汽车车轮最主要的失效形式是疲劳破坏，车轮的疲劳寿命是衡量车轮质量的最重要的指标。目前国内外车轮标准都规定了动态径向疲劳试验和动态弯曲疲劳试验，从大量试验结果来看，车轮因弯曲疲劳试验造成失效的比例比径向疲劳试验要高得多，因此弯曲疲劳试验是检验车轮疲劳寿命的最主要指标 [2] 。汽车车轮标准中要求了动态弯曲疲劳试验机结构形式和设备精度，但是经过试验发现，同一批次的车轮在两台不同的动态弯曲疲劳试验机上可能会得到不同试验结果。出现这种情况的原因有可能是车轮样件本身存在不同的缺陷，也有可能是设备间存在差异。车轮是被测的样品，只有找到设备之间的差异性才能更准确地评价车轮的安全性。本文通过比对两台不同生产厂家的动态弯曲疲劳试验机，并使用延展性好、弹性大、振幅大、试验周期短的钢制车轮作为比对样品，在消除外在试验影响因素下，更准确地对车轮样品结果和应变损伤结果进行分析比较。

随着实验室之间联系的加强，相互间的关联和比对会越来越频繁，这就需要通过有效的方法对试验机间的差异性进行检测 [3] ，通过金属材料疲劳理论，通过系数关联建立试验机之间结果一致性。

2. 车轮动态弯曲疲劳试验

2.1. 试验释义

车轮动态弯曲疲劳试验是模拟车辆在拐弯运动中汽车车轮持续承受弯矩和交变载荷情况的一种试验，用于测试其疲劳强度 [4] 。

2.2. 设备结构

目前，主要有两种车轮弯曲疲劳试验方法：

一种方法是让车轮进行旋转，而载荷固定不动，即车轮随着加载臂的旋转而旋转，在加载臂一端施加一个固定的弯矩，对车轮产生旋转弯矩。把车轮与疲劳试验机的工作台固定在一起，用电机来驱动疲劳试验机的工作台及与其固定在一起的车轮进行旋转运动，在加载臂的一侧连接上车轮的轮毂，而在加载臂的另一侧则施加一个固定不变的力，用来实现对加载臂即车轮轮轴产生一个旋转弯矩的效果，以便真实反映汽车车轮在行驶过程中承受旋转弯矩的实际状况。在模拟试验条件下，要求汽车车轮在经历了若干次循环载荷之后，不能产生由于疲劳所致的破坏。

另一种方法是让车轮静止不动，而载荷进行旋转，即车轮跟加载轴固定，在加载臂一端施加一个相当于旋转弯矩效果的离心力。把车轮与疲劳试验机的工作台台面进行绑定，与第一种方法一样，在加载臂的一侧连接上车轮的轮毂。与第一种方法不一样的是，在加载臂的另一侧则装载一个不平衡的质量块，通过电机带动装载的不平衡质量块进行转动，用来产生一个离心力，进而实现对加载臂即车轮轮轴产生一个旋转弯矩作用在汽车的车轮上 [5] 。

2.3. 试验弯矩

弯矩的确定：

按下式确定弯矩M (力 × 力臂)，单位为牛顿·米(N·m)：

$M=\left(\mu R+d\right)F_{v}S$ (1)

式中，M为轮胎与路面间的设定摩擦系数；R为轮胎静负荷半径，是汽车制造厂或车轮厂规定的用在该车轮厂规定的用在该车轮上的最大轮胎静半径，单位为米(m)；d为车轮内偏距或外偏距(内偏距为正值，外偏距为负值)，单位为米(m)；F_v为车轮或汽车制造厂规定的车轮上的最大垂直静负荷或车轮的额定负荷，单位为牛顿(N)；S为强化试验系数 [6] 。

2.4. 试验参数

每台机器测试10件车轮样品，所有样品设置好试验参数(见表1)，车轮加载弯矩值、试验转速、停机偏移量、以及螺栓紧固力矩并进行试验，保证试验中2台设备的所有试验车轮都可以按照统一试验参数进行。

Table 1. Test parameters

表1. 试验参数

2.5. 试验条件

按照车轮GB/GMW等标准要求，根据实验室车轮测试规程，设定好试验条件(见表2)，尽量使检测设备为单一变量。

Table 2. Test conditions

表2. 试验条件

2.6. 车轮样品

汽车车轮结构多种多样，本次试验使用辐板式钢制车轮，车轮规格6.5 J × 16，偏距40 mm，螺栓孔5 × ϕ14 mm。

2.7. 试验结果

2.7.1. 设备停机时循环次数

Table 3. Number of cycles during equipment shutdown

表3. 设备停机时循环次数

设备停机时循环次数(见表3)，设备A的10件样品平均值为44,890转，设备B的10件样品平均值为34,695转，相差10,195转，设备A的10件样品的平均值为设备B的10件样品平均值的129.0%，根据正态分布图(见图1、图2)可见两台动态弯曲疲劳试验机的试验结果存在明显差异。

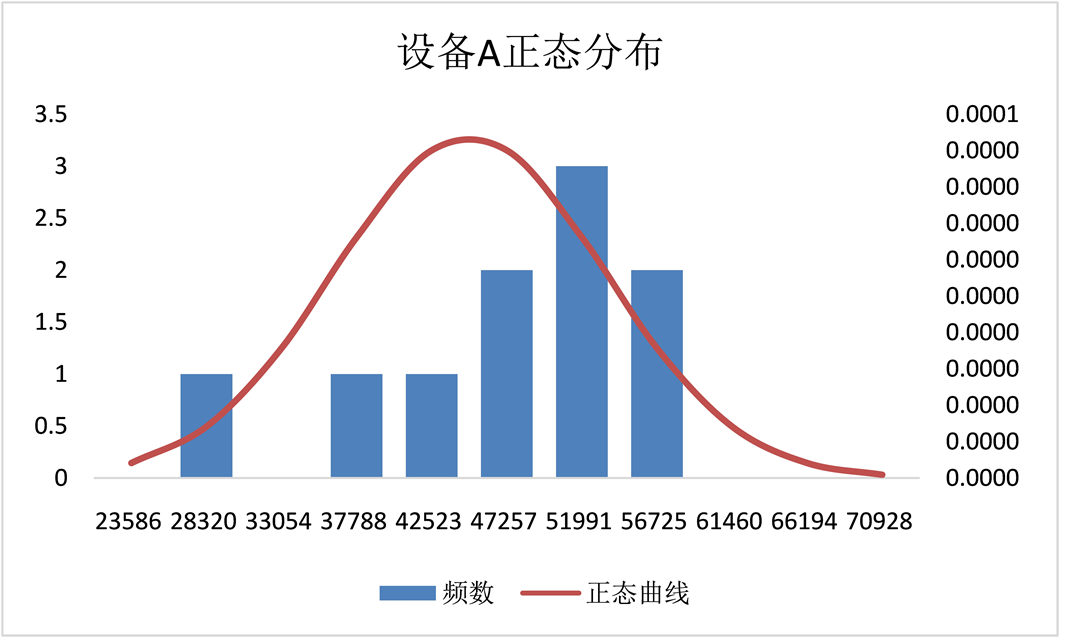
Figure 1. Normal distribution of number of cycles of the equipment A

图1. 设备A循环次数正态分布

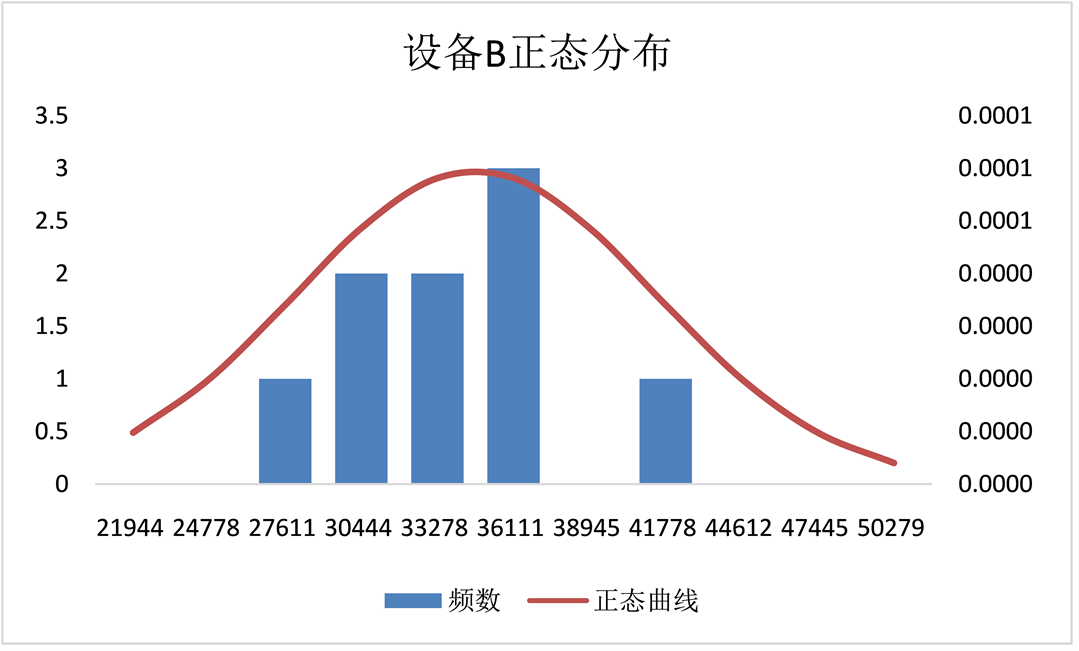
Figure 2. Normal distribution of number of cycles of the equipment B

图2. 设备B循环次数正态分布

2.7.2. 裂纹位置

20件样品的裂纹位置(见表4)，所有车轮在通风孔(见图3)和通风孔向螺栓孔方向20 mm圆周(见图4)位置都有裂纹产生。

Table 4. Crack location

表4. 裂纹位置

Figure 3. Cracks in ventilation holes after flaw detection

图3. 探伤后通风孔裂纹

Figure 4. Cracks in the middle position of the ventilation hole and the bolt hole after flaw detection

图4. 探伤后通风孔与螺栓孔中间位置裂纹

设备A：

50%的车轮在1#通风孔位置出现了裂纹；

50%的车轮在4#通风孔位置出现裂纹；

30%的车轮在13#通风孔位置出现裂纹；

30%的车轮在14#通风孔位置出现裂纹；

20%的车轮在15#通风孔位置出现裂纹；

设备B：

80%的车轮在1#通风孔位置出现了裂纹；

20%的车轮在4#通风孔位置出现裂纹；

30%的车轮在13#通风孔位置出现裂纹；

20%的车轮在15#通风孔位置出现裂纹；

说明两台动态弯曲疲劳试验机对样品产生的破坏形式大体相同。

3. 应变轮数据采集

3.1. 贴片位置

因为在通风孔和通风孔向螺栓孔方向20 mm圆周两个位置出现裂纹，将应变片贴在这两个裂纹位置，更能准确的反映出车轮在两台设备的受力情况，选择1#、4#、7#、10#、13#通风孔5个位置和车轮内侧通风孔向螺栓孔方向20 mm圆周2个180度对称的位置，一共7个贴片位置，对应位置编号为0、1、2、3、4、5、6。

3.2. 贴片方式

采取1/4桥式，应变片方向垂直于裂纹方向。

3.3. 应变采集周期

因为车轮的寿命周期短，在两台设备采集的时间过长，容易使车轮发生明显损伤，会导致两台设备的数据比较失真，所以不宜采集太长时间的应变数据，每件车轮采集2分钟，考虑两台设备分别10个车轮的停机循环转数不同，设备A的车轮平均停机转数较大，刚开始对车轮的损伤较小，先采集设备A，再采集设备B。

3.4. 应变数据分析

Table 5. Strain amplitude

表5. 应变幅值

两台设备的应变幅值(见表5)，设备A的应变幅值上限和幅值下限比设备B的应变幅值上限和幅值下限都要大，7个贴片位置的幅值上限平均数相差72，幅值下限平均数相差89，幅值平均数相差161，设备A与设备B的应变幅值平均数比例为104%，通道4时域统计图(见图5)，代表通风孔应变位置，通道5时域统计图(见图6)，代表通风孔向螺栓孔方向20 mm圆周应变位置。

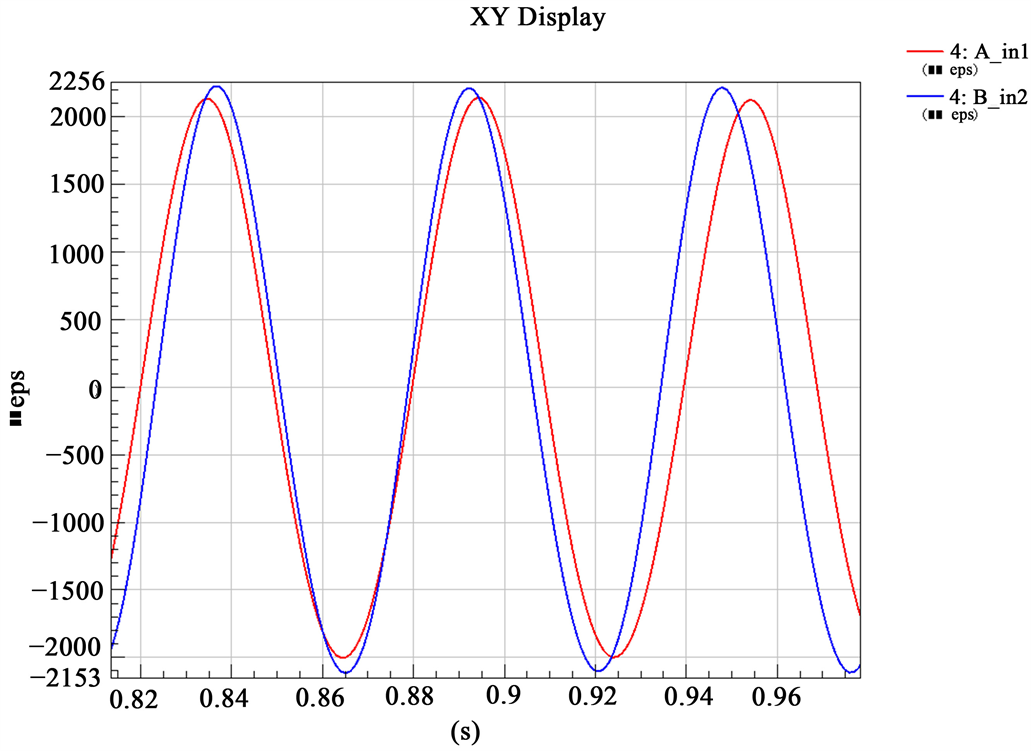
Figure 5. Channel 4 (vent location) time domain plot

图5. 通道4 (通风孔位置)时域图

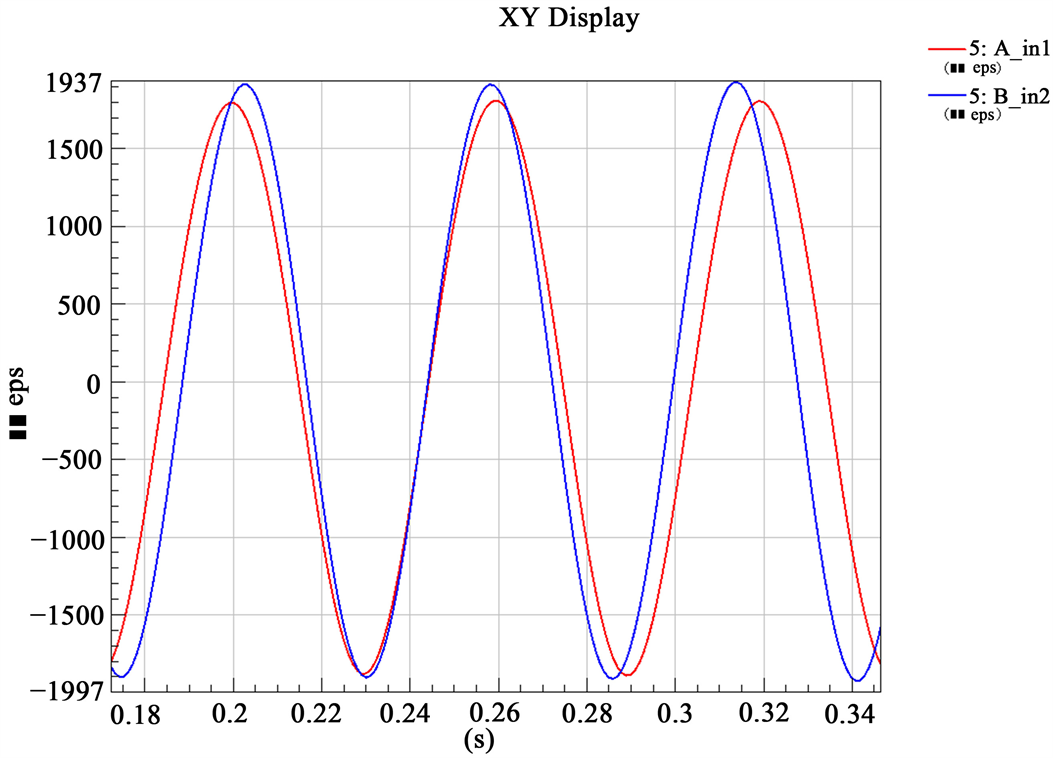
Figure 6. Channel 5 (middle of the vent hole and bolt hole) time domain diagram

图6. 通道5 (通风孔与螺栓孔中间位置)时域图

4. 设备差异性验证

4.1. 伪损伤计算

引入伪损伤理论，基于Wohler曲线、Palmgren-Miner准则和雨流循环计数的概念，输入载荷是一组雨流循环。最简单的Wohler曲线以Basquin方程的形式给出 [7] 。

$N=\alpha \cdot S^{-\beta }$ (2)

其中，幅值为S_i的循环损伤贡献是1/N_i，最简单的损伤累积准则是Palmgren-Miner准则，它对所有计数载荷的损伤求和。

$D={\displaystyle \underset{i}{\sum }\frac{1}{N_i}=\frac{1}{\alpha }}\cdot {\displaystyle \underset{i}{\sum }{S}_i^{\beta }}$ (3)

我们希望伪损伤不依赖于材料模型，因此将伪损伤数定义为：

$d={\displaystyle \underset{i}{\sum }{S}_i^{\beta }}$ (4)

式中，D为计数载荷的损伤求和；α为比列常数；S_i为应变幅值；β为损伤指数。

相比前式，该定义去掉了比例常数α，式中唯一的材料参数是损伤指数β，通常对于汽车零部件选取损伤指数β = 5。

因为被测车轮寿命周期较短，在所采集应变值中有应变变大的趋势，为减小误差，选取设备A的尾部数据和设备B的靠前数据，每个通道选取200个循环。使用nCode软件通过伪损伤公式计算得到两台动态弯曲疲劳试验机每个通道的累积损伤结果。

4.2. 损伤值比较

设备A与设备B的7个通道位置的应变损伤值比例在121.2%~136.7%之间，平均值为127.2% (见图7)。

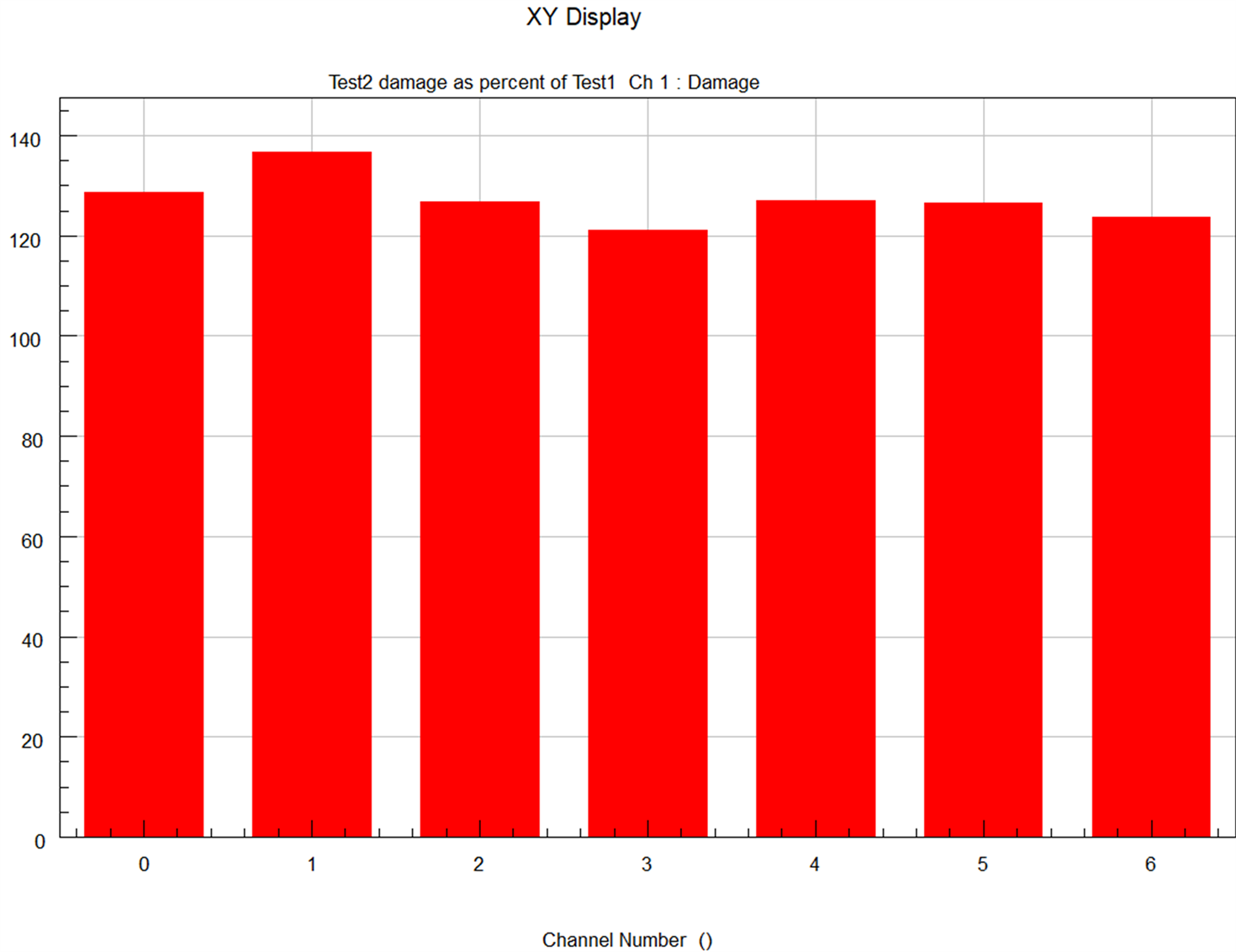
Figure 7. Damage scale plot of each channel of two equipments

图7. 两台设备各个通道的损伤比例图

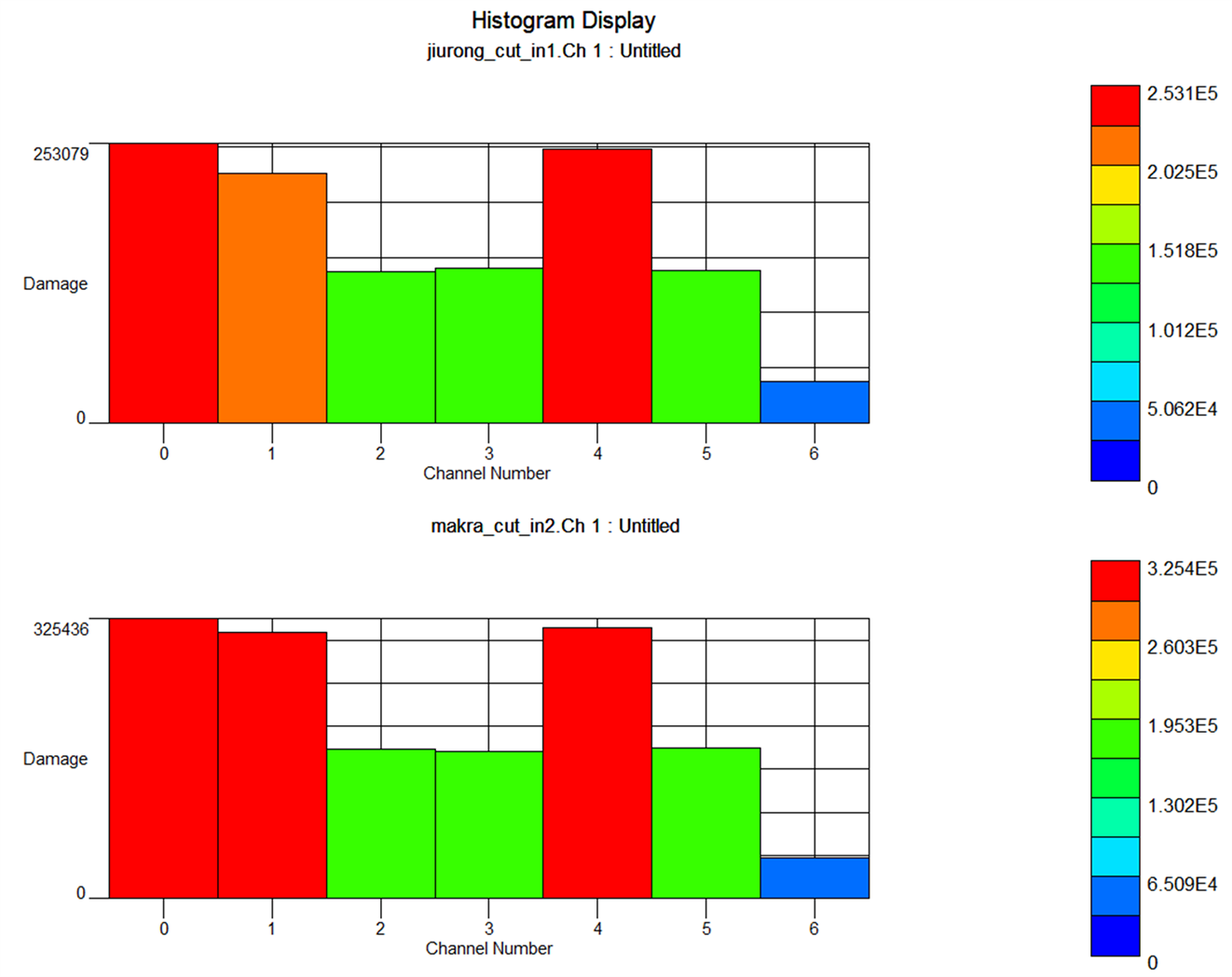
Figure 8. Cumulative damage values of strain in each channel of two equipments

图8. 两台设备各个通道的应变累积损伤值

4.3. 差异性验证

设备A与设备B在0号贴片位置损伤值最大，分别为325,436和253,079，两台设备均在0、1、4号应变位置的损伤值明显大于其他位置(见图8)，并且这三个位置刚好对应1#、4#、13#通风孔位置，也是裂纹出现频率最多的地方，与车轮的试验结果相符合。

设备A与设备B之间的损伤值比例关系为127.2%，设备A与设备B之间的循环次数比例关系为129.0%，损伤值之间的比例和循环次数之间的比例非常接近，验证了设备A和设备B分别做10件车轮的结果差异，那么对于此次试验的车轮，两台设备之间的差异为29%，可见两台设备之间的差异性还是很大的。

5. 设备的关联性

想要减小两台设备之间的差异，需要在两台设备之间建立关联，由于两台设备之间的损伤值比例关系和试验循环次数比例关系一致，那么根据Wohler曲线公式(5)推导出设备A和设备B之间函数关系(8)

$N=\{\begin{array}{l}\alpha S^{-\beta },S>S_{\text{f}}\hfill \\ \infty ,S\le S_{\text{f}}\hfill \end{array}$ (5)

式中，N为疲劳失效循环数；S为载荷的应力幅值；α为描述材料的疲劳强度，β为损伤指数；S_f为疲劳极限。

设备A和设备B的Wohler曲线公式：

$N_A=\alpha S_A^{-\beta },S_A>S_f$ (6)

$N_B=\alpha S_B^{-\beta },S_B>S_f$ (7)

假设设备A和设备B之间的校正系数为G，那么：

$N_A=G\times N_B$

推导出：

$G={\left(\frac{S_A^{-\beta }}{S_B^{-\beta }}\right)}^{-\beta }$ (8)

根据设备A与设备B的应变幅值平均数比例为104%，β = 5，得到G = 0.8219。

根据设备A的10件样品平均值为44,890转，那么N_A × G = 36,895转，与设备B的10件样品平均值为34,695转非常接近，说明校正系数G为设备A与设备B之间的关联转换系数。

6. 结论

1) 本文选用与试验车轮同一批次的车轮作为应变轮，在裂纹出现频率最多的地方测量应变，应变测量计算出的损伤累积数据与试验数据一致，并且两台设备均在0、1、4号应变位置的损伤值明显大于其他位置，这三个位置刚好对应1#、4#、13#通风孔位置，也是裂纹出现频率最多的地方，与车轮的试验结果相符合，两台设备之间累积损伤的差异验证了车轮循环次数差异大小的准确性，得到了基于此次试验车轮两台设备之间差异值。

2) 此文验证了两台不同生产厂家的汽车车轮弯曲试验机会得出不同的试验结果，因此，有必要确定一个基准试验台，对其他的参考试验台进行校正，由参考试验台的结果乘以校正系数G，得到与基准试验台非常接近的结果，减小了设备间的差异，达到设备的之间的标准统一，保证了车轮产品在测试准确性和安全性。