0~1规划模型在信用评分卡组合优化问题中的应用

The Application of 0~1 Programming Model of Credit Scorecard Combinatorial Optimization Problem

摘要: 针对信用评分卡组合优化问题，首先运用穷举法解出原问题，之后参照二次无约束二值优化模型与0~1规划模型，将信用评分卡组合问题转化成整数规划模型，利用python程序进行模拟求解不同组合不同阈值下的最终收益，并对结果进行讨论分析，得出最优的信用评分卡组合。

Abstract: For the credit scorecard combinatorial optimization problem, first using the exhaustive method to solve the original problem, and then refer to the quadratic unconstrained binary optimization model and 0~1 programming model to convert the credit scorecard combination problem into an integer programming model, and using the python program carry out simulation to solve the final income of different combinations and different thresholds, and discussing and analyzing the results to obtain the optimal combination of credit scorecards.

1. 引言

在银行信用卡或相关的贷款等业务中，需要先通过各种审核规则对客户的信用等级进行评定，通过评定后的客户才能获得信用或贷款资格。银行需要根据各种审核规则对客户的信用等级进行评定，这些规则就称为信用评分卡，每个信用评分卡又有多种阈值设置，这就使得不同的信用评分卡在不同的阈值下，对应不同的通过率和坏账率。因此，银行的目标是选择最合理的信用评分卡组合以及其阈值，使得银行最终收入最多。规则审核过程实际是经过一重或者多重组合规则后对客户进行打分，这些规则就被称为信用评分卡，每个信用评分卡又有多种阈值设置(但且只有一个阈值生效)，这就使得不同的信用评分卡在不同的阈值下，对应不同的通过率和坏账率，因为信用评分卡在现实中有广泛的作用，所以有越来越多的人来对此问题进行研究，如吴佳辉 [1] 利用特征处理的方法建立的评分模型，但是该模型只适用于特征比较少的情况；谢瑞 [2] 利用逻辑回归、随机森林等方法建立了评分模型，但该模型计算复杂度较高；高嘉，任亚明 [3] 利用模拟退火算法来建立优化模型，但该模型因遵守模拟退火算法的核心Metropolis准则导致在迭代末期，结果的出现的概率低，精确性不高；而国外的一些学者，如M.H.M.A. Jahromi [4] 等人利用0~1混合整数目标规划模型来解决机床选择和操作分配问题，但该模型方法非精确，不能得到全局最优解；Özgür Ülker [5] 等人利用0~1规划模型来解决办公室空间分配问题，但该模型约束条件过多且计算复杂；Khaled Alhamad [6] 等人利用非线性整数规划来建立模型解决预防性维护计划中的设备维护及水电分配问题，该模型以0~1规划为主，模型结果较优，符合实际情况，所以本文也利用了0~1规划模型进行建模。

我们由简单到复杂进行研究，我们先研究在我们所选的100张评分卡中选出一张卡的一个阈值，使我们最终受益最大的问题。对此问题，采用穷举法将附件中的100张评分卡的每一个阈值的数据进行代入计算，找到最终收益最大的一张卡的一个阈值。

进行讨论分析，之后，我们研究选定的3张评分卡的各自10个阈值进行组合的问题，最后我们考虑在100张信用评分卡中选出3张信用评分卡来进行组合，得到最大收益的问题。

2. 符号说明

符号说明见表1。

Table 1. Symbol description

表1. 符号说明

3. 最优信用评分卡组合问题研究

3.1. 一张评分卡的一个阈值的最大收益问题

表2为本文研究所运用的部分数据。

Table 2. Part of the scorecard data of 100 credit scorecards

表2. 100张信用评分卡中部分评分卡数据

在100个信用评分卡中找出1张及其对应阈值，使最终收入最多，所以我们只需要将每个阈值的通过率与坏账率带入到所建立的最终收益模型中，找到最优解，我们将其作为已知数据，作为0~1规划模型的验证，之后我们将1张信用评分卡的不同阈值最终收益模型转化为0~1规划模型，之后利用python程序进行求解：

首先，我们利用matlab进行穷举，先写出同一张信用评分卡的不同阈值的最终收益的模型：

$z=w\cdot t\cdot \left(s-s\cdot h-h\right)$

我们先假设利息收入率为5%，要贷款10,000元，这时我们的模型中，不知道的未知量就只剩两个了，一个是通过率t，另一个是坏账率h，按照每一张评分卡的不同阈值对应的不同的通过率和坏账率，我们在matlab中利用for循环将每一个阈值中的通过率和坏账率输入进去，算出最终收益，并将其比较，得到最高收益为卡49的阈值1。

但是这只是针对利息收入率为5%的收益模型的最优值，于是我们改变利息收入率，代回这个模型中，得出利息收入率在1%~10%之间的得到最优收益时所选择的信用评分卡的序号，如图1所示。

Figure 1. Optimal scorecard sequence numbers at different interest rates

图1. 不同利率下的最优评分卡序号

由图1可知：

$y=\{\begin{array}{cc}54& 0<x\le 0.0232\\ 4& 0.0232<x\le 0.0323\\ 49& x>0.0323\end{array}$

其中x是银行贷款利息收入率，y表示信用评分卡的编号，例如在银行贷款利息收入率小于2.32%的时候，银行选第54张信用评分卡的时候收益最高，当银行贷款利息收入率大于2.32%小于3.23%的时候，银行选择第4张信用评分卡的时候收益最高，当银行贷款利息收入率大于3.23%的时候，银行选择第49张信用评分卡的时候收益最高。

之后我们将这个一张信用评分卡的最终收益的模型转换成0~1规划模型。

首先我们需要将所建立的模型符合自变量只能取得0或1的限制，所以我们把是否选择这张信用评分卡的某个阈值作为自变量，选择该阈值，则变量值为1，否则值为0，这样我们就可以把模型变成如下形式：

$\begin{array}{l}\max f\left(x\right)={\displaystyle \underset{i=1}{\overset{10}{\sum }}{x}_i}{z}_i\\ \text{s}\text{.t}\text{.}{x}_i\in \left\{0,1\right\},{\displaystyle \underset{i=1}{\overset{10}{\sum }}{x}_i}=1\end{array}$

此时，这种形式还并没有符合0~1规划模型，因为0~1规划模型中可以转换成 $x^{\text{T}}Ax$ 的形式，找到矩阵A后可以代入计算，所以，我们为了得到 $A{x}^2$ ，我们需要将这个式子变为二次多项式，我们令 $x_i=x_i^2$ ，这样我们的模型就变成了二次模型，就可以利用0~1规划模型的求解算法进行求解，此时的A有一个特点因为本题中的每个阈值之间并无关系，所以此时的矩阵A没有自变量的交叉项（例为 $C{x}_1{x}_2$ ，C为常数），只是一个对角矩阵，只有对角线上有元素，形式如下：

$A=\left[\begin{array}{cccc}{z}_1& & & \\ & z_2& & \\ & & \ddots & \\ & & & z_{10}\end{array}\right]$

则利用python的Pulp库可以计算0~1规划模型的最优值，numpy库可以使对n维数组的处理更加便利，这样可以求解出得到最优解时，所选择的信用评分卡以及其对应的阈值。

经验证，模型得到的结果与穷举法得到的结果相同。

3.2. 固定三张评分卡的阈值组合的最大收益问题

在已经选定的3张信用评分卡中选择相应的阈值组合，使最终收入最多，让我们建立0~1规划模型并求解：

我们将3张评分卡的各自10个阈值进行组合，利用matlab穷举法程序，将数据代入我们所建立3张评分卡阈值组合的最终收益模型中进行计算，选出最终收益最大的阈值组合，并将此模型转换成0~1规划模型，再利用python程序进行求解。

首先我们利用matlab进行穷举，然后将三个信用评分卡阈值对应的通过率相乘、坏账率相加，放入matlab程序进行穷举：

假设贷款利息收入率为5%，贷款金额为10,000元，然后对选定的三张信用评分卡的各个阈值进行排列组合，通过将不同评分卡阈值对应通过率相乘得到总通过率，将坏账率相加得到总坏账率，我们在matlab中利用for循环将每一组阈值获得的总通过率和总坏账率输入进去，计算比较出最高收益及此时的评分卡阈值，通过使用matlab来遍历这1000组数据，找出其中收益最大的阈值组合，并且求出其最大值。

之后我们将这个一组信用评分卡的最终收益的模型转换成0~1规划模型。

首先我们需要将所建立的模型符合自变量只能取得0或1的限制，所以我们把是否选择这张信用评分卡的某个阈值作为自变量，选择该阈值，则变量值为1，否则值为0，这样我们就可以把模型变成如下形式：

$\begin{array}{l}\max f\left(x\right)={\displaystyle \underset{i=0}{\overset{999}{\sum }}{x}_i}{z}_i\\ \text{s}\text{.t}.x_i\in \left\{0,1\right\},{\displaystyle \underset{i=0}{\overset{999}{\sum }}{x}_i}=3\end{array}$

我们再将这个式子变为二次模型，就可以利用0~1规划模型的求解算法进行求解，而固定三张评分卡的三个阈值组合的最大收益问题中的每个阈值之间仍并无关系，所以此时的矩阵A也没有自变量的交叉项，只是一个对角矩阵，只有对角线上有元素：

$A=\left[\begin{array}{cccc}{z}_0& & & \\ & z_1& & \\ & & \ddots & \\ & & & z_{999}\end{array}\right]$

则利用python的Pulp库可以解决0~1规划问题，求解出得到最优解时，所选择的信用评分卡以及其对应的阈值。我们通过将选定三张信用评分卡的不同阈值进行重新组合，然后我们使用了一种新型定位方式来确定使用的信用评分卡对应的阈值，我们首先固定前两个信用评分卡的阈值，然后通过改变第三个信用评分卡的阈值来进行逐次遍历，即1000种组合，我们将其记为000到999。

经验证，模型得到的结果与穷举法得到的结果相同。

3.3. 三张评分卡的阈值组合的最大收益问题

从100张信用评分卡中任选取三张信用评分卡，并选择阈值组合，使得最终收入最多，让我们建立0~1规划模型并求解。

我们在固定三张评分卡的三个阈值组合的最大收益问题中的收益模型是依旧可以适用于此问题的，我们只需要利用程序将100个信用评分卡取3张的不同的阈值组合，并使用收益模型比较即可，然后利用python程序进行求解，得出最优解。

首先，我们还是利用matlab穷举法，将所有可能出现的3张卡的组合中3个不同阈值的组合进行穷举计算，比较出最优的阈值组合，而此题照比固定三张评分卡的三个阈值组合的最大收益问题中复杂的地方在于穷举时需要取3张信用评分卡作为组合，之后每一个组合进行10乘10乘10次共1000次运算，所以穷举法计算时间较长，结果整理如表3所示。

Table 3. The result of matlab exhaustive method

表3. matlab穷举法的结果

之后，我们本应该应用python程序在100张卡里取3张，并在3张卡中运用第二题的模型，相当于是利用三次循环，取出其中的通过率和坏账率，之后利用：

$t=t_1\cdot t_2\cdot \cdots \cdot t_n$

$h=\frac{1}{n}\left(h_1+h_2+\cdots +h_n\right)$

将此时的总通过率和总坏账率算出来，并放入第二题所建立的三张评分卡的不同阈值收益模型中计算收益。

但是，根据问题一的收益模型：

$z=w\cdot t\cdot \left(s-s\cdot h-h\right)$

我们固定了贷款金额w = 1,000,000，利息收益率s = 5%，由于要使z最大，将w与s代入，可得 $0.05t\left(1-21h\right)$ 最大时，z最大，那么我们推广到本题中的三个信用评分卡组合问题，这时

$t=t_1\cdot t_2\cdot t_3$

$h=\frac{1}{3}\left(h_1+h_2+h_3\right)$

我们在取一个表中最优值的时候，为了近似替代，将 $t_1,t_2,t_3$ 和 $h_1,h_2,h_3$ 均代替为此时阈值的t和h，只要求出每一张表中的能使 $0.05t\left(1-21h\right)$ 最大时的阈值即可，这样我们的每个表中只剩一个阈值，之后再根据2.2的模型将问题转化成0~1规划，之后利用类似于固定三张评分卡的三个阈值组合的最大收益问题中的python程序进行求解进行找到三个表中的三个阈值的组合即为最优解，结果整理如表4所示。

Table 4. Applying python to solve the maximum benefit problem of three scorecards

表4. 应用python求解三张评分卡组合的最大收益问题

经验证，穷举法与模型求得结果均为卡8阈值2、卡49阈值2、卡73阈值2，结果相同。

Table 5. The scorecard data of 3 credit scorecards

表5. 3张信用评分卡数据

我们列出卡8、49、73在不同阈值下的通过率和坏账率数据，如上表5所示，与其他卡对比发现，卡8、49、73的通过率高于大部分其他卡，坏账率低于大部分其他卡，如图2、图3所示。我们再应用3.2的模型进行验证，得到卡8阈值2、卡49阈值2、卡73阈值2为最优组合，根据实验，我们建立的模型相对于穷举法极大的提高了运行速度，且实验结果合理，符合实际情况且与实际结果相同。综上，最优信用评分卡组合为卡8阈值2、卡49阈值2、卡73阈值2。

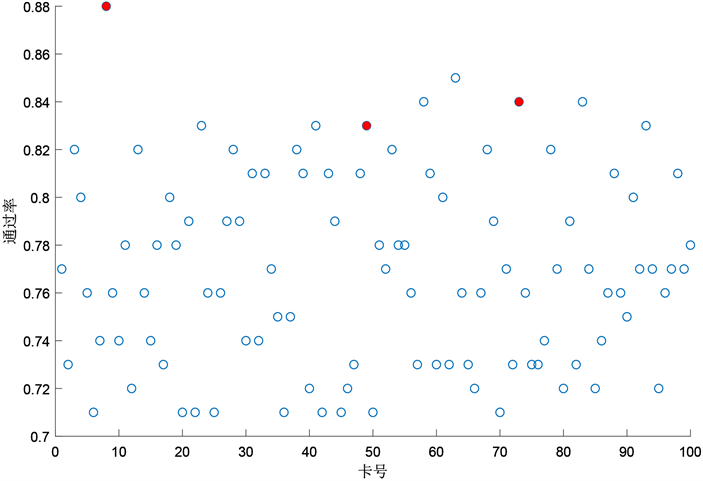
Figure 2. Comparison chart pass rates of all Scorecards when the threshold is 2

图2. 阈值为2时所有评分卡通过率对比图

Figure 3. Comparison chart of bad debt rates for all Scorecards when the threshold is 2

图3. 阈值为2时所有评分卡坏账率对比图

4. 模型评估

4.1. 模型的优缺点

模型的优点：

1、问题的难度由浅入深，建模思路也循序渐进，便于理解。

2、深入考虑了在利息改变情况下，最高收益的阈值组合会发生变化的情况，对于其他关于利息问题的研究具有一定的参考意义。

3、每一步得到的结果都与穷举法的精确结果作对照，经检验得到的结果相同，模型的用时更短。

4、模型的求解采用matlab软件与Python软件，得到的结果可信度较高。

模型的缺点：

1、现实生活中的银行利息大约在0.3%到5%之间，本题题目所设置的利息为5%，所以本文中的最优信用评分卡也会根据利息调整而不同。

2、现实生活中影响一个人的信用评分因素会更多，照比现实还有一定差距。

4.2. 模型的推广与改进

在问题分析中除了考虑现有的数据，还应该考虑其他与信用相关的数据，这样反映出的结果更合理，也更适合应用于实际。在模型建立时还可以使用最近提出的QUBO模型等新模型进行优化，从而降低程序运行的时长。