1. 引言
随着现代科技的飞速发展,在许多科学领域多样本高维数据以前所未有的速度不断产生,如基因DNA序列研究和生物医学成像等。在这些情况下,收集到的数据的特征数量通常超过样本量,这对经典统计学理论提出了根本挑战。因此,许多学者在对数据均值的研究中提出了新方法。
当样本总体只有两个时, [1] 最先指出Hotelling T2检验的不足,并提出了一种基于迹关系的渐进正态统计量。 [2] 推广上述方法构造出适合检验两样本Behrens-Fisher问题的u统计量,但是它们对非对角矩阵很敏感, [3] 又将空间符号检验的思想融入其中。 [4] 则提出了一种加权的双样本检验,选择恰当权矩阵实现统计量的渐近正态性去解决异方差问题。当存在两个以上样本组时, [5] 提出了基于著名Scheffe变换的L2范数统计量。 [6] 将 [2] 的双样本检验方法推广到多样本4阶矩有限的椭球分布情形, [7] 也将[2]推广到多样本异方差情形,并给出渐进方差的合理估计。 [8] 利用阈值化和数据变换证明了精度矩阵估计对检测边界的影响,提出了一种针对稀疏信号的强大检验。 [9] 研究了双向MANOVA问题并推广到更广泛假设下, [10] 在广义线性模型下,提出一种混合卡方近似的检验统计量。
上述测试均在高维空间上直接构造检验统计量,且在特定场景下非常强大,但大部分不能充分利用相关性信息,对协方差的迹施加各种限制。基于投影的测试是一类有效融合相关信息和降维的方法。 [11] 提出了一种随机投影程序,旨在在低维空间中使用Hotelling T2检验。 [12] 发现在尖协方差模型中,最优投影空间是主子空间的正交补空间,基于不同阶给出相应的渐进统计量。 [13] 证明投影平均技术可以定义一个稳健的双样本均值检验。 [14] 采用岭估计法将自适应投影思想应用于Hotelling T2检验,并推导出基于功率最优的一维投影方向。 [15] 提出了一种投影加权符号检验来解决高维检验问题,得益于使用样本分裂思想和一个正权函数,它能够显著控制第一类错误概率。 [16] 提出一种高维响应线性模型中回归系数矩阵的投影检验方法,并给出投影矩阵最优维数的上界。
本文的其余部分结构如下:在第2节中,我们利用Scheffe变换构造新样本组,利用投影矩阵在低维空间中进行参数的显著性检验,并提出检验统计量及其渐近分布;在第3节中,我们通过模拟试验确定检验中参数的取值并验证所提检验方法在不同设置下的第一类和第二类错误概率;最后一节对文章进行总结和讨论。
2. 多总体异方差数据的显著性检验
在本章中,我们提出了一种正态假设下的多总体异方差数据均值向量是否相等的检验方法。首先,利用Scheffe变换,将原始数据拉直成新向量,利用权重函数和空间符号函数抵消部分效率损失;通过投影矩阵投影到低维空间下构造检验统计量并推导出渐近分布,最后利用数值模拟的方法说明提出方法的优越性。
2.1. 模型构建
我们考虑以下问题:假设一共有
组p维独立样本,
,
,
,
,不失一般性有
。每组样本的协方差矩阵不要求相等,检验它们的均值是否相等,即
(1)
记
为第i组样本的前m个观测的均值,因此
是
的一个无偏估计。考虑著名的Scheffe变换:
(2)
本质上它将两个总体提炼成一个新总体,在正态假设下有优良的性质。随后我们拉直向量
(3)
其中
。这个方法利用每组的前
个样本信息,易证
之间是独立同正态分布的且
,
其中
则目标转换一个多重比较问题,检验新的均值参数是否为0。虽然转换要耗费一定时间,但单样本问题更方便建模。
[17] 提出了一种空间符号函数
,其中
来自一个p维标准正态分布,且它在部分非正态分布假设下也有较好表现。不难求得
,
,它的模只与维度高低有关,另外与方向向量独立。这要求我们构造一个满足
的
阶满秩矩阵
,利用SVD分解我们可以得到其中一个代数解
。早先检验在高维情形不适应的一种表现是第一类错误概率远小于显著性水平,为控制该误差我们引入一个正的权函数
,它能在
成立时不容易接受原假设。记投影样本
,此时维度p远大于
。我们考虑投影思想将样本投到低维空间再检验,设矩阵
与投影样本独立,其中l是一个较小的正整数,则(1)可改为
。 (4)
假设(4)与假设(1)虽不完全等价,但在势最大化的框架下寻找最优投影矩阵可以极大减少误差。基于(2)与(3)的结论,构造以下检验变量:
,
其中
。当下列假设成立时,
渐进服从自由度为1的卡方分布,当计算值大于上
分位点时我们不接受原假设。
假设1:当
趋近无穷时,
,
,
,
。
假设2:当维度足够大时,
存在,其中
。
假设3:存在一个特定的正数M,对任意常数
,权函数满足
当变量
充分大时。
假设1是多样本检验的必备条件,它确保每组样本大小不会差距太大,而且强调每组前
个样本也不会有太多信息损失,我们不在此讨论超高维情形。假设2保证高阶泰勒展开的有效性,即使它会变成1的高阶无穷小量,它大约是
的同阶无穷小量。权函数在“大p小n”情形下可以显著提高检验效率,许多函数满足该条件,例如幂函数、指数函数等。我们的检验对协方差的要求十分宽松,不需要低相关性假设。
基于以上假设,我们可以得到当
时
有最大势,而且投影方向是“oracle”最优投影方向。
2.2. 检验统计量
注意到拉直向量维度远大于样本量,在估计逆矩阵的时候受 [14] 启发,采用岭估计
,其中S为样本协方差矩阵,
为S中对角元素构成的矩阵,
为调节参数。
越大则估计越接近对角矩阵,且样本量越大则
应越小,此时估计
。
在模型构建中投影矩阵与
相等是才最有优势,这与假设两者独立冲突。 [18] 提出一种类似交叉验证的样本分割方法,记分割参数
表示分割比例,利用
样本寻找投影方向,剩余样本构造检验统计量(
表示四舍五入变换)。我们将投影样本数据集随机分成
和
,仅利用
中的信息完成全数据集的中心标准化,这样能保证
中的样本依旧能保证独立同分布,并获得投影方向的估计
,其中
。所有参数该取何值将在3.1节研究。则检验统计量为
, (5)
此时
。由于逐个变量估计产生的累积误差效应,导致检验统计量的方差远远大于理论值,不再是渐进
分布。利用上述结论和中心极限定理,将(5)式修正为
,
其中
是低维空间下样本方差的无偏估计,因此
也是渐进
分布,所有模拟均基于该统计量。
最后,基于建模过程可以将它推广到混合正态分布(一种椭球分布):
,它的密度函数可以写为
,其中
是一个多元正态分布的密度函数。除了混合正态分布,得益于一系列控制显著性水平的技巧,发现它在独立组件模型下也有较好表现。该模型可写为:
,其中
是一个正定矩阵,
满足均值为0,方差为p阶单位矩阵,所以每一个组件
是相互独立的。当
的四阶矩和
的最大和最小特征值均为有限非0值时,我们的检验统计量仍然有效。
3. 仿真模拟
在本节中,我们将通过蒙特卡罗模拟研究提出检验的性能。设置名义显著性水平为0.05,所有模拟结果均来自于100个独立重复实验取平均。在第3.1节中,构建模拟设置并基于最优势讨论不同分割参数和调节参数的影响,并给出了建议取值;在第3.2节中,在不同设置下研究了我们的方法和一个知名检验之间的I类误差和II类误差比较,并从正态分布推广到其他分布。
3.1. 试验设置及确定参数
简单起见,我们设定一共有3组数据。首先假定
,
和
均为0向量,
前100维均为v,其余元素均为0,显然
就能模拟第一类错误。对于协方差矩阵,考虑以下三种情况:独立结构
、自相关结构
和复合对称结构
,其中第二种和第三种类型蕴含变量相关性的信息,在本小节中取
为0.4、0.5、0.6分别对应
、
、
的结构。先考虑分割参数,此时依据经验固定调节参数
,利用网格搜索在[0.1, 0.9]的范围内每隔0.05取一次值,画出图像见图1。
由上图可知,不论v取0.1还是0.2,大体趋势一样,但在右图两侧相同间隔内势的变化幅度相对更大。不同的
值对势的影响较大,最大值集中在区间(0.4, 0.6)内,所有的曲线都近似一种凸对称的函数形式。某些异常点存在一些小波动是可能是模拟误差造成的,故不必在意。考虑到两部分集合的作用,我们更希望构造出来的检验统计量准确些,即
中含有较多样本,所以取
。
随后考虑调节参数的选择,令
,其中
,因为假定
与
呈负相关关系。其余设置均与分割参数相同,得到图2。我们发现每条曲线的波动都是相对温和的,没有明显的变化趋势,在独立结构下甚至为一条直线,与图1截然不同。因此
取任意值都可以,本文设置
。
基于以上结论再进行模拟比较,记新检验统计量为T1, [7] 提出的推广异方差统计量为TH。我们设定参数组合
为(200, 50, 70, 100)和(400, 100, 120, 150)。在局部备则假设下,固定
,此时
中有25%或50%的元素非0,可以看成稠密信号下的检验。情形①~③的设定同上文作为正态假设下的对比;情形④和情形⑤来自混合正态,取
,协方差设置同①和③;情形⑥中
来自
,情形⑦中来自
,选取公共
,
,
。随着维度的不断增加,变量的相关性也会增加。
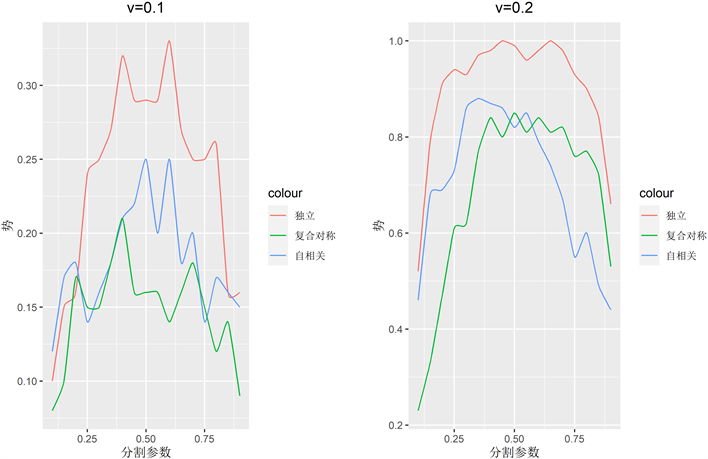
Figure 1. Power functions under different values of splitting parameter
图1. 不同分割参数取值下的势函数

Figure 2. Power functions under different values of tau
图2. 不同tau值下的势函数
3.2. 试验结果及分析
我们将情形①~⑦下的不同方法的I类错误和II类错误结果收录在表1中,

Table 1. Empirical size and power comparison of T1 and TH under different settings
表1. 不同设置下T1和TH的经验检验水平和势的比较
400
由上表可知在正态分布情况下,两种方法都接近名义显著性水平,在变量独立或者有低相关性,TH较好但T1也能接近TH的检验效率,在高相关性下TH效率损失严重。在混合正态分布中,两个方法都有一定效率损失,且在低维下TH的检验水平甚至达到0.14,其余结论类似,在高相关性下T1表现良好。在独立组件模型中,虽然在低维卡方分布组件下T1检验效果只有0.37,但其他模拟效果大致可以。左右表格对比,虽然高维下只有25%的非0元素,但检验效率更高,这可能是与Scheffe变换密切相关,较大的样本量可以保证更准确地估计出均值向量,从而统计量更加拟合卡方1分布。综上所述,新提出的拥有更广泛的适用场景,但当协方差矩阵为单位矩阵或相关信息有限时,如情形①、②和④下,建议不要使用投影方法降维,因为所有信息都是不可忽略的。
4. 总结和讨论
在本文中,我们提出了一种适用于有不同协方差矩阵的高维多样本的均值检验。数值结果表明,对于高相关性条件和部分非正态分布假设,新方法的效率优于现有的一些方法,而在低相关结构和正态假设下,新方法的性能与TH方法接近。我们主要关注的是维度和样本量以同阶速率趋于无穷,当以指数速率发散计算成本过高,而且第一类错误难以控制。未来可能的扩展是在统计量中加入一个纠偏项,从而抵消部分超高维数据带来的估计误差。样本分割策略虽然简单好用,由第三节的分析可知构造统计量的样本仅一半多一点,另外也有一些文章采用遍历寻找投影方向,但大幅增加了计算成本,到目前仍无其他更有效方法去处理投影问题。
致谢
作者感谢主编、编委会和匿名审稿人提出许多宝贵意见,这些意见促进文章有重大改进。作者对撰写文章时提供帮助的师生表示感谢。