基于FPGA和Sinc插值的分数阶傅里叶变换建模与设计

Modeling and Design of Fractional Fourier Transform Based on FPGA and Sinc Interpolation

摘要: 分数阶傅里叶变换(FrFT)在信号和图像处理领域受到了广泛的关注。在FrFT离散形式的演变过程中，低计算复杂度对实际应用至关重要。提出了一种高效的现场可编程门阵列(FPGA)实现FrFT算法的方法。本文将FrFT的计算过程分解为一次卷积和两次乘法的同时，为了提高插值精度，采用了sinc插值作为插值算法，并采用有限脉冲响应滤波器组成卷积模块，提高了信号卷积的鲁棒性。针对FPGA器件XC7VX690T，采用simulink和verilog硬件描述语言(HDL)对所提出的体系结构进行了综合。所得结果与仿真结果非常接近。最后，讨论了体系结构设计和硬件要求以及体系结构中的组成模块。

Abstract: Fractional Fourier transform (FrFT) has received much attention in the field of signal and image processing. In the evolution of discrete forms of FrFT, low computational complexity is essential for practical applications. An efficient method of implementing FrFT algorithm using field programma-ble gate array (FPGA) is presented. In this paper, the calculation process of FRFT is decomposed into one convolution and two multiplications. At the same time, in order to improve the interpolation accuracy, sinc interpolation is used as the interpolation algorithm, and the convolution module is composed of finite impulse response filter, which improves the robustness of signal convolution. For FPGA device (XC7VX690T), simulink and verilog hardware description language (HDL) were used to analyze the proposed architecture. The obtained results are very close to the simulation results. Fi-nally, the architecture design and hardware requirements as well as the components of the archi-tecture are discussed.

1. 引言

分数阶傅里叶变换(FrFT)作为传统傅里叶变换(FT) [1] 的推广，在低可观测机动目标检测 [2] 、彩色图像密码系统 [3] 、异常检测 [4] 、射频干扰抑制 [5] 、变分模态分解 [6] 、高光谱图像检测 [7] 等众多应用中已经成为一种新兴的数学工具。FrFT通过可选变换的分数阶(旋转角度)引入了额外的自由度，这在任何实际应用中都是对普通FT的改进。在信号处理领域，啁啾信号以其高范围分辨率和良好的抗干扰性能得到了广泛的应用。啁啾信号在时域和空域上都不紧凑。在时域和频域很难分离信号和噪声，因此我们可以在适当的分数阶傅里叶域中提取信号。FrFT有很多在啁啾信号处理中的应用，如宽范围啁啾速率测量 [8] 、啁啾信号抗干扰 [9] 、雷达成像 [10] 、时频分析 [11] 。

关于离散分数阶傅里叶变换(DFrFT)的演变，与离散傅里叶变换(DFT)不同，DFrFT有很多定义，所有可用的算法分为3类：发明的采样型 [12] 、加权求和型 [13] 和特征向量分解型 [14] 。采样式将连续FrFT计算信号离散化，并将其转化为乘法信号与啁啾信号的卷积形式。然后，通过信号乘法处理得到FrFT的结果。特征向量分解类型通过取DFT核矩阵的特征值和特征向量来构造DFT核矩阵的分数阶幂来计算DFrFT。特征向量分解可以保证FrFT的大部分特性，但其计算复杂度较高，不利于实时处理。加权求和型是指对任意特定角度的DFrFT进行加权求和即可计算任意角度的DFrFT，其计算精度与连续变换相比存在较大误差。

在FRFT理论提出后，基于现场可编程门阵列(FPGA)的FRFT实现很少。文献 [15] 完成了基于特征向量的DFrFT，文献 [16] 提出了基于多速率信号处理理论和滤波器组的FrFT计算算法的多相实现，文献 [17] 实现了加权求和型DFrFT。论文基于采样型实现通常采用双倍采样率来实现二次插值，并采用快速傅立叶变换(FFT)和快速反傅立叶变换(IFFT)在频域实现卷积。

本文主要研究了离散连续计算过程的采样型方法来完成DFrFT。讨论了啁啾信号在分数阶域的聚集特性，利用频域变换完成特定调频信号的识别。提出了一种资源利用率高、计算速度快、结果精度高的插补和卷积算法的FPGA实现方法。与文献 [16] 中的采样型实现不同，采用了有限脉冲响应(FIR)滤波器的sinc插值和时域卷积，提高了计算的精度，保证了数据的完整性。最后对系统的资源消耗进行了分析，证明了设计的适用性。

2. FrFT的基本原理

2.1. 连续FrFT

FrFT是一种参数搜索算法。传统的傅立叶变换是分析和处理平稳信号的一种标准而有力的工具，但在处理和分析时变非平稳信号时却显得较弱。FrFT可以理解为，当坐标轴在时频平面上绕原点逆时针旋转任意角度后，信号在分数阶傅立叶域中的表示。分数阶傅里叶变换提供了信号从时域到频域全过程的综合描述,随着阶数从0连续增长到1，分数阶傅里叶变换展示出信号从时域逐步变化到频域的所有变化特征。频响傅立叶变换是信号在一组正交啁啾基上的展开式，啁啾信号的某一阶的频响傅立叶变换也是一个脉冲函数。旋转角为α的信号 $x\left(t\right)$ 连续FrFT可以写成如下公式(1)的形式：

$X_a\left(u\right)=F^a\left[x\left(t\right)\right]\left(u\right)={\displaystyle {\int }_{-\infty }^{+\infty }{K}_a\left(u,t\right)x\left(t\right)\text{d}t}$ (1)

其中 $X_a\left(u\right)$ 是信号 $x\left(t\right)$ 变换的结果，P为变换的阶数， $K_a\left(u,t\right)$ 是变换的核函数，其定义为如公式(2)所示：

$K_a\left(u,t\right)=\{\begin{array}{c}{A}_a{\text{e}}^{j\pi (u^2\cot a-2ut\csc a+t^2\cot a)}\\ \delta \left(u-t\right)\\ \delta \left(u+t\right)\end{array}\begin{array}{c}a\ne n\pi \\ a=2n\pi \\ a=\left(2n+1\right)\pi \end{array}$ (2)

在这个内核函数中， $A_a=\sqrt{1-j\cot a}$ ， $P=2a/\pi$ 表示输入信号 $x\left(t\right)$ 的FrFT变换阶数，根据上述公式可知，当a = 0，P = 0时，变换后的结果为信号本身。当a = π，P = 2时，变换后的结果是信号的反转，即为 $x\left(-t\right)$ 。当 $a=\pi /2$ ，P = 1时，变换结果等价于 $x\left(t\right)$ 傅里叶变换。当 $a=3\pi /2$ ，P = 3时，变换结果等价于 $x\left(t\right)$ 傅里叶反变换。

FrFT处理以旋转角a为搜索参数的信号，其搜索周期为2π，由于 $a=P\pi /2$ ，故P阶的搜索周期为4。由于FrFT阶P的可加性 [12] ，当P为[0, 4]时，FrFT具有周期性。即为0 < P < 0.5，F^P为 $F^P{}^{+1}$ 的快速傅里叶逆变换；1.5 < P < 2时，F^P是 $F^P{}^{-1}$ 的快速傅里叶变换；P > 2时，F^P是 $F^P{}^{-2}$ 的反转。根据上述分析，可知将P可以限制在区间[0.5, 1.5]之间。

2.2. 啁啾信号的FrFT聚合特性

啁啾是信号的频率随时间变化的现象，是在时域上对脉冲性质做的一个表征，在一个脉冲周期内各频率成分不是同时到达的，就是激光脉冲的不同频率成分在时域上是不同步的，它分为正啁啾和负啁啾，正啁啾是频率随时间增加，就是激光输出先是低频再是高频，比如一个脉冲上升的前沿是低频，下降的后沿是高频，负啁啾反之。比如正常色散，高频波的折射率大，传播速度慢，而低频波的传播速度快，就形成正啁啾。啁啾产生的原因主要是由于介质的折射率由于动态电信号调制的影响产生动态变化，从而引起在介质中传播的光信号的相位发生变化，这种相位的变化直接体现为输出光信号频率的动态变化。

定义啁啾信号的表达式为公式(3)所示：

$x\left(t\right)={\text{e}}^{j\left(2\pi f_{o}t+\pi k{t}^2\right)}$ (3)

则根据分数阶傅里叶变换原理可得，啁啾信号的FrFT结果如公式(4)所示：

$X_a\left(u\right)=\sqrt{1-j\cot a}{\text{e}}^{j\pi u^2\cot a}{\displaystyle {\int }_{-\infty }^{+\infty }{\text{e}}^{j\pi t^2\left(\cot a+k\right)}}{\text{e}}^{j2\pi t\left(f_0-u\csc a\right)}\text{d}t$ (4)

假设公式(4)中的信号持续时间为 $\left[-\frac{T}{2},\frac{T}{2}\right]$ ，则公式能够表示为如下形式：

$X_a\left(u\right)=T{A}_a{\text{e}}^{j\pi u^2\cot a}\sin c\left[\pi T\left(f_0-u\csc a\right)\right]$ (5)

信号的啁啾率k = 3.91 × 10¹² Hz/s，信号带宽B = 20 MHz，中心频率f₀ = 0 Hz。当啁啾信号的旋转角度达到 $a=-\mathrm{arccot}k$ 时，其中k为信号的啁啾率，FrFT的结果变成sinc函数的形式，该sinc函数在 $u=f_0/\csc a$ 时达到最大值，同时在分数阶域中振幅值最大，说明在信号检测中，FrFT对chirp信号有聚集作用。

2.3. 离散FrFT

为了便于离散化操作，将连续FrFT表达式转换为公式(6)所示：

$X_a\left(u\right)=A_a{\text{e}}^{-j\pi u^2\tan \left(\frac{a}{2}\right)}{\displaystyle {\int }_{-\infty }^{+\infty }x\left(t\right){\text{e}}^{-j\pi t^2\tan \left(\frac{a}{2}\right)}}{\text{e}}^{-j\pi \csc a{\left(u-t\right)}^2}\text{d}t$ (6)

其中 $A_a=\frac{{\text{e}}^{-j\pi \mathrm{sgn}(\sin a)/4+ja/2}}{\sqrt{\left|\sin a\right|}}$ ， $a=P\pi /2$ ，由此可知，FrFT过程可以分解为以下三个计算过程：

1) 首先利用一个啁啾函数乘以要检测的信号，将这个啁啾信号命名为chirpA，这个信号的表达式为： $x_{\text{chirpA}}\left(t\right)={\text{e}}^{-j\pi t^2\tan \left(\frac{a}{2}\right)}$ ；

2) 将相乘后的信号与chirpB进行卷积，其中chirpB表达式为： $x_{\text{chirpB}}\left(t\right)={\text{e}}^{-j\pi t^2\csc a}$ ；

3) 将信号卷积乘以另一个啁啾信号chirpC，其表达式为 $x_{\text{chirpC}}\left(t\right)=A_a{\text{e}}^{-j\pi u^2\tan \left(\frac{a}{2}\right)}$ 。

经过量纲归一化处理后，每次采样计算的结果都可以与实际应用中离散信号的采样率和采样时间联系起来。设输入信号的持续时间为 $\left[-\frac{T}{2},\frac{T}{2}\right]$ ，T为时间宽度。信号的频域为 $\left[-\frac{f_s}{2},\frac{f_s}{2}\right]$ ，其中f_s为信号的采样率。维度归一化 [18] 是将不同维度的时域和频域转换为一维的同一域，引入具有时间维度的尺度因子S，并定义新的尺度坐标。根据时域和频域的区间长度计算，为使两个区间相等，则尺度因子S为 $\sqrt{\frac{T}{f_s}}$ ，则归一化宽度∆为 $\sqrt{T{f}_s}$ 。

在所有时间或频率标签中，函数可以被限制在区间 $\left[-\frac{\Delta }{2},\frac{\Delta }{2}\right]$ 内，这意味着Wigner分布被限制在围绕时频域原点的半径∆/2的圆内。啁啾乘法和啁啾卷积的Wigner分布将被紧凑地包含在一个半径为∆ [19] 的圆中。则区间变为 $\left[-\Delta ,\Delta \right]$ ，采样间隔为1/2∆。因为需要对原始输入信号进行双插值。最终离散FrFT表达式为：

$X_a\left(\frac{k}{2\Delta }\right)\approx \frac{A_a}{2\Delta }{\text{e}}^{-j\pi \tan \left(\frac{a}{2}\right){\left(\frac{k}{2\Delta }\right)}^2}{\displaystyle \underset{t=0}{\overset{N-1}{\sum }}{\text{e}}^{j\pi {\left(\frac{k-l}{2\Delta }\right)}^2\csc a}{\text{e}}^{-j\pi {\left(\frac{l}{2\Delta }\right)}^2\tan \left(\frac{a}{2}\right)x\left(\frac{l}{2\Delta }\right)}}$ (7)

公式中N代表采样点个数， $u=\frac{k}{2\Delta }$ ， $t=\frac{l}{2\Delta }$ 。

经FrFT后，输入信号 $x\left(t\right)$ 变为 $X_{\alpha }\left(u\right)$ ，在分数场的 $\left(P,u\right)$ 平面上有一个峰值点 $\left({\hat{P}}_0,{\hat{u}}_0\right)$ ，其中P为信号旋转阶数，u为分数场的幅值。从峰值点可以估计出信号的调频斜率 ${\hat{k}}_0$ 和中心频率 ${\hat{f}}_0$ ，表示为公式(8)所示：

$\{\begin{array}{c}{\hat{k}}_0=-\cot \left(\frac{\pi {\hat{P}}_0}{2}\right)\\ {\hat{f}}_0={\hat{u}}_0\csc \left(\frac{\pi {\hat{P}}_0}{2}\right)\end{array}$ (8)

经过尺度归一化的离散处理后，离散信号的实值可计算为公式(9)所示：

$\{\begin{array}{l}{k}_0={\hat{k}}_0{f}_s/T\hfill \\ f_0={\hat{f}}_0\sqrt{f_s/T}\hfill \end{array}$ (9)

3. FPGA实现与设计

3.1. DFrFT架构设计

本文所提出的体系结构的顶层框图如图1所示。这些模块共同完成了根据chirp速率计算最佳旋转角度，并通过最佳旋转角度获得所需的3个chirp信号，通过sinc插值将信号翻倍，完成对信号的乘法和卷积等4个主要操作。

Figure 1. Top-level block diagram of DFrFT architecture

图1. DFrFT架构的顶层框图

输入信号分为实部信号和虚部信号，同样，输出信号也分为实部和虚部。由于FPGA不支持复数计算，所以复数的乘法运算需要分别计算实部和虚部。一般来说，乘法模块需要四个乘法器，但通过结合类似的术语和其他操作，乘法模块可以简化为三个乘法器和一个额外的加法和减法，可以减少DSP的消耗。产生chirp信号的块根据公式(8)和公式(9)的输入信号的chirp率，在分数阶域中获得振幅最大的最佳旋转角度。由于chirpA和chirpC在形式上的相似性，这两个信号在FPGA实现中可以共享一个ROM，从而减少了资源占用。

3.2. Sinc插值和卷积块

Sinc插值算法，又叫香农插值算法(whittaker-shannon interpolation formula)，是一种用于从离散实信号构造时间连续带限函数的方法。是信号处理中一种非常常用、好用的插值补间算法，广泛并非常适合应用于多数振动信号及图形信号的拟合。在基于数字卷积的信号重采样方法中，从理论上讲，sinc插值是最好的方法之一，因为它不会扭曲由其样本定义的信号 [20] 。离散sinc插值最常用的实现方法是“信号频谱零填充法” [21] 。对于插值点f的sinc插值函数能够表示成如下形式：

$y\left(x\right)={\displaystyle \underset{k=0}{\overset{N-1}{\sum }}f\left(x_k\right)}\sin c\left(2\Delta \left(x-x_k\right)\right)$ (10)

其中 $\left\{x_k=\frac{k}{2\Delta }:k=0,\cdots ,N-1\right\}$ ，因此，它可以通过信号与sinc函数的卷积来计算，如果信号的长度为n，则需要O (NlogN)的运算。sinc插值模块的FPGA实现结构如图2所示。

Figure 2. Sinc interpolation block

图2. Sinc插值块

在上述架构中，我们使用FIR滤波器 [22] ， [23] 来完成卷积运算。与FFT和IFFT实现频域卷积的方法相比，FIR滤波器具有更快的计算速度和更简单的结构，同时避免了FFT在FPGA实现过程中丢失数据的问题。将sinc函数作为系数存储到FIR滤波器中，然后对分离出来的复信号进行滤波，就可以完成对输入信号的二次插值。

与插值块类似，卷积块中的卷积也是以FIR滤波器为核心，不同的是卷积块的两个输入都是复数。因此，我们在插值块中需要四个FIR滤波器。在所提出的体系结构中，许多计算和结构具有相似性和可重复性，例如啁啾信号的计算和卷积的计算，这说明了所提出体系结构的简单性和易于实现性。

4. 仿真结果及资源分析

在本节中，本文给出了一个实现N = 256点FrFT的FPGA实现，信号的参数如下：信号的啁啾率k = 3.91 × 1012 Hz/s，信号带宽B = 20 MHz，中心频率f₀ = 0 Hz。最优阶P可由式(8)和式(9)求得，可计算出该信号的最优阶P约为1.06。然后我们可以通过图1中的架构完成FrFT的FPGA实现。针对vertex-7 FPGA器件(XC7VX690T)，采用verilog HDL对所提出的设计进行了综合和实现。

图3和图4是不同P值的matlab仿真结果。图5和图6是数据量化后在simulink中FPGA实现的结果。通过simulink仿真得到的结果与MATLAB仿真得到的结果基本一致，证明本文所提出的架构在FPGA上实现的可行性与有效性。

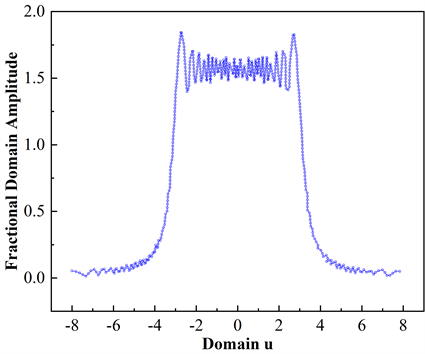
Figure 3. FrFT waveform diagram of 256-Point chirped signal with P = 0.80 in MATLAB

图3. MATLAB中对P = 0.80的256-Point啁啾信号的FrFT波形图

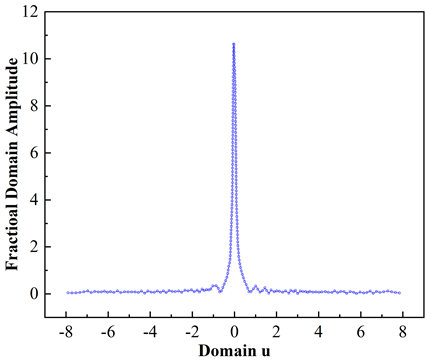
Figure 4. Frequency response analysis of 256-Point chirped signal with P = 1.06 in MATLAB

图4. MATLAB中对P = 1.06的256-Point啁啾信号频响分析

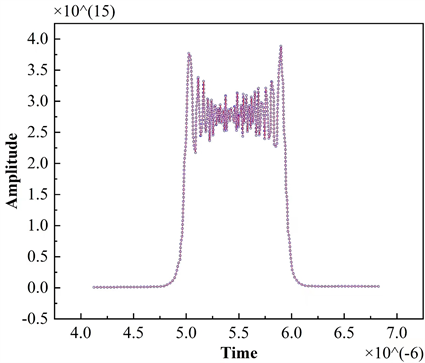
Figure 5. The frequency response Fourier transform result of the signal realized in FPGA using the proposed architecture is P = 0.80

图5. FPGA中使用所提出的架构实现的信号的频响傅立叶变换结果为P = 0.80

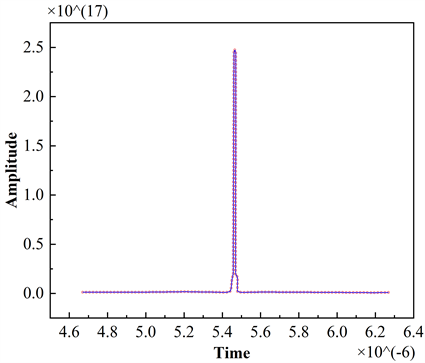
Figure 6. FRFT results at P = 1.06 for the signal implemented in FPGA using the proposed architecture

图6. 在FPGA中使用所提出的架构实现的信号在P = 1.06处FRFT结果

实现中BRAM、DSP、LUT、寄存器等FPGA资源利用率如表1所示。从表中的数据可以看出，在这样的硬件平台上，资源的使用处于较低的水平，说明了所提出的架构的实用性。

与文献 [17] 完成128点DFrFT的结果相比，ram、lut和dsp的比例有所降低。该结构的运行时间为2.819 µs，比文献 [16] 和文献 [17] 的运行时间要快，说明本文所提出的架构的科学性以及有效性。

Table 1. Resource utilization rate

表1. 资源利用率

5. 总结

本文提出了一种计算DFrFT的有效硬件体系结构。利用simulink对该体系结构进行了仿真描述，并在目标FPGA器件上进行了综合和实现。并将实现结果与信号在理想情况下MATLAB中的仿真结果进行了比较，simulink实际波形的验证与MATLAB中理想波形基本一致，验证本文提出架构的科学性与有效性。实验结果表明，该设计能够在低功耗的情况下实现高精度。因此，该体系结构能够满足实时性的要求。本文实验将输入信号设定为固定的啁啾率，适用于工程实践中特定调频的啁啾信号检测。

参考文献