基于虚拟矩阵的地区虚拟联盟研究与实现

Research and Implementation of Regional Virtual Alliance Based on Virtual Matrix

摘要: 随着全球一体化的产业链和供应链逐渐变得碎片化和区域化，地区化物流需求不断增长。中小企业由于资源受限，无法独立完成跨国物流作业，因此和地区内的海外物流企业进行纵向合作是一个有效的解决途径。本文提出一种适用于区域化环境的地区虚拟联盟合作组织模型。该模型基于电子化联系，采用虚拟矩阵结构，以电子化信息系统作为一体化关键。与传统联盟和一般虚拟组织相比，该模型的绩效控制机制有助于增强组织协调能力，从而使地区物流网络组织更加稳定。在物流链节点的实时信息交换中，使用基于物联网技术的物流应用，可以进一步强化电子化信息系统作为绩效控制机制的重要组成部分。此外，该模型引入了语言变量和多级模糊系统对影响因素进行综合评价，使其更具实用性。该模型为中小型物流企业以低成本进行跨国物流网络建设提供了有价值的参考。

Abstract: As global industry and supply chains become increasingly fragmented and regionalized, the demand for regionalized logistics continues to grow. Due to limited resources, small and medium- sized enterprises cannot independently complete cross-border logistics operations, so sequential cooperation with overseas logistics companies within the region is an effective solution. This paper proposes a regional virtual alliance cooperation organization model applicable in a restricted environment. The model adopts a virtual matrix structure based on electronic contacts, using electronic information systems as key integrations. Compared with traditional alliances and general virtual organizations, the performance control mechanism of this model helps enhance organizational coordination, making the regional logistics network organization more stable. Furthermore, in the real-time information exchange at logistics chain nodes, the use of logistics applications based on Internet of Things technology can further strengthen the role of electronic information systems as an important component of performance control mechanisms. Furthermore, by using of linguistic variables and multi-level fuzzy systems, this model is more practical for comprehensive evaluation of influencing factors. It provides a valuable reference for small and medium-sized logistics enterprises to build a low-cost cross-border logistics network.

1. 引言

贸易全球化、供应链和产业链一体化趋势的发展，曾经带来了全球范围内的物流需求增长，但近年来，贸易保护主义抬头，传统的全球供应链和产业链出现了断裂，变得碎片化。双边和地区性贸易合作也越来越多，譬如区域全面经济伙伴关系协定(RCEP)、跨太平洋伙伴关系协定(CPTPP)等地区性的多边贸易协定正在改变着世界经济和国际贸易。据统计 [1] ，2021年亚洲的出口中，有59%来自该地区的内部贸易。亚太地区已成为全球最大的海运装载卸货地，以及最大的航空货运市场之一 [2] 。在新冠疫情危机以后，更多的区域内投资和贸易发展将进一步强化区域价值链，并为地区经济带来繁荣 [3] 。目前我国物流市场主体中，大部分是中小微企业，但由于缺乏人力、物力以及技术等资源，中小物流企业(Small and Medium-Sized Logistics Enterprises, SMLEs)很难在和大企业共存的市场中获得竞争优势，即使在区域化市场，SMLEs仍然很难独立满足企业所有物流需求。它们迫切需要寻求一种不同于大企业的新模式，以突破国家或地区的边界，寻找合适的合作伙伴，形成配合作业的跨国网络，譬如成立适应区域化物流需求的联盟等。因此，本文提出了适用于区域化环境的一种组织模型：SMLEs地区虚拟联盟。

2. 文献综述

目前，国内外学者对企业间合作模式进行了深入研究，其中联盟是一种常见形式。联盟通常指企业战略联盟，是两个或两个以上的企业为某种共同的战略目标而形成的合作。联盟的形式多种多样，具体取决于联盟的目标、参与者特点和各种限制条件等。常见形式有传统联盟、虚拟组织等。传统联盟的形式包括有：基于“买方–供应商”形成的供应链联盟 [4] ，以及采购、生产、物流商的一体化联盟 [5] ，或所有成员均为物流商的联盟 [6] ，有相对长期性。虚拟组织包括虚拟企业、虚拟联盟等，属于临时联盟。虚拟企业是一种临时的机会主义联盟 [7] ，指来自不同企业的人力、物力、技术等资源具有“插头相容性”，通过电子化联系将这些资源汇聚形成一个电子商业实体，如同联合成一个公司，合作完成共同任务，致力于新项目、生产新产品，以迅速进入市场。它作为一种动态联盟，其存在取决于项目需要，旨在一个多实体平台上实现降低成本和多样化风险。虚拟联盟和虚拟企业有相似之处。从单个成员角度来看，企业合作形成一个虚拟实体，可称为“虚拟企业”；从整个组织角度来看，合作的成员形成了多个虚拟企业，这些虚拟企业又构成了联盟，即“虚拟联盟”。虚拟企业和虚拟联盟均以电子化联系为基础，共享资源和技能，以共同项目任务为目标。随着全球一体化的发展，它们在航空航天、汽车制造等领域越来越普遍 [8] ，甚至促进了地区一体化的进程 [9] 。

采用任何联盟组织形式时，企业间合作都应体现共同目标、中间机制和预期共享利益的特点，以实现两个或以上独立企业的联合行动 [10] 。这种合作必须以信任为基础 [11] 。中间机制作为企业间组织协调的水平关系，在传统与电子化联系方式的发展中体现了联盟的进化。联盟形式不仅能促进企业间的协调和合作，还应提高其在市场上的竞争力和发展能力。

然而，在已有的研究和文献中，关于联盟的讨论较少涉及中小企业，也缺乏专门针对这些SMLEs企业进行研究的成熟模式。实际上，大公司中也存在以地区性业务为主的情况。Collinson等 [12] 研究了亚洲115家世界500强公司，结果发现其中105家公司的主要业务为地区性的，而不是全球业务。因此，在区域化的业务需求下，需要建立相应的地区物流网络来支持运营，从而提出了适用的SMLEs地区联盟模型，该联盟基于电子化联系，采用虚拟矩阵结构，以电子化信息系统为一体化关键，并可借助于物联网技术进一步加强以电子化联系为基础的组织协调，同时引入语言变量和多级模糊系统，对影响因素进行综合评价。该模型为中小物流企业提供了一种在资源有限情况下，形成专业化优势，以低成本实现国际化网络的途径。

3. SMLEs地区虚拟联盟模型

3.1. 定义

基于传统联盟、虚拟企业和虚拟联盟的分析，本文提出SMLEs地区虚拟联盟，从而以低成本实现资源共享。该联盟由国内和海外独立的SMLEs组成，旨在共同完成跨越边界的任务，成员之间具有相互信任和相容性，共享资源、利益和共担风险，并通过组织虚拟化和联系电子化实现合作，拥有绩效控制机制。相对于一般虚拟组织，该联盟长期稳定，合作不会影响成员的独立地位。

3.2. 影响因素

表1对比说明了传统联盟、一般虚拟组织和地区虚拟联盟的影响因素。

Table 1. Factors of SMLEs’ regional virtual alliance

表1. SMLEs地区虚拟联盟影响因素

3.3. 组织结构

多家企业合作，参与单一物流产品的不同环节，形成虚拟职能结构；如果涉及多种产品，则需构建矩阵式结构，这称为“虚拟矩阵式结构”。这种合作可由两家及以上成员组成。图1以两成员联盟的虚拟矩阵式结构为例。假设甲是国内一家物流企业，采用职能制组织结构，包括操作、质量控制及市场营销等部门，各职能部门间通过信息系统横向水平联系。乙是海外类似结构的物流企业。当独立的国内甲企业和海外乙企业建立联盟后，即形成物流链上下游纵向合作节点。通过电子信息系统将甲和乙类似职能部门联系起来，合并成同一虚拟部门，譬如将来自原操作、质量控制及市场营销等部门的专家网络小组人员组成各虚拟部门，这种跨职能的水平虚拟结构，加强了组织间的协调联系，便于绩效控制使组织更稳定。增加的虚拟结构，以电子化联系为基础，加强了组织协调和绩效控制机制。如在物流链节点实时信息交换中，进一步采用基于物联网技术的应用及仿真技术，可实现加快实时信息的传输速度 [21] ，或对物流问题进行优化、提高作业效率 [22] ，从而强化电子化信息系统作为绩效控制机制的重要组成部分。

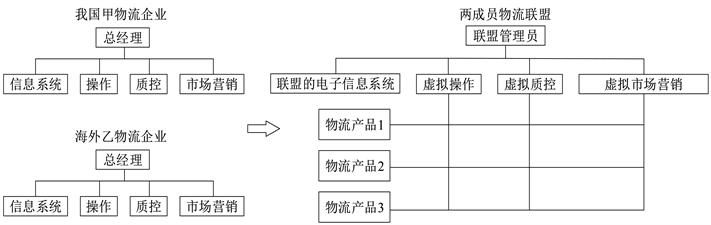
Figure 1. Alliance structure for SMLEs’ logistics companies with virtual matrix

图1. 具有虚拟矩阵的中小物流企业联盟结构

4. 评判过程

4.1. 评判方法

根据SMLEs地区虚拟联盟定义及组织结构，本文给出了评价实现方法，包含三个步骤：

首先，对各影响因素整理细化，并按类似属性分层和分组，在此基础上，采用1~9标度法，将各因素两两比较相对重要性，可得判断矩阵，计算矩阵特征向量并归一化，经一致性检验，得分层分组的各权重向量。

其次，采用层次分析法进行各因素的单因素评价，将各因素看作语言变量，并赋予模糊值。将分层分组的各权重向量正规化，与各因素的语言模糊值结合，使用模糊综合评判方法，按从低到高的层次，进行多层评判。根据最终综合评判值，依照模糊理论最大隶属度原则，确定各因素综合影响的评价等级。

最后，对以上具有层次分析方法的评判系统与多级模糊系统的关系进行分析，使用比较的方法，论述各模糊系统的区别与联系。

4.2. 因素细化

表2列举了SMLEs联盟细化影响因素，分为目标层、准则层和细化说明。其中，信任因素没有单独被列入准则层中，原因是信任可以属于一种控制机制 [23] ，因此，它与电子化信息管理系统、虚拟职能部门(矩阵式)都属于SMLEs联盟绩效控制机制。

根据类似的属性，本节将准则层因素分为三类一级变量，可见表3。记U₁为共同性因素，包括资源、利益、风险；记U₂表示相容性因素，包含组织结构、信息技术、文化；记U₃为绩效控制机制因素，包括信任、电子化系统、虚拟部门。每一类一级变量中分别包括3个二级变量，分别记为u₁、u₂、……、u₈和u₉，并使用语言进行描述与评价。

Table 2. Detailed factors of SMLEs’ alliance

表2. SMLEs联盟细化影响因素

Table 3. Hierarchical influencing factors of SMLEs’ alliance represented by linguistic variables

表3. 语言变量表示的SMLEs联盟分层次影响因素

4.3. 因素排序及算例

在明确了各因素后，本文按照重要性对各因素进行排序。

首先，确定排序比较方法。影响因素，亦称为变量，可用语言描述其评价值，譬如按程度高低分为非常重要、重要、稍重要、一般和不重要等。在比较各因素相对重要性，即确定它们在整个问题中所占权重时，若因素较多，则很难做出准确判断；若同时比较各因素，可能造成某些因素被遗漏或优先考虑。为解决以上问题，Saaty等学者提出采用对各因素两两比较、并通过比较评价的计量方法——1~9标度法，对比较结果赋值和计算，从而得出各因素的重要性顺序，即权重。然而，考虑到自然语言有模糊性，在比较这些变量时，只是粗略的相对重要性，难以从数据上给出精确的定量计量，因此，无法用传统的方法建立数学模型，并进一步对SMLEs联盟各因素做综合统计分析。鉴于自然语言有模糊性的特点，模糊理论可以对语言变量进行比较分析。因而，本文采用1~9标度法得到各因素权重，同时结合模糊理论对各因素影响结果进行评价，该方法核心在确定因素权重。由于各因素本身存在模糊性，因此因素权重就是一个模糊集 [24] 。

其次，采用1~9标度法是否为合适的标度法。人们区分信息等级极限能力是有限的，分级太多会超越人们的判断能力。骆正清等学者 [25] 提出，在对单一准则排序时，各标度法都有保序性，因此建议使用1~9标度法，该标度法在标度均匀性、可记忆性和可感知性方面均较优，但在一致性和权重拟合度方面表现欠佳。鉴于SMLEs联盟仅对影响因素进行相对重要性排序，本文采用1~9标度法评价上述语言信息，参见表4。

尽管可以对所有因素进行两两比较，但不建议将所有因素放在同一层次进行比较和排序 [24] 。原因之一是难以恰当分配权重：分配因素的权重主要依赖于人的主观判断，而当因素太多时，很难做出准确的判断。另一个原因是无法得到有意义的评判结果：当因素很多时，其归一化权重必然会很小，难以真实反映各因素在整体中的地位，可能会泯没单个因素的评判信息，从而使综合评判无法得出有意义的结果。

根据表3，通过专家问卷，对三类一级变量之间的重要性进行评分，并建立第一级判断矩阵A，求出最大特征根和特征向量，进行归一化，即可得到这三组因素的权重向量，记为 $W\left(w_1,w_2,w_3\right)$ ，其中，w₁、w₂、w₃分别对应于U₁、U₂和U₃。接着，对第一级判断矩阵A进行一致性检验，如果通过，就可以

Table 4. The 1~9 scaling method

表4. 1~9标度法

使用权重向量W。需要注意的是，特征向量需要进行归一化处理后才能作为权重向量W使用，再将W正规化为W^*，才能在评判时使用。然后，对三组二级因素 $U_1\left\{u_1,u_2,u_3\right\}$ ， $U_2\left\{u_4,u_5,u_6\right\}$ ， $U_3\left\{u_7,u_8,u_9\right\}$ 分别进行每组内各因素的重要性评分，并建立第二级判断矩阵A₁、A₂、A₃，分别对应U₁、U₂、U₃。同样使用最大特征根和特征向量的方法，求出U₁、U₂、U₃每组内各因素的权重向量，分别记为 $W_1=\left(w_{u1},w_{u2},w_{u3}\right)$ ， $W_2=\left(w_{u4},w_{u5},w_{u6}\right)$ 和 $W_3=\left(w_{u7},w_{u8},w_{u9}\right)$ ，其中w_u1、w_u2、……、w_u8和w_u9，分别对应u₁、u₂、……、u₈和u₉。从而得到二个层次的九个因素相对重要性(权重)。

以U₁组为例，组内含u₁、u₂和u₃，20名专家按1~9标度法，进行组内三个因素两两比较并打分，结果详见表5；根据分数值，系统可以计算出表6中的u₁、u₂、u₃的置信区间。

Table 5. Intragroup comparison of U1 by 1-9 scaling method

表5. 1-9标度U₁组内比较

Table 6. Confidence intervals for factors of U1 group

表6. U₁组内各因素的置信区间

由于该样本只有20个，属于小样本，因此需要使用学生氏t分布来计算置信区间。以u₁为例，具体包括以下两个步骤：

步骤一：计算置信区间。学生氏t分布公式为

$t=\frac{\left|\bar{x}-m\right|}{S/\sqrt{n-1}}$

其中， $\bar{x}$ 为均值，m为u₁的数学期望，S为样本标准差，n为样本个数。假设置信度为0.90，t为对应随机变量值，则 $t\approx 1.7$ ，可以求得u₁的置信区间为2.7 ± 0.68。同理，可得到u₂的置信区间为3.6 ± 0.37，以及u₃的置信区间为1.3 ± 0.29。为了提高精度，也可以采用置信度为0.95或0.99。

步骤二：验证样本数。本步骤将验证对于给定的三个因素u₁、u₂和u₃，样本量为n = 20是否满足最小样本量 $n_{\min }$ 要求。设t为随机变量分布的临界值，采用置信度为0.90时，t = 1.7进行计算。若以此置信度的概率，保证样本均值与总体均值的偏差不超过给定的最小偏差Δ，则可以推导出样本量不小于最小样本量 $n_{\min }$ 。具体为：已知 $\Delta =t\cdot \sigma /\sqrt{n}$ ，则 $n=t^2\cdot {\sigma }^2/{\Delta }^2$ 且 $n\ge n_{\min }$ 。在采用1~9标度进行评分时，设定 $\Delta =0.5$ ，总体标准差 $\sigma$ 可用 ${\sigma }_{估}=\bar{R}/d_2$ 估计，其中， $\bar{R}$ 表示20个样本分成相同大小二组子样时，这二组子样极差的平均数，d₂是一个与子样本大小有关的常数，当子样本数量等于10时，d₂ = 3.08，如表7所示。根据计算，u₁的 ${\sigma }_{估}=\bar{R}/d_2=1.2987$ ， $n_{\min }=t^2\cdot {\sigma }^2/{\Delta }^2=19.5$ ，则u₁的最小样本量 $n_{\min }$ 为19.5。同样的方法可以得出u₂和u₃的最小样本量 $n_{\min }$ 分别为4.87和4.87。通过分别取整，求得u₁、u₂和u₃的最小样本量为20、5和5。由于需要对三个因素进行两两比较评分，因此需要选择这三个值中的最大值，即20，作为最终的样本量。因此，选择20名专家评价u₁、u₂和u₃为合理。

Table 7. Subsample-constant d2

表7. 子样—常数d₂

因此，根据表6的置信区间，即U₁组内大小 $u_2\ge u_1>u_3$ ，对照表4的1~9标度，可得u₂比u₁稍重要，u₂比u₃强烈重要。同理，U₂组内 $u_4\ge u_5\ge u_6$ ，U₃组内 $u_8>u_7\ge u_9$ ，以及三组间大小关系 $U_1\ge U_2>U_3$ 。下面以U₁组内比较为例，按比较结果建立判断矩阵，并求各因素相对重要性权重。为计算方便，表8按照 $u_2\ge u_1>u_3$ 顺序递减排列。

Table 8. Judgment matrix of intragroup comparison U1

表8. U₁组内比较判断矩阵

求解因素权重包括以下两个步骤：

步骤一：根据判断矩阵A，计算其特征向量W及最大特征根 ${\lambda }_{\max }$ 。一般而言，计算判断矩阵的特征向量可以采用“和”法或“根”法，本例中采用“和”法。假设判断矩阵A是一个n阶方阵，其中 $a_{ij}$ 表示第i个因素相对第j个因素的重要性评分。设 $W={\left(w_1,w_2,\cdots ,w_n\right)}^T$ ，其中w_i表示第i个因素在特征向量中的权重，T表示转置矩阵，则

$w_i=\frac{1}{n}{\displaystyle \underset{j=1}{\overset{n}{\sum }}\frac{a_{ij}}{{\displaystyle \underset{k=1}{\overset{n}{\sum }}{a}_{kj}}}},i=1,2,\cdots ,n$

可求得归一化特征向量 $W={\left(0.63,0.26,0.11\right)}^T$ ，最大特征根 ${\lambda }_{\max }$ 为3.0387。

步骤二：检验判断矩阵A是否为一致矩阵，即一致性检验。当判断矩阵A的阶数n大于2时，可以比较 ${\lambda }_{\max }$ 与n的大小关系，来确定归一化特征向量是否可作为权重向量，即此时一致性比例CR必须小于某个阈值才能认为判断矩阵A是一致矩阵。在本例中，判断矩阵A的阶数为3，根据一致性指标

$CI=\frac{{\lambda }_{\max }-n}{n-1}$

可以计算出CI = 0.01935，且阶数n = 3时，另一平均随机一致性指标RI = 0.52，两者相除可得一致性比例 $\text{CR}=\text{CI}/\text{RI}=0.0372$ 。一般当CR小于0.10，则认为 ${\lambda }_{\max }\approx n$ ，即此时判断矩阵A是一致矩阵，因此可以使用归一化特征向量W作权重向量。需注意，此权重对应U₁，当 $W={\left(w_1,w_2,w_3\right)}^{\text{T}}={\left(0.63,0.26,0.11\right)}^{\text{T}}$ ，由于此处 $w_1=0.63$ 实为w_u2，以及 $w_2=0.26$ 实为w_u1，而且因为U₁组内的u₁、u₂、u₃对应的特征向量 $W_1={\left(w_{u1},w_{u2},w_{u3}\right)}^T$ ，因此U₁组内的二级权重向量 $W_1={\left(0.26,0.63,0.11\right)}^T$ 。同样的，对于U₂组内和U₃组内的比较，分别得到二级权重向量 $W_2={\left(0.63,0.26,0.11\right)}^T$ 和 $W_3={\left(0.26,0.63,0.11\right)}^T$ ，最终通过三组比较得到一级权重向量 $W={\left(0.63,0.26,0.11\right)}^T$ 。显然，各组内相对权重最大的因素为：u₂利益共享，u₄组织结构相容，u₈电子化信息系统。

4.4. 各因素综合评判及算例

在确定了各因素的重要性排序(相对权重)后，可以考虑它们对联盟的影响，即进行综合评判。假设有9个因素，每个因素都有5个评价模糊集，即评判集 $V=\left\{v_1,v_2,v_3,v_4,v_5\right\}$ ，以某SMLEs联盟为例，共20名专家进行了评价，评价结果如表9，所示数字为某评价比例。

Table 9. Anexample of SMLEs’ alliance comprehensive evaluation

表9. SMLEs联盟综合评判实例

综合评判分为以下三个步骤：

步骤一：对单因素进行评价，建立评判矩阵，并正规化。对三类一级变量组U₁、U₂和U₃二级变量u₁、u₂、……、u₈、u₉，进行各组内单因素评判，得：

$R_1=\left[\begin{array}{ccc}0.25& 0.50& 0.15\\ 0.40& 0.30& 0.20\\ 0.25& 0.30& 0.20\end{array}\begin{array}{c}0.10\\ 0.05\\ 0.15\end{array}\begin{array}{c}0\\ 0.05\\ 0.15\end{array}\right]$ ， $R_2=\left[\begin{array}{ccc}0.25& 0.40& 0.15\\ 0.40& 0.35& 0.15\\ 0.25& 0.20& 0.30\end{array}\begin{array}{c}0.10\\ 0.10\\ 0.20\end{array}\begin{array}{c}0.10\\ 0\\ 0.15\end{array}\right]$ ，

$R_3=\left[\begin{array}{ccc}0.30& 0.20& 0.15\\ 0.40& 0.35& 0.15\\ 0.15& 0.20& 0.20\end{array}\begin{array}{c}0.20\\ 0.05\\ 0.15\end{array}\begin{array}{c}0.15\\ 0.05\\ 0.30\end{array}\right]$ ，

正规化后记作 $R_1^{*}$ 、 $R_2^{*}$ 和 $R_3^{*}$ 。

步骤二：通过评判矩阵和组内权重，可得第一级综合评判，即二级单因素评判矩阵。根据U₁、U₂、U₃组内各因素权重向量W₁，W₂，和W₃，正规化后可得 $W_1^{*}$ ， $W_2^{*}$ 和 $W_3^{*}$ 。再通过使用M (Ù,Ú)合成算子，得到第一级综合评判： $B_1^{*}=W_1^{*}\circ R_1^{*}$ ， $B_2^{*}=W_2^{*}\circ R_2^{*}$ ， $B_3^{*}=W_3^{*}\circ R_3^{*}$ ，则可得二级单因素评判矩阵 $R^{*}={\left(B_1^{*},B_2^{*},B_3^{*}\right)}^{\text{T}}$ 。

步骤三：通过二级单因素评判矩阵和组间权重，可得第二级综合评判。根据U₁、U₂、U₃组间权重向量W，正规化得W^*，则二级评判向量 $B^{*}=W^{*}\circ R^{*}$ ，得综合评判 $B^{*}=\left(1,0.75,0.5,0.25,0.25\right)$ ，归一化得各因素对联盟综合影响 $B=\left(0.36,0.27,0.18,0.09,0.09\right)$ 。同样，如果用其他算子，可得综合评判 $B^{*}$ 及归一化B：

M (∙, Ú)算子： $B^{*}=\left(1,0.75,0.5,0.125,0.125\right)$ ， $B=\left(0.4,0.3,0.2,0.05,0.05\right)$ ；

M (Ù, Å)算子： $B^{*}=\left(1,0.9,0.76,0.57,0.39\right)$ ， $B=\left(0.28,0.25,0.21,0.16,0.11\right)$ ；

M (∙, +)算子： $B^{*}=\left(0.96,1,0.53,0.26,0.18\right)$ ， $B=\left(0.33,0.34,0.18,0.09,0.06\right)$ 。

通过比较各归一化B，不同算子评判结果相差不大，按最大隶属度，前三种综合评判为“好”，第四种“较好”。前三种以主因素为主，第四种亦考虑其他因素。第四种未达“好”原因可能为部分因素评价低，例如u₆、u₉的模糊集v₁的隶属度仅0.15。设改善u₆、u₉，见表10。对于改善后的 $B^{*}=\left(0.98,1,0.52,0.27,0.17\right)$ 指标，可以看出v₁的隶属度从0.96提高到0.98，但根据最大隶属度原则，v₂的隶属度是1，即最终评判结果仍为“较好”。因此，虽然u₆和u₉对SMLEs联盟也有影响，但是它们的权重比较小，在综合评判中的影响不大，影响最大的是各自组内相对权重最大的因素，例如u₄组织结构相容和u₈的电子化信息系统。这种先按类分组求权重，再进行多层评判的方法被称为层次分析法。

Table 10. Improved evaluation of u6 and u9

表10. 改善的u₆和u₉评价

5. 分析与比较

5.1. 性能分析

SMLEs联盟有9个影响因素，每个因素有5个评价语言值，可将这些因素看作模糊系统的输入变量，对联盟影响综合评价则看作模糊系统的输出变量。层次分析法作为一种多级评判方法，也是一种基于语言值模糊集的模糊系统。对于模糊系统，假设n个输入变量，每个变量定义m个模糊集，则该模糊系统规则数为 $m^n$ ，当n较大时， $m^n$ 数值极大，会引发维度灾难问题。本例中，n = 9，m = 5，规则数5⁹ (=1953125)。采用数百万条规则的模糊系统是不现实的，因此需寻求减少规则数的方法。根据Wang学者研究 [26] ，对于模糊系统，可看作是一个输入与输出的非线性映射，多级模糊系统是解决维度灾难的一种方法，设有n个变量，每个变量定义m个模糊集，c为模糊系统各级输入数量，则多级模糊系统规则数

$M=\frac{m^c}{c-1}\left(n-1\right)$

当m ≥ 2，则c = 2时(即模糊系统各级都为二输入时)，规则数M最少。图2给出了c = 2时，有n个输入变量 $x_1,x_2,\cdots ,x_n$ ，输出变量为y，n - 1级的多级模糊系统。

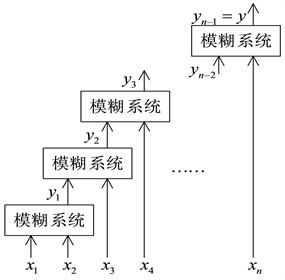
Figure 2. Two-input multi-level fuzzy system

图2. 二输入多级模糊系统

若SMLEs联盟变量数n = 9，每个变量的模糊集取m = 3时，取值分别为好、一般、差；当m = 5时，取值分别为好、较好、一般、较差、差，则可得较高精度。当c = 2时，最少规则数M为200 (= 5²∙(9 − 1))。但实际中，即便符合各级二维输入的条件，规则数也不一定能达到最少。因为可能存在两个因素的相对重要性无明显差异，即并非任意两个因素都可比较，需加入其他因素比较，使该级有三个因素比较(比如x₁先与x₂比较，发现无明显差异，再将x₁与x₃比较，该级x₂与x₃未比较，因为该级x₁参与了两次比较，相当于增加一个x₁因素，这时并非该级为三维输入，而是多了一级二维输入)，因而总因素数增加，并将导致规则数M增加，而达不到c = 2时的最少规则数，因而此200个规则是极限。SMLEs联盟例子中，有9个变量，每个变量有5个评价语言值，如采用层次分析，以分层分组方式输入，第一层3个变量，每个变量5个模糊集，规则数为125(=5³)；第二层3个组，每组3个变量，每个变量5个模糊集，规则数为125(=5³)，3组共375个规则，两层共500个规则，远少于1953125个规则，因此，层次分析法减少规则有一定作用，虽仍多于二维输入系统规则，但就1953125个规则而言，减至500个已相对接近极限200，且同数量级。而且二维输入系统，要求各级两个输入，层次分析法未限各级输入数，而先根据类似属性对因素分组，再多级输入，分组分级有合理性，易于因素比较。因而，此M = 500可看作一个解，对应的评价方案有一定实用性。层次分析法中，不同分组方法会有不同M值(如果存在不同分组)，应比较各M值，取小者。表11列出了各模糊系统的比较。

Table 11. Comparison of different fuzzy systems

表11. 不同的模糊系统的比较

5.2. 成员数量的有限性与比较次数

一个联盟至少要有两个成员，如果成员较少，显然组织协调控制相对容易，但是关于联盟成员数量的最大限制，现有文献资料涉及较少。本文从成员间比较次数的角度进行探索。假设联盟有s个成员 $M_1,M_2,\cdots ,M_s$ ，单因素两两比较，则比较次数为组合数 $C_s^p$ ，即s个成员，每次任意取p = 2个，比较次数为

$C_s^p=\frac{s!}{p!\left(s-p\right)!}=\frac{s!}{2!\left(s-2\right)!}=\frac{s\left(s-1\right)}{2}$

当成员数s为10时，比较45次；当s较大时，由于虚拟职能部门的矩阵结构，存在共同性、相容性、绩效控制等多因素比较，成员间协调关系比较复杂，比较次数非常多，因此要采取方法减少比较次数。一种方法是，将具有标准化比较依据的成员M₁作母本，其他成员 $M_2,M_3,\cdots ,M_s$ 分别和M₁比较(余s - 1个成员，每次取不重复的某个比较)，此时p = 1，需比较 ${\text{C}}_{\text{s-1}}^{\text{1}}\text{=s}-\text{1}$ 次，当s为10时，需比较9次(=10 − 1)。并且，当各成员为多因素时，每个成员n个因素，p = 2和p = 1分别需比较 $ns\left(s-1\right)/2$ 和 $n\left(s-1\right)$ 次，且因 $s\ge 2$ ， $n\ge 2$ ，则 $ns\left(s-1\right)/2\ge n\left(s-1\right)$ ，显然p = 1时，比较次数较少，如表12所示。

Table 12. Comparison times

表12. 比较次数

尽管SMLEs联盟依赖电子信息系统，可以缓解组织协调问题，但不同企业整合时，各自电子信息系统兼容(相容性)或数据标准化程度会产生新的问题，增加更多比较次数，从而影响组织协调效果。而且虽利用物联网应用和仿真技术，可对某些常见物流问题进行优化，提高组织协调效率，但当成员数量较多、且影响因素也较多时，由于SMLEs联盟组织结构的特殊性导致的协调的复杂性，则较难得到合适的优化方案。因此，成员数量是有限的，不能无限增加。另一方面，由于成员数量有限，且联盟是基于物流链纵向环节建立的。因而决定了物流链的最大长度，譬如，我国物流商与海外方合作，是限于对方机场或港口口岸的场站服务，还是覆盖最后一公里，包括配送到门。此外，这也限制了物流链的宽度，即纵向发展是覆盖一个国家的一条航线，还是跨越多个国家的多条航线。因此，SMLEs联盟的发展需要考虑成员数量和地域范围等方面因素，以确保联盟的协调和配合效果。

6. 结语

在区域化贸易环境下，为应对产业链和供应链相应的物流需求，本文提出了一种SMLEs实现国际化的方法，即与海外物流商合作建立基于电子化联系的地区虚拟联盟。该方法通过选择专家人员组成网络小组，采用矩阵结构设立虚拟职能部门，以水平联系加强组织间协调，这样便于绩效控制以及使得组织更加稳定，并注重物流链纵向环节的关键职能节点，以形成专业化，从而实现取得协同增效利益共享。分析表明，联盟组织受多种因素影响，其中，利益共享、组织结构相容、电子化信息系统是相对影响较大的因素。如果对各因素按类似属性分组，借助语言变量，则可通过层次分析方法的多级模糊系统对各因素综合评价，因而该模型有一定实践意义。未来工作将聚焦成员数量的有限性问题，通过研究其在电子化系统和其他因素影响下最大值的可能性，进一步摸索虚拟联盟的可行区域范围。