基于ANSYS的系列铜管夹具优化设计

Optimization Design of Series Copper Pipe Fixture Based on ANSYS

摘要: 针对四通阀铜管在管端倒角作业中的装夹问题，设计了一种采用外圆定位装夹的系列铜管握夹夹具，实现了对于系列铜管内管面无损伤的定位装夹。夹具结构初步设计后，对夹具装夹的铜管进行静力学分析。验证出铜管变形未超出工艺要求，证明了夹具结构的可行性。之后针对各设计参数进行灵敏度分析，通过响应面法优化设计参数，保证在不增大夹具整体质量的情况下，铜管所产生的静变形量和最大等效应力最小。结果表明：在保证夹具整体质量的情况下，铜管所受最大变形量减少了24.4%，最大等效应力降低了28.5%。

Abstract: Aiming at the clamping problem of four-way valve copper pipe in the chamfering operation, a series of copper pipe clamping fixture with cylindrical positioning is designed to realize the non-damaging positioning clamping of the inner tube surface of the series copper pipe. After the preliminary de-sign of the fixture structure, the static analysis of the clamping copper pipe is carried out. It is veri-fied that the deformation of the copper pipe does not exceed the technological requirements, which proves the feasibility of the fixture structure. Then the sensitivity analysis of each design parameter is carried out, and the response surface method is used to optimize the design parameters to ensure that the static deformation and the maximum equivalent stress of the copper tube are minimized without increasing the overall mass of the fixture. The results show that the maximum deformation of the copper pipe is reduced by 24.4% and the maximum equivalent stress is reduced by 28.5% when the whole quality of the fixture is guaranteed.

1. 引言

图1为某企业的制冷四通阀，其专用铜管采用TP2磷脱氧铜制成，作为四通阀的重要组成部件，在市场上需求量巨大 [1] 。铜管的倒角作业有两种方法：一种是将铜管装夹在倒角机工作台上进行倒角加工处理，另一种将其安装在三爪卡盘上利用车床进行倒角作业 [2] 。因为两种装夹方式目前大都采用人工作业，所以装夹时间比较长，自动化改造成本较高。且在多次装夹后会产生一定的误差，形位精度和加工质量难以保证。此外，其在空间布局以及自动化加工工艺上也无法满足新型倒角设备的加工需求 [3] [4] 。因此本文根据系列铜管的形状结构特点，进行详细的工艺分析，综合分析同系列不同型号的接管尺寸，设计了一种适用于系列铜管倒角加工的专用夹具，并通过ANSYS有限元分析软件对其进行仿真优化来提高系列铜管握夹装置的可靠性。

Figure 1. Refrigeration four-way valve

图1. 制冷四通阀

2. 四通阀铜管装夹方案

专用铜管为变口径管状结构，两端面直径不同。铜管小口径端面根据工艺要求需要倒出45度斜角以便于提高后续铜管与阀体的装配效率。在类似管状结构的倒角加工过程中，通常会采用双涨式夹具或三角卡盘进行装夹作业，这两种装夹方式在手工作业时可操作性高，具有一定的工作效率。但经过综合分析后发现，铜管零件加工小口径端面时，采用上述方式装夹铜管时会有以下几个问题。

1) 在进行双涨式夹具装夹时，定位所需的定位杆在插入铜管零件内径中时，不可避免的损伤铜管内表面，从而加剧铜管内制冷媒介对于铜管的腐蚀作用。

2) 由于铜管为变口径管状结构，大口径端面较短，在装夹铜管端面时双涨式夹具的定位杆与铜管整体之间无法实现完全配合。在对管端进行倒角作业时，由于切削力等因素会使铜管零件振动，从而影响加工的精度和安全 [5] 。

3) 在采用三爪卡盘进行铜管装夹时，考虑到铜管大口径端面可装夹长度短小，从而导致装夹面积减小，相应夹紧力增大，产生装夹部位过大变形的现象。

针对以上问题，系列铜管夹具采用外圆定位的外表面装夹方式避免了铜管内径表面的损伤，同时装夹铜管较长的小口径端可以增大装夹面积，限制了装夹部位过大变形的现象，系列铜管夹具装夹示意图如图2所示。

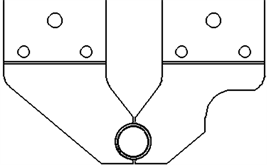(a) 正视图 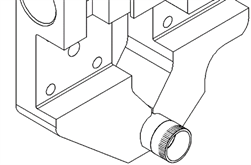(b) 轴测图

Figure 2. Clamping diagram

图2. 装夹示意图

3. 夹具结构设计

根据上述系列铜管的装夹方式分析，夹具结构采用图3所示的A基准平面定位，B基准外圆定位与夹手夹紧的结构形式，同时设置定位块来限定夹持压力大小。铜管到达堆料区后，推杆推动铜管大端，将其A基准平面顶靠在定位板上，完成X轴的定位。然后夹具夹手夹紧B基准外圆表面，由夹手夹紧力实现那对于铜管的完全固定。夹具整体结构简单、由液压油缸推动夹具实现夹紧和放松，通过夹具与铜管外表面的静摩擦力提供作业时的夹紧力，进行装夹作业。图4为系列铜管夹具的整体结构图。

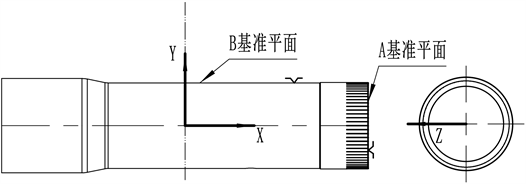
Figure 3. Schematic diagram of copper pipe positioning

图3. 铜管定位示意图

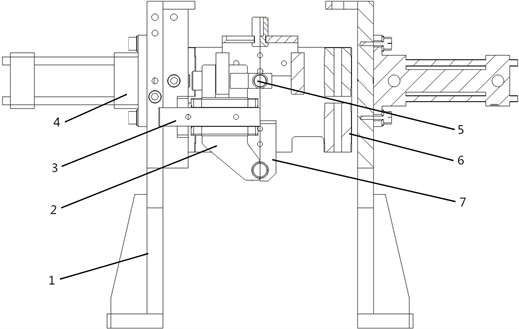1——夹具底座；2——夹具夹手；3——夹手导轨；4——液压油缸；5——限位块；6——滑块；7——定位板

Figure 4. Series copper pipe fixture structure diagram

图4. 系列铜管夹具结构图

4. 夹具装夹静力学分析

4.1. 模型导入及材料添加

夹具的总体结构设计完成后，将所设计三维模型导入到有限元分析软件ANSYS中进行参数优化。模型导入后进行材料的选择，经查阅材料选择TP2磷脱氧铜，密度为915.7 Kg/m³，弹性模量为132 GPa，泊松比为0.34 [6] 。

4.2. 网格划分

在网格划分时，为进一步提高网格质量且兼顾计算精度和速度，将网格最小尺寸限制定义为1 mm。网格划分图与网格质量分布柱状图如图5所示，通过对柱状图的分析可知，铜管的元素数量大都集中在0.75左右，说明划分的网格质量良好。

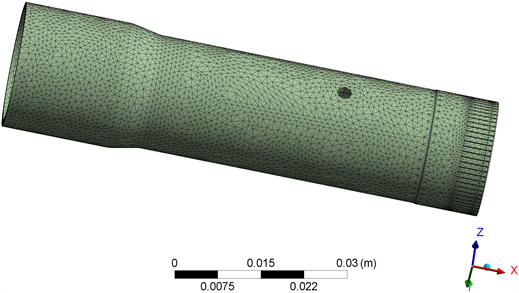(a) 网格划分图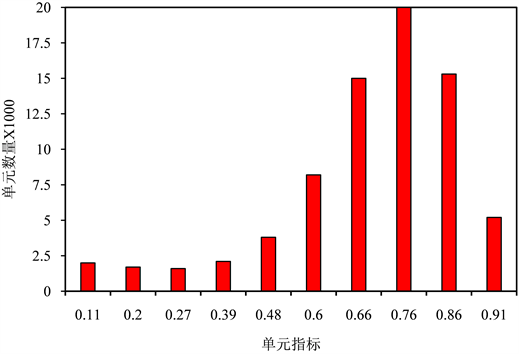(b) 网格质量柱状图

Figure 5. Detailed grid division

图5. 网格划分详细图

4.3. 载荷和约束施加

在铜管的作业过程中，铜管主要受的载荷有夹具的夹紧力和刀具作业时对铜管产生的切削力，经过理论计算夹具用于固定铜管的夹紧力P = 4540 N；倒角作业时对于铜管产生的切削力F = 454 N。其载荷施加如图6所示。

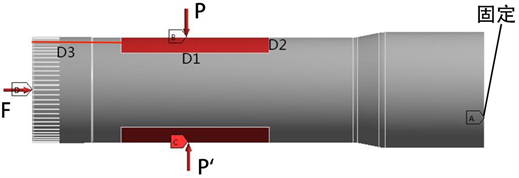
Figure 6. Schematic diagram of load application

图6. 载荷施加示意图

4.4. 计算结果分析

通过Solution分析计算，可获得铜管模型的等效应力云图和等效位移云图如图7，图8所示。

图7中铜管的外表面变形量由装夹处向中心呈阶梯状递增，其中铜管中间小孔处的变形量最大，为87.4 μm，小于铜管工艺限定的最大变形量。由此可得，夹具的整体结构设计符合要求，但在此基础上也可进行进一步优化。

由图8可以看出，铜管外表面装夹处所受的应力呈对称分布且向铜管中间逐渐增大。图8的等效应力云图可知，等效应力最大值为468 MPa，有一定的应力值安全范围，但数值偏大，需进一步优化处理以降低等效应力值。

Figure 7. Static deformation diagram

图7. 静变形量图

Figure 8. Equivalent stress cloud map

图8. 等效应力云图

5. 夹具响应面优化设计

响应面试验是一种利用合理的试验设计方法并通过试验得到一定的数据，之后采用多元二次回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最有工艺参数，是解决多变量问题的一种统计方法 [7] 。利用响应面法进行结构优化设计是如今结构优化领域研究的热点，可以有效的减小传统优化设计计算量大、耗费时间长等缺点 [8] 。

5.1. 设计参数的选择

夹具的设计参数较多，在进行优化时不可能将所有的参数都进行优化。因此需要选择对于最大等效应力和最大变形量影响较大的参数进行优化。灵敏度分析不仅可以显示设计变量对输出结果的影响，而且能够直观的看出各设计变量对于输出结果影响程度的大小 [9] 。经过分析，可得到如图9所示的灵敏度柱状图，显示出3个设计参数(D1、D2和D3)对于目标结果影响程度的大小。

Figure 9. Histogram of sensitivity

图9. 灵敏度柱状图

由图9可知，夹具握夹距小端面距离(沿X轴方向) D3和夹具握夹宽度(沿Y轴方向) D2两个设计参数对于铜管的静变形量和最大等效应力的影响较大，这两个设计参数对铜管的影响都在0.6以上；夹具握夹长度(沿X轴方向) D1对于铜管的影响灵敏度在0.3左右。

将设计参数夹具握夹宽度(沿X轴方向) D1，夹具握夹弧长(沿Y轴方向) D2，夹具握夹距小端距离(沿X轴方向) D3为输入参数，将铜管外表面所受最大等效应力以及铜管的最大变形量设定为输出结果，其中设计参数初始值和变化范围如表1所示。

Table 1. Design parameters and variation range

表1. 设计参数及变化范围

5.2. 试验点的选取

拟合响应面试验样本点的选取技术(DOE技术)有许多种试验设计方法，如Central Composite Design (CCD)、Box-Behnken Design (BBD)、Plackeet-Burman (PB)等，本试验设计采用较为广泛的CCD法。通过响应面系统中的DOE组件，利用CCD方法对于3个设计变量共产生15个试验点，试验设计数据如表2所示。

Table 2. DOE test design data

表2. DOE试验设计数据

5.3. 响应面模型构建

响应面优化通过采用多项式回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优工艺参数，根据优化变量和对应的响应值，建立拟合模型，目标函数与优化变量的拟合多项式可表示为

$y\left(x\right)=a_0+{\displaystyle {\sum }_{i=1}^m{a}_i{x}_i}+{\displaystyle {\sum }_{i=1}^m{a}_{ii}{x}_i^2}+{\displaystyle {\sum }_{i=2}^m{\displaystyle {\sum }_{j=1}^{i-1}{a}_{ij}{x}_i{x}_j+\epsilon }}$

式中， $x_i$ 为设计变量，m为设计变量个数， $a_0$ 、 $a_i$ 、 $a_{ii}$ 、 $a_{ij}$ 为多项式的待定系数， $\epsilon$ 为误差项。

通过设计点预测值与观测值的对比考查模型的拟合精度，装夹过程中铜管的最大变形量和最大等效应力预测值与观测值分布如图10所示。由图10可知，铜管输出参数的响应面预测值与仿真观测值拟合效果良好。

Figure 10. Design point predicted values

图10. 设计点预测值

通过CCD中心组合设计实验法进行标准二阶响应面建模，得到如图11所示的响应面模型图。

从图11(a)中可以看出，最大变形随着设计参数D2的增大而增大，呈负相关趋势在D2的改变下，D3整体影响较小，不过在D3处于15 mm左右时，影响最为严重。当D2取得最大值时，铜管的最大变形量处于最大值。从图11(b)可以看出，响应面图形类似于网兜状，设计参数D1对于铜管的最大等效应力影响在35 mm处较大，设计参数D3对于铜管的最大等效应力影响于15 mm处呈对称分布，有降低相趋势。

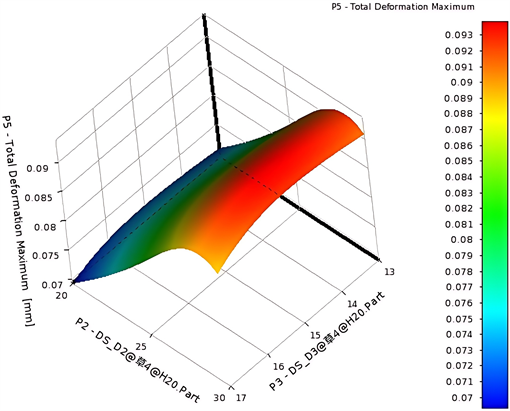(a) 最大变形响应面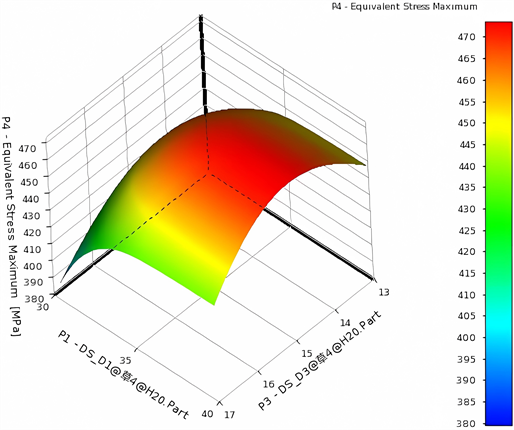(b) 最大等效应力响应面

Figure 11. Response surface model diagram

图11. 响应面模型图

5.4. 多目标遗传优化算法优化

在寻求全局最优解时，系统将所建立的响应面表达式传递到优化模型当中，并采用MOGA多目标遗传优化算法进行优化，该算法是一种全局优化算法，多适用于处理连续设计变量的多目标优化问题，在满足所有约束和各个目标函数的条件下，求解出最优的一组解 [10] 。在进行优化时，将初始种群设置为100，每次迭代100个样本，最大允许遗传代数为20代。经过多目标遗传算法与帕累托法进行计算后，得到如表3所示的3个候选解。

Table 3. Candidate solutions of design points

表3. 设计点候选解

由表3可以看出，3组候选解的最大等效应力和最大变形量都没有超出限定的安全范围。但优化的主要目的是在满足夹具夹持面积最小化的前提下，尽可能的降低铜管装夹时的最大等效应力和最大变形量。综合分析，候选解1的变形量和等效应力都小于其他两个候选解，因此候选解1最优设计变量组合，优化后最大静变形量为66 μm，最大等效应力为334.2 MPa。经过优化后的设计参数，使得铜管在满足夹具在不增大整体体积的前提下，所受最大等效应力降低了28.5%，最大静变形减少了24.4%。

6. 总结

1) 本文通过对系列铜管零件的倒角工艺和装夹方式进行分析，综合考虑各种装夹方式的优缺点，并结合自动化加工要求，采用了外表面装夹法进行铜管装夹定位。根据装夹方式确定夹具的整体结构，设计出一种系列铜管夹具。

2) 利用有限元软件对装夹过程中的铜管进行静力学分析，可以得出，铜管的最大静变形和最大等效应力发生在铜管被装夹处和中间小孔处，其数值都在限定的安全范围，验证了夹具整体结构设计的可行性，但其数值偏大的，在此基础上仍可进一步优化。

3) 在ANSYS有限元软件对铜管进行静力学分析的基础上，采用响应面法建立设计变量与目标之间的模型，确定各设计参数对最大静变形量和最大等效应力的影响程度，并采用多目标遗传算法MOGA求解选优，获得了优化的系列铜管握夹结构的设计方案，经优化后的最大静变形量减少了24.4%，最大等效应力降低了28.5%。