1. 引言
Tutte多项式是由Tutte [1] 在1954年提出,是著名的图多项式不变量之一,它提供了关于图结构的各种有趣的信息,能很好地反映图的一些性质及特征。Tutte多项式的应用十分广泛,并且与许多学科存在紧密的联系,例如在计算机科学、工程、优化、物理、化学、生物学和纽结理论等,也是求解图参数的一个重要工具。1985年,Jones [2] 通过冯–诺依曼数组将Jones多项式定义为纽结不变量。目前计算Jones多项式有多种方法,其中利用拆接关系去计算纽结和链环的方法较为常见,但是针对交叉点数较多的纽结和链环来说计算较为复杂,于是众多学者开始探索更简便的方法去计算Jones多项式。1987年Kauffman在 [3] 中介绍了Jones多项式的状态和模型,提出了Jones多项式与尖括号多项式、拧数的等式关系。陶志雄利用二项式的知识研究了特殊环面结的Jones多项式 [4] ,Kwun Y C等学者通过Tutte多项式与Jones多项式之间的关系计算了各边均为正号的
图对应链环的Jones多项式 [5] 。
本文的组织结构为:在第2节中,我们给出一些关于图和纽结的基本概念,以及Tutte和Jones多项式的定义。此外,在这一节中,我们给出了图和纽结之间的关系,以及Tutte和Jones多项式之间的关系,在第3节给出主要结果。
2. 预备知识
2.1. 图
图G定义为一个偶对
,记作
,其中:
1) V是一个有限的非空集合,其元素称为顶点或点,用
表示顶点集合;
2) E是无序积
中的一个子集合,其元素称为边,且集合
中的元素在E中可以重复出现多次,用
表示边的集合。
3) 一条边x,y被称为连接顶点x和y,用xy表示;顶点x和y是这条边的末端顶点。如果
,那么x和y是G的相邻顶点,并且顶点x和y与边xy相伴。如果两条边正好有一个共同的端点,那么它们就是相邻的 [6] 。
2.2. 对偶图
设图G的对偶图为
,则
满足以下两点:
1)
的每一个顶点对应G的每个面;
2) 如果图G有一条边把两个面隔开,则
在图中代表图的两个面的点之间有一边相连,同一个面被一条边隔开,则这个面对应的点有一个自环(如图1所示)。
2.3. 链环
将若干个互不相交的圆
嵌入三维欧式空间
中或球面
中,由这些圆形成的空间图形称为链环,记为
。在此之中n为链环L的分支数,
称为L的一个分支。若通过合痕后所有的
都是平凡纽结,则此时称L为平凡链环,若给定每个分支一个方向,便可得到一个定向链环,当
时,链环只有一个分支,称为纽结 [6] 。

Figure 1. The move process from Figure G to dual figure
图1. 图G到对偶图
的变换过程
2.4. 纽结和图之间的联系
每个链环投影图,我们可以找到一个对应的有符号平面图,反之亦然。这个过程如下:
1) 假设K是一个纽结,K'是它的投影。投影K'将平面划分为几个区域。从最外层的区域开始,我们可以将这些区域染成白色或黑色。使边缘两侧的颜色永远不会一致。
2) 若我们把最外层的区域染成白色,在每个黑色区域选择一个顶点。如果两个黑色区域R和R'有共同的交叉点
那么我们用边连接R和R'的选定顶点,这些边穿过
并位于这两个黑色区域中。这样,我们从K'得到一个平面图G [7] ,如图2所示。
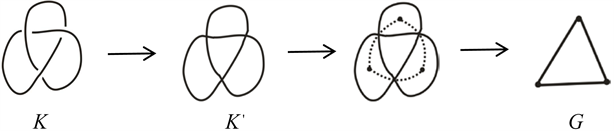
Figure 2. Figure G corresponding to the knot projection K'
图2. 与纽结投影图K'相对应的图G
我们给图G的每条边分配符号+或−,如图3所示。
通过上述过程形成的图被称为纽结K所对应的有符号平面图,如图4所示。
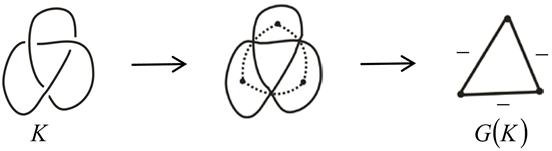
Figure 4. Symbol diagram corresponding to the knot diagram
图4. 与纽结图相对应的符号图
反之,任一符号图,我们可以找到对应的链环图。从图5中可以清楚地看到这个构造。
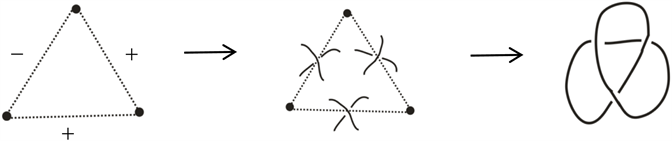
Figure 5. Link diagram corresponding to symbol diagram
图5. 符号图对应的链环图
2.5. Tutte多项式
[8] 图G的Tutte多项式
可以定义为:
其中
和
分别表示图G删除边e和收缩边e后得到的图。
性质1:设
是G和G'的不交并,
是
当且仅当为一个顶点,则有:
性质2:长为n的循环图
的Tutte多项式为:
2.6. 拧数
一个链环L的有向投影图,对其一个交叉点,我们将上行线旋转到下行线,并找到所扫过的最小转角,若此过程为逆时针旋转,则此交叉点记为+1;若此过程为顺时针旋转,则此交叉点记为−1,称链环L全体交叉点的+1和−1的总和为链环L的拧数,记为
[6] 。
2.7. Jones多项式
对于有向投影图L的Jones多项式
是变元为
的Laurent多项式,满足如下拆接关系:
并且平凡结的Jones多项式为1。这里
,
和
是三个定向链环,它们的不同之处如图6所示。
2.8. Tutte多项式与Jones多项式的关系
令G是定向交错链环图L的正符号平面连通图,那么链环L的Jones多项式为:
其中
是G中的顶点数,
是G的对偶图中的顶点数,
是L的拧数 [6] 。
3. 花图
对应链环的Jones多项式
本文研究的是一类
花图,定义如下:
如果一个图G有3个顶点,形成一个3-圈,有3个
顶点的集合,这些顶点来自3圈周围的n-圈,因此每个n-圈与3-圈相交于一条边上,则称为
花图,其中
。
有
个顶点和3n条边,n-圈被称为花瓣,3-圈被称为
的中心,构成中心的3个顶点都是4度,所有其他顶点都是2度 [9] 。如图7所示,其中n表示外圈的边数。
3.1.
花图的Tutte多项式
定理3.1
花图的Tutte多项式为:
证明:
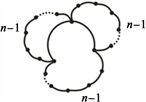


综上,
花图的Tutte多项式为:
花图的Tutte多项式为:
推论3.1
的表达式为:
证明:当
时,有:
3.2. 花图
对应链环的拧数
花图对应链环L可分为两种情况进行讨论,当n为奇数时,L为二分支链环;当n为偶数时,L为三分支链环。
1) 当n为奇数且L的两个分支反向时,分析G,L,
,
,
,如表1所示。

Table 1. n shows odd numbers and the two branches of L are reversed
表1. n为奇数且L的两个分支反向
由表1可见:当n为奇数且L的两个分支L1与L2反向时,
,
,L的所有交叉点处的值均为−1,一共有3n个交叉点,故
;
同理可证,当n为奇数且L的两个分支L1与L2同向时,
,
,L的所有交叉点处的值均为+1,一共有3n个交叉点,故
。
1) 当n为偶数且L的3个分支L1,L2,L3同向时,分析G,L,
,
,
,如表2所示。

Table 2. n shows even numbers and the three branches of L are in the same direction
表2. n为偶数且L的三个分支同向
由表2可知:当n为偶数且L的3个分支L1,L2,L3同向时,
,
,L的所有交叉点处的值均为+1,一共有3n个交叉点,故
;
当n为偶数且L的3个分支L1与L2同向,L3与L1、L2反向时,分析G,L,
,
,
,如表3所示。

Table 3. n is even and the three branches of L, L1、L2 and L3 are reversed
表3. n为偶数且L的3个分支L1、L2与L3反向
由表3可知:当n为偶数且L的3个分支L1与L2同向,L3与L1、L2反向时,
,
,L有2n个−1的交叉点,有n个+1的交叉点,故
;
同理可证,当L1与L3同向,L2与L1、L3反向;L2与L3同向,L1与L2、L3反向时,也是
,
,L有2n个−1的交叉点,有n个+1的交叉点,故
。
3.3. 花图
对应链环L的Jones多项式
定理3.2 当n为奇数时,花图
对应链环L的Jones多项式为:
1) 当链环L的两个分支反向时:
2) 当链环L的两个分支同向时:
证明:当n为奇数且L的两个分支反向时,
,
,
。根据Jones多项式与Tutte多项式:
,将各个参数代入计算得到:
当n为奇数且L的两个分支同向时,
,
,
,将各参数代入
得到:
定理3.3 当n为偶数时,花图
对应链环L的Jones多项式为:
1) 当链环L的三个分支L1、L2与L3同向时:
2) 当L1与L2同向,L3与L1、L2反向;L1与L3同向,L2与L1、L3反向;L2与L3同向,L1与L2、L3反向时:
证明:当n为偶数且L的3个分支L1,L2,L3同向时,
,
,
,将各参数代入
得:
当n为偶数且L的三个分支分别为L1与L2同向,L3与L1、L2反向;L1与L3同向,L2与L1、L3反向;L2与L3同向,L1与L2、L3反向时,
,
,
,将各参数代入
得:
4. 结语
本文主要研究了一类花图
的Tutte多项式,根据Tutte多项式与Jones多项式之间的关系讨论了参数
、
、
在不同情况下的变化规律,最后计算得到对应于各边均为正号的花图
的链环L的Jones多项式。