基于投影策略的改进在线非线性分类算法

Improved Online Nonlinear Classification Algorithm Based on Projection Strategy

摘要: 在线学习自提出以来已经发展出许多算法及其改进，根据模型是线性还是非线性，将在线学习算法分为两大类：在线线性学习算法和基于核的在线学习算法。核方法是指利用特征映射，将样本映射到高维再生核希尔伯特空间，从而将线性不可分问题转化成线性可分问题。并行投影算法是用自适应投影次梯度方法(APSM)推导的，其优点是收敛速度快，但该算法的稀疏方式是当模型的规模达到一定容量时，可能将最远端某些重要的数据点删除，从而导致算法性能严重退化；以及存在偏移量使得分类效果变差。为了改进以上问题，本文是在并行投影算法的基础上提出了一种新的算法，其稀疏方式是利用最新的数据向字典中的数据做投影，从而在保证误分类率低时，本文算法的字典规模较小。仿真数据和真实数据的实验结果表明，与其他七种经典在线分类算法相比，本文算法在字典规模较小时，误分类率最低。

Abstract: Online learning has developed many algorithms and their improvements since it was proposed. According to whether the model is linear or nonlinear, online learning algorithms are divided into two categories: online linear learning algorithms and kernel-based online learning algorithms. The kernel method is to map the sample to a high-dimensional regenerated kernel Hilbert space by us-ing feature mapping, so that the linear indivisible problem can be transformed into a linear separa-ble problem. The parallel projection algorithm is derived by the adaptive projection subgradient method (APSM), which has the advantage of fast convergence, but the sparse way of the algorithm is that when the scale of the model reaches a certain capacity, some important data points at the far-thest end may be deleted, resulting in serious degradation of the algorithm performance. And the existence of offset makes the classification effect worse. In order to improve the above problems, this paper proposes a new algorithm based on the parallel projection algorithm. Its sparse method is to use the latest data to project the data in the dictionary, so that the dictionary size of the algo-rithm in this paper is small when the classification error rate is low. The experimental results of simulation data and real data show that compared with other online algorithms, the proposed algo-rithm has the lowest classification error rate when the dictionary size is small.

1. 引言

机器学习算法分为批处理算法和在线学习算法，批处理算法可以一次性批量输入给学习算法，并在小规模数据上取得了巨大成功，但当数据规模较大时，批处理算法的计算复杂度高，并且不适合动态变化的环境。与批处理算法相比，在线学习算法适用于大规模数据和动态环境，并且能够降低学习算法的空间复杂度和时间复杂度。在大数据时代，数据高速增长的特点为机器学习带来了更加严峻的挑战，而在线学习算法可以有效地解决该问题，因此引起了人们的广泛关注。

设计良好的在线学习算法只需较少的计算，就能达到与批处理算法相同的效果。在线学习算法可以分为在线线性学习算法和基于核的在线学习算法，当样本线性可分时，在线线性学习算法可以有效分类，而在基于核的在线学习算法中，由于样本线性不可分，常需要利用特征映射，将样本映射到高维再生核希尔伯特空间，从而将线性不可分问题转化成线性可分问题，来降低分类任务的难度。在过去几年中，开发了很多基于核的在线学习算法，并在很多问题上也展现了很好的性能。

1958年，Rosenblatt首次提出了感知机(Perceptron)算法，并证明了对于线性可分问题，该算法总是收敛的 [1] 。文献 [2] 基于核的感知机算法，其主要思想是通过特征映射将非线性分类问题转化成特征空间的线性问题，并在特征空间应用感知机算法求解。2004年，J.Kivinen等人提出了核最小均方算法 [3] 。Engel等人提出了核递归最小二乘算法，由Mercer核诱导的高维特征空间中执行线性回归，因此可以用于递归地构造非线性最小二乘问题的最小均方误差解，并且首次将核方法扩展到自适应滤波 [4] 。2004年，Isao Yamada和Nobuhiko Ogura首次提出自适应投影次梯度方法，该算法是把分类问题转化为一个凸优化问题 [5] 。2008年，Konstantinos Slavakis等人引入了自适应投影次梯度法，利用基于投影的自适应滤波工具，导出一种新的用于再生核希尔伯特空间(RKHS)分类的在线算法 [6] 。

本文是在文献 [6] 中并行投影算法的基础上进行改进，而并行投影算法具有收敛速度快的优点，但是也存在缺点。第一，由于并行投影算法存在偏移量，会导致分类效果差；第二，并行投影算法的稀疏方式是当样本容量小于预设的预算时，数据点将会进入字典；当样本容量大于预设的预算时，将最远端的数据点删除，而该数据点可能是最重要的数据点，从而导致算法性能严重退化。

基于核的在线学习算法面临的问题是随着训练次数的增加，导致模型的规模随之增大，需要的计算量和存储空间也越来越多，为了改善以上缺点，需要对模型进行稀疏处理。在算法中加入稀疏处理，能够有效地改变字典规模的大小。因此，本文提出了新的算法：基于投影策略的改进在线非线性分类算法，本文的算法在误分类率(misclassification rate)和字典规模方面都具有一定的优势。

为了更清楚地表述，本文用 $Z$ ， $Z_{\ge 0}$ ， $Z_{>0}$ ， $ℝ$ 表示所有整数，非负整数，正整数和实数。此外，对于任意整数 $j_1\le j_2$ ，定义 $\overline{j_1,j_2}:=\left\{j_1,j_1+1,\cdots ,j_2\right\}$ 。

2. 问题描述

考虑一个在线二元分类问题，假设 ${\left(x_t\right)}_{t\in Z_{\ge 0}}\in \mathcal{X}$ 为输入向量序列，其中 $\mathcal{X}\in {ℝ}^m$ 为输入向量集合。用给

出的数据对 $\left(x_t,y_t\right)$ ，训练一个非线性分类器 $f:{ℝ}^d\to ℝ$ ，其中t表示第t轮，d是维数， $y_t\in \left\{+1,-1\right\}$ 是真实的类别标签。

对于在线分类问题，可以通过最小化软边际损失函数 $l(\cdot ):\mathcal{H}\to ℝ$ 来训练分类器 $f\in \mathcal{H}$ ：

$l\left(\left(x_t,y_t\right);f\right)=\max \left(0,\rho -y_{t}f\left(x_t\right)\right)$ ,

其中 $\rho$ 为边缘参数。

在线非线性的分类算法在特征空间 $\mathcal{H}$ 中形成分类器(点)的形式为

$f:={\displaystyle \underset{t=0}{\overset{\infty }{\sum }}{\alpha }_t}k\left(x_t,\cdot \right)\in \mathcal{H}$ .

基于核的在线学习算法的目的是学习关于核的预测模型 $f\left(x\right)$ ，用于如下分类新数据点 $x\in {ℝ}^d$ ：

$f\left(x\right)={\displaystyle \underset{t=1}{\overset{T}{\sum }}{\alpha }_t}k\left(x_t,x\right)$ ,

其中T为处理数据点的数量， ${\alpha }_t$ 表示第t个数据点的系数， $k\left(\cdot ,\cdot \right)$ 表示核函数。

本文的目的是在并行投影算法的基础上进行更新，下面小节将给出本文算法。

3. 本文算法

在本文中，主要讨论了基于投影策略的改进在线非线性分类算法。第一部分介绍了基于并行投影的在线分类算法的推导，第二部分介绍了算法的稀疏。

3.1. 基于并行投影的在线分类算法的推导

本节主要利用文献 [6] 中并行投影算法的推导，下面将简单的介绍一下并行投影算法的推导过程。

$\forall t\in Z_{>0}$ ，每个点的索引集 $J_t\subset \overline{0,t}$ ，对于 $j\in J_t$ 有闭半空间

.

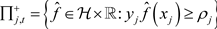给定分类器 $u_t\in \mathcal{H}$ ，任意函数 $u\in \mathcal{H}$ ，定义函数列为

${\Theta }_t\left(u\right)=\{\begin{array}{l}{\displaystyle \underset{j\in J_t}{\sum }\frac{w_{j}d\left(u_t,{\prod }_{j,t}^{+}\right)}{L_t}d}\left(u,{\prod }_{j,t}^{+}\right),L_t\ne 0\\ 0,L_t=0\end{array}$ ,

其中 $L_t:={\displaystyle \underset{j\in J_t}{\sum }{w}_{j}d\left(u_t,{\prod }_{j,t}^{+}\right)}$ ，权重 $w_j\ge 0$ ， $\forall j\in J_t$ 且 ${\displaystyle \underset{j\in J_t}{\sum }{w}_j=1}$ 。

根据距离公式 $d\left(f,c\right)=\Vert f-P_c\left(f\right)\Vert$ ，其中点 $f\in \mathcal{H}$ ，闭凸集 $c\subset \mathcal{H}$ ， $P_c\left(f\right)$ 表示f向c投影，可知

$d\left(u,{\prod }_{j,t}^{+}\right)=\Vert u-P_{{\prod }_{j,t}^{+}}\left(u\right)\Vert$ .

把 $u_t$ 代入 ${\Theta }_t\left(u\right)$ 中，可得

${\Theta }_t\left(u_t\right)=\frac{1}{L_t}{\displaystyle \underset{j\in J_t}{\sum }{w}_j{d}^2\left(u_t,{\prod }_{j,t}^{+}\right)}$ .

该函数 ${\left\{d\left(\cdot ,{\prod }_{j,t}^{+}\right)\right\}}_{j\in J_t}$ 是闭凸集的度量距离函数，是连续的和次可微的。

对 $d\left(u,{\prod }_{j,t}^{+}\right)$ 求次梯度，可知

$\partial d\left(u,{\prod }_{j,t}^{+}\right)=\left\{\frac{u-P_{{\prod }_{j,t}^{+}}\left(u\right)}{d\left(u,{\prod }_{j,t}^{+}\right)}\right\}=\frac{u-P_{{\prod }_{j,t}^{+}}\left(u\right)}{\Vert u-P_{{\prod }_{j,t}^{+}}\left(u\right)\Vert }$ .

对 ${\Theta }_t\left(u_t\right)$ 求导知

${{\Theta }^{\prime }}_t\left(u_t\right)=\frac{1}{L_t}{\displaystyle \underset{j\in J_t}{\sum }{w}_{j}d\left(u_t,{\prod }_{j,t}^{+}\right)}\frac{u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)}{\Vert u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\Vert }$ .

因为 $d\left(u_t,{\prod }_{j,t}^{+}\right)=\Vert u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\Vert$ ，所以有

${{\Theta }^{\prime }}_t\left(u_t\right)=\frac{1}{L_t}{\displaystyle \underset{j\in J_t}{\sum }{w}_j\left(u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\right)}$ , (1)

由APSM算法的迭代公式可知

$u_{t+1}=u_t-{\lambda }_t\frac{{\Theta }_t\left(u_t\right)}{{\Vert {{\Theta }^{\prime }}_t\left(u_t\right)\Vert }^2}{{\Theta }^{\prime }}_t\left(u_t\right)$ .

将(1)式代入APSM算法的迭代公式中，可知

$u_{t+1}=u_t-{\lambda }_t\frac{{\displaystyle \underset{j\in J_t}{\sum }{w}_j{d}^2\left(u_t,{\prod }_{j,t}^{+}\right)}}{{\Vert {\displaystyle \underset{j\in J_t}{\sum }{w}_j\left(u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\right)}\Vert }^2}{\displaystyle \underset{j\in J_t}{\sum }{w}_j\left(u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\right)}$ .

令

${\mu }_t={\lambda }_t\frac{{\displaystyle \underset{j\in J_t}{\sum }{w}_j{d}^2\left(u_t,{\prod }_{j,t}^{+}\right)}}{{\Vert {\displaystyle \underset{j\in J_t}{\sum }{w}_j\left(u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\right)}\Vert }^2}$ ,

故

$u_{t+1}=u_t-{\mu }_t{\displaystyle \underset{j\in J_t}{\sum }{w}_j\left(u_t-P_{{\prod }_{j,t}^{+}}\left(u_t\right)\right)}$ . (2)

令

${\beta }_j=w_j\cdot y_j{\left(\rho -y_j{f}_t\left(x_j\right)\right)}^{+}$ .

则算法过程中(2)式可以等价地写为

$f_{t+1}=f_t+{\mu }_t{\displaystyle \underset{j\in J_t}{\sum }{\beta }_{j}k\left(x_j,\cdot \right)}$ . (3)

3.2. 算法的稀疏

随着训练次数的增加，会导致利用(3)式更新的算法中的字典规模越来越大，因此人们引入了各种在线稀疏方法，例如滑动窗技术 [6] 、贪婪法 [7] 、随机法 [8] 、量化法 [9] 等等。在本节中，当最新的数据可以利用字典中的元素近似表示时，最新的数据将不进入字典，此时需要用最新的数据向字典中的数据做投影，利用求矩阵的逆的方法进行更新；否则，最新的数据将进入字典。

设 ${\left(x_t\right)}_{t\in z_{\ge 0}}\in \mathcal{X}$ 为输入向量序列，其中 $\mathcal{X}\in {ℝ}^m$ 为输入向量集合， $y_t\in \left\{+1,-1\right\}$ 为标签。在 $t-1$ 时刻，字典为 $D_{t-1}={\left\{{\tilde{x}}_j\right\}}_{j=1}^{m_{t-1}}$ 。当获得最新数据 $x_t$ 时，本文算法需要判断是否满足近似线性相关(ALD)条件

${\delta }_t=\underset{a}{\min }{\Vert {\displaystyle \underset{j=1}{\overset{m_{t-1}}{\sum }}{a}_j\Phi \left({\tilde{x}}_j\right)-\Phi \left(x_t\right)}\Vert }^2\le \eta$ ,

即将最新数据 $\Phi \left(x_t\right)$ 向字典 $D_{t-1}$ 做投影，其中投影系数为

$a_t={\tilde{K}}_{t-1}^{-1}{\tilde{k}}_{t-1}\left(x_t\right)$ . (4)

若最新数据 $x_t$ 满足ALD条件，即投影误差 $\Vert {\delta }_t\Vert$ 小于给定的阈值 $\eta$ ，因此可以利用字典中已有的元素近似表示，所以最新的数据将不进入字典；若最新数据 $x_t$ 不满足ALD条件，即投影误差 $\Vert {\delta }_t\Vert$ 大于给定的阈值 $\eta$ ，因此最新数据不能利用字典中的元素近似表示，会导致很大的误差，所以最新数据进入字典。

无论数据是否进入字典，都需要将数据向字典做投影，从而得到每个投影系数，将所有展开的投影系数组成系数矩阵，本节的系数矩阵是由最新的q个数据向字典做投影，可以得到最新q个数据展开的投影系数，然后将其组成系数矩阵，用 $A_t$ 表示

$A_t=\left[\begin{array}{c}{a}_{t-q+1}^{\text{T}}\\ a_{t-q+2}^{\text{T}}\\ ⋮\\ a_t^{\text{T}}\end{array}\right]$ .

在下一次迭代时，因为不再考虑 $k\left(x_{t-q+1},\cdot \right)$ ，所以不再考虑 $k\left(x_{t-q+1},\cdot \right)$ 在字典 $D_{t-1}$ 上的投影，因此引入矩阵

${\bar{A}}_{t-1}=\left[\begin{array}{c}{a}_{t-q+2}^{\text{T}}\\ ⋮\\ a_{t-1}^{\text{T}}\end{array}\right]$ .

故(3)式中 ${\displaystyle \underset{j\in J_t}{\sum }{\beta }_j}k\left(x_j,\cdot \right)$ 可写成如下形式

${\displaystyle \underset{j\in J_t}{\sum }{\beta }_j}k\left(x_j,\cdot \right)\approx \left({\beta }_{t-q+1},{\beta }_{t-q+2},\cdots ,{\beta }_t\right)A_t\left(\begin{array}{c}k\left(x_{t-q+1},\cdot \right)\\ k\left(x_{t-q+2},\cdot \right)\\ ⋮\\ k\left(x_t,\cdot \right)\end{array}\right)$ .

下面将分情况讨论最新数据是否进入字典，投影系数、字典和字典维数分别是如何更新的。

当 $\Vert {\delta }_t\Vert >\eta$ 时，数据 $k\left(x_t,\cdot \right)$ 不能利用字典中的元素所表示，会导致很大的误差，因此数据 $k\left(x_t,\cdot \right)$ 要向自己做投影，可以得到其投影系数为 $a_t=\left(0,0,\cdots ,1\right)$ ，所以矩阵 $A_t$ 的更新为 $A_t=\left[\begin{array}{cc}{\bar{A}}_{t-1}& 0\\ 0& 1\end{array}\right]$ ，系数更新为 ${{\Upsilon }^{\prime }}_t=\left[\begin{array}{cc}{\Upsilon }_{t-1}& 0\end{array}\right]$ ， ${\Upsilon }_t={{\Upsilon }^{\prime }}_t+{\beta }_t{A}_t$ 。此时，最新数据将进入字典，字典的更新为 $D_t=D_{t-1}\cup \left\{x_t\right\}$ ，字典维数更新为 $m_t=m_{t-1}+1$ 。

当 $\Vert {\delta }_t\Vert \le \eta$ 时，数据 $k\left(x_t,\cdot \right)$ 可以利用已有字典中的元素表示，因此数据 $k\left(x_t,\cdot \right)$ 要向字典 $D_{t-1}$ 做投影，得到其投影系数为 $a_t={\tilde{K}}_{t-1}^{-1}{\tilde{k}}_{t-1}\left(x_t\right)$ ，所以矩阵 $A_t$ 的更新为 $A_t=\left[\begin{array}{c}{\bar{A}}_{t-1}\\ a_t^{\text{T}}\end{array}\right]$ ，系数更新为 ${{\Upsilon }^{\prime }}_t={\Upsilon }_{t-1}$ ， ${\Upsilon }_t={{\Upsilon }^{\prime }}_t+{\beta }_t{A}_t$ 。此时，最新数据不会进入字典，字典不变，字典更新为 $D_t=D_{t-1}$ ，字典维数更新为 $m_t=m_{t-1}$ 。

综上，引入稀疏化环节后，本文的更新公式为

$f_t(\cdot )={\displaystyle \underset{j=1}{\overset{m_t}{\sum }}{\Upsilon }_t\left(j\right)k\left(x_j,\cdot \right)}$ .

至此，本文得到了新算法，新算法的伪代码如下。

4. 实验结果

在本节中，新算法与其他不同算法分别在仿真数据和真实数据下进行性能比较，并将算法参数的设置以表格的形式展示，各个算法的误分类率和字典维数以图的形式展示。由于误分类率可以作为衡量不同算法性能的重要指标，在下面的仿真数据实验中，利用测试集上的误分类率来衡量不同算法的性能，其定义式如下：

$误分类率=\frac{{\displaystyle \underset{i}{\sum }I\left(y_i\ne {\hat{y}}_i\right)}}{n}$ ,

上式中n表示测试数据集的长度， $y_i$ 表示i时刻的期望输出， ${\hat{y}}_i$ 表示i时刻对测试数据的实际输出。

4.1. 仿真数据比较

本文使用的仿真数据与文献 [6] 相同，其中输入数据对 $\left(x_t,y_t\right)$ ， $x_t\in {ℝ}^4$ ， $y_t\in \left\{+1,-1\right\}$ 。为了算法比较的公平性，本文算法与APSM算法 [6] ，SPA算法 [10] ，Perceptron算法 [2] ，OLRU算法 [11] ，OLRD算法 [11] ，Projectron算法 [12] ，Projectron++算法 [12] 等算法进行性能对比，对比的算法都具有良好的鲁棒性，具体的参数选择在下面表1中说明。

Table 1. Parameter setting of each algorithm

表1. 各个算法的参数设置

根据上述参数的设置，本文算法与各个算法进行比较，下图展示各个算法的误分类率及字典维数D。

图1显示，本文提出的算法比其他算法相比，在字典规模较小时，本文提出的算法的误分类率最低。

4.2. 真实数据比较

真实数据集是来自LIBSVM数据存储库的二分类数据集，其中LIBSVM是一个支持向量机的库，它由台湾大学(Taiwan University)的林智仁(Chih-Jen Lin) 教授和他的团队所开发的。该库提供了一种简单且高效的方式，用于解决回归(regression)、分类(classification)和分布估计(distribution estimation)等问题。

下面在真实数据a3a以及a7a的各个算法进行性能比较，其中两组数据的参数相同，都用了以下表2参数的设置。为了算法比较的公平性，选择对比的算法都具有良好的鲁棒性，具体的参数选择在下面表2中说明。

Figure 1. The performance of the proposed algorithm is compared with other algorithms under simulation data

图1. 本文算法和其他算法在仿真数据下的性能比较

Table 2. Parameter setting of each algorithm

表2. 各个算法的参数设置

根据上述参数的设置，将各个算法与本文提出的算法分别在a3a以及a7a数据中，进行了比较，下图给出各个算法的误分类率以及字典维数D。

图2运用的数据是a3a，测试数据为20,000个，训练数据为3000个，核长均为1。在a3a数据中，本文提出的算法与其他算法相比，新算法在字典规模较小时，误分类率最低。

图3运用的数据是a7a，测试数据为16,000个，训练数据为10,000个，核长均为1。在a7a数据中，这八种算法是在期望的参数下进行的对比，本文提出的算法与其他算法相比，新算法在字典规模较小时，误分类率最低。

Figure 2. Performance comparison of the proposed algorithm and other algorithms under a3a data

图2. 本文算法和其他算法在a3a数据下的性能比较

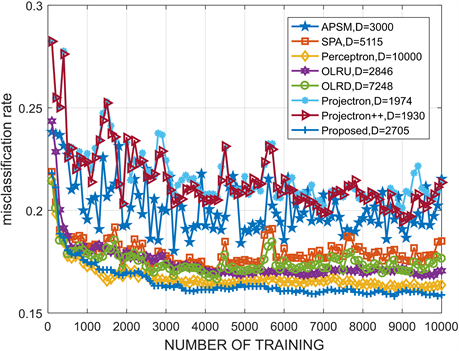
Figure 3. Performance comparison of the proposed algorithm and other algorithms under a7a data

图3. 本文算法和其他算法在a7a数据下的性能比较

5. 总结

基于核的在线学习算法面临的问题是随着训练次数的增加，导致模型的规模随之增大，需要的计算量和存储空间也越来越多，为了改善以上缺点，需要对模型进行稀疏处理。本文是在并行投影算法的基础上提出了一种新的算法为基于投影策略的改进在线非线性分类算法，其稀疏方式是最新的数据要向字典中的数据做投影。字典维数是否增加，和投影误差有关。当投影误差大于阈值时，新数据进入字典，字典维数增加；反之，小于阈值时，新数据不进入字典，新的系数可以用字典中原有的系数和基底近似表示，字典维数不变。仿真数据和真实数据的实验结果表明，与其他七种经典的在线分类算法相比，本文算法在字典规模较小时，误分类率最低。

基金项目

辽宁省自然科学基金(项目编号2019-ZD-0106，2019-ZD-0087)。

NOTES

^*通讯作者。