支撑物对全钢化真空玻璃的抗冲击性能模拟研究

Research on Impact Resistance of Pillars to Fully Tempered Vacuum Glass

摘要: 全钢化真空玻璃因其具备优异的隔声、节能、安全性能而被人们广泛关注，但其抗冲击性能及其冲击失效形式有待人们进一步深入研究。通过ANSYS仿真平台建立落球冲击全钢化真空玻璃的显示动力学模型并进行冲击仿真，研究相同间距下不同支撑物类型和支撑物不同排布方式下落球冲击全钢化真空玻璃的抗冲击性能。结果表明采用环型支撑物的全钢化真空玻璃抗冲击性能最好，采用圆球型支撑物的全钢化真空玻璃抗冲击性能最差；支撑物呈正三角形排布的全钢化真空玻璃的抗冲击性能最好，支撑物呈正六边形排布的全钢化真空玻璃的抗冲击性能最差。

Abstract: Fully tempered vacuum glass has been widely concerned for its excellent sound insulation, energy saving and safety performance, but its impact resistance and impact failure mode need to be fur-ther studied. Through ANSYS simulation platform, the display dynamics model of falling ball impact on fully tempered vacuum glass was established and impact simulation was carried out to study the impact resistance of falling ball impact on fully tempered vacuum glass with different types of pil-lars and different layouts of pillars at the same distance. The results show that the impact re-sistance of fully tempered vacuum glass with ring type pillar is the best, and the impact resistance of fully tempered vacuum glass with round ball type pillar is the worst. The impact resistance of fully tempered vacuum glass with triangular arrangement of pillar is the best, and the impact re-sistance of fully tempered vacuum glass with hexagonal arrangement of pillar is the worst.

1. 引言

玻璃在钢化后其表面形成正压力层，使其强度大大提高，对比同等厚度的普通玻璃，钢化玻璃的抗弯强度提升了2~3倍，抗冲击性能提升了2~4倍，而且其破碎后的碎片小，无锐角，大大提高了其安全性能 [1] [2] [3] 。全钢化真空玻璃是新一代真空玻璃，它不仅具有真空玻璃隔声降噪、保温节能等优异性能，更具备良好的力学性能，属于安全玻璃的一种 [4] [5] 。

国内外诸多学者对玻璃的抗冲击性能进行了研究。缪宏等 [6] 通过试验发现随着激振器发出激振力频率的不断增加，真空平板玻璃的动态响应呈现先增大后减小的趋势，并在50 Hz的时候出现共振现象，动态响应达到峰值。高帅等 [7] 通过钢化真空玻璃落球仿真发现，冲击点在支撑物附近，钢化真空玻璃的冲击失效概率最大；冲击点在2个支撑物中间部位，钢化真空玻璃的冲击失效概率最小。王木飞等 [8] 通过分别采用单元删除法、DG-PD和M-PD三种方法研究平板玻璃冲击作用下的裂纹扩展规律。朱禹翰等 [9] 通过对81组物理钢化玻璃进行碎裂试验，对最终裂纹损伤模态进行统计分析，并结合Voronoi形态方法对钢化玻璃的裂纹形态进行表征。然而，在研究真空玻璃抗冲击性能的影响因素时，支撑物类型对抗冲击性能影响的研究却很少。在钢化真空玻璃的实际应用中，选用较好的支撑物类型，能提高其产品的吸收能，提高抗冲击性能。在全钢化真空玻璃的推广应用方面，一定程度上对建筑安全性能起到了积极作用。

2. 全钢化真空玻璃冲击理论

全钢化真空玻璃是一种弹脆性材料，在施加应力达到材料极限之前，构件表现为优良的弹性体，但当施加的应力达到弹性极限时，材料会出现裂纹，并迅速扩展，瞬间分裂为小块、无锐角的碎片。在此研究中假设全钢化真空玻璃是理想弹性体，并且默认当应力超过105 MPa时及认定全钢化玻璃已经失效 [10] 。

当全钢化真空玻璃某个地方受到钢球冲击力的扰动，会使该处的应力迅速升高，与周围其他地方产生应力差，此时构件处于一种力学上的不平衡状态，然后该处应力会由近及远以波的形式传播出去该处的扰动，传播过程中常常伴随着反射、透射、叠加和消散等现象，最终使整个构件都承受该扰动的影响，并努力快速地恢复原有的状态 [11] 。弹性波在不同介质界面的反射和透射如图1所示。

入射波强度：

${\sigma }_i={\sigma }_1-{\sigma }_0=-{\left({\rho }_0{c}_0\right)}_{玻}\left(v_1-v_0\right)=-{\left({\rho }_0{c}_0\right)}_{玻}{v}_i$ (1)

透射波强度：

${\sigma }_t={\sigma }_2-{\sigma }_0=-{\left({\rho }_0{c}_0\right)}_{玻}\left(v_2-v_0\right)=-{\left({\rho }_0{c}_0\right)}_{玻}{v}_t$ (2)

反射波强度：

${\sigma }_r={\sigma }_2-{\sigma }_1={\left({\rho }_0{c}_0\right)}_{玻}\left(v_1-v_2\right)={\left({\rho }_0{c}_0\right)}_{玻}{v}_r$ (3)

式中， ${\rho }_0$ 为密度， $c_0$ 为纵波速度， ${\rho }_0{c}_0$ 为介质的波阻抗， $v_i$ 为入射波速度， $v_r$ 为反射波速度， $v_t=v_i+v_r$ 为透射波速度。

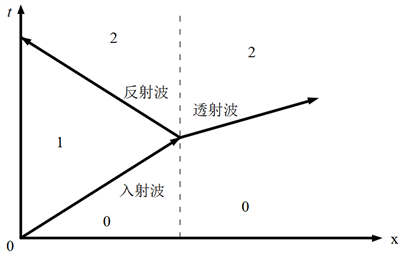
Figure 1. Transmission and reflection of elastic waves at different interfaces

图1. 弹性波在不同界面的透射和反射

3. 全钢化真空玻璃动力学模型

为方便有限元仿真的计算和与现实情况的吻合，需要对全钢化真空玻璃进行以下几种假设：(1) 弹性体假设：全钢化玻璃是弹脆性材料，在未超过其弹性极限时默认全钢化真空玻璃为理想的弹性体；(2) 边界无位移，现实使用情况下，全钢化真空玻璃的边界是被完全固定的，因此仿真时将四周进行完全约束；(3) 刚体假设，由于支撑物的弹性模量远大于全钢化玻璃的弹性模量，故设定支撑物为刚体。

建立落球冲击全钢化真空玻璃的物理模型(5 + 0.3V + 5)，如图2所示，全钢化玻璃基片长、宽、厚分别为500、500、5 mm。封接层的宽度为7 mm，真空层0.3 mm。本研究相邻支撑物的间距都是50 mm，支撑物的厚度都是0.3 mm，图中的支撑物排布方式为50 mm × 50 mm的正方形排布。根据《建筑用安全玻璃第2部分：钢化玻璃》(GB15763.2-2005) [12] 中的要求，采用表面光滑的钢球，直径为63.5 mm，质量约为1040 g，落球点在构件的中心位置附近。本文控制落球、全钢化玻璃基片、封接层的参数不变，改变的仅为支撑物类型和支撑物的排列方式。

Figure 2. Schematic diagram of the explosion of a fully tempered vacuum glass on impact of a falling ball

图2. 落球冲击全钢化真空玻璃爆炸示意图

封接层的材料是一种特质材料，其主要成分为Sn3.5Ag，支撑物材料均为304不锈钢，钢球的材料是结构钢。落球冲击全钢化真空玻璃结构中的材料参数如表1所示。

Table 1. Material attribute

表1. 材料属性

支撑物的存在必定会影响人眼的对窗外景观的观感，这是真空玻璃无法规避的“缺陷”。支撑物的直径和高度要尽可能的小，使得肉眼在距离一定距离时的不同角度都无法分辨。本文所选的支撑物高度都是0.3 mm，宽度也都不超过0.6 mm，人在1 m距离观看时，如图3所示，人眼的视角不超过0.04˚，远小于人眼可分辨的视角0.1˚~1˚ [13] ，此时透过玻璃观察外部景观就不受支撑物的影响。

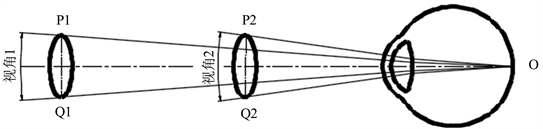
Figure 3. Schematic diagram of the viewing angle of the support object observed by human eyes

图3. 人眼观察支撑物的视角示意图

冲击点在全钢化真空玻璃的不同位置的失效概率和所受最大应力值存在特别大的差异，特别是冲击点在支撑物附近产生的应力会明显偏大，失效概率显著提高。本研究所选的冲击点为最靠近全钢化真空玻璃的最中间的支撑物单元的中心，也就是正方形的中心、正三角形的重心，正六边形的中心。

4. 不同支撑物类型下落球冲击全钢化真空玻璃数值模拟

4.1. 支撑物类型

本文分析的支撑物类型有圆柱型、空心圆柱型、圆球型、圆环型和C型 [14] 。这五种支撑物都是常用的支撑物，它们的形状特征如图4所示。

针对支撑物类型对全钢化真空玻璃的抗冲击性能的影响，设置了五组仿真方案，如表2所示。本次限定落球在0.5 m高度自由下落，及设定落球碰撞全钢化真空玻璃的初速度为3.13 m/s。

Table 2. Steel ball impact fully tempered vacuum glass simulation program information

表2. 钢球冲击全钢化真空玻璃仿真各方案信息

Figure 4. Five common types of pillars

图4. 五种支撑物的常用类型

4.2. 落球冲击全钢化真空玻璃应力波传播过程

落球冲击圆柱型支撑物的全钢化真空玻璃具体的应力传播过程如图5所示，其他支撑物类型下的全钢化真空玻璃被落球冲击的应力传播过程的应力云图也与其大致相同，应力云图本文就不再详细展示。钢化真空玻璃在受大气压的作用下，支撑物处产生应力集中。当钢球冲击全钢化真空玻璃时，冲击点处瞬间产生应力，并以冲击点为中心开始向四周传播应力。由于支撑物的存在，应力波在到达每一个支撑物的位置都会发生变化，应力波在支撑物处会发生反射、折射、叠加等现象，同时最重要的是，应力波会在支撑物附近产生应力集中的现象。冲击点的应力波会快速地向四周传播，在1.25 ms以后应力波会到达玻璃的边界。支撑物处受到冲击点传播来的应力波，会出现应力集中，并以支撑物为中心开始向四周传播。支撑物处产生的应力波会与冲击点处产生的应力波相互叠加或相互抵消，各个支撑物产生的应力波也会相互叠加或抵消。构件受到的最大应力值会迅速上升到一个最大值，然后会逐渐缓慢的减小到仅受大气压强时构件受到的最大应力值。以0.25 ms作为一个节拍，展示构件五个节拍的节点的应力分布图。在0.75 ms左右，构件受到的应力将达到最大值(应力波辐射到最近几个支撑物处，经过不停息的反射、折射、叠加，并且支撑物相对于钢化玻璃为刚体而产生应力集中，迅速累积使得应力达到了最大值)，最大应力值也是判定全钢化真空玻璃是否已经失效的决定性指标，当最大应力超过105 MPa，即全钢化真空玻璃已经失效。

(a) 0.25 ms (b) 0.5 ms (c) 0.75 ms (d) 1 ms (e) 1.25 ms (f) 1.5 ms

Figure 5. Stress propagation of fully tempered vacuum glass for cylindrical pillars

图5. 圆柱型支撑物的全钢化真空玻璃的应力传播

4.3. 数值模拟结果与分析

通过仿真，得到五种支撑物类型下，全钢化真空玻璃受到钢球冲击时的最大应力云图，如图6所示。

(a) 圆柱型 (b) 空心圆柱形 (c) 圆球型(d) 圆环型 (e) C型

Figure 6. Nephogram of the maximum stress of five kinds of pillars falling ball impact members

图6. 五种支撑物落球冲击构件最大应力云图

结果表明，采用五种支撑物的全钢化真空玻璃的抗冲击性能由强到弱依次是圆环型、空心圆柱型、C型、圆柱型、圆球型。在落球都在0.5 m高度自由落体冲击构件时，既保证仿真时落球的末速度都是3.13 m/s (根据公式 $v_{末}^2-v_{初}^2=2gh$ ，g取9.8 m/s²)的情况下，环型支撑物的全钢化真空玻璃受到的最大应力最小为87.456 MPa，圆球型支撑物的全钢化真空玻璃受到的最大应力最大为125.19 MPa。在保证除支撑物外其他条件相同的情况下，受到的最大应力越大，说明该构件的抗冲击性能越差；反之，受到的最大应力越小，说明该构件的抗冲击性能越好。圆球型支撑物与玻璃基片之间是点接触集中应力最大，空心圆柱型、C型、圆柱型与玻璃基片之间是面接触集中应力次之，圆环型与玻璃基片之间是光滑圆面与平面的切线接触集中应力最小，二者之间的接触没尖角、缺口、沟槽等缺陷故应力集中很小。空心圆柱型、C型相对于圆柱型都有多余空隙，应力波的叠加会有短暂的停歇，并且会产生发散作用而使其最大应力变小。C型相对于空心圆柱形尖角较多，易产生应力集中。

5. 不同排布方式下落球冲击全钢化真空玻璃数值模拟

5.1. 支撑物排列类型

支撑物的排布方式主要有正方形排布、正三角形排布和正六边形排布三种排布方式 [15] 。本文所研究的全钢化玻璃是300 mm × 300 mm的基片，支撑物的间距都是50 mm，前文已经提到支撑物选用环型的全钢化真空玻璃的抗冲击性能最好，所以本段我们都选用环形支撑物作为研究对象。三种排布方式的具体形式如图7所示。

Figure 7. Schematic diagram of support point arrangement

图7. 支撑点排列方式示意图

5.2. 数值模拟结果与分析

前文已经说明当构件受到的最大应力超过105 MPa，就认定构件应经发生失效。落球的高度越高，冲击构件的末速度越大，冲击能量越大，构件受到的最大应力也越大，因此当落球达到某个高度自由落体冲击构件，构件会发生失效。通过仿真尝试发现三种不同排列方式发生失效时的落球的高度。

由图8可知，支撑物为正方形排布的全钢化真空玻璃在落球高度为0.59 m、0.60 m、0.61 m的最大应力分别为102.2 MPa、103.79 MPa、105.69 MPa。全钢化玻璃基片在落球高度为0.61 m时受到的最大应力超过105 MPa会发生失效，故正方形排布的全钢化真空玻璃的承受极限为0.60 m的落球自由落体冲击。

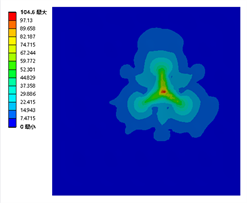
由图9可知，支撑物为正三角形排布的全钢化真空玻璃在落球高度为0.65 m、0.66 m、0.67 m的最大应力分别为103.34 MPa、104.6 MPa、106.02 MPa。全钢化玻璃基片在落球高度为0.67 m时受到的最大应力超过105 MPa会发生失效。故正三角形排布的全钢化真空玻璃的承受极限为0.66 m的落球自由落体冲击。

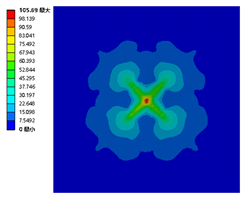
(a) 0.59 m (b) 0.60 m (c) 0.61 m

Figure 8. Maximum stress nephogram of a square arrangement of falling ball impact member

图8. 正方形排布落球冲击构件的最大应力云图

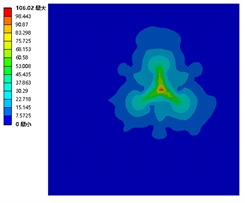
(a) 0.65 m (b) 0.66 m (c) 0.67 m

Figure 9. Nephogram of the maximum stress of an equilateral triangle arrangement of a falling ball impact member

图9. 正三角形排布落球冲击构件的最大应力云图

(a) 0.52 m (b) 0.53 m (c) 0.54 m

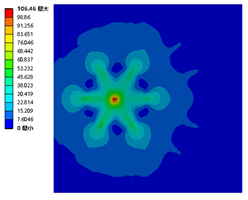
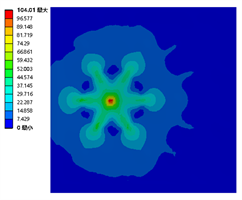
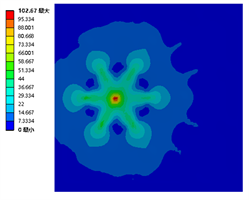
Figure 10. Maximum stress nephogram of a falling ball impact member with regular hexagon arrangement

图10. 正六边形排布下落球冲击构件的最大应力云图

由图10可知，支撑物为正六边形排布的全钢化真空玻璃在落球高度为0.52 m、0.53 m、0.54 m的最大应力分别为102.67 MPa、104.01 MPa、106.46 MPa。全钢化玻璃基片在落球高度为0.54 m时受到的最大应力超过105 MPa会发生失效。故正六边形排布的全钢化真空玻璃的承受极限为0.53 m的落球自由落体冲击。

通过对比我们发现支撑物为正三角形排布的全钢化真空玻璃的抗冲击性能最好，支撑物为正六边形排布的全钢化真空玻璃的抗冲击性能最差。

在全钢化真空玻璃的实际生产制造过程中，上述仿真结果对选择优化全钢化真空玻璃的抗冲击性能具有一定的指导意义。

6. 结论

(1) 在钢球冲击全钢化真空玻璃的过程中，冲击力以应力波的形式从冲击点为中心向四周传播，应力波在支撑物处会产生应力集中并向四周传播，支撑物辐射的应力波会与冲击点的应力波产生叠加现象，也会与其他支撑物辐射的应力波产生叠加现象；全钢化真空玻璃受到的最大应力值先急速增大，而后逐渐缓慢的减小到仅受大气压强时的最大应力值。

(2) 仅针对支撑物类型这一特征进行落球冲击数值模拟分析，得到了圆环型支撑物的全钢化真空玻璃的抗冲击性能最好，球型支撑物的全钢化真空玻璃的抗冲击性能最差。

(3) 仅针对环型支撑物的排列方式这一特征进行落球冲击数值模拟分析，得到了正三角形排布的全钢化真空玻璃抗冲击性能最好，正六边形排布的全钢化真空玻璃抗冲击性能最差。

基于以上分析，选用圆环型支撑物并采用正三角形排布的全钢化真空玻璃的抗冲击性能最好。

基金项目

河南省创新示范专项资助项目(191110211600)；河南省高等学校重点科研项目计划(19A460020)。