试论弓网机械磨耗的数学模型

On the Mathematical Model of Mechanical Wear of Bow Net

摘要: 在城市轨道交通中，地铁电客车受电弓与接触线之间所产生的磨耗(简称弓网磨耗)，是常见的设备问题。而在弓网磨耗的类型中，机械磨耗占85%以上。本文以接触线的磨耗为研究对象，尝试将其机械磨耗现象纳入数学模型当中，对其进行规范化，以此建立一个规范的量化的理论系统。结合一般的量纲分析、分析力学、摩擦学理论，对弓网磨耗现象列出相关物理量，试推出量纲关系，揭示该磨耗类型的特征。通过模型的构造，可以对弓网磨耗现象的本质做出更深入的了解，对磨耗量的变化采取更有可控性的监测。

Abstract: In urban rail transit, the wear between the pantograph and the contact wire, known as the bow-net wear, is a common equipment issue. Among the types of bow-net wear, mechanical wear constitutes over 85%. This study focuses on the wear of the contact wire, aiming to integrate the mechanical wear phenomenon into a mathematical model, standardize it, and establish a standardized and quantified theoretical system. By combining dimensional analysis, analytical mechanics, and the theory of friction, relevant physical quantities related to bow-net wear are identified, dimensional relationships are derived, and the characteristics of this wear type are revealed. Through the construction of the model, a deeper understanding of the essence of bow-net wear phenomenon can be achieved, and a more controllable monitoring of wear variation can be implemented.

1. 引言

关于机械摩擦、接触磨损等理论的研究，现已取得了重要成果，尤其是摩擦学领域，被广泛应用于地铁系统弓网关系问题的处理当中。磨耗的产生有其弓网自身及外部客观等复杂原因，如外部间接磨耗、化学磨耗(环境因素)。现有的研究成果表明，直接属于弓网关系的磨耗主要分为两大类：机械磨耗与电气磨耗，其中机械磨耗是最主要也是最典型的。从常识上看，机械磨耗与接触压力有关，压力过大，抬升量会随之加大，摩擦导致的磨耗增加；而压力过小，电阻上升，接触点温度升高，二者之间产生电弧，电气磨耗增加。

传统的研究方法更多关注的是弓网关系，而忽略了磨耗现象的本身，考察范围未包含“磨耗”产生的其他各种条件，虽已定性分析，但未定量描述，仍未很好地揭示其中的复杂性。磨耗出现的一瞬间，到底发生了什么，如何去判定该现象的产生，磨耗变化的机理又是什么，从哪些侧面去反映该现象？如何去描述这一现象，它与什么因素有关？由于弓网系统是动态运作的，机械磨耗下，各种因素相互影响或作用，用数学语言去描述无疑是最直观的。

现改变以往方式，从接触线这一本体出发，从根本上对磨耗进行考察。用数学语言去描述接触线的“磨耗”现象，构建该行为的数学模型，使其直观化、计量化。运用数学语言，揭示磨耗的本质，为实际的弓网机械磨耗的相关问题解决提供理论支持。

2. 磨耗本质与量纲统一

磨耗是什么，我们平时所说的长1 m的磨耗，或者宽10 mm的磨耗，这样的表述是否合理？传统的认识，是将弓网关系不良看成是磨耗产生的根本原因，产生矛盾：几何学量纲无法对应弓网相互作用的动力学意义！从该矛盾可见：线磨耗的量L、面积磨耗的量A (L²)以及体积磨耗的量V (L³)皆为几何学量纲，对应弓网关系的动力学意义这一模式是不可行的。所以，我们必须建立“动力学过程 $\iff$ 动力学量纲”这一联系。由动力学量纲可进一步推出以下两点：

1) 磨耗的本质：接触线的变质量运动；

2) 磨耗具有动力学意义 $\Rightarrow$ 质量[m]，是磨耗真实存在的最根本的属性。几何学现象只是磨耗的一个侧面反映，非本质上的。由此，与本质相对应，磨耗的量纲统一为质量[m]，赋予该现象本质性的描述。后面所有论述皆以这两条推论为基础。

磨耗的多少或大小，表示这一种量的程度。在现实中对此说法不一，有的用接触线残余宽度来衡量，有的则用接触线的残余厚度来衡量，亦或是结合宽度与厚度一起进行评估，主要有线磨耗、面磨耗以及体积磨耗等标准。这都是有效的手段，但存在是否规范的问题。由于测量磨耗的量，本应该就磨耗掉的部分而言，但磨耗的部分无法得知其形体或其他参数，无法再还原重现磨耗部分的状态(大多呈粉末状碎屑散落)。而理论的推导需从磨耗本身着手，对磨耗的量进行数学表达。

现对磨耗进行量纲的统一，对其转化为动力学量纲，建立机械磨耗的质量m的模型。磨耗的质量m与接触线的载荷f、维氏硬度H、滑动速度v、时间t、弹性模量E、密度ρ、疲劳极限即最大应力p以及磨耗的体积V有关，今运用白金汉π定理分析质量m与上述物理量之间的关系 [1] ，由此进一步推导出其函数表达式。机械磨耗现象中所涉及的物理量及其量纲为：

磨耗质量m的SI单位是kg，基本量纲表达式为[m] = M；

总体载荷f的SI单位是N，基本量纲表达式为[f] = LMT⁻²；

维氏硬度H的SI单位是kgf/mm²，基本量纲表达式为[H] = MLMT⁻²L⁻² = M²T⁻²L⁻¹；

滑行速度v的SI单位是m/s，基本量纲表达式为[v] = LT⁻¹；

表面接触时间t的SI单位是s，基本量纲表达式为[t] = T；

弹性模量E的SI单位是N/m²，基本量纲表达式为[E] = LMT⁻²L⁻² = MT⁻²L⁻¹；

材料密度ρ的SI单位是kg/m³，基本量纲表达式为[ρ] = ML⁻³；

最大应力P的SI单位是Pa，基本量纲表达式为[P] = LMT⁻²L⁻² = MT⁻²L⁻¹与弹性模量的量纲一致，故合并为同一动力学量纲的量。

磨耗体积V的SI单位是m³，基本量纲表达式为[V] = L³；

质量m与相关量的函数表达式可写成 $m=m\left(f,H,v,t,E,\rho ,V\right)$ ，则有原函数关系式为 $\phi \left(m,f,H,v,t,E,\rho ,V\right)=0$ 。可知上述物理量所涉及的基本量纲为L、M、T，得出量纲矩阵 $A^{\text{T}}=\left[\begin{array}{cccccccc}0& 1& -1& 1& 0& -1& -3& 3\\ 1& 1& 2& 0& 0& 1& 1& 0\\ 0& -2& -2& -1& 1& -2& 0& 0\end{array}\right]\begin{array}{c}\text{L}\\ \text{M}\\ \text{T}\end{array}$ ，可得 $\text{rank}\left(A\right)=\text{3}$ 。在8个物理量中选出3个量纲相互独立的变量ρ、v、f，则无量纲积有 $\text{8}-\text{rank}\left(A\right)=\text{5}$ 组，这5组积作为无量纲量的函数关系式为 $\psi \left({\pi }_1,{\pi }_2,{\pi }_3,{\pi }_4,{\pi }_5\right)=0$ ，无量纲积的组合分别用基本物理量的幂次乘积形式表示为： ${\pi }_1=m{\rho }^{{\alpha }_1}{v}^{{\beta }_1}{f}^{{\gamma }_1}$ ， ${\pi }_2=H{\rho }^{{\alpha }_2}{v}^{{\beta }_2}{f}^{{\gamma }_2}$ ， ${\pi }_3=t{\rho }^{{\alpha }_3}{v}^{{\beta }_3}{f}^{{\gamma }_3}$ ， ${\pi }_4=E{\rho }^{{\alpha }_4}{v}^{{\beta }_4}{f}^{{\gamma }_4}$ ， ${\pi }_5=V{\rho }^{{\alpha }_5}{v}^{{\beta }_5}{f}^{{\gamma }_5}$ ，转换成量纲形式为：

$\left[{\pi }_1\right]=M{\left(M{L}^{-3}\right)}^{{\alpha }_1}{\left(L{T}^{-1}\right)}^{{\beta }_1}{\left(LM{T}^{-2}\right)}^{{\gamma }_1}=L^0{M}^0{T}^0$ (1)

$\left[{\pi }_2\right]=M^2{T}^{-2}{L}^{-1}{\left(M{L}^{-3}\right)}^{{\alpha }_2}{\left(L{T}^{-1}\right)}^{{\beta }_2}{\left(LM{T}^{-2}\right)}^{{\gamma }_2}=L^0{M}^0{T}^0$ (2)

$\left[{\pi }_3\right]=T{\left(M{L}^{-3}\right)}^{{\alpha }_3}{\left(L{T}^{-1}\right)}^{{\beta }_3}{\left(LM{T}^{-2}\right)}^{{\gamma }_3}=L^0{M}^0{T}^0$ (3)

$\left[{\pi }_4\right]=M{T}^{-2}{L}^{-1}{\left(M{L}^{-3}\right)}^{{\alpha }_4}{\left(L{T}^{-1}\right)}^{{\beta }_4}{(LM{T}^{-2})}^{{\gamma }_4}=L^0{M}^0{T}^0$ (4)

$\left[{\pi }_5\right]=L^3{\left(M{L}^{-3}\right)}^{{\alpha }_5}{\left(L{T}^{-1}\right)}^{{\beta }_5}{\left(LM{T}^{-2}\right)}^{{\gamma }_5}=L^0{M}^0{T}^0$ (5)

由式(1)得方程组 $\{\begin{array}{l}-3{\alpha }_1+{\beta }_1+{\gamma }_1=0\\ 1+{\alpha }_1+{\gamma }_1=0\\ -{\beta }_1-2{\gamma }_1=0\end{array}$ ，求解得 ${\alpha }_1=\frac{1}{2}$ ， ${\beta }_1=3$ ， ${\gamma }_1=-\frac{3}{2}$ ，所以 ${\pi }_1=m{\rho }^{\frac{1}{2}}{v}^3{f}^{-\frac{3}{2}}$ ；

由式(2)得方程组 $\{\begin{array}{l}-1-3{\alpha }_2+{\beta }_2+{\gamma }_2=0\\ 2+{\alpha }_2+{\gamma }_2=0\\ -2-{\beta }_2-2{\gamma }_2=0\end{array}$ ，求解得 ${\alpha }_2=-\frac{1}{2}$ ， ${\beta }_2=1$ ， ${\gamma }_2=-\frac{3}{2}$ ，所以 ${\pi }_2=H{\rho }^{-\frac{1}{2}}v{f}^{-\frac{3}{2}}$ ；

由式(3)得方程组 $\{\begin{array}{l}-3{\alpha }_3+{\beta }_3+{\gamma }_3=0\\ {\alpha }_3+{\gamma }_3=0\\ 1-{\beta }_3-2{\gamma }_3=0\end{array}$ ，求解得 ${\alpha }_3=\frac{1}{2}$ ， ${\beta }_3=2$ ， ${\gamma }_3=-\frac{1}{2}$ ，所以 ${\pi }_3=t{\rho }^{\frac{1}{2}}{v}^2{f}^{-\frac{1}{2}}$ ；

由式(4)得方程组 $\{\begin{array}{l}-1-3{\alpha }_4+{\beta }_4+{\gamma }_4=0\\ 1+{\alpha }_4+{\gamma }_4=0\\ -2-{\beta }_4-2{\gamma }_4=0\end{array}$ ，求解得 ${\alpha }_4=-1$ ， ${\beta }_4=-2$ ， ${\gamma }_4=0$ ，所以 ${\pi }_4=E{\rho }^{-1}{v}^{-2}$ ；

由式(5)得方程组 $\{\begin{array}{l}3-3{\alpha }_5+{\beta }_5+{\gamma }_5=0\\ {\alpha }_5+{\gamma }_5=0\\ -{\beta }_5-2{\gamma }_5=0\end{array}$ ，求解得 ${\alpha }_5=\frac{3}{2}$ ， ${\beta }_5=3$ ， ${\gamma }_5=-\frac{3}{2}$ ，所以 ${\pi }_5=V{\rho }^{\frac{3}{2}}{v}^3{f}^{-\frac{3}{2}}$ ；

其中由 ${\pi }_1$ 可得 $m=\pi {\rho }^{-\frac{1}{2}}{v}^{-3}{f}^{\frac{3}{2}}$ ，又因无量纲量的方程 $\psi \left({\pi }_1,{\pi }_2,{\pi }_3,{\pi }_4,{\pi }_5\right)=0$ 与 $\phi \left(m,f,H,v,t,E,\rho ,V\right)=0$ 等价，即磨耗质量m的显式表达式为： $m={\rho }^{-\frac{1}{2}}{v}^{-3}{f}^{\frac{3}{2}}\Psi \left({\pi }_2,{\pi }_3,{\pi }_4,{\pi }_5\right)={\rho }^{-\frac{1}{2}}{v}^{-3}{f}^{\frac{3}{2}}\Psi \left(H{\rho }^{-\frac{1}{2}}v{f}^{-\frac{3}{2}},t{\rho }^{\frac{1}{2}}{v}^2{f}^{-\frac{1}{2}},E{\rho }^{-1}{v}^{-2},V{\rho }^{\frac{3}{2}}{v}^3{f}^{-\frac{3}{2}}\right)=0$ ，虽然Ψ为待求函数，但整体在应用中已大大趋近于原型，对于物理模拟的意义重大。磨耗的量纲统一以质量的量纲M定义，“磨耗”即是指磨耗的质量。统一了量的动力学量纲，这是解决相关问题的第一步，任何数据分析应以此为基础。m是数学模型中的量，通过量纲分析得出其函数表达式，而它与实际的磨耗质量 $\tilde{m}$ 到底有多接近，取决于实际试验中有多少条件是可以满足模型条件的。假设实际测量时，我们找到H、v、t、E、ρ、V等容易满足的条件，那么 ${\pi }_2$ 、 ${\pi }_3$ 、 ${\pi }_4$ 、 ${\pi }_5$ 等无量纲量就是等效的，原型的质量与模型的质量仅存在关系 $\tilde{m}/m={\left(\tilde{f}/f\right)}^{\frac{3}{2}}$ ，式中 $\tilde{f}$ 为原型的载荷，则测量原型的磨耗质量 $\tilde{m}$ 已得到较大简化。

3. 关于磨耗的标准计算公式的推导

接触线是一个均匀密度的刚体，即任意同单位的两处质量都是相同的，所以被磨耗掉的部分同样满足均质条件。见图1，将接触线磨损掉的部分重新组合还原，可得到一个立方体，即磨耗体。磨耗体基本上呈现不规则的形体，而“不规则”是指该立方体上半部分而言，下半部分是原接触线的柱面部分，故有其相关的规则性。横向观察，形如图1所示，现计算其质量m。又因密度是已知的，故其体积大小起决定作用。由于接触线磨耗掉的部分，是个不规则的立方体，需分切成不同截面积大小的平面。

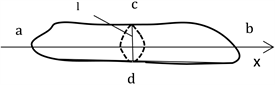
Figure 1. Schematic diagram of contact wire wearing body restoration

图1. 接触线磨耗体还原简图

若以 $A_i$ 表示不同平面的面积，且同一面积大小的平面到另一面积大小的平面的距离(厚度)为 $h_i$ ，则可求出相应的体积元： $V_1=A_1\cdot h_1$ ， $V_2=A_2\cdot h_2$ ， $\cdots$ ， $V_i=A_i\cdot h_i$ 。整体体积则为对各体积元进行求和：

$V=V_1+V_2+\cdots +V_i={\displaystyle \sum V_i}={\displaystyle \sum \left(A_i\cdot h_i\right)}$ , ( $i=1,2,\cdots ,n$ ) (6)

现将磨耗的立方体放置于一条直线坐标轴X轴上，且令每个截面皆垂直于X轴，立方体的两端所处在X轴上的位置分别记作a、b，则面积 $A_i$ 为x的标量连续函数，记作 $A_i\left(x\right)$ ，是表示经过点x且垂直于X轴的平面面积。每个相同平面的厚度 $h_i$ 则为 $x_i+\Delta x$ 或 $x_i+\text{d}x$ ，那么每个相同平面的体积元为 $\Delta V_i=A_i\left(x\right)\Delta x$ 或 $\text{d}{V}_i=A_i\left(x\right)\text{d}x$ ，两边积分得到体积关于截面面积的公式： $V={\displaystyle {\int }_a^{b}A\left(x\right)\text{d}x}$ ，由于 $A\left(x\right)$ 又是关于截面上曲边的积分，假设垂直于X轴且与截面 $A_i$ 相交的直线为l，交点记为c、d，沿l切分成的两条曲线分别记作 $\phi \left(l\right)$ 、 $\Psi \left(l\right)$ ，体积的积分为二重积分公式： $V={\displaystyle {\int }_a^b\left[{\displaystyle {\int }_c^d\phi \left(l\right)\text{d}l}+{\displaystyle {\int }_c^d\Psi \left(l\right)\text{d}l}\right]\text{d}x}$ ，故式(6)可表示为：

$V=V_1+V_2+\cdots +V_i={\displaystyle {\sum }_{i=0}^n{V}_i}={\displaystyle {\sum }_{i=0}^n\left(A_i\cdot h_i\right)}={\displaystyle {\int }_a^{b}A\left(x\right)\text{d}x}={\displaystyle {\int }_a^b\left[{\displaystyle {\int }_c^d\phi \left(l\right)\text{d}l}+{\displaystyle {\int }_c^d\Psi \left(l\right)\text{d}l}\right]\text{d}x}$

磨耗量 $m=\rho V$ ，当磨耗量为0，即无磨耗时， $V=0$ ， $A\left(x\right)=0$ ，磨耗的大小随体积的变化而变化。为进行可量化的数学计算，一般以理想情况下即截面上曲边为直线的磨耗体积为近似计算的标准，如图1所示。

Figure 2. Cross section of contact wire

图2. 接触线横截面

见图2，已知接触线的截面为左右上方有缺口的类圆形状，半径为R，定类圆心O为原点，铅垂向下引出一条直线坐标轴X轴，磨耗的截面为阴影部分。不论是否为侧磨，磨耗截面的上边线为直线L，下边线为圆弧的一部分。薄片dx即为磨耗高度的位置距离原点O的距离x的微分，直线 $L=2\sqrt{R^2-x^2}$ ，薄片的面积即为： $A_{\text{d}x}=2\sqrt{R^2-x^2}\text{d}x$ ，又下边线与X轴的交点与原点O的距离仍是R，磨耗的截面则有公式： $A\left(x\right)={\displaystyle {\int }_x^{R}2\sqrt{R^2-x^2}\text{d}x}=2{\displaystyle {\int }_x^R\sqrt{R^2-x^2}\text{d}x}$ ，对积分式子进行展开，得：

$\begin{array}{c}A\left(x\right)=2{\displaystyle {\int }_x^R\sqrt{R^2-x^2}\text{d}x}\\ =2\left(\frac{R}{2}\sqrt{R^2-R^2}+\frac{R^2}{2}\arcsin \frac{R}{R}-\frac{x}{2}\sqrt{R^2-x^2}-\frac{R^2}{2}\arcsin \frac{x}{R}\right)\\ =\pi R^2-x\sqrt{R^2-x^2}-R^2\arcsin \frac{x}{R}\end{array}$ (7)

由于式中x属于接触线的残余厚度，并不在磨耗体当中，故令磨耗的截面高度 $h=R-x$ 替换残余厚度x，式(7)可写成： $\begin{array}{c}A\left(R-h\right)=\pi R^2-\left(R-h\right)\sqrt{R^2-{\left(R-h\right)}^2}-R^2\arcsin \frac{R-h}{R}\\ =\pi R^2-\left(R-h\right)\sqrt{2Rh-h^2}-R^2\arcsin \frac{R-h}{R},\end{array}$ 所以 $V=\left(b-a\right)\cdot A\left(R-h\right)$ ，磨耗量m的标准计算公式为：

$\begin{array}{c}m=\rho V=\rho \left(b-a\right)\cdot A\left(R-h\right)\\ =\rho \left(b-a\right)\pi R^2-\rho \left(b-a\right)\left(R-h\right)\sqrt{2Rh-h^2}-\rho \left(b-a\right)R^2\arcsin \frac{R-h}{R}\end{array}$

式中：ρ——接触线密度；

$\left(b-a\right)$ ——磨耗体的长度，a、b分别为磨耗体在坐标轴上的端点 $\left(b>a\right)$ ；

R——磨耗体圆弧部分的曲率半径，或接触线圆弧半径；

h——磨耗体截面的高度。当接触线无磨耗时，h = 0。

4. 关于机械磨耗的动力学模型

在城市地铁线路中，接触网(轨)系统常见的架设方式有刚性、柔性以及第三轨，其中涉及到弓网磨耗的则是刚性、柔性接触网。刚、柔性接触网二者虽在架设类型上有别，但接触线的悬挂方式最直接的差别也仅体现在设备弹性上。

刚性接触网中的接触线是通过汇流排定位线夹与其他设备连接(以CTA120型的接触线、B型的刚性汇流排定位线夹为例)，由于CTA120型接触线的(沟)槽尖间距为6.8 mm，而刚性汇流排最底部的夹持宽度为4.8 mm，故接触线与汇流排之间无相对运动，可视为同一刚体系。而汇流排与定位线夹之间则存在可活动的裕度，因B型汇流排定位线夹的开档间距为89.4 mm，对于汇流排顶部的宽度85 mm而言具有垂直线路方向的4.4 mm活动裕度；又B型汇流排定位线夹开档的上下间隙为9 mm，较之汇流排顶部的厚度6 mm而言具有竖直方向的3 mm活动裕度。柔性接触网对比刚性接触网，其接触线则具有更大的弹性空间，以及活动裕度。

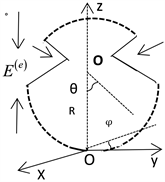
Figure 3. Schematic diagram of contact wire

图3. 接触线自由度示意

由此可见，电客车受电弓碳滑板运动过程中，接触线并非处于静止无运动状态，而是由相应的活动裕度提供了随悬挂装置进行进动、章动的条件。接触线的运动自由度实现了延拓。取弓网系统中接触线及受电弓碳滑板(即摩擦副)作为考察整体，弓网运作时，接触线与碳滑板做相对运动。将碳滑板作为参考系，则接触线贴碳滑板表面沿碳滑板的前进方向做逆方向运动。接触线所处在的动力学系统，是一个存在耗散的、非理想的、非保守的系统，主动力摩擦阻力作功，机械能不守恒 [2] 。见图3，那么接触线所受的外力有悬挂部件的夹持力与悬吊力 $F_1^{\left(e\right)}$ ，以及受电弓碳滑板的支持力 $F_2^{\left(e\right)}$ 。其中 $F_2^{\left(e\right)}$ 由受电弓抬升量及弓网接触力体现，当其足够小时趋近于0，由于振动与其有关，故在动力学分析中不忽略。又因为接触线的架设以“之”字值进行，所以接触线沿碳滑板斜向运动，刚性汇流排(或柔性悬挂接触线)在垂直线路方向的活动裕度使得接触线存在欧拉角的进动角φ，而刚性汇流排(或柔性悬挂接触线)在竖直方向的活动裕度又使得接触线存在欧拉角的章动角θ。以接触线运动为主体，根据约束条件可得出广义坐标 $q_k$ 有：x、θ、φ。在t时刻弓网接触点处的振幅为A，由于两边凹槽收到夹持力的作用，θ角产生的应力只转化为上下振动的激励，而不产生以Y轴为主轴的转动。无论振动的微小与否，振动的动能 $E_k=\frac{1}{2}k{A}^2{\text{e}}^{-\beta t}\sin \Omega t$ ( $\beta$ 为阻尼系数)寓于作用于Z轴上的动能。耗散系统的拉格朗日方程为：

$\frac{\text{d}}{\text{d}t}\left(\frac{\partial L}{\partial {\stackrel{\dot{}}{q}}_k}\right)-\frac{\partial L}{\partial q_k}=Q_k+Q_D$ (8)

则位移有： $\text{d}r=\left(\text{d}x+x\text{d}\phi \right)e_x+R\left(\text{d}\phi +\text{d}\theta \right)e_y+R\text{d}\theta e_z$ ，对时间求导，得速度： $\stackrel{\dot{}}{r}=\left(\stackrel{\dot{}}{x}+x\stackrel{\dot{}}{\phi }\right)e_x+R\left(\stackrel{\dot{}}{\phi }+\stackrel{\dot{}}{\theta }\right)e_y+R\stackrel{\dot{}}{\theta }{e}_z$ ，根据欧拉角方程，章动角θ与进动角φ满足： ${\omega }_x=\stackrel{\dot{}}{\theta }$ ， ${\omega }_y=\stackrel{\dot{}}{\phi }\sin \theta$ ， ${\omega }_z=\stackrel{\dot{}}{\phi }\cos \theta$ ，故动能为：

$\begin{array}{c}T=\frac{1}{2}m{\stackrel{\dot{}}{r}}^2+\frac{1}{2}I{\omega }^2\\ =\frac{1}{2}m\left({\stackrel{\dot{}}{x}}^2+x^2{\stackrel{\dot{}}{\phi }}^2+{\stackrel{\dot{}}{\phi }}^2{R}^2+{\stackrel{\dot{}}{\theta }}^2{R}^2+{\stackrel{\dot{}}{\theta }}^2{R}^2\right)+\frac{1}{2}I\left({\stackrel{\dot{}}{\theta }}^2+{\stackrel{\dot{}}{\phi }}^2{\sin }^2\theta +{\stackrel{\dot{}}{\phi }}^2{\cos }^2\theta \right)\\ =\frac{1}{2}m{\stackrel{\dot{}}{x}}^2+\frac{1}{2}m{x}^2{\stackrel{\dot{}}{\phi }}^2+\frac{1}{2}m{\stackrel{\dot{}}{\phi }}^2{R}^2+m{\stackrel{\dot{}}{\theta }}^2{R}^2+\frac{1}{2}I\left({\stackrel{\dot{}}{\theta }}^2+{\stackrel{\dot{}}{\phi }}^2\right)\end{array}$ (9)

势能 $V=mg\left(R-R\cos \theta \right)+\frac{1}{2}{k}^2{\left(R-R\cos \theta \right)}^2{\text{e}}^{-2\beta t}\cos \Omega t$ (10)

则式(9)~(10)得出拉格朗日函数：

$\begin{array}{c}L=T-V\\ =\frac{1}{2}m{\stackrel{\dot{}}{x}}^2+\frac{1}{2}m{x}^2{\stackrel{\dot{}}{\phi }}^2+\frac{1}{2}m{\stackrel{\dot{}}{\phi }}^2{R}^2+m{\stackrel{\dot{}}{\theta }}^2{R}^2+\frac{1}{2}I\left({\stackrel{\dot{}}{\theta }}^2+{\stackrel{\dot{}}{\phi }}^2\right)\\ -mg\left(R-R\cos \theta \right)-\frac{1}{2}{k}^2{\left(R-R\cos \theta \right)}^2{\text{e}}^{-2\beta t}\cos \Omega t\end{array}$ (11)

耗散函数 $D={\mu }_i{v}_i=\mu \left(\stackrel{\dot{}}{x}+x\stackrel{\dot{}}{\phi }\right)+\mu R\left(\stackrel{\dot{}}{\phi }+\stackrel{\dot{}}{\theta }\right)+\mu R\stackrel{\dot{}}{\theta }$ ，又因保守力的广义力 $Q_k={{\displaystyle \sum }}^{\text{}}\left(Q_{kx},Q_{k\theta },Q_{k\phi }\right)$ ；耗散力的广义力 $Q_D={{\displaystyle \sum }}^{\text{}}\left(Q_{Dx},Q_{D\theta },Q_{D\phi }\right)$ ，可求出广义坐标 $q_k$ 所对应的广义力，并由式(11)与式(8)计算、化简得到以下结果。

x方向上的运动方程： $\frac{\text{d}}{\text{d}t}\left(m\stackrel{\dot{}}{x}\right)-mx{\stackrel{\dot{}}{\phi }}^2=-\mu$ ，故 $m\ddot{x}-mx{\stackrel{\dot{}}{\phi }}^2+\mu =0$ ；

$\theta$ 方向上的运动方程： $\begin{array}{l}\frac{\text{d}}{\text{d}t}\left(2m\stackrel{\dot{}}{\theta }{R}^2+I\stackrel{\dot{}}{\theta }\right)-mgR\sin \theta -\left(k^2{R}^2{\cos }^2\theta \sin \theta -k^2{R}^2\sin \theta \right){\text{e}}^{-2\beta t}\cos \Omega t\\ =-2\mu R-mgR\sin \theta -\left(k^2{R}^2{\cos }^2\theta \sin \theta －k^2{R}^2\sin \theta \right){\text{e}}^{-2\beta t}\cos \Omega t,\end{array}$ 两边化简得 $2m{R}^2\ddot{\theta }+I\ddot{\theta }+2\mu R=0$ ；

$\phi$ 方向上的运动方程： $\frac{\text{d}}{\text{d}t}\left(m{x}^2\stackrel{\dot{}}{\phi }+m{R}^2\stackrel{\dot{}}{\phi }+I\stackrel{\dot{}}{\phi }\right)=-\mu x-\mu R$ ，故 $2mx\stackrel{\dot{}}{x}\ddot{\phi }+m{R}^2\ddot{\phi }+I\ddot{\phi }+\mu x+\mu R=0$ ，至此，所求出的接触线的运动微分方程皆为广义坐标的二阶微分方程： $\{\begin{array}{l}m\ddot{x}-mx{\stackrel{\dot{}}{\phi }}^2+\mu =0\\ 2m{R}^2\ddot{\theta }+I\ddot{\theta }+2\mu R=0\\ 2mx\stackrel{\dot{}}{x}\ddot{\phi }+m{R}^2\ddot{\phi }+I\ddot{\phi }+\mu x+\mu R=0\end{array}$ ，其中 $\mu$ 为摩擦系数，对方程组进行变形，得到 $\mu$ 的表达式： $\{\begin{array}{l}\mu =m\ddot{x}-mx{\stackrel{\dot{}}{\phi }}^2\\ \mu =-\frac{2m{R}^2\ddot{\theta }+I\ddot{\theta }}{2R}=0\\ \mu =-\frac{2mx\stackrel{\dot{}}{x}\ddot{\phi }+m{R}^2\ddot{\phi }+I\ddot{\phi }}{x+R}=0\end{array}$ ，由于转动惯量I与质量m有关，故写成 $I=m\cdot \square$ 的形式，其中方框□是一个待求因式，且□与m无关，故方程组中的 $\mu$ 可表示为： $\mu =-m\ddot{x}\left(1-\frac{x{\stackrel{\dot{}}{\phi }}^2}{\ddot{x}}\right)$ ， $\mu =-m\ddot{\theta }\left(R+\frac{\square }{2R}\right)$ ， $\mu =-m\ddot{\phi }\left(\frac{2x\stackrel{\dot{}}{x}+R^2+\square }{x+R}\right)$ ，可见 $\mu$ 在形式上与前

进方向上的加速度 $\ddot{x}$ 反向，与章动角的加速度 $\ddot{\theta }$ 反向，与进动角的加速度 $\ddot{\phi }$ 反向。由于接触线的自由度以x为主，运动状态以x方向上的贡献最为突出，故考察x方向上方程的意义最重要。令：

$\mu =-m\ddot{x}\left(1-\frac{x{\stackrel{\dot{}}{\phi }}^2}{\ddot{x}}\right)=-m\ddot{x}\cdot ○$ ，其中 $○=1-\frac{x{\stackrel{\dot{}}{\phi }}^2}{\ddot{x}}$ (12)

式中○同样是一个待求因式。实际上 $\mu$ 是一个标量，无方向， $\mu$ 与摩擦作用力 $F_N$ 成反比，由于 $\ddot{\theta }$ 、 $\ddot{\phi }$ 与转动惯量I方向相反，而 $\ddot{x}$ 与x同向，故有 $1-\frac{x{\stackrel{\dot{}}{\phi }}^2}{\ddot{x}}<0$ ，即因式 $○<0$ 。

无论磨耗量的大小，产生磨耗的接触线皆是一个变质量体，整体质量随时间发生减少的变化，即 $\frac{\text{d}m}{\text{d}t}<0$ ，dm即接触线损失的质量，也就是磨耗量。从磨耗的角度上看， $\frac{\text{d}m}{\text{d}t}$ 的范围是随机的，即磨耗率并不确定为某一常数(下文将讨论)。由密舍尔斯基方程得出： $m\ddot{r}=F+\stackrel{\dot{}}{m}\left(\stackrel{\dot{}}{r}-u\right)$ ，式中 $F$ 为dt时间内的合外力， $u$ 为磨耗体dm脱离接触线的速度。令 $\stackrel{\dot{}}{r}=u$ ，即dm的速度与接触线的速度一致，磨耗与接触线未分离或磨耗未产生，则 $m\ddot{r}=F$ ，即接触线的质量未随时间而改变。又因耗散力 $F=-\frac{\mu u}{\left|u\right|}$ 时表现为摩擦力 $F_N$ ，即 $F_N=-\mu e_r$ ，摩擦系数乘以一个方向的单位向量。故 $\mu =-\left|F_N\right|$ ，又由式(12)中 $\mu =-m\ddot{x}\cdot ○$ 这一形式可见， $-\left|F_N\right|=-m\ddot{x}\cdot ○$ ，所以 $F=m\ddot{r}$ 即为摩擦力 $F_N$ ！现将密舍尔斯基方程进行整理，得到公式： $-F_N=-m\ddot{r}+\stackrel{\dot{}}{m}\left(\stackrel{\dot{}}{r}-u\right)$ ，故 $-m\ddot{x}\cdot ○=-m\ddot{r}+\stackrel{\dot{}}{m}\left(\stackrel{\dot{}}{r}-u\right)$ ， $○=\frac{\ddot{r}}{\ddot{x}}-\frac{\stackrel{\dot{}}{m}\stackrel{\dot{}}{r}-\stackrel{\dot{}}{m}u}{m\ddot{x}}$ ，一般情况下， $\ddot{x}=\ddot{r}\cdot \cos \left(\ddot{x},\ddot{r}\right)$ ，当方向夹角 $\left(\ddot{x},\ddot{r}\right)$ 趋于0时，有 ${\lim }_{\left(\ddot{x},\ddot{r}\right)\to 0}\cos \left(\ddot{x},\ddot{r}\right)=1$ ，或进行泰勒展开亦同。所以当方向夹角 $\left(\ddot{x},\ddot{r}\right)$ 足够小时，可认为 $\ddot{x}=\ddot{r}$ 。现实中 $\left(\ddot{x},\ddot{r}\right)$ 甚至会很微小，并不会太大，则 $○=1-\frac{\stackrel{\dot{}}{m}\stackrel{\dot{}}{r}-\stackrel{\dot{}}{m}u}{m\ddot{x}}$ ，由式(12)进替换， $1-\frac{x{\stackrel{\dot{}}{\phi }}^2}{\ddot{x}}=1-\frac{\stackrel{\dot{}}{m}\stackrel{\dot{}}{r}-\stackrel{\dot{}}{m}u}{m\ddot{x}}$ ，化简得出：

$mx{\stackrel{\dot{}}{\phi }}^2=\stackrel{\dot{}}{m}\stackrel{\dot{}}{r}-\stackrel{\dot{}}{m}u$ (13)

讨论式(13)中，当 $u=0$ 时， $mx{\stackrel{\dot{}}{\phi }}^2=\stackrel{\dot{}}{m}\stackrel{\dot{}}{r}$ ，而在前进方向上位移 $x\approx t\stackrel{\dot{}}{r}$ ，故 $m\cdot t\stackrel{\dot{}}{r}{\stackrel{\dot{}}{\phi }}^2=\stackrel{\dot{}}{m}\stackrel{\dot{}}{r}$ ，化简得 $m{\stackrel{\dot{}}{\phi }}^{2}t=\stackrel{\dot{}}{m}$ ，由 $I=m\cdot \square$ 对式子进一步整理，得出 $\frac{1}{2}I{\stackrel{\dot{}}{\phi }}^{2}t=\stackrel{\dot{}}{m}\cdot \frac{1}{2}\cdot \square$ ，由于转动惯量I与接触线初始质量m都是确定的，故 $\frac{1}{2}\cdot \square =\text{const}$ ，令常数 $c=\frac{1}{2}\cdot \square$ ，推导出关系式：

$T_{\phi }t=\stackrel{\dot{}}{m}\cdot c$ (14)

可见，磨耗量dm随时间的变化率 $\frac{\text{d}m}{\text{d}t}$ 与进动角 $\phi$ 所产生的动能 $T_{\phi }$ 有关。当磨耗产生时， $u\ne \stackrel{\dot{}}{r}$ ，磨耗体脱离接触线，存在 $u_{\min }=0$ 时，即磨耗体在水平方向的速度为0时，磨耗体呈现垂直或竖直方向脱落，摆动角度的动能等于接触线质量随时间的变化率与接触线初始质量的比值乘以一个常数c。相反可推出，当进动角 $\phi$ 的动能 $T_{\phi }$ 在一个单位时间中达到 $\stackrel{\dot{}}{m}\cdot c$ 这一个值时，磨耗现象出现。可将出现磨耗的临界值写为： $T_{{\phi }_{\min }}=\stackrel{\dot{}}{m}\cdot c$ 。在式(13)中，当 $u=\stackrel{\dot{}}{r}$ 时， $mt{\stackrel{\dot{}}{\phi }}^2=0$ ，即 $\stackrel{\dot{}}{\phi }=0$ ，表示当接触线未发生进动时，接触线整体只以一个速度 $\stackrel{\dot{}}{r}$ 运动，未出现速度不一致的分体运动，故未出现磨耗现象。其中 $\stackrel{\dot{}}{m}$ 的量纲式为MT⁻¹，故由 $T_{\phi }$ 的量纲式ML²T⁻²进一步检验出常数c的量纲式为L²T⁻¹，其物理意义如同位移与速度相乘。

综上所述，本文所构建的动力学模型是以接触线活动裕度为基础的，抽象出广义坐标，能够将机械磨耗的产生原理直观化、清晰化，使磨耗现象的研究进一步本质化。将接触线所受外力等价平移至悬挂部件所受的力，目的在于接触线的运动状态得以完备化。以弹性性能最小的架空刚性接触网为例，接触线在垂直线路方向上具有的4.4 mm活动裕度，故接触线活动裕度的范围在垂直线路方向上≥4.4 mm时， $T_{{\phi }_{\min }}=\stackrel{\dot{}}{m}\cdot c$ (将 $T_{\phi }t=\stackrel{\dot{}}{m}\cdot c$ 中的时间t单位化后)这一动力学效应对于机械磨耗的产生是有意义的。在4.4 mm量级上，总加速度 $\ddot{r}$ 与分量加速度 $\ddot{x}$ 十分接近，方向夹角 $\left(\ddot{x},\ddot{r}\right)$ 存在趋于0的可能。正因如此， $\stackrel{\dot{}}{\phi }$ 即使不等于0，也是属于一个小量，表明 $T_{{\phi }_{\min }}$ 可以足够小，亦能促使磨耗的产生，只是磨耗量的大小可能需要以微观层面的手段进行测量而已。此时，宏观上的摩擦所产生的质量损耗已内蕴于进动角的动能之中！

在动力学模型的基础上，再论其稳定性，对接触线本体而言，接触线的运动状态是稳定的。在架设的线路设计当中，实际的接触线运动是符合要求未发生偏离的。在三个自由度中，顺线路方向的x是按照设计来架设的，具有硬性要求，而 $\theta$ 、 $\phi$ 则是在一定范围内允许存在的，具有弱约束性，在mm量级上合理的自由度。在数学物理意义中， $\theta$ 、 $\phi$ 等同于对接触线在x方向上运动所施加的微扰，两个微扰产生于定位点处。经过有限的时间，接触线的振动减小最后恢复原状态。在位形空间中，相轨迹由相点所体现，而现实中虽然接触线以x方向位移最显著，做功最多，但其在磨耗产生上并不起直接、明显的作用，接触线出现磨耗现象的一瞬间，是因为进动角 $\phi$ 的动能 $T_{\phi }$ 对此产生了贡献。而章动角 $\theta$ 所引起的微扰作用，使得磨耗的位置出现偏斜，即侧磨。

5. 关于机械磨耗的随机模型

磨耗现象的过程，是无法在线检测的。这是由于引发磨耗产生的各种条件复杂，使之具有无法预知性，从而其随机性强。大多数情况下，只能将磨耗前后的数据进行对比分析。

根据现有的摩擦学理论，磨耗行为分为三个阶段：自组织阶段，即磨合磨损期；混沌阶段，即正常磨耗期；失稳阶段，即急剧磨耗期 [3] 。从接触线与受电弓碳滑板接触表面的形貌来看，理想情况下磨耗进行到接触线表面最底层(无微凸体)时，表面达到理想光滑，不再出现磨耗，然而实际上磨耗会持续进行。首先可知，当弓网接触压力超过屈服极限时，会发生微观切削和塑性变形，其中一些磨屑存在于摩擦界面，参与磨耗行为；另有一部分挤入凹谷，使表面逐渐平滑。在磨耗过程中，微凸体在界面发生粘着(熔焊)，出现撕裂。

见图4，接触线表面的高度记为 $z_i$ ，表面的高度服从正态分布 [4] ，即 ${\phi }_0\left(z\right)=\frac{1}{\sqrt{2\pi }\sigma }{\text{e}}^{-\frac{{\left(z-\mu \right)}^2}{2{\sigma }^2}}$ ，式中 ${\sigma }^2$ 为高度的方差， $\mu$ 为高度平均值。在 $\left(-3{\sigma }^2,3{\sigma }^2\right)$ 区间内，密度最大，微凸体高度最为集中，也就是磨耗发生的概率相对较大。

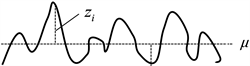
Figure 4. Surface morphology of contact wire

图4. 接触线表面形态

通过观察分析，可认定表面的高度分布具有以下重要特征：无记忆性，即与时间无关。平均高度值随时间发生表动，但高度分布仍然是具有正态性的。如同一个青少年群体内的成员，最初的统计身高符合正态分布，随着年龄的增长，即使每位成员的身高发生变化，但最后的统计结果仍然是正态分布的。此特征表明，接触线的表面在磨耗前后，表面高度都是服从正态分布的。则设磨耗后的高度为 $Z^{\prime }$ ，存在 $Z^{\prime }=Z-kt$ (k为高度的磨耗率，t为时间，kt为磨耗量)。分布函数 $\psi \left(z^{\prime }\right)=P\left\{Z^{\prime }\le z^{\prime }\right\}=P\left\{Z-kt\le z^{\prime }\right\}=P\left\{Z\le z^{\prime }+kt\right\}={\psi }_0\left(z^{\prime }+kt\right)$ ， ${\psi }_0$ 为初始的表面高度分布函数，所以磨耗后的密度函数有：

$\phi \left(z^{\prime }\right)=\frac{1}{\sqrt{2\pi }{\sigma }^{\prime }}{\text{e}}^{-\frac{{\left(z^{\prime }-\left(\mu -kt\right)\right)}^2}{2{{\sigma }^{\prime }}^2}}$ (15)

磨耗前后的表面高度都服从正态分布，那么考察式子 $Z^{\prime }=Z-kt$ 成为关键。Z与 $Z^{\prime }$ 的正态分布已确定，则Z与 $Z^{\prime }$ 呈线性关系，kt分为两种情况：第一种是常数，从实际与理论上观察这是不可能的，表现在表面高度上的磨耗率k是随机的，并非恒定常数；另一种是服从正态分布的随机变量，并且可确定的是kt是独立于Z与 $Z^{\prime }$ 的随机变量。排除第一种可能性后，kt的定位则确定为正态随机变量。式(15)中具有两个随机变量： $z^{\prime }$ 与kt，将 $z^{\prime }$ 用一般的z表示，即表面高度与变化量同时以正态分布的密度函数呈现，式(15)写成二维密度函数：

$\phi \left(z,kt\right)=\frac{1}{\sqrt{2\pi }\sigma }{\text{e}}^{-\frac{{\left(z-\left(\mu -kt\right)\right)}^2}{2{\sigma }^2}}$ (16)

式(16)比上 ${\phi }_0\left(z\right)$ 则可得出磨耗量kt在Z条件下的条件密度函数： ${\phi }_{kt|z}\left(kt|z\right)=\frac{\phi \left(z,kt\right)}{{\phi }_0\left(z\right)}={\text{e}}^{\frac{\mu \left(1-z\right)}{{\sigma }^2}}\cdot {\text{e}}^{\frac{kt\left(2\mu -kt-2\right)}{2{\sigma }^2}}$ ，分布函数则为： $\psi \left(kt|z\right)={\displaystyle {\int }_{-\infty }^{+\infty }{\text{e}}^{\frac{\mu \left(1-z\right)}{{\sigma }^2}}\cdot {\text{e}}^{\frac{kt\left(2\mu -kt-2\right)}{2{\sigma }^2}}\text{d}\left(kt\right)}={\text{e}}^{\frac{\mu \left(1-z\right)}{{\sigma }^2}}{\displaystyle {\int }_{-\infty }^{+\infty }{\text{e}}^{\frac{kt\left(2\mu -kt-2\right)}{2{\sigma }^2}}\text{d}\left(kt\right)}={\text{e}}^{\frac{\mu \left(1-z\right)}{{\sigma }^2}}{\displaystyle {\int }_{-\infty }^{+\infty }{\text{e}}^{\frac{kt\left(\mu -1\right)}{{\sigma }^2}}{\text{e}}^{{\left(kt\right)}^2\cdot -\frac{1}{2{\sigma }^2}}\text{d}\left(kt\right)}$ ，令 $\alpha =\frac{1}{2{\sigma }^2}$ ， $\beta =\frac{\mu -1}{{\sigma }^2}$ ，故原式的积分部分为高斯积分 $I\left(\alpha ,\beta \right)={\displaystyle {\int }_{-\infty }^{+\infty }{\text{e}}^{-\alpha {\left(kt\right)}^2+\beta kt}\text{d}\left(kt\right)}={\text{e}}^{\frac{{\beta }^2}{4\alpha }}\sqrt{\frac{\pi }{\alpha }}$ ， $\frac{{\beta }^2}{4\alpha }={\left(\frac{\mu -1}{{\sigma }^2}\right)}^2/\frac{2}{{\sigma }^2}=\frac{{\left(\mu -1\right)}^2}{2{\sigma }^2}$ ， $\sqrt{\frac{\pi }{\alpha }}=\sqrt{2\pi }\sigma$ ，所以 $I\left(\alpha ,\beta \right)=\sqrt{2\pi }\sigma \cdot {\text{e}}^{\frac{{\left(\mu -1\right)}^2}{2{\sigma }^2}}$ ，故 $\psi \left(kt|z\right)=\sqrt{2\pi }\sigma \cdot {\text{e}}^{\frac{{\mu }^2-2\mu z+1}{2{\sigma }^2}}$ ，磨耗量kt在Z条件下的分布函数同样是具有相关的正态特性，时间 是连续的，表面高度的磨耗率k在很大的程度上呈现正态分布规律。为将磨耗率k更加直观化，可从接触线质量、磨耗量与时间的关系探索出来。

如图5所示，接触线的质量为m，初始质量为 $m_0$ ，磨耗量为 $m^{\prime }$ ，初始磨耗量为0，恒有 $m+m^{\prime }=m_0$ ，由于 $m_0$ 是一个常数，故接触线质量的函数m与磨耗量的函数 $m^{\prime }$ 相互关联，同时进行变化，二者单调性相反。m只能单调递减，而 $m^{\prime }$ 只能单调递增。当 $m^{\prime }=0$ 时， $m=m_0$ ；当 $m^{\prime }=m_0$ 时， $m=0$ ；当 $m^{\prime }=m$ 时， $m^{\prime }+m^{\prime }=m_0$ ，所以 $m^{\prime }=m=\frac{1}{2}{m}_0$ 。可见，m与 $m^{\prime }$ 是关于直线 $M=\frac{1}{2}{m}_0$ 对称的，二者趋势为各自从两端逐渐向 $\frac{1}{2}{m}_0$ 靠近，并在 $t_0$ 时间点 $\frac{1}{2}{m}_0$ 处相交，之后m往0方向， $m^{\prime }$ 往 $m_0$ 方向发展。磨耗率 $k=\frac{m_0-m}{t}=\frac{m^{\prime }}{t}$ ，一般地，在某个时间 $\left(t_1,t_2\right)$ 区间内， $k=\left|\frac{m_2-m_1}{t_2-t_1}\right|=\frac{{m^{\prime }}_2-{m^{\prime }}_1}{t_2-t_1}$ ，故磨耗率可由接触线质量随时间的变化来表达，也可以用磨耗的变化量来表达。由于单调性相反，所以 $\frac{m_2-m_1}{t_2-t_1}=-\frac{{m^{\prime }}_2-{m^{\prime }}_1}{t_2-t_1}$ ，即 $m_2-m_1=-\left({m^{\prime }}_2-{m^{\prime }}_1\right)$ ， $\left|\Delta m\right|=\left|\Delta m^{\prime }\right|$ 。即使知道m与 $m^{\prime }$ 所具有的一些单调性变化，但是m与 $m^{\prime }$ 的变化规律是未知的，变化的快慢是随机的。k具有随机性且无记忆性，不随时间t的变化而变化，在每一段时间的区间内，k都是独立的，不受其他区间参数的影响。所以，关于磨耗变化的了解，在磨耗率k这一数据上，仅能以概率去构建模型，其分布呈现正态性质。

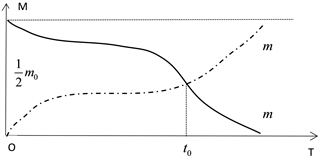
Figure 5. Relationship between the quality of contact wire body and wear quality

图5. 接触线本体质量与磨耗质量关系

在机械磨耗的随机模型的基础上，磨耗率的稳定性同样得到表征。磨耗率以正态分布的密度函数呈现，表明了微观层面上其变化是一个正态型的过程。又因磨耗率k不具有记忆性，故磨耗质量的变化规律在微观上呈现出随机性。那么，磨耗率是不具有稳定性的，其轨迹无统一的准线，不随某一特定值进行振荡。另一方面，从磨耗率的不稳定性反推出，现实中接触网系统的环境因素，只要产生微小的颤动，接触线运行时的磨耗率则会发生较大改变，也反映了磨耗变化的难以预测性、可控性。

6. 结语

弓网机械磨耗的相关参数十分复杂，以致机械磨耗现象趋于隐秘。本文尝试以数学语言将其机械磨耗进行描述，在理论框架内对其进行规范化、计量化。首先，确立接触线磨耗的本质与统一的量纲，对磨耗的研究实行规范化；其次，在宏观上推导出磨耗产生的相关理论公式，寻找出接触线产生磨耗的动力学原因；然后从微观上建立磨耗的随机模型，描述其随机性。结论总共有以下几点：

1) 磨耗的本质是接触线的变质量运动，量纲为质量[m]；

2) 磨耗的计算，应以求质量为方向，可推导出上文的标准计算公式；

3) 建立动力学模型，宏观上揭示出接触线产生磨耗(变质量)的深层原因，在于进动角 $\phi$ 的动能 $T_{\phi }$ 的存在，接触线本体的运动具有稳定性；

4) 建立随机模型，微观上揭示了磨耗率的随机性质，具有正态类型的行为，是不稳定的，解释现实中无法预测磨耗的原因。

当然，通过理论模型的构造，显现出弓网机械磨耗的一些的特性，旨在为实际的弓网机械磨耗的相关问题的解决、以及磨耗量变化的可控性提供理论参考，并使得地铁系统中接触线磨耗行为的理论研究得以进一步发展。