1. 引言
2020年7月新疆爆发二轮疫情。此次疫情以新疆乌鲁木齐为中心。自2020年7月16日以来,新疆乌鲁木齐新增新型冠状肺炎阳性患者,引起了公众和政府相关部门的广泛关注。2020年7月16日新疆第一例新增新型冠状肺炎阳性患者至2020年8月18日再无新增的阳性患者,新疆各级政府部门的有效管控和各方面的防控措施为新疆疫情的防治做出了重大贡献。
自疫情爆发以来国内外学者纷纷对新型冠状肺炎疫情相关情况进行大量研究。Munandar [1] 利用非齐次泊松过程对以“新型冠状病毒”为关键词的推文进行预测并计算了网民发布有关“新型冠状病毒”的推文数量的概率;Xiaolei Zhang等 [2] 采用分段泊松模型来分析七国集团六个西方国家每日“新型冠状病毒”新增病例数据并对转折点、持续时间和发病率进行统计预测;Y Ma,X Liu等 [3] 使用中国武汉以外的城市的案例数据建立了一个泊松线性混合效应模型用于估计武汉潜在病例数。
本文对泊松过程及复合泊松过程的基本特性进行介绍,利用泊松过程对2020年7月16日至2020年8月17日期间新疆新型冠状肺炎阳性患者病例数进行计算分析,基于复合泊松过程建立阳性患者相关花费的数学模型。本文所得结论对新疆相关部门今后如何科学地投资医疗资源,合理地实行疫情防控管理等问题提供一定的参考依据。
2. 预备知识
定义1.1 [4] 称计数过程
,为具有参数
的泊松过程,如果
满足下列条件:
1)
。
2)
是独立增量过程。
3)
是平稳增量过程,并且
,
。
定理1.1 [5] 强度为
的泊松过程
,它的到达事件的间隔序列
是相互独立的随机变量序列,则
是独立同分布的均值为
的指数分布。
定理1.2 [6] 设
是与泊松过程
对应的一个等待时间序列,其中
,则
服从参数为n和
的伽玛分布。
定义1.2 [5] 设
是参数为
的泊松过程,若
其中
为独立同分布随机变量序列且与
独立,则称
为复合泊松过程。
3. 主要结论
定理2.1设
是参数为
的泊松过程,则:
1) 均值函数为
。
2) 方差函数为
。
证明:1)
,
用同样的方法可以得到
。
2)
。
定理2.2 若
是参数为
的泊松过程,且
,则复合泊松过程
具有如下数字特征:
1) 特征函数为
,其中
是随机变量
的特征函数;
表示速率。
2) 均值函数为
。
3) 方差函数为
。
证明:1)
,
由于
与
,是相互独立的,则:
2) 由特征函数与矩的关系可得数学期望为:
,
因为
,所以
。
3) 均方值为
故
。
4. 实证分析
4.1. 数据统计
本研究从新疆维吾尔自治区卫生健康委员会官方网站收集了2020年7月16日至2020年8月17日新型冠状肺炎的每日患病数据(本文使用的数据暂不考虑2020年7月15日之前的病例),并利用Excel绘制统计图如图1:
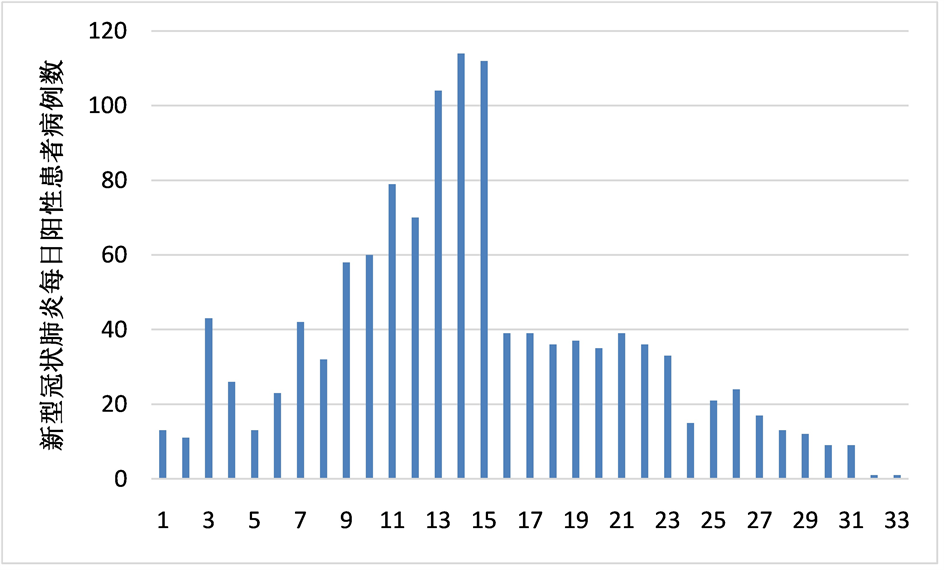
Figure 1. Daily number of COVID-19 positive patients in Xinjiang
图1. 新疆新型冠状肺炎每日阳性患者病例数
根据图1可以发现新疆新型冠状肺炎阳性患者的病例数有较大的波动,在2020年7月28日(第13天)新疆新型冠状肺炎阳性患者人数明显增加达到104人,在7月31日(第16天)新型冠状肺炎患者大幅减少,达到39人。
表1列出了新疆2020年7月16日至8月17日新疆新型冠状肺炎患者的描述性统计数据:

Table 1. Descriptive statistics of daily cases of COVID-19 positive patients
表1. 新型冠状肺炎阳性患者每日病例的描述性统计量
根据表1,2020年7月16日至8月17日新疆新型冠状肺炎阳性患者的平均每日病例数约为37人。新型冠状肺炎阳性患者病例最多人数发生在7月29日。多达114人,在此之后每日的病例数逐渐减少。
4.2. 新疆新型冠状肺炎阳性患者每日病例数的泊松过程
新疆每日阳性患者病例遵循泊松过程。由泊松过程的特性计算得到每日阳性患者的发生率为:
人每天。
也就是说在2020年7月16日至2020年8月17日期间新疆平均每天大约会有37名新型冠状肺炎阳性患者。
从2020年7月16日至2020年8月17日新疆每日的新型冠状肺炎阳性患者病例数的期望和方差分别为:
.
.
从2020年7月16日至2020年8月17日,新疆新型冠状肺炎阳性患者的平均人数为1216人,方差为1216。从2020年7月16日至2020年8月17日新疆新型冠状肺炎阳性患者病例数为1216人。利用泊松过程的特性我们得到,从2020年7月16日至2020年8月17日新疆没有新型冠状肺炎阳性患者病例的概率为:
.
.
由此可见,从2020年7月16日至2020年8月17日新疆没有新型冠状肺炎阳性患者病例的概率是非常小的。
4.3. 新疆新型冠状肺炎阳性患者每日花费的复合泊松过程
令
表示每位新型冠状肺炎阳性患者的花费(包括医疗费及餐食,住宿等),则从2020年7月16日至2020年8月17日期间新疆新型冠状肺炎阳性患者的总花费可看成一个复合泊松过程
。
由复合泊松过程的特性可得:
。
因此,利用所得结论我们可以得到从2020年7月16日到2020年8月17日为止新疆新型冠状肺炎阳性患者的平均花费。
4.4. 小结
从2020年7月16日起新疆出现新增新型冠状肺炎阳性患者到2020年8月17日为止新疆无新增病例。在此期间,新疆新型冠状肺炎阳性患者的平均病例数约为37人,且没有新型冠状肺炎阳性患者的概率非常小。因此,公众应该始终意识到新型冠状病毒的传播。
5. 结束语
本文对泊松过程和复合泊松过程的相关知识进行介绍,应用泊松过程和复合泊松过程的知识对新疆2020年7月的新型冠状肺炎阳性患者病例数及花费情况进行分析。计算出了在此期间新疆新型冠状肺炎阳性患者病例数的平均病例
,得到相应的新型冠状肺炎阳性患者花费的数学模型。根据文章的分析,帮助政府及相关部门实施不同的防控措施以有效减少新型冠状病毒的传播。