双馈异步风力发电机的矢量控制

Vector Control of Doubly-Fed Asynchronous Wind Generator

摘要: 本文通过研究双馈异步风力发电机的控制策略，来实现双馈风力发电机的变速恒频，并对其运行过程进行仿真分析。文中根据建立的双馈风力发电机数学模型研究其控制策略，本文研究的是转子侧基于定子电压定向的控制策略，对双馈异步风力发电机定子侧输出的有功和无功功率进行解耦控制。和转子侧基于定子磁链定向的控制策略相比，这种控制方法减少了定子磁链的计算，减小了误差。通过此控制方式，使用Matlab/Simulink软件搭建了双馈异步风力发电机的仿真模型，通过仿真验证了该控制策略可以有效地对有功和无功进行独立控制。

Abstract: In this paper, by studying the control strategy of doubly-fed asynchronous wind generator, the var-iable speed and fixed frequency of doubly-fed wind generator is realized, and its operation process is simulated and analyzed. In this paper, the control strategy of doubly-fed wind turbine is studied according to the established mathematical model, and the rotor-side control strategy based on sta-tor voltage orientation is studied to decouple the effective and reactive power output of doubly-fed asynchronous wind turbine. Compared with the control strategy based on stator flux orientation on the rotor side, this control method reduces the calculation of stator flux and reduces the error. Through this control mode, the simulation model of doubly-fed asynchronous wind generator is es-tablished by using Matlab/Simulink software. The simulation results show that the control strategy is effective and effective and can control reactive power independently.

1. 引言

为了早日实现碳达峰和碳中和的目标，并确保满足人类经济社会的电力需求，需要最大化利用新能源 [1] [2] 。而新能源发电中，风力发电和光伏发电占比较大 [3] 。风电作为一类重要的新能源发电形式，逐渐在电力系统中占据重要地位。由于风能是一种随机性，不稳定的资源，因此双馈风机并网时的电能是波动的。并网时风机输出功率波动会造成电网电压波动，引发停电事故 [4] [5] 。由于现在新能源发电并网，其中大量的电力电子器件对电网的频率变化较为敏感。因此，对风力发电并网时输出频率提出了更高的要求 [6] 。在变速恒频风力发电技术成熟后，矢量控制技术广泛应用于变速恒频发电系统中。采用矢量控制可按照捕获最大风能的要求在风速变化的情况下实时地调节风力机转速，实现风力机组最大功率追踪，保证了功率输出的稳定 [7] ，提高了发电机组的运行效率；双馈风力发电机控制系统通过改变转子侧励磁电流的幅值、频率以及相位角实现输出电能的恒频恒压，并且对双馈异步风力发电机的有功和无功功率进行了解耦控制。采用矢量控制技术提高了风力发电系统的动态稳定性和静态稳定性，让双馈风力发电系统实现了柔性并网 [8] [9] 。

2. 双馈发电系统的工作原理

2.1. 双馈异步风力发电机的变速恒频原理

风速变化时，为了保持定子侧输出频率和电网频率相同，可以调节转子侧的励磁电流的频率。双馈异步风力发电机的定子侧和电网直接相连，转子侧通过两个变流器和变压器等与电网相连。定子的旋转磁场角速度为 ${\omega }_m=2\pi f_1$ ， $f_1$ 为电网频率，若转子励磁电流频率为 $f_r$ ，电机转子转速为 $n_r$ ，为了保证变速恒频，上述提到的变量应该满足公式(1)：

$f_1=\frac{n_p{n}_r}{60}+f_r$ (1)

式中 $n_p$ 为极对数。

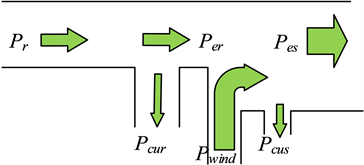
当外界风速改变时，通过上述公式可知改变转子励磁电流的频率可以维持定子侧输出的频率稳定。保证双馈异步风力发电机的稳定运行。同步发电时定子旋转磁场速度等于转子机械旋转速度，给转子通入直流电，在亚同步发电时，给转子通入正相序电流，使转子磁场的旋转速度等于定子磁场旋转速度，超同步发电时候，给转子通上反相序的电流，使转子磁场速度等于定子磁场旋转速度。在变速恒频 [8] 的不同工况下，功率流向如下图所示。

三种典型工作状态(亚同步、同步、超同步速)下，系统有功功率流向如图1所示：

(a) 亚同步运行(s < 0) (b) 超同步运行(s > 0) (c) 同步运行(s = 0)

Figure 1. Active power flow chart

图1. 有功功率流向图

2.2. 双馈异步风力发电机的等效模型

为了便于分析和建模，还常将电机模型看作理想状态 [10] 。理想状态下双馈异步风力发电机绕线物理模型如图2所示：

Figure 2. DFIG equivalent circuit model

图2. DFIG等效电路模型

这样，三相坐标系下方程可表示如下

电压方程为

$\{\begin{array}{l}{u}_{sA}=R_s{i}_{sA}+\frac{\text{d}{\psi }_{sA}}{\text{d}t}\\ u_{sB}=R_s{i}_{sB}+\frac{\text{d}{\psi }_{sB}}{\text{d}t}\\ u_{sC}=R_s{i}_{sC}+\frac{\text{d}{\psi }_{sC}}{\text{d}t}\end{array}$ (2)

$\{\begin{array}{l}{u}_{ra}=R_r{i}_{ra}+\frac{\text{d}{\psi }_{ra}}{\text{d}t}\\ u_{rb}=R_r{i}_{rb}+\frac{\text{d}{\psi }_{rb}}{\text{d}t}\\ u_{rc}=R_r{i}_{rc}+\frac{\text{d}{\psi }_{rc}}{\text{d}t}\end{array}$ (3)

为了简洁，式中 $u_{sA},u_{sB},u_{sC},u_{ra},u_{rb},u_{rc}$ 为定转子相电压， $i_{sA},i_{sB},i_{sC},i_{ra},i_{rb},i_{rc}$ 分别为定转子相电流， ${\psi }_{sA},{\psi }_{sB},{\psi }_{sC},{\psi }_{ra},{\psi }_{rb},{\psi }_{rc}$ 分别为定转子磁链； $R_s,R_r$ 为定转子电阻。

矩阵形式的磁链方程为

$\psi =\left(\begin{array}{c}{\psi }_s\\ {\psi }_s\end{array}\right)=\left(\begin{array}{cc}{L}_{ss}& L_{ss}\\ L_{rs}& L_{rr}\end{array}\right)\left(\begin{array}{c}{i}_s\\ i_r\end{array}\right)$ (4)

式中

${\psi }_s={\left[{\psi }_{sA},{\psi }_{sB},{\psi }_{sC}\right]}^{\text{T}},{\psi }_r={\left[{\psi }_{ra},{\psi }_{rb},{\psi }_{rc}\right]}^{\text{T}},i_s={\left[i_{sA},i_{sB},i_{sC}\right]}^{\text{T}},i_r={\left[i_{ra},i_{rb},i_{rc}\right]}^{\text{T}}$

$L_{ss}=\left(\begin{array}{ccc}{L}_{ms}+L_{ls}& -0.5L_{ms}& -0.5L_{ms}\\ -0.5L_{ms}& L_{ms}+L_{ls}& -0.5L_{ms}\\ -0.5L_{ns}& -0.5L_{ms}& L_{ms}+L_{ls}\end{array}\right),L_{rr}=\left(\begin{array}{ccc}{L}_{mr}+L_{lr}& -0.5L_{mr}& -0.5L_{mr}\\ -0.5L_{mr}& L_{mr}+L_{lr}& -0.5L_{mr}\\ -0.5L_{mr}& -0.5L_{mr}& L_{mr}+L_{lr}\end{array}\right),$

$L_{sr}=L_{rs}^{\text{T}}=L_{ms}\left(\begin{array}{ccc}\cos {\theta }_r& \cos \left({\theta }_r-{120}^{\circ }\right)& \cos \left({\theta }_r+{120}^{\circ }\right)\\ \cos \left({\theta }_r+{120}^{\circ }\right)& \cos {\theta }_r& \cos \left({\theta }_r-{120}^{\circ }\right)\\ \cos \left({\theta }_r-{120}^{\circ }\right)& \cos \left({\theta }_r+{120}^{\circ }\right)& \cos {\theta }_r\end{array}\right)$

$L_{sr}$ 和 $L_{rs}$ 互为转置矩阵，式中， $L_{ms}$ 为与定子一相绕组交链的最大互感磁通所对应的定子互感值；

$L_{mr}$ 为与转子一相绕组交链的最大互感磁通所对应的转子互感值，由于折算后定转子匝数相等，且 $L_{ms}=L_{mr}$ ； $L_{ls},L_{lr}$ 分别为定转子漏电感。

电磁转矩公式如下

$\begin{array}{c}{T}_e=-n_p{L}_m[\left(i_{sA}{i}_{ra}+i_{sB}{i}_{rb}+i_{sC}{i}_{rc}\right)\sin {\theta }_r+\left(i_{sA}{i}_{ra}+i_{sB}{i}_{rc}+i_{sC}{i}_{rc}\right)\sin \left({\theta }_r+{120}^{\circ }\right)\\ +\left(i_{sA}{i}_{ra}+i_{sB}{i}_{rb}+i_{sC}{i}_{rc}\right)\sin \left({\theta }_r-{120}^{\circ }\right)]\end{array}$ (5)

运动方程为

$T_e-T_L=\frac{J}{n_p}\frac{\text{d}{\omega }_r}{\text{d}t}$ (6)

式中 $T_e$ 为发电机的电磁转矩； $T_L$ 为风力机输出转矩；J为风电机组的转动惯量； ${\omega }_r$ 为转子角速度； n_p为极对数。

以此可构成一组三相坐标系中的DFIG模型。这个模型具有强耦合、非线性的性质，通过变换到旋转坐标系来简化坐标变换的运算。旋转坐标系下磁链方程

$\{\begin{array}{c}{\psi }_{sd}=L_s{i}_{sd}+L_m{i}_{rd}\\ {\psi }_{sq}=L_s{i}_{sq}+L_m{i}_{rq}\\ {\psi }_{rd}=L_r{i}_{rd}+L_m{i}_{sd}\\ {\psi }_{rq}=L_r{i}_{rq}+L_m{i}_{sq}\end{array}$ (7)

式中 $L_m$ 为旋转坐标系下的等效互感，且 $L_m=1.5L_{sm}=1.5L_{rm}$ ； $L_s$ 为旋转坐标系下的定子自感，且 $L_s=1.5L_{sm}+L_{ls}=L_m+L_{ls}$ ； $L_r$ 为旋转坐标系下的转子自感，且 $L_r=1.5L_{rm}+L_{lr}=L_m+L_{lr}$ 。旋转坐标系下的电压方程为

$\{\begin{array}{l}{u}_{sd}=R_s{i}_{sd}+\frac{\text{d}{\psi }_{sd}}{\text{d}t}-{\omega }_s{\psi }_{sq}\\ u_{sq}=R_s{i}_{sq}+\frac{\text{d}{\psi }_{sq}}{\text{d}t}+{\omega }_s{\psi }_{sd}\end{array}$ (8)

$\{\begin{array}{l}{u}_{rd}=R_r{i}_{rd}+\frac{\text{d}{\psi }_{rd}}{\text{d}t}-{\omega }_{sl}{\psi }_{rq}\\ u_{rq}=R_r{i}_{rq}+\frac{\text{d}{\psi }_{rq}}{\text{d}t}+{\omega }_{sl}{\psi }_{rd}\end{array}$ (9)

电磁转矩方程

$T_e=n_p{L}_m\left(i_{sq}{i}_{rd}-i_{sd}{i}_{rq}\right)$ (10)

3. 控制策略

双馈发电机的转子电流矢量控制可分为定子磁链定向 [11] 与定子电压定向两种。定子磁链定向和定子电压定向对比如下：

1) 定子磁链定向控制其磁链计算不仅需要测量电压还需要电流，定子电压定向只需测量电压量。

2) 直接测量磁链是不容易的，电压和电流的测量误差都会导致磁链的不准确，对比电压测量相对容易。

3) 电机是感性负载，采样噪声、电机参数等误差的引入，会导致气隙磁链出现误差，进而导致磁链位置角度误差，角度误差进一步放大气隙磁链误差，容易导致计算发散。

定子电压定向和定子磁链定向相比，定子电压定向减少了定子磁链的观测，减少了由于电机特性而造成的磁链误差；而且与网侧变流器的控制方法相似，简化了背靠背变流器的整体控制系统结构；故本文转子侧变流器的控制策略采用定子电压定向的设计。

由于双馈电机的定子侧和电网电压直接相连，电压、幅值和频率都要保持不变，且定子电阻相对于电网可以忽略，则有

$\frac{\text{d}}{\text{d}t}{\psi }_{sd}=0,\frac{\text{d}}{\text{d}t}{\psi }_{sq}=0,R_s=0$ (11)

采用矢量控制将定子电压定向在q轴时

$u_{sq}=U_s,u_{sd}=0$ (12)

$P_s=U_s{i}_{sq},Q_s=U_s{i}_{sd}$ (13)

式(12)表明转子电流分量i_q控制有功功率P_s，转子电流分量i_d控制无功功率Q_s。

把式(7) (11)代入式(9)得转子电压方程为

$\{\begin{array}{l}{u}_{rq}=\left(R_r+\frac{L_m^2}{L_s^2}{R}_s\right)i_{rq}+\left(L_r-\frac{L_m^2}{L_s}\right)\frac{\text{d}{i}_{rq}}{\text{d}t}+\frac{L_m}{L_s}{u}_s-\frac{L_m}{L_s}\left(\frac{R_s}{L_s}{\psi }_{sq}+{\omega }_r{\psi }_{sd}\right)+{\omega }_{sl}\left(L_r-\frac{L_m^2}{L_s}\right)i_{rq}\\ u_{rd}=\left(R_r+\frac{L_m^2}{L_s^2}{R}_s\right)i_{rd}+\left(L_r-\frac{L_m^2}{L_s}\right)\frac{\text{d}{i}_{rd}}{\text{d}t}-\frac{L_m}{L_s}\left(\frac{R_s}{L_s}{\psi }_{sd}+{\omega }_r{\psi }_{sq}\right)-{\omega }_{sl}\left(L_r-\frac{L_m^2}{L_s}\right)i_{rq}\end{array}$ (14)

对式(14)中的转子电流分量动态项PI调节后可得到

$\{\begin{array}{l}{u}_{rq}^{\ast }=\left(K_{irp}+\frac{K_{irl}}{s}\right)\left(i_{rq}^{\ast }-i_{rq}\right)+u_{rqc}\\ u_{rd}^{\ast }=\left(K_{irP}+\frac{K_{irl}}{s}\right)\left(i_{rd}^{\ast }-i_{rd}\right)-u_{rdc}\end{array}$ (15)

据此可构建基于定子电压定向的双馈异步风力发电机机侧矢量控制框图，其控制结构如图3所示：

Figure 3. Control block diagram

图3. 控制框图

4. 双馈异步风力发电机矢量控制仿真研究

4.1. 系统仿真参数

电网电压设置为690 V，设置电网频率为50赫兹；网侧变流器：电感设置为0.5 mH，直流母线：设置电压为1200 V。

双馈异步风力发电机：设置额定功率1500 kw，定子电压690 V，频率50 Hz，电阻5.5 mΩ，电感0.156 mH，转子电阻6.21 mΩ，电感0.226 mH，电感11.01 mH，极对数设置为2。叶轮直径设置为66 m，额定风速11.5 m/s。

4.2. 不同运行状态下的系统仿真

仿真方案一：

转子侧变流器的输出有功功率参考量P*由风力机提供，无功功率参考值为0，在仿真到1.5 s时风速从10 m/s增加到11.6 m/s，有功指令值改变仿真结果如图4所示：

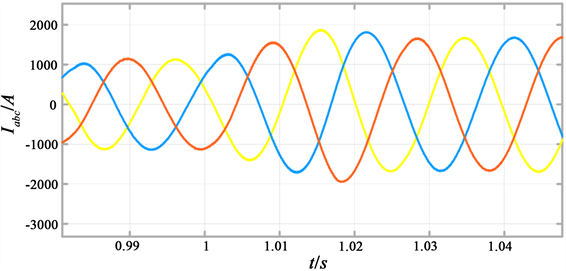(a) 定子侧输出电流波形 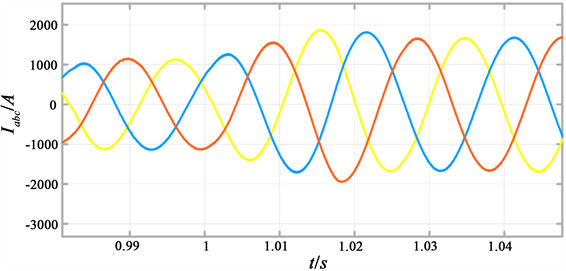(b) 转子电流分量波形图 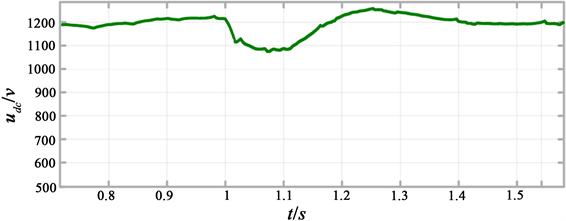(c) 母线电压波形 (d) 功功率波形图

Figure 4. Change the active power simulation diagram

图4. 改变有功仿真图

仿真方案二：

有功指令值保持不变，无功功率在仿真1 s时，增加为0.3兆瓦，改变无功仿真图如图5所示：

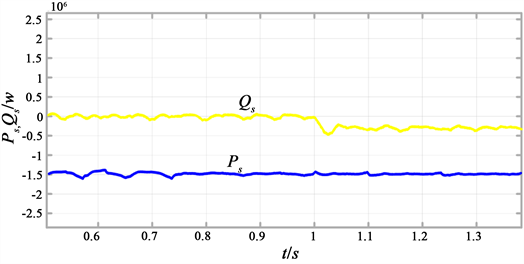(a) 功率波形图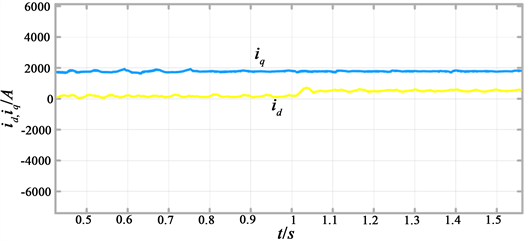(b) 转子电流分量波形图

Figure 5. Change the reactive power simulation diagram

图5. 改变无功仿真图

由仿真结果可知，风速10 m/s时，风机输出有功功率指令为值为1兆瓦，外环有功功率跟踪最大功率也稳定在1兆瓦左右，直流母线电压经过调整之后保持稳定在1200 V，无功功率和无功电流分量保持在0左右。当风速在1.5 s时增加到额定风速时，风机输出有功功率指令值达到额定功率1.5兆瓦，转子q轴电流分量增加，控制外环功率稳定在1.5兆瓦左右，无功功率和无功电流分量也保持不变。达到了对有功与功功率的独立控制的目的。

由仿真结果可知，有功功率保持不变，在1 s时无功功率给定值Q*增加到0.3兆瓦，无功电流分量i_rq迅速增加，控制无功电流Q增加，稳定在0.3兆瓦左右。在此期间，有功功率保持不变，达到了对有功与功功率的独立控制的目的。

5. 结论

从上述两个方案的仿真结果可知，方案一在1.5 s时增加有功功率指令值，无功功率指令值保持不变时，电流有功分量控制定子输出有功功率快速跟随有功功率指令值，定子输出无功功率不变；方案二在1 s时增加无功功率指令值，有功功率指令值保持不变，转子电流无功分量控制无功功率快速跟随无功功率指令值，定子输出有功功率不变。两个方案证明该控制策略达到了对有功功率和无功功率解耦控制的目的。当机侧有功和无功功率改变时，网侧直流母线电压都能快速调节保持稳定在1200 V，网侧电压波形保持稳定，说明了网侧和机侧的变流器控制相对独立，通过上述波形图分析，转子侧基于定子电压定向的控制策略可有效实现双馈异步风力发电机的解耦控制和正常运行输出。

NOTES

^*通讯作者。