构造中点模型解析中考几何试题的研究

Research on the Construction of Mid-Point Model to Analyze the Geometry Test Questions of Senior High School Entrance Examination

摘要: 文章通过归纳总结常见几种中点模型，并从近几年通过构造中点模型求解的中考几何压轴试题出发，对其分析、解答和小结给予展示，并提出相应的解题技巧和教学思考，以期让学生找到解决此类问题的解题思路，开拓几何思维，培养学生的问题解决能力。

Abstract: By summarizing several common midpoint models, and starting from the geometric final exami-nation questions of the senior high school entrance examination solved by constructing the mid-point model in recent years, this paper shows its analysis, solution and summary, and puts forward the corresponding problem-solving skills and teaching thinking, so as to enable students to find the problem-solving ideas to solve such problems, develop geometric thinking and cultivate students’ problem-solving ability.

1. 引言

构造几何模型是学生学习和运用的难点 [1] ，在中考几何压轴试题的解答中往往逃避不了模型的运用。中点模型就是几何模型中的一种。初中数学中存在四个常见的中点模型，即全等三角形八字模型、等腰三角形三线合一模型、三角形中位线定理模型、直角三角形斜边中线定理模型。中点是指将一条线段分为两条相等线段的点，是几何常见的特殊点之一，在中考几何压轴试题中经常出现一些与中点相关的问题，解答时若能灵活运用中点来添加辅助线构造相应的中点模型，往往可以达到良好的解题效果。但是与中点相关的问题涉及的内容跨章节，甚至跨年级，加之添加辅助线的方法灵活多变，教师教起来困难，学生学起来也不易 [2] 。为此，文章通过归纳总结常见几种中点模型，并从近几年通过构造中点模型求解的中考几何压轴试题出发，挖掘题目中的中点模型，探究其典型解法，以期让学生找到解决此类问题的解题思路，并帮助学生熟练掌握常见几种中点模型，丰富知识结构，促进几何思维的发展，提升综合运用知识的能力、分析和解决问题的能力、逻辑推理能力以及直观想象能力，进而提升数学学科核心素养。

2. 中点模型归纳

2.1. 全等三角形八字模型(倍长中线模型)

当出现三角形的中线或中点时，常常将此中线或类中线(与中点有关的线段)延长一倍构造全等三角形。目的是利用全等三角形的性质实现相等的线段和相等的角度的转化，即对已知条件中的线段和角度进行转移。

【模型解读】如图1，在 $\Delta ABC$ 中，AD是BC边的中线，延长AD至点E，使 $DE=AD$ ，连接BE，则有 $\Delta ADC\cong \Delta EDB$ 。如图2，在 $\Delta ABC$ 中，点D是BC边的中点，延长FD至点E，使 $DE=FD$ ，连接CE，则有 $\Delta FDB\cong \Delta EDC$ 。

Figure 1. Double long midline

图1. 倍长中线

Figure 2. Double-long class midline

图2. 倍长类中线

2.2. 等腰三角形三线合一模型

当出现等腰三角形时，常隐含有底边中点，将其与顶角的顶点连接，可构成等腰三角形的三线合一 [3] 。目的是利用等腰三角形三线合一性质证明相等的线段或相等的角度、两条直线的垂直关系以及半角倍角。“三线合一”即在等腰三角形中顶角的角平分线、底边上的中线、底边上的高线互相重合为一条线。

【模型解读】如图3，在等腰 $\Delta ABC$ 中，点D是底边BC上的中点，连接AD，则有 $BD=CD$ ， $\angle BAD=\angle CAD$ ， $AD\perp BC$ 。

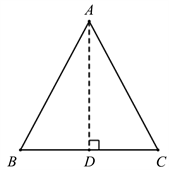
Figure 3. Isosceles triangle three-in-one model

图3. 等腰三角形三线合一模型

2.3. 三角形中位线定理模型

当同时出现多条边的中点时，常常构造三角形的中位线；或当出现一个中点，要求证明线段平行或倍分关系时，也常常构造三角形的中位线。目的是利用三角形中位线定理得到线段位置上的“平行”和数量上的“倍分”关系，并得到相似三角形进而得到相关线段长的比例关系。“三角形中位线定理”即三角形的中位线平行于第三边(不与中位线接触)，并且等于第三边的一半。

【模型解读】如图4，在 $\Delta ABC$ 中，点D是AB边的中点，点E是AC边的中点，连接DE，则有

$DE\parallel BC$ ， $DE=\frac{1}{2}BC$ 。

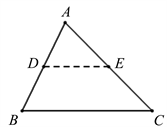
Figure 4. Triangle median line theorem model

图4. 三角形中位线定理模型

2.4. 直角三角形斜边中线定理模型

当出现直角三角形斜边中点时，常常会作斜边上的中线。目的是利用直角三角形斜边中线定理，构建相应地等腰三角形获得相等的线段、相等的角度等。“直角三角形斜边中线定理”即直角三角形斜边上的中线等于斜边的一半。

【模型解读】如图5，在 $Rt\Delta ABC$ 中，点D是斜边AC上的中点，连接BD，则有

$AD=CD=BD=\frac{1}{2}AC$ 。

Figure 5. Right triangle diagonal midline theorem model

图5. 直角三角形斜边中线定理模型

3. 中点模型解题示例

例1 (2020年北京中考第27题)在 $\Delta ABC$ 中， $\angle C={90}^{\circ }$ ， $AC>BC$ ，D是AB的中点。E为直线AC上一动点，连接DE，过点D作 $DF\perp DE$ ，交直线BC于点F，连接EF。1) 略；2) 当点E在线段CA的延长线上时，依题意补全图6，用等式表示线段AE，EF，BF之间的数量关系，并证明。

Figure 6. Question (2) the original graph

图6. 第(2)问原图

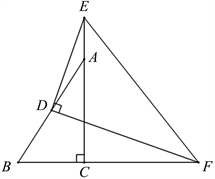
Figure 7. Question (2) completion graph

图7. 第(2)问补全图

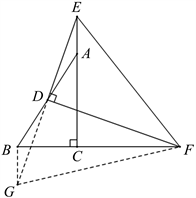
Figure 8. Construct a congruent triangle eight-character model

图8. 构造全等三角形八字模型

【分析】此题对应全等三角形八字模型。由于AE，EF，BF比较分散，所以无法证明它们之间的数量关系，但是可以通过移动边的位置，使AE，EF，BF在位置上产生关联，进而证明它们之间的数量关系。因为D是AB的中点，由此可将DE延长一倍，构造全等三角形八字模型，得到两个全等三角形，实现相等的线段和相等的角度的转化，便可实现移动边的位置，即 $GD=ED$ ， $BG=AE$ ，进而可得DF是EG的垂直平分线，所以 $GF=EF$ ，因此将比较分散的AE，EF，BF转移到了同一个直角三角形中，利用勾股定理，即可求解。

【解】依题意补全图6得到上图7。 $A{E}^2+B{F}^2=E{F}^2$ 。证明：如图8所示，延长ED至点G，使得 $GD=ED$ ，连接GB、GF，在 $\Delta BDG$ 和 $\Delta ADE$ 中， $GD=ED$ ， $\angle GDB=\angle EDA$ ， $BD=AD$ ，所以 $\Delta BDG\cong \Delta ADE$ ，所以 $BG=AE$ ， $\angle DGB=\angle DEA$ ，所以 $BG\parallel CE$ ，因为 $BG\parallel CE$ ， $\angle C={90}^{\circ }$ ，所以 $\angle GBF={90}^{\circ }$ ，又因为 $DF\perp DE$ ， $GD=ED$ ，所以 $GF=EF$ ，在 $Rt\Delta GBF$ 中，由勾股定理，得 $B{G}^2+B{F}^2=G{F}^2$ ，所以 $A{E}^2+B{F}^2=E{F}^2$ 。

【小结】本题解题的关键是构造全等三角形八字模型，利用全等三角形的判定、全等三角形的性质、两直线平行的判定、两直线平行的性质、垂直平分线的性质和勾股定理知识来解答。

例2 (2022年贵州铜仁中考第14题)如图9，四边形ABCD为菱形， $\angle ABC={80}^{\circ }$ ，延长BC到E，在 $\angle DCE$ 内作射线CM，使得 $\angle ECM={30}^{\circ }$ ，过点D作 $DF\perp CM$ ，垂足为F。若 $DF=\sqrt{6}$ ，则BD的长为____(结果保留根号)。

Figure 9. Example 2 original picture

图9. 例2原图

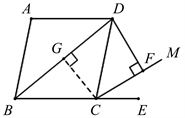
Figure 10. Construct an isosceles triangle three-in-one model

图10. 构造等腰三角形三线合一模型

【分析】此题对应等腰三角形三线合一模型。因为四边形ABCD为菱形，所以 $BC=CD$ ，所以 $\Delta BCD$ 为等腰三角形，由此可过点C作 $CG\perp BD$ ，垂足为点G，构造等腰三角形三线合一模型，可得点G为BD的中点，进而利用全等三角形的判定定理AAS，即可求解。

【解】因为四边形ABCD为菱形， $\angle ABC={80}^{\circ }$ ，所以 $BC=CD$ ， $\angle DCE={80}^{\circ }$ ， $\angle ADC={80}^{\circ }$ ， $\angle BDC={40}^{\circ }$ ，因为 $\angle ECM={30}^{\circ }$ ，所以 $\angle DCF={50}^{\circ }$ ，又因为 $DF\perp CM$ ，所以 $\angle FDC={40}^{\circ }$ ，过点C作 $CG\perp BD$ ，垂足为点G，如图10所示，因为 $BC=CD$ ， $CG\perp BD$ ，所以点G是BD的中点，在 $\Delta DCG$ 和 $\Delta DCF$ 中， $\angle DGC=\angle DFC={90}^{\circ }$ ， $\angle GDC=\angle FDC={40}^{\circ }$ ， $DC=DC$ ，所以 $\Delta DCG\cong \Delta DCF$ ，所以 $DG=DF$ ，所以 $BD=2DG=2DF=2\sqrt{6}$ ，所以 $BD=2\sqrt{6}$ 。

【小结】本题解题的关键是构造等腰三角形三线合一模型，利用菱形的性质、全等三角形的判定、全等三角形的性质和等腰三角形三线合一性质知识来解答。

例3 (2021年北京中考第27题)如图11，在 $\Delta ABC$ 中， $AB=AC$ ， $\angle BAC=\alpha$ ，M为BC的中点，点D在MC上，以点A为中心，将线段AD顺时针旋转 $\alpha$ 得到线段AE，连接BE，DE。1) 略；2) 过点M作AB的垂线，交DE于点N，用等式表示线段NE和ND的数量关系，并证明。

Figure 11. Example 3 original picture

图11. 例3原图

【分析】此题对应三角形中位线定理模型。因为M为BC的中点，因此可以过点E作 $EG\parallel MN$ 交BC于点G，构成三角形的中位线基本图形，进而利用三角形中位线定理，即可求解。

【解】 $NE=ND$ 。证明：如图12所示，过点E作 $EG\parallel MN$ 交BC于点G，交AB于点O，因为 $MN\perp AB$ ，所以 $EG\perp AB$ 于点O，在 $\Delta ABC$ 中， $AB=AC$ ，所以 $\angle ABC=\angle ACB$ ，因为线段AD顺时针旋转 $\alpha$ 得到线段AE， $\angle BAC=\alpha$ ，所以 $AE=AD$ ， $\angle EAD=\alpha$ ，所以 $\angle EAB+\angle BAD=\angle DAC+\angle BAD=\alpha$ ，所以 $\angle EAB=\angle DAC$ ，在 $\Delta ABE$ 和 $\Delta ACD$ 中， $AE=AD$ ， $\angle EAB=\angle DAC$ ， $AB=AC$ ，所以 $\Delta ABE\cong \Delta ACD$ ，所以 $BE=CD$ ， $\angle ABE=\angle ACB$ ，因为 $\angle ABC=\angle ACB$ ，所以 $\angle ABE=\angle ABC$ ，在 $\Delta OBE$ 和 $\Delta OBG$ 中，因为 $\angle EOB=\angle GOB={90}^{\circ }$ ， $BO=BO$ ， $\angle OBE=\angle OBG$ ，所以 $\Delta OBE\cong \Delta OBG$ ，所以 $BE=BG$ ，因为 $BE=BG$ ， $BE=CD$ ，所以 $BG=CD$ ，又因为M为BC的中点，所以 $MG=MD$ ，即M为DG的中点，因为 $EG\parallel MN$ ，所以MN为 $\Delta EGD$ 的中位线，所以N为ED的中点，所以 $NE=ND$ 。

Figure 12. Construct triangle median line theorem model

图12. 构造三角形中位线定理模型

【小结】本题解题的关键是构造三角形中位线定理模型，利用全等三角形的判定、全等三角形的性质和三角形中位线定理知识来解答。

例4 (2020年浙江温州中考第22题)如图13，C，D为 $\odot O$ 上两点，且在直径AB两侧，连结CD交AB于点E，G是 $\stackrel{⌢}{AC}$ 上一点， $\angle ADC=\angle G$ 。1) 略；2) 点C关于DG的对称点为F，连结CF。当点F

落在直径AB上时， $CF=10$ ， $\tan \angle 1=\frac{2}{5}$ ，求 $\odot O$ 的半径。

Figure 13. Example 4 original picture

图13. 例4原图

【分析】此题对应直角三角形斜边中线定理模型。因为 $\angle ADC=\angle G$ ，AB为 $\odot O$ 的直径，所以 $AB\perp CD$ ， $\Delta ECF$ 为直角三角形，E为CD的中点。又因为点C，F关于DG对称，所以 $DG\perp CF$ ， $\Delta HCD$ 为直角三角形，H为CF的中点。出现两个直角三角形斜边中点，因此可连接EH构造两个直角三角形斜边中线定理模型( $Rt\Delta ECF$ 与 $Rt\Delta HCD$ )，即可求解。

【解】因为 $\angle ADC=\angle G$ ，所以 $\stackrel{⌢}{AC}=\stackrel{⌢}{AD}$ ，又因为AB为 $\odot O$ 的直径，所以 $AB\perp CD$ ， $CE=ED$ ，E为CD的中点，令CF与DG的交点为H，因为点C，F关于DG对称，所以 $DG\perp CF$ ，H为CF的中点，

连接EH，如图14所示，得到 $EH=\frac{1}{2}CF=\frac{1}{2}CD$ ，所以 $CD=CF=10$ ， $DE=5$ ，因为 $\tan \angle 1=\frac{2}{5}$ ，所以 $EB=DE\times tan\angle 1=2$ ，因为 $\angle 1=\angle 2$ (由第(1)问可得)，所以 $\tan \angle 2=\frac{2}{5}$ ，所以 $AE=\frac{DE}{\tan \angle 2}=\frac{25}{2}$ ， $AB=AE+EB=\frac{25}{2}+2=\frac{29}{2}$ ，所以 $OA=OB=\frac{29}{4}$ ，所以 $\odot O$ 的半径为 $\frac{29}{4}$ 。

Figure 14. Construct a right triangle diagonal midline theorem model

图14. 构造直角三角形斜边中线定理模型

【小结】本题解题的关键是构造直角三角形斜边中线定理模型，利用垂径定理的逆定理、对称的性质以及直角三角形斜边中线定理知识来解答。

4. 结束语

著名数学家、哲学家怀特海曾提出“数学是模式的科学”的观点，提出“数学的本质特征就是在模式化的个体抽象的过程中对模式进行研究” [4] 。这些题看似与中点模型无关，因为中点模型在题目中呈现不完整，其实通过构造中点模型便可迎刃而解。这需要学生在解题时深入思考、善于联想，充分挖掘题目隐含条件 [5] ，通过中点这一重要条件，构造符合题意的中点模型来解题，便可使推理过程柳暗花明。中考几何压轴试题难在知识综合与图形分解，这就需要教师在讲解典型例题时讲明问题的本质，讲清基本图形，引导学生理解其中蕴含的数学思想方法，掌握一般的解题策略，再次遇到类似问题时才能引发关联思考并解决问题 [6] 。并且在平时教学中，教师应该有意识地指导学生从问题中提炼一些解题模型，归纳一些常用方法，即引导学生进行有效的总结与反思，这既能加深学生对知识的理解，丰富学生的知识结构，又能提升学生分析问题与解决问题的能力，有助于学生综合能力的提升与数学素养的发展。

总之，在初中数学中包含有众多的数学模型，上述所呈现的中点模型只是其中的一类，在教学时需要使学生深刻领悟其中的内涵，掌握模型适用的范围及对应思路，逐步提升学生使用模型解题的灵活性，促进学生的思维发展 [7] 。

基金项目

国家自然科学基金资助(11961068)。

参考文献

NOTES

^*第一作者。

^#通讯作者。