卷积型Volterra积分微分方程的一种快速算法

A Fast Algorithm for Convolutional Volterra Integral Differential Equations

摘要: 卷积型Volterra积分微分方程是一类重要问题，广泛应用于生物学、经济学，本文研究了一种快速算法求解卷积型Volterra积分微分方程。该方法采用多步配置方法对卷积型Volterra积分微分方程进行离散，结合卷积核的特性，得到离散方程的线性系统由Toeplitz矩阵、对角矩阵和稀疏矩阵组合而成。考虑Toeplitz矩阵与向量的快速算法，设计系数矩阵与向量的快速计算格式。本文利用GMRES算法与快速计算格式结合，获得一种快速求解线性系统的改进算法，并通过实验验证改进算法的高效性。

Abstract: Convolutional Volterra integral differential equations are an important class of problems, widely used in biology, economics, among other fields. This study presents a fast algorithm for solving convolutional Volterra integral differential equations. The method involves discretizing the equations using a multi-step collocation approach, combined with the characteristics of the convolution kernels, resulting in a linear system of equations composed of Toeplitz matrices, diagonal matrices, and sparse matrices. Considering fast algorithms for Toeplitz matrices and vectors, a fast computation format for the coefficient matrix and vector is designed. By combining the GMRES algorithm with the fast computation format, an improved algorithm for efficiently solving linear systems is obtained. Experimental results verify the effectiveness of the improved algorithm.

1. 引言

研究卷积型Volterra积分微分方程(下面简称为卷积型VIDE)的快速算法，其方程形式如下

$\{\begin{array}{l}{y}^{\prime }\left(t\right)=a\left(t\right)y\left(t\right)+g\left(t\right)+{\displaystyle {\int }_0^{t}K\left(t-s\right)y\left(s\right)\text{d}s},t\in I:=\left[0,T\right],\hfill \\ y\left(0\right)=y_0,\hfill \end{array}$ (1)

其中 $a(\cdot ),g(\cdot )\in C\left(I\right)$ ， $K\left(t-s\right)$ 是区域 $D:=\left\{\left(t,s\right)|0\le s\le t\le T\right\}$ 上的连续函数，这些条件保证了式(1)解的存在唯一性 [1] 。

由于卷积型VIDE在生物学、经济学中有着广泛的应用，如计算生物学 [2] 、风险管理 [3] 等，因此对卷积型VIDE解的研究受到大量学者的关注。通常情况下，方程(1)的解析解很难求出，因此研究该方程的数值解法具有重要意义。迄今为止，国内外研究者提出和改进了很多有效求解VIDE数值解的方法，如差分求积法 [4] 、龙格–库塔法 [5] 、可约求积规则 [6] 、一般线性法 [7] [8] 、伽辽金法 [9] [10] 、配置方法 [1] 等。在文献 [10] 中的配置方法是显式类型的求解格式，可以逐步求解得到整个 $y\left(t\right)$ 在I上的数值逼近。 [11] 中的数值稳定性分析表示一些特殊的配置节点选取，可以导出 $A_0$ 稳定方法。此外，VDIE稳定数值解的另一种方法是使用超隐式技术 [12] 。通过使用下一个子区间的配置节点和Hermite-Birkhoff插值来研究求解非判别和刚性VIDE的多步配置方法。研究发现，使用计算的配置点明显扩大了稳定域。

在本文中，我们使用广义多步配置方法求解卷积型VIDE，广义多步配置方法通过在大区间上划分均匀网格，使用子区间两侧的网格节点构造局部多项式，类似的方法已经广泛用于Volterra积分方程中 [13] [14] [15] [16] ，这种方法具有简洁的形式，在不改变线性系统维度的情况下能够取得较高收敛阶的数值解。根据离散时产生线性系统的结构研究他的快速算法。在第2节中，构造求解卷积型VIDE的广义多步配置方法，分析求解卷积型VIDE的广义多步配置方法产生线性系统的结构，并结合GMRES [17] 算法得到快速求解算法。在第3节中，我们使用数值算例验证数值方法的高效性。

2. 快速广义多步配置方法

考虑使用广义多步配置方法 ${\text{GMCM}}^{k_1,k_2}$ 离散Volterra积分微分方程。设均匀网格 $I_h=\left\{t_n=nh|n=0,1,\cdots ,N\right\}$ ，其中步长 $h=T/N$ 。基于 $I_h$，定义局部基函数

${\varnothing }_j^{{\alpha }_n,{\beta }_n}\left(s\right)=\underset{i=-{\alpha }_n,i\ne j}{\overset{{\beta }_n+1}{{\displaystyle \prod }}}\frac{s-j}{j-i},j=-{\alpha }_n,\cdots ,{\beta }_n+1.$ (2)

进而导数在 $\left[t_n,t_{n+1}\right]$ 上的导数 $y^{\prime }\left(t\right)$ 具有如下表示

${Y^{\prime }}_h\left(t_n+sh\right)=\underset{i=-{\alpha }_n}{\overset{{\beta }_n+1}{{\displaystyle \sum }}}{Y^{\prime }}_{n+j}{\varnothing }_j^{{\alpha }_n,{\beta }_n}\left(s\right),s\in \left[0,1\right],$ (3)

其中 ${Y^{\prime }}_{n+i}:={Y^{\prime }}_h\left(t_n+jh\right)$ ，

$\left({\alpha }_n,{\beta }_n\right)=\{\begin{array}{l}\left(n,k_1+k_2-n\right),0\le n\le k_1-1,\\ \left(k_1,k_2\right),k_1\le n\le N-k_2-1,\\ \left(k_1+k_2+n+1-N,N-n-1\right),N-k_2\le n\le N-1,\end{array}$

$k_1,k_2$ 是非负整数。

在 $\left[t_n,t_{n+1}\right]$ 上对(3)积分

$Y_h\left(t_n+sh\right)=Y_n+h{\displaystyle \underset{i=-{\alpha }_n}{\overset{{\beta }_n+1}{\sum }}{Y^{\prime }}_{n+j}MO{M}_{n,j}}\left(s\right),s\in \left[0,1\right],$ (4)

其中 $Y_n:=Y_h\left(t_n\right)$ ， $MO{M}_{n,j}\left(s\right)={\displaystyle {\int }_0^s{\varnothing }_j^{{\alpha }_n,{\beta }_n}\left(v\right)\text{d}v}$ 。为了描述方程，定义下列符号 $MOMK{1}_{n,j}={\displaystyle {\int }_0^{1}K\left(t_{n+1}-t_j-sh\right)\text{d}s}$ ， $MOMK{2}_{n,j}^i={\displaystyle {\int }_0^{1}K\left(t_{n+1}-t_j-sh\right)MO{M}_{j,i}\left(s\right)\text{d}s}$ 。

进而我们得到

$\begin{array}{c}{\displaystyle {\int }_0^{t_{n+1}}K}\left(t_{n+1}-s\right)Y_h\left(s\right)\text{d}s={\displaystyle \underset{j=0}{\overset{n}{\sum }}{\displaystyle {\int }_{t_j}^{t_{j+1}}K}}\left(t_{n+1}-s\right)Y_h\left(s\right)\text{d}s\\ =h{\displaystyle \underset{j=0}{\overset{n}{\sum }}{\displaystyle {\int }_0^{1}K}}\left(t_{n+1}-t_j-vh\right)Y_h\left(t_j+vh\right)\text{d}v\\ =h{\displaystyle \underset{j=0}{\overset{n}{\sum }}{\displaystyle {\int }_0^{1}K}}\left(t_{n+1}-t_j-vh\right)\left(Y_j+h{\displaystyle \underset{i=-{\alpha }_j}{\overset{{\beta }_j+1}{\sum }}{Y^{\prime }}_{j+i}MO{M}_{j,i}\left(v\right)}\right)\text{d}v\\ =h{\displaystyle \underset{j=0}{\overset{n}{\sum }}{Y}_{j}MOMK{1}_{n,j}}+h^2{\displaystyle \underset{j=0}{\overset{n}{\sum }}{\displaystyle \underset{i=-{\alpha }_j}{\overset{{\beta }_j+1}{\sum }}{Y^{\prime }}_{j+i}MOMK{2}_{n,j}^i}}.\end{array}$

注意到

${Y^{\prime }}_n=a\left(t_{n+1}\right)Y_{n+1}+g\left(t_{n+1}\right)+{\displaystyle {\int }_0^{t_{n+1}}K\left(t_{n+1}-s\right)Y_h\left(s\right)\text{d}s},n=0,1,\cdots ,N-1.$ (5)

因此，我们有，

$\hat{P}{Y}_D=\hat{G},$ (6)

其中

$\hat{P}=E_N-hAF-h^{2}BF-h^{2}C,$

$\hat{G}=G_N+Y_0\left(A+hB\right)1+h{Y^{\prime }}_0\left(A{F}_0+hB{F}_0+h{C}_0\right)+h{Y}_0{B}_0,$

$\hat{B}={\left({\hat{b}}_{i,j}\right)}_{N\times \left(N+1\right)},{\hat{b}}_{i,j}=\{\begin{array}{ll}MOMK{1}_{n,j}\hfill & i>j,\hfill \\ 0,\hfill & i\le j,\hfill \end{array}$

$\hat{C}={\left({\hat{c}}_{i,j}\right)}_{N\times \left(N+1\right)},{\hat{c}}_{i,j}=\underset{k=-k_1-k_2}{\overset{k_1+k_2+1}{{\displaystyle \sum }}}MOMK{3}_{i-1,j-k}^k,$

$\hat{F}={\left({\hat{f}}_{i,j}\right)}_{N\times \left(N+1\right)},{\hat{f}}_{i,j}=\underset{k=-k_1-k_2}{\overset{k_1+k_2+1}{{\displaystyle \sum }}}MOMK{4}_{i-1,j-k}^k,$

$MOMK{3}_{i-1,j-k}^k=\{\begin{array}{ll}MOMK{2}_{i-1,j-k}^k,\hfill & \left(0<j-k\le \min \left(i-1,N-1\right)\&\left({\alpha }_{j-k}\le k\le {\beta }_{j-k}\right)\right),\hfill \\ 0,\hfill & 其他,\hfill \end{array}$

$MOMK{1}_{i-1,j-k}^k=\{\begin{array}{ll}MO{M}_{j-k,k}\left(1\right),\hfill & \left(0<j-k\le \min \left(i-1,N-1\right)\&\left({\alpha }_{j-k}\le k\le {\beta }_{j-k}\right)\right),\hfill \\ 0,\hfill & 其他,\hfill \end{array}$

$B=\hat{B}\left(1:N,2:N+1\right),B_0=\hat{B}\left(1:N,1\right),$

$C=\hat{C}\left(1:N,2:N+1\right),C_0=\hat{C}\left(1:N,1\right),$

$F=\hat{F}\left(1:N,2:N+1\right),F_0=F\left(1:N,1\right),$

$Y_D=\left(\begin{array}{c}{Y^{\prime }}_1\\ {Y^{\prime }}_2\\ ⋮\\ {Y^{\prime }}_N\end{array}\right),G_N=\left(\begin{array}{c}g\left(t_1\right)\\ g\left(t_2\right)\\ ⋮\\ g\left(t_N\right)\end{array}\right),A_N=\left(\begin{array}{cccc}a\left(t_1\right)& & & \\ & a\left(t_1\right)& & \\ & & \ddots & \\ & & & a\left(t_1\right)\end{array}\right).$

$1$ 表示元素全是1的N行1列的列向量，上述矩阵描述中 $i=1,2,\cdots ,N$ ， $j=1,2,\cdots ,N+1$ 。注意到 $MOMK{1}_{n,j}=MOMK{1}_{n+1,j+1}$ ， $n=0,1,\cdots ,N-2$ ， $j=0,1,\cdots ,N-1$ 。

当 $n=k_1,k_1+1,\cdots ,N-k_2-2$ 时， $MO{M}_{n,j}\left(s\right)=MO{M}_{n-1,j}\left(s\right)$ ，进而 $MOMK{2}_{n,j}^i=MOMK{2}_{n+1,j+1}^i$，因此，式(6)可以写为如下形式，

$\left(E_N-\left(hA+h^{2}B\right)\left(F_T+F_S\right)-h^2\left(C_T+C_S\right)\right)Y_D=\hat{G},$ (7)

即 $\hat{P}=E_N-hAF-h^{2}BF-h^{2}C=E_N-\left(hA+h^{2}B\right)\left(F_T+F_S\right)-h^2\left(C_T+C_S\right)$ ，其中 $B$ 是Toeplitz矩阵，其第一行元素为 $B\left(1,1:N\right)$ ，第一列元素为 $B\left(1:N,1\right)$ ， $F_T+F_S=F$ ， $C_T+C_S=C$ ， $F_T$ 是Toeplitz矩阵，其第一行元素为 $F_1=\left(F\left(k_1+k_2+1,k_1+k_2+1:N\right),0_{1\times \left(k_1+k_2\right)}\right)$ ，第一列元素为 $F_2=\left(F\left(k_1+k_2+1:N,k_1+k_2+1\right);0_{\left(k_1+k_2\right)\times 1}\right)$ ， $F_S$ 是稀疏矩阵，其非零元素及位置为 $F_S\left(:,i\right)=F\left(:,i\right)-\left(0_{\left(i-1\right)\times 1};F_2\left(1:N-i+1\right)\right)$ ， $i=1,2,\cdots ,k_1+k_2$ ， $F_S\left(N-j+1,N-k_1-k_2-1:i\right)=F\left(N-j+1,N-k_1-k_2-1:i\right)-\left(F_2{\left(k_1+k_2+3-j:-1:1\right)}^{\text{T}},F_1\left(1:j-1\right)\right)$ ， $j=1,2,\cdots ,k_2$ 。 $C_T$ 是Toeplitz矩阵，其第一行元素为 $C_1=\left(C\left(k_1+k_2+1,k_1+k_2+1:N\right),0_{1\times \left(k_1+k_2\right)}\right)$ ，第一列元素为 $C_2=\left(C\left(k_1+k_2+1:N,k_1+k_2+1\right);0_{\left(k_1+k_2\right)\times 1}\right)$ ， $C_S$ 是稀疏矩阵，其非零元素及位置为 $C_S\left(:,i\right)=C\left(:,i\right)-\left(0_{\left(i-1\right)\times 1};C_2\left(1:N-i+1\right)\right)$ ， $i=1,2,\cdots ,k_1+k_2$ ， $C_S\left(N-j+1,N-k_1-k_2-1:i\right)=C\left(N-j+1,N-k_1-k_2-1:i\right)-\left(C_2{\left(k_1+k_2+3-j:-1:1\right)}^{\text{T}},C_1\left(1:j-1\right)\right)$ ， $j=1,2,\cdots ,k_2$ 。注：上述过程中矩阵元素的选择参考Matlab矩阵元素的选取。此外在表1中，我们给出式子(7)中组成系数矩阵 $\hat{P}$ 的各部分矩阵的情况。

Table 1. Detailed table of matrices for each part during coefficient matrix P ^ decomposition

表1. 系数矩阵 $\text{<mover accent="true"> P <mo> ^ </mo> </mover>}$ 分解时各部分矩阵详细表

其中，

$D_{num}=\{\begin{array}{ll}{k}_{2}N+\left(k_1+k_2+2\right)k_2,\hfill & k_1=0,\hfill \\ \left(k_1+k_2+1\right)N+\left(k_1+k_2+2\right)k_2,\hfill & k_1>0,\hfill \end{array}$

对于Toeplitz矩阵，仅需要存储第一行和第一列即可，因此其存储量为2N。

如果不考虑 $\hat{P}$ 的结构，那么我们可以选择直接求解(6)式，需要 $O\left(N^3\right)$ 的计算量，或者使用迭代算法广义极小残差(GMRES)求解(6)式，其计算量主要来自于 $\hat{P}$ 与向量的乘法运算，因此需要 $O\left(N^2\right)$ 的计算量。根据表1可知，系数矩阵 $\hat{P}$ 由Toeplitz矩阵，稀疏矩阵，以及对角矩阵组合而成，充分利用 $\hat{P}$ 的结构，优化 $\hat{P}$ 与向量相乘时的计算量。

首先考虑Toeplitz矩阵与向量的快速计算，即根据已有的Toeplitz矩阵构造循环矩阵，进而通过快速Fourier方法计算。由Toeplitz矩阵T构造 $\hat{T}$ ，

$T=\left(\begin{array}{ccccc}{t}_0& t_{-1}& t_{-2}& \cdots & t_{-n}\\ t_1& t_0& t_{-1}& \cdots & t_{-n+1}\\ t_2& t_1& t_0& \cdots & t_{-n+2}\\ ⋮& ⋮& ⋮& & ⋮\\ t_n& t_{n-1}& t_{n-2}& \cdots & t_0\end{array}\right),\hat{T}=\left(\begin{array}{ccccc}0& t_n& t_{n-1}& \cdots & t_1\\ t_{n-1}& 0& t_n& \cdots & t_2\\ t_{n-2}& t_{n-1}& 0& \cdots & t_3\\ ⋮& ⋮& ⋮& & ⋮\\ t_{-1}& t_{-2}& t_{-3}& \cdots & 0\end{array}\right)$

将T与向量b的乘法嵌入式(8)计算，

$\left(\begin{array}{cc}T& \hat{T}\\ \hat{T}& T\end{array}\right)\left(\begin{array}{c}b\\ 0\end{array}\right)=\left(\begin{array}{c}Tb\\ \ast \end{array}\right)$ (8)

其中， $\left(\begin{array}{cc}T& \hat{T}\\ \hat{T}& T\end{array}\right)$ 是循环矩阵，与向量 $\left(\begin{array}{c}b\\ 0\end{array}\right)$ 的乘法使用快速Fourier方法计算，计算量为 $O\left(N\log \left(N\right)\right)$ 。而稀疏矩阵与向量的乘法所需计算量为 $O\left(N\right)$ ，对角矩阵与向量的乘法也是 $O\left(N\right)$ 。进而 $\hat{P}$ 与任意向量H的乘法 $\bar{G}:=\hat{P}H$ 可分为公式(9)中的5个步骤计算：

$\begin{array}{ll}{\bar{G}}_F=F_{T}H+F_{S}H,\hfill & \left(\text{step-1}\right)\hfill \\ {\bar{G}}_A=A{\bar{G}}_F,\hfill & \left(\text{step-2}\right)\hfill \\ {\bar{G}}_B=B{\bar{G}}_F,\hfill & \left(\text{step-3}\right)\hfill \\ {\bar{G}}_C=C_{T}H+C_{S}H,\hfill & \left(\text{step-4}\right)\hfill \\ \bar{G}=H-h\left({\bar{G}}_A+h{\bar{G}}_B+h{\bar{G}}_C\right).\hfill & \left(\text{step-5}\right)\hfill \end{array}$ (9)

Table 2. Formula (9) Calculation amount for each step

表2. 公式(9)各步的计算量

如表2所示，我们给出了使用公式(9)计算 $\hat{P}H$ 的各步骤的计算量，其中计算量最大的是Toeplitz矩阵与向量的快速计算，为 $O\left(N\log \left(N\right)\right)$ ，其余矩阵与向量的乘积中，计算量均为 $O\left(N\right)$ ，因此使用公式(9)计算 $\hat{P}H$ 的计算量为 $O\left(N\log \left(N\right)\right)$ 。

进而我们考虑GMRES算法(如算法1所示)，该算法中计算量主要来源于矩阵 $\hat{P}$ 与向量的乘法即第2行 $\hat{P}{Y}_D^{\left(0\right)}$ 与第4行 $\hat{P}{v}^{\left(i\right)}$ 的计算，这个两步的计算量均为 $O\left(N^2\right)$ 。考虑矩阵 $\hat{P}$ 与向量的快速计算格式公式(9)，结合GMRES算法，我们得到算法2所示的改进算法，进而可以将第2行 $\hat{P}{Y}_D^{\left(0\right)}$ 与第4行 $\hat{P}{v}^{\left(i\right)}$ 的计算量降为 $O\left(N\log \left(N\right)\right)$ ，从而优化整个算法的计算量。

Algorithm 1. GMRES algorithm for solving linear systems $\text{<mover accent="true"> P <mo> ^ </mo> </mover>}{Y}_D=\text{<mover accent="true"> G <mo> ^ </mo> </mover>}$

算法1. GMRES算法求解线性系统 $\text{<mover accent="true"> P <mo> ^ </mo> </mover>}{Y}_D=\text{<mover accent="true"> G <mo> ^ </mo> </mover>}$

Algorithm 2. Improved algorithm for solving linear systems $\text{<mover accent="true"> P <mo> ^ </mo> </mover>}{Y}_D=\text{<mover accent="true"> G <mo> ^ </mo> </mover>}$

算法2. 改进算法求解线性系统 $\text{<mover accent="true"> P <mo> ^ </mo> </mover>}{Y}_D=\text{<mover accent="true"> G <mo> ^ </mo> </mover>}$

Algorithm 3. UPDATA $\left({\bar{Y}}_D,i\right)$ algorithm

算法3. UPDATA $\left({\bar{Y}}_D,i\right)$ 算法

3. 实例分析与应用

在本节中，我们通过数值算例说明改进算法求解线性系统(7)的高效性，实验主要对比GMRES求解线性系统(7)与改进算法求解线性系统(7)的CPU计算时间，收敛时的相对残差，迭代次数，迭代过程中的相对残差变化情况。

例：求解卷积型Volterra积分微分方程

$y^{\prime }\left(t\right)=\frac{2}{1+t}y\left(t\right)+{\text{e}}^t+{\displaystyle {\int }_0^{t}2\cos }\left(t-s\right)y\left(s\right)\text{d}s,$

其中 $y\left(0\right)=1,t\in \left[0,8\right]$ ，其解析解是 $y={\left(1+t\right)}^2{\text{e}}^t$ 。数值实验是在Matlab2019a中实现的，其中，给定收敛条件为相对残 $\epsilon <{10}^{-10}$ ，

$\epsilon ={\Vert \hat{G}-\hat{P}{Y}_D\Vert }_2/{\Vert \hat{G}\Vert }_2.$

Table 3. GMCM 0 , 2 : Comparison of GMRES and improved algorithm solution time

表3. ${\text{GMCM}}^{0,2}$ ：GMRES与改进算法求解时长对比

Table 4. GMCM 1 , 1 : Comparison of GMRES and improved algorithm solution time

表4. ${\text{GMCM}}^{1,1}$ ：GMRES与改进算法求解时长对比

对区间 $\left[0,8\right]$ 作等距划分，取不同N，对于 ${\text{GMCM}}^{0,2},{\text{GMCM}}^{1,1},{\text{GMCM}}^{2,0}$ 得到的线性系统分别使用GMRES算法和改进算法求解所得CPU计算时长如表3，表4和表5，图1给出了迭代过程中相对残差的变化情况，图2给出了两种求解算法的CPU计算时间。

从表3、表4和表5中可知对于指定算法结束条件相对残 $\epsilon <{10}^{-10}$ ，GMRES算法和改进算法结束时相对残差几乎相同，且迭代次数相同，但随N增大，改进算法的CPU计算时间会小于GMRES算法的

Table 5. GMCM 2 , 0 : Comparison of GMRES and improved algorithm solution time

表5. ${\text{GMCM}}^{2,0}$ ：GMRES与改进算法求解时长对比

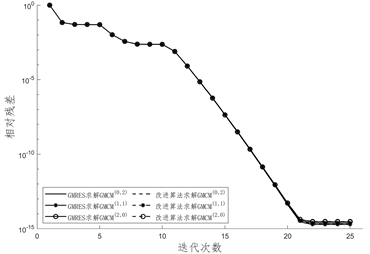
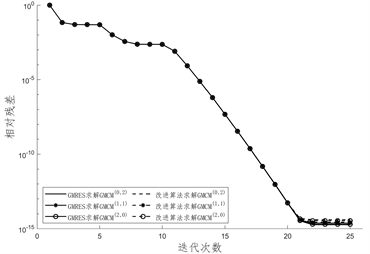(a) N = 100(b) N = 200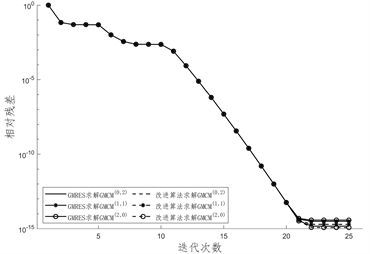 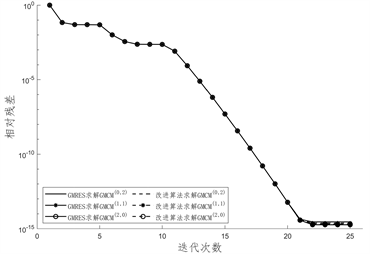(c) N = 400 (d) N = 800

Figure 1. Changes in relative residuals during the iteration process

图1. 迭代过程中相对残差变化情况

CPU计算时间，当N增大一倍，GMRES算法的计算时间增加倍数逐渐趋近于4，改进算法的CPU计算时间增长倍数逐渐趋近于2。

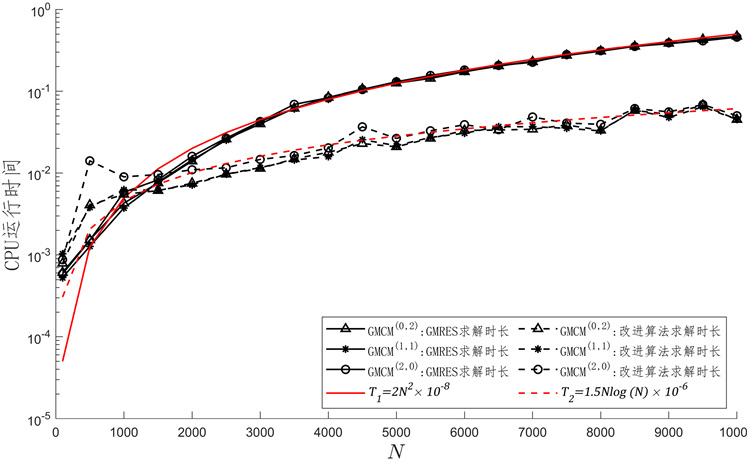
Figure 2. Comparison between GMRES and improved algorithms in solving problems

图2. GMRES 与改进算法求解时对比

图1给出迭代过程中相对残差的变化情况，针对本文所取的例子，不同方法获得的线性系统在求解过程中相对残差没有较大差距，且GMRES方法和改进算法的相对残差也没有较大差距。在图2中，我们绘制了GMRES算法与改进算法求解 ${\text{GMCM}}^{0,2},{\text{GMCM}}^{1,1},{\text{GMCM}}^{2,0}$ 的CPU计算时长，以及两条参考曲线 $T_1=2N^2\times {10}^{-8},T_2=1.5N\log N\times {10}^{-6}$ 。当N增大时，GMRES算法的求解时间靠近 $T_1$ ，改进算法的求解时间靠近 $T_2$ ，也就是说GMERS的算法求解时间为 $O\left(N^2\right)$ ，GMRES的求解时间为 $O\left(N\log \left(N\right)\right)$ ，验证了第1节GMRES算法的计算量为 $O\left(N^2\right)$ ，改进算法的计算量为 $O\left(N\log \left(N\right)\right)$ 。而且 $k_1,k_2$ 的值对GMRES和改进算法的CPU计算时间影响不大，两种求解线性系统的算法与线性系统的维度 有关。此外，从图中可知随着N变大，改进算法的计算时间小于GMRES的计算时间且改进算法的CPU计算时间的增长率小于GMRES，因此改进算法能够快速高效计算卷积型VIDE离散出的大型线性系统。

4. 结论

使用广义多步配置方法( ${\text{GMCM}}^{k_1,k_2}$ )离散卷积型VIDE，分析离散后的线性系统的结构组成，结合Toeplitz矩阵与向量的快速计算，进而得到系数矩阵与向量的快速计算。使用GMRES算法与快速计算格式结合，构建了一种适合求解该类线性系统的改进算法，改进后的算法的计算量只需 $O\left(N\log \left(N\right)\right)$ ，比GMRES算法的计算量更小，从实验结果看，改进算法与GMRES算法在求解同一问题时，改进算法需要的求解时间比GMRES算法的求解时间更短，当N值增大时，改进算法在计算时间上更小，更具优势。因此改进算法可以高效求解这一类大规模线性系统。