捕食者攻击速率对具有额外捕食的常微分方程–反应扩散方程耦合模型影响研究

The Effect of Predator Attack Rate on the Coupled Model of Ordinary Differential Equation and Reaction-Diffusion Equation with Additional Predation

摘要: 本文研究了捕食者攻击速率对一类具有额外捕食的常微分方程–反应扩散方程耦合模型的影响。我们发现捕食者攻击速率不仅会影响到Allee效应的类型，也会影响到物种存活以及共存模式，还会影响到斑图的产生及其类型。

Abstract: In this paper, the effect of predator attack rate on a class of coupled ordinary differential equation and reaction-diffusion equation models with additional predation is studied. We found that the predator attack rate not only affects the type of Allee effect, but also affects the species survival and coexistence mode, and also affects the generation and type of pattern.

1. 引言

在自然界中，捕食者–食饵关系是随处可见的。例如，非洲野生草原上的狮子–斑马，亚马逊热带雨林中的蚺–貘，日本北海的虎鲸–乌贼，台湾北部天空中的凤头苍鹰–麻雀等都是经典的捕食者–食饵关系。近年来，许多生物数学学者对捕食食饵系统深入研究。其中，文章 [1] 研究了如下具有额外捕食的捕食食饵系统：

$\{\begin{array}{l}{u}^{\prime }=ru\left(1-\frac{u}{K}\right)-\frac{au}{1+mu}-\alpha uv\\ v^{\prime }=\beta uv-dv\end{array}$ (1)

其中， $u,v$ 分别代表食饵和捕食者的密度， $r,K,a,\alpha ,\beta ,d$ 都是正参数，分别代表食饵的内禀增长率、环境最大容纳量、捕食者的攻击速率、消耗率、转化率和死亡率。文章 [1] 研究该模型并将它分为如下的四个参数区域：强Allee区 ${\mathcal{D}}_1$ 、弱Allee区 ${\mathcal{D}}_2$ 、无Allee区 ${\mathcal{D}}_3$ 和灭绝区 ${\mathcal{D}}_0$ ：

${\mathcal{D}}_0=\left\{\left(a,r,m,K\right)\in R_{+}^4:\frac{a}{r}>1,\frac{1}{mK}>1\right\}\cup \left\{\frac{a}{r}>\frac{{\left(mK+1\right)}^2}{4mK}\right\}$ (2)

${\mathcal{D}}_1=\left\{\left(a,r,m,K\right)\in R_{+}^4:\frac{1}{mK}<1<\frac{a}{r}<\frac{{\left(mK+1\right)}^2}{4mK}\right\}$ (3)

${\mathcal{D}}_2=\left\{\left(a,r,m,K\right)\in R_{+}^4:armK>0,\frac{1}{mK}<\frac{a}{r}<1\right\}$ (4)

${\mathcal{D}}_3=\left\{\left(a,r,m,K\right)\in R_{+}^4:\frac{a}{r}<1,\frac{a}{r}<\frac{1}{mK}\right\}$ (5)

然而，上面描述的ODE模型只反映了种群随时间的演化，但在现实世界中，除了时间还有另外一种绝对不能忽视的因素——空间。物种会在其生存环境中不断的扩散，从而可能会改变只有时间因素的模型对于稳定性方面的研究结果。近年来有许多国内外学者对此做出了研究，如 [2] [3] [4] [5] 。此外，文章 [6] 在 [1] 所研究的ODE模型(1)的基础上引入了空间扩散项，提出了如下的交叉扩散模型，并研究了在弱Allee条件下的图灵失稳等问题。

$\{\begin{array}{ll}\frac{\partial u}{\partial t}=d_{11}\Delta u+d_{12}\Delta v+ru\left(1-\frac{u}{K}\right)-\frac{au}{1+mu}-\alpha uv\hfill & x\in \Omega ,t>0\hfill \\ \frac{\partial v}{\partial t}=d_{21}\Delta u+d_{22}\Delta v+\beta uv-dv\hfill & x\in \Omega ,t>0\hfill \\ \frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0\hfill & x\in \partial \Omega \hfill \\ u\left(x,0\right)=u_0\left(x\right)\ge 0,v\left(x,0\right)=v_0\left(x\right)\ge 0\hfill & x\in \Omega \hfill \end{array}$ (6)

这里， $\Omega =\left[0,L\right]\times \left[0,L\right]$ ； $\Delta =\frac{{\partial }^2}{\partial x^2}+\frac{{\partial }^2}{\partial y^2}$ 是拉普拉斯算子； $\frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0$ 指Neuman边界条件，代表着物种不会跑出这个边界； $u\left(x,0\right)=u_0\left(x\right)\ge 0,v\left(x,0\right)=v_0\left(x\right)\ge 0$ 则代表着物种正的初值，符合现实意义。

本文中，我们重点研究捕食者对食饵的攻击速率对 [1] 的ODE模型(1)和 [6] 的PDE模型(6)的影响。在第二节，我们通过对模型(1)的四个参数区域(2)~(5)进行改写，以体现捕食者攻击速率对Allee效应的影响。在第三节中，我们通过改变攻击速率并用数值模拟体现ODE模型相平面图变化过程，以探寻对于稳态的影响。在第四节，我们通过对PDE模型(6)的进行数值模拟，并探讨捕食者攻击速率对图灵失稳和斑图类型的影响。最后，我们把我们得到的结论进行总结。

2. 捕食者攻击速率对Allee效应的影响

为了突出捕食者攻击速率a对Allee效应的影响，我们先将分区参数条件(2)~(5)进行修改调整。定义如下：

$a_1=\frac{r{\left(mK+1\right)}^2}{4mK},a_2=r,a_3=\frac{r}{mK}$ (7)

在一个环境容纳量K较大 $\left(K>\frac{1}{m}\right)$ 的环境中，很容易知道， $a_3<a_2<a_1$ 。则灭亡区、强Allee区、弱Allee区、无Allee区分别对应 $a>a_1,a_2<a<a_1,a_3<a<a_2,0<a<a_3$ 。

而在一个环境容纳量K较小 $\left(K<\frac{1}{m}\right)$ 的环境中，只可能出现灭亡区和无Allee区，分别对应 $a>a_2,a<a_2$ 。

上述结果告诉我们，在其他参数固定的情况下，我们有如下结论：

结论1：

1) 高环境容纳量 $\left(K>\frac{1}{m}\right)$ 下，捕食者的攻击速率a很大时 $\left(a\in \left(a_1,+\infty \right)\right)$ ，会导致灭亡区的出现；当捕食者的攻击速率a逐渐降低，会依次经历强Allee区 $\left(a\in \left(a_2,a_1\right)\right)$ 、弱Allee区 $\left(a\in \left(a_3,a_2\right)\right)$ 、无Allee区 $\left(a\in \left(0,a_3\right)\right)$ 。

2) 低环境容纳量 $\left(K<\frac{1}{m}\right)$ 下，强Allee区和弱Allee区消失，当捕食者的攻击速率a较大时 $\left(a>a_2\right)$ ，会进入灭亡区；较小 $\left(a<a_2\right)$ 则会进入无Allee区。

例如，当我们让 $r=1,m=1$ 时，可以得到如下的图1，这是结论1的直观反映。

3. 捕食者攻击速率对ODE模型物种存活的影响

现在，为了方便研究平衡点稳定性，我们先定义如下的非线性函数

$H\left(u\right)=r\left(1-\frac{u}{K}\right)-\frac{a}{1+mu}=\frac{h\left(u\right)}{K\left(1+mu\right)}$ (8)

这里，

$h\left(u\right)=-rm{u}^2+r\left(mK-1\right)u+\left(r-a\right)K$ (9)

则 $h\left(u\right)$ 的根为：

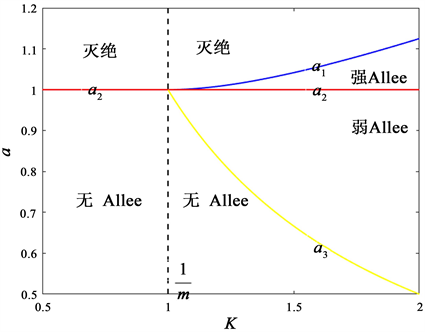
Figure 1. Allee zoning diagram of predation rate under different environmental capacities

图1. 不同环境容纳量下捕食速率Allee分区图

${\theta }_i=\frac{r\left(mK-1\right)\pm \sqrt{{\left[r\left(mK-1\right)\right]}^2-4rmK\left(a-r\right)}}{2rm},i=1,2$ (10)

因此，我们可以将方程(1)简写成：

$\{\begin{array}{l}{u}^{\prime }=uH\left(u\right)-\alpha uv\\ v^{\prime }=\beta uv-dv\end{array}$ (11)

结合(8)~(12)，由 [1] 对模型(11)平衡点的分析，结合结论1，我们有：

引论2：

1) 高环境容纳量 $\left(K>\frac{1}{m}\right)$ 下：

(i) 当 $a\in \left(a_1,+\infty \right)$ ，模型(11)的平衡点只有 $\left(0,0\right)$ ，所有物种灭亡。

(ii) 当 $a\in \left(a_2,a_1\right)$ ，模型(11)有平衡点 $\left(0,0\right),\left({\theta }_1,0\right),\left({\theta }_2,0\right)$ ，并且当 $\frac{d}{\beta }\in \left({\theta }_1,{\theta }_2\right)$ 有内平衡点 $E^{\ast }\left(\frac{d}{\beta },\frac{H\left(\frac{d}{\beta }\right)}{\alpha }\right)$ 。

(iii) 当 $a\in \left(0,a_2\right)=\left(0,a_3\right)\cup \left(a_3,a_2\right)$ ，模型(11)有平衡点 $\left(0,0\right),\left({\theta }_2,0\right)$ ，并且当 $\frac{d}{\beta }\in \left(0,{\theta }_2\right)$ 有内平衡点 $E^{\ast }\left(\frac{d}{\beta },\frac{H\left(\frac{d}{\beta }\right)}{\alpha }\right)$ 。

2) 低环境容纳量 $\left(K<\frac{1}{m}\right)$ 下：

(i) 当 $a\in \left(a_2,+\infty \right)$ ，模型(11)的平衡点只有 $\left(0,0\right)$ ，所有物种灭亡。

(ii) 当 $a\in \left(0,a_2\right)$ ，模型(11)有平衡点 $\left(0,0\right),\left({\theta }_2,0\right)$ ，并且当 $\frac{d}{\beta }\in \left(0,{\theta }_2\right)$ 有内平衡点 $E^{\ast }\left(\frac{d}{\beta },\frac{H\left(\frac{d}{\beta }\right)}{\alpha }\right)$ 。

例如，我们取 $r=1,m=1,\alpha =1,\beta =1,d=0.2$ ，容易得到 $a_3=0.5,a_2=1,a_1=1.125$ ，在高环境容纳量 $K=2>\frac{1}{m}$ 的情况下，分别取 $a=0.4,0.6,0.8,1.05,1.1,2$ ，我们分别得到图2的(a)~(f)六个子图；在低环境容纳量 $K=0.5<\frac{1}{m}$ 的情况下，分别取 $a=0.6,0.8,1.5$ ，我们分别得到图2的(g)~(i)三个子图。

在高环境容纳量下，当 $a=0.4\in \left(0,a_3\right)$ ，模型(11)展现无Allee效应(如图2(a))，可见此时捕食者和食饵都可以在内平衡点处共存；当 $a=0.6,0.8\in \left(a_3,a_2\right)$ ，模型(11)展现弱Allee效应(如图2(b)、图2(c))，可见随着捕食者攻击速率的增大，捕食者和食饵都可以共存，但共存方式由稳态转变为振荡态(出现极限环)；当 $a=1.05,1.1\in \left(a_2,a_1\right)$ ，模型(11)展现强Allee效应(如图2(d)、图2(e))，可以看到，随着捕食者攻击速率的增大，捕食者和食饵慢慢不共存了，由共存态正转变为灭绝态；当 $a=2\in \left(a_1,+\infty \right)$ ，处于灭亡区(见图2(f))，可以看到两个边界平衡点也消失了，捕食者和食饵将会灭绝。

(a) $K=2,a=0.4$ (b) $K=2,a=0.6$ (c) $K=2,a=0.8$ (d) $K=2,a=1.05$ (e) $K=2,a=1.1$ (f) $K=2,a=2$ (g) $K=0.5,a=0.6$ (h) $K=0.5,a=0.8$(i) $K=0.5,a=1.5$

Figure 2. The phase plane of model (12) with a changes

图2. 随a变化下模型(12)的相平面

在低环境容纳量下，当 $a=0.6,0.8\in \left(0,a_2\right)$ ，模型(12)展现无Allee效应(如图2(g)、图2(h))，可见随着捕食者攻击速率的增大，从“捕食者食饵共存”变为“仅有食饵共存”；当 $a=1.5\in \left(a_2,+\infty \right)$ ，模型(12)处于灭亡区(如图2(i))，可见当捕食者的攻击速率太大时，捕食者和食饵将会一起灭绝。

总而言之，我们有以下结论：

结论2：

随着捕食者攻击速率的增加，捕食者和食饵会从共存态转变为灭绝态。在这之中，可能伴随着共存态从稳态转变为极限环振荡态，而灭绝态从捕食者单灭绝转变为捕食者食饵双灭绝的演变情形。

4. 捕食者攻击速率对PDE模型图灵斑图的影响

为了研究捕食者攻击速率对PDE模型(6)的图灵斑图存在性及其类型的影响，为此，据 [6] 的数值模拟方法，我们对模型(6)进行数值模拟。通过如下的五点差分格式

$\Delta u_{ij}^k=\frac{{\partial }^{2}u}{\partial x^2}+\frac{{\partial }^{2}u}{\partial y^2}=\frac{u_{i,j+1}^k+u_{i,j-1}^k+u_{i+1,j}^k+u_{i-1,j}^k-4u_{ij}^k}{h^2}$ (19)

可以实现对拉普拉斯算子做离散化，这里h指的是空间步长。再者，通过设置在正平衡点 $E^{\ast }$ 附近的随机小扰动作为初值。我们用Matlab进行数值模拟，并将网格固定为50 × 50，空间步长为1，时间步长为0.01，演变时间为50,000。固定 $r=1,m=1,\alpha =1,\beta =1,d=0.2,K=2,d_{11}=3,d_{12}=1,d_{21}=6,d_{22}=3$ ，取 $a=0.05,0.08,1.02,1,1.1$ ，我们观察到如下的斑图变化。

(a) $a=0.05$ (b) $a=0.0\text{8}$(c) $a=1$ (d) $a=1.02$(e) $a=1.1$

Figure 3. The Turing pattern model (6) with a changes

图3. 随a变化下模型(6)的斑图情况

由图3(a)~(e)，我们知道当捕食者攻击速率太低时，模型(6)呈现稳态，没有图灵斑图出现。而随着捕食者攻击速率增加，会使得模型(6)从稳态变为图灵失稳，并且可以展现出不同的斑图类型(点斑图→混合斑图→线斑图)。当捕食者攻击速率很大时，食饵会灭亡，自然也没有图灵斑图出现。因此，我们有如下结论：

结论3：

适中的捕食者攻击速率有利于图灵斑图的产生。

5. 总结

本文研究了捕食者攻击速率对一类具有额外捕食的常微分方程–反应扩散方程耦合模型捕食食饵系统的影响。我们发现，通过选择不同的捕食者攻击速率参数，会改变Allee效应，通常捕食者攻击速率的增大会促使从无Allee区到弱Allee区到强Allee区再到灭绝区。此外，我们发现捕食者攻击速率还会影响到物种的生存灭亡以及共存模式，通常捕食者攻击速率的增大会使得模型从共存态变为灭绝态，在这其中可能还伴随着共存模式的改变以及灭绝类型的改变。最后，捕食者攻击速率还会影响到图灵斑图的产生以及斑图类型，适中的捕食者攻击速率有利于产生图灵斑图。

本文叙述的问题是在文献 [1] [6] 的基础上进行研究的， [1] [6] 没有关注到捕食者攻击速率的具体影响。本文对 [1] [6] 的研究结果进行了扩展与补充，得到了一些有意义的生物现象，这对于生态防控具有一定的指导意义。