局部线性回归的核函数分析

Kernel Function Analysis for Local Linear Regression

摘要: 非参数回归方法有很多，最常用的是局部多项式回归，局部线性回归是局部多项式回归的特例，局部线性回归较好的克服了边界的偏差，且有良好的渐近性质和收敛速度，因此运用较为广泛。本文采用局部线性回归方法，研究不同核函数和样本量对积分均方偏差、积分方差和积分均方误差的影响，首先研究在不同核函数下，绘制用局部线性回归方法得到的拟合值和真实值的图像，然后研究在不同核函数和样本量下，使用局部线性回归方法对积分均方偏差、积分方差和积分均方误差的影响。

Abstract: There are many nonparametric regression methods, the most commonly used is local polynomial regression, local linear regression is a special case of local polynomial regression. Local linear re-gression better overcomes the bias of the boundaries, and has good asymptotic properties and convergence speed, so it is more widely used. In this paper, we use the local linear regression method to study the effect of different kernel functions and sample sizes on the integral mean-square deviation, integral variance and integral mean-square error. Firstly, we study to plot the images of the fitted values and the true values obtained by using the local linear regression method with different kernel functions. Then we study to study the effect of the use of the local linear regression method on the integral mean-square deviation, integral variance and integral mean-square error with different kernel functions and sample sizes.

1. 引言

在双变量情况下，探索协变量与响应变量之间的关联是共同感兴趣的课题，描述这种关联的一种可能方法是通过均值回归函数。回归方法可以分为参数方法和非参数方法两种，其中参数方法需要明确函数服从具体的分布、确定模型的形式并给出参数估计值，采用参数回归方法，可以得到外延性较好的回归结果，并且具有较高的估计精度。但参数方法存在一个缺点：一旦函数形式确定，就会显得相对固定，从而拟合效果可能不尽如人意。与之相比，非参数方法则无需加入任何先验知识，它们是基于数据本身的特点和性质来拟合分布的。此外，非参数方法不限制解释变量的分布状况和模型的具体形式，因此适用于各种密度形状的拟合。这使得非参数方法具有更大的灵活性和适用性。非参数方法相比参数方法更稳健，但非参数方法容易受到维数问题的困扰。在统计学中，灵活的估计方法要求不对该函数的形式做任何假设。这种形式应该完全由数据决定。换句话说，非参数方法比参数方法更有优势、更可取。在实际问题中，应根据具体问题选择合适的方法，并考虑其优劣，以获得更准确、可靠的估计结果。

$Y=m\left(x\right)+\epsilon$

其中 $m\left(x\right)$ 是未知待估计的光滑函数， $\epsilon$ 是随机误差项，其中 $\epsilon$ 具有零均值，有限方差的独立同分布随机变量。为了处理未知待估计的非参数光滑函数 $m\left(x\right)$ ，目前存在多种有效的方法可供选择。这些方法包括光滑样条法、正交回归、核回归、局部多项式回归、近邻回归、稳健回归、多元局部回归和薄板样条等。其中，局部多项式回归及其稳健形式是广泛认为的高效非参数光滑估计方法。局部线性回归可看作是局部多项式回归的一个特例，在国内外都受到广泛研究和应用。使用这些方法可以更好地处理未知待估计的非参数光滑函数，从而提高各领域的建模和预测准确性。在局部线性回归中，核函数的选择对于模型的拟合效果至关重要。常见的核函数包括高斯核、Epanechnikov核和三角核等。不同的核函数有不同的平滑程度和边缘效应，因此在选择核函数时需要根据具体问题进行选择。同时，核函数的带宽大小也会影响模型的拟合效果。因此，在进行局部线性回归时，应根据具体问题选择合适的核函数和带宽大小，并使用交叉验证等技术来评估模型的拟合效果，以获得更准确、可靠的估计结果。本文研究的重点是局部线性回归中核函数的选择问题，并探讨不同核函数对局部线性回归模型拟合效果的影响。

Fan和Gijbels (1992) [1] 采用局部线性回归方法估计均值回归函数，并提供了估计函数的均方误差和均方积分误差。Cleveland (1979) [2] 研究了稳健拟合过程以防止偏差点偏离平滑点，并探讨了稳健局部加权回归的计算和统计问题，为数据建模和预测提供了实用方法。Fan (1992b) [3] 阐明了局部线性回归的平滑性和其优势，为该方法的发展提供了理论支持。Hamilton (1997) [4] 则讨论了在偏回归方法中使用局部线性回归方法估计回归函数，并给出了估计值的渐近分布。He和Huang (2009) [5] 构建了一个二次光滑局部线性回归估计量，通过将x邻域中局部线上的所有拟合点与其另一个平滑点组合起来，通过积分来构造二次光滑局部线性回归估计量，该估计量与局部线性回归估计量相当。Hengartner (2002) [6] 提出了一种将非参数回归估计量带宽选择方法应用于局部线性回归中的方式，该方法具有良好的有限样本性能。Jones (1990) [7] 从涉及的思想和理论角度区分核密度估计是使用相同带宽还是不同带宽。Ruppert (1995) [8] 应用插入带宽选择的思想研究局部线性平方核估计的平滑参数选择，其结果表明该方法适用于奇数阶局部多项式拟合。这些方法和技术在数据建模和预测中具有广泛的应用，对实践工作者具有重要的指导意义。

本文的结构安排如下：第一章主要介绍选题的意义，背景和研究现状。第二章主要介绍局部线性回归的概念以及局部线性回归的估计。第三章主要介绍局部线性回归的一些结论，局部线性回归的渐近偏差和渐近方差以及核函数选择的分析。第四章主要进行数值模拟。第五章主要提出一些结论性意见。

2. 局部线性回归

独立随机样本 $\left(X_1,Y_1\right),\left(X_2,Y_2\right),\cdots ,\left(X_n,Y_n\right)$ 来自模型 $Y=m\left(X\right)+\sigma \left(X\right)\epsilon$ ，其中X与 $\epsilon$ 相互独立， $E\left(\epsilon \right)=0$ ， $Var\left(\epsilon \right)=1$ ，对于任意给定的下，其附近的点 $X_i$ 的函数值可有泰勒展开逼近，即：

$m\left(X_i\right)\approx m\left(x\right)+m^{\prime }\left(X_i-x\right)+\cdots +m^{\left(p\right)}{\left(X_i-x\right)}^{\left(p\right)}/p!$

取 $p=1$ ， $K(\cdot )$ 是对称的核密度函数，即 $K\ge 0$ ， ${\displaystyle \int K}=1$ 并且 $K\left(-x\right)=K\left(x\right)$ ，由加权最小二乘法，使

${\displaystyle \underset{i=1}{\overset{n}{\sum }}{\left\{Y_i-\left({\beta }_0+{\beta }_1\left(X_i-x\right)\right)\right\}}^2{K}_h\left(X_i-x\right)}$ (2.1)

达到最小，其中 $K_h\left(u\right)=K\left(u/h\right)/h$ ，h是个光滑参数，它控制预测点x领域的长度，称作带宽，那么得到局部线性回归估计 $\hat{m}\left(x\right)={\hat{\beta }}_0\left(x\right)$ ，通过加权最小二乘方法使得(2.1)式达到最小，令

$X=\left(\begin{array}{cc}1& X_1-x\\ ⋮& ⋮\\ 1& X_n-x\end{array}\right)$ , $Y=\left(\begin{array}{c}{Y}_1\\ ⋮\\ Y_n\end{array}\right)$ , $\hat{\beta }=\left(\begin{array}{c}{\hat{\beta }}_0\\ {\hat{\beta }}_1\end{array}\right)$

并且 $W\left(x\right)$ 表示 $n\times n$ 的对角矩阵，具体表示为

$W\left(x\right)=diag\left[K_h\left(X_1-x\right),\cdots ,K_h\left(X_n-x\right)\right]$

则(2.1)式的加权最小二乘问题可以转化为

$\underset{\beta }{\min }{\left(Y-X\beta \right)}^{\text{T}}W\left(Y-X\beta \right)$ (2.2)

其中 $\beta ={\left({\beta }_0,{\beta }_1\right)}^{\text{T}}$ ，由加权最小二乘理论可以算出

$\hat{\beta }={\left(X^{\text{T}}WX\right)}^{-1}{X}^{\text{T}}WY$ (2.3)

为了得到更详细的计算结果，记

$s_{n,j}\left(x\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{K}_h}\left(X_i-x\right){\left(X_i-x\right)}^j$

$S_i\left(x\right)=\left\{s_{n,2}\left(x\right)-s_{n,1}\left(x\right)\left(X_i-x\right)\right\}{K}_h\left(X_i-x\right)/\left\{s_{n,0}\left(x\right)s_{n,2}\left(x\right)-s_{n,1}^2\left(x\right)\right\}$

$T_i\left(x\right)=\left\{-s_{n,1}\left(x\right)+s_{n,0}\left(x\right)\left(X_i-x\right)\right\}{K}_h\left(X_i-x\right)/\left\{s_{n,0}\left(x\right)s_{n,2}\left(x\right)-s_{n,1}^2\left(x\right)\right\}$

得到局部线性回归估计为

${\hat{\beta }}_0\left(x\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{S}_i}\left(x\right)Y_i,{\hat{\beta }}_1\left(x\right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{T}_i}\left(x\right)Y_i$ (2.4)

如果核密度函数 $K(\cdot )$ 的定义域为 $\left[-1,1\right]$ ，核密度函数自变量的观测点只有落在 $\left[x-h,x+h\right]$ 中观测点才能被用来估计 $\hat{m}\left(x\right)$ 。带宽h是决定预测点x邻域的大小的光滑参数。假设密度 $f\left(x\right)$ 的范围为 $\left[-2,2\right]$ ，核密度函数 $K(\cdot )$ 的范围为 $\left[-1,1\right]$ ，对于某个观测点完全落在 $\left[x-h,x+h\right]$ 区间之内，该观测点称为内点。此时，内点的取值范围被限制在 $\left[x-h,x+h\right]$ 区间之中。如果某个观测点的取值未完全包含在 $\left[x-h,x+h\right]$ 区间之内，则该点被认为是边界点。左边界点指的是该点位于密度区间左侧，其形式为 $\left[-2,-2+h\right)$ ，并且可以表示为一段区间的右端点；而右边界点则指该点位于密度区间右侧，其形式为 $\left(2-h,2\right]$ ，并且可以表示为一段区间的左端点。

3. 主要结论

3.1. 渐近性质

本节主要介绍了局部线性回归方法的数学表达式及其应用。在该方法中，利用局部线性回归来获得估计的渐近偏差和渐近方差。当核密度函数 $K(\cdot )$ 的范围是一个紧致区间时，只有落在该区间 $\left[x-h,x+h\right]$ 的观测点才能被用来进行估计 $\hat{m}\left(x\right)$ 。为控制预测点邻域的长度，引入带宽h作为一个光滑参数。假设密度 $f\left(x\right)$ 的范围为 $\left[-2,2\right]$ ，核密度函数 $K(\cdot )$ 的范围为 $\left[-1,1\right]$ ，对于某个观测点完全落在 $\left[x-h,x+h\right]$ 区间之内，该观测点称为内点。此时，内点的取值范围被限制在 $\left[x-h,x+h\right]$ 区间之中。局部线性回归估计的渐近偏差和渐近方差的表达式如下 [1] ：

$bias\left[\hat{m}\left(x\right)|X_1,\cdots ,X_n\right]=h^2\frac{m^{″}\left(x\right)}{2}{\mu }_2+o_p(\; h\; 2\; )$

$Var\left[\hat{m}\left(x\right)|X_1,\cdots ,X_n\right]=\frac{1}{nh}\frac{v_0}{f\left(x\right)}{\sigma }^2\left(x\right)+o_p\left(\frac{1}{nh}\right)$ (3.1)

其中 ${\mu }_j={\displaystyle \int u^j}K\left(u\right)\text{d}u$ ， $v_j={\displaystyle \int u^j}{K}^2\left(u\right)\text{d}u$ ， $j=0,1,2,\cdots$

而当 $\left[x-h,x+h\right]$ 不完全包含在密度区间内时，这样的x称为边界点，对于边界点(3.1)式将不在正确。假设密度 $f\left(x\right)$ 的范围为 $\left[-2,2\right]$ ，核密度函数 $K(\cdot )$ 的范围为 $\left[-1,1\right]$ ，如果某个观测点的取值未完全包含在 $\left[x-ch,x+ch\right]$ 区间之内，则该点被认为是边界点。左边界点指的是该点位于密度区间左侧，其形式为 $\left[-2,-2+ch\right)$ ，并且可以表示为一段区间的右端点；而右边界点则指该点位于密度区间右侧，其形式为 $\left(2-ch,2\right]$ ，并且可以表示为一段区间的左端点。其中 $0\le c<1$ 。对于边界点，用局部线性回归的估计的渐近偏差和渐近方差为 [9] ：

$bias\left[\hat{m}\left(x\right)|X_1,\cdots ,X_n\right]=h^2\frac{m^{″}\left(x\right)}{2}{B}_0\left(c\right)+o_p(\; h\; 2\; )$

$Var\left[\hat{m}\left(x\right)|X_1,\cdots ,X_n\right]=\frac{1}{nh}\frac{V_0\left(c\right)}{f\left(x\right)}{\sigma }^2\left(x\right)+o_p\left(\frac{1}{nh}\right)$ (3.2)

其中 $B_0\left(c\right)=\left({\mu }_{2,c}^2-{\mu }_{1,c}{\mu }_{3,c}\right)/\left({\mu }_{0,c}{\mu }_{2,c}-{\mu }_{1,c}^2\right)$ ， ${\mu }_{j,c}={\displaystyle {\int }_{-c}^1{u}^{j}K\left(u\right)\text{d}u}$ ， $V_0\left(c\right)={\displaystyle {\int }_{-c}^1\left({\mu }_{2,c}-u{\mu }_{1,c}^2\right)K^2\left(u\right)\text{d}u/{\left({\mu }_{0,c}{\mu }_{2,c}-{\mu }_{1,c}^2\right)}^2}$ 。

3.2. 核函数和带宽选择

在进行函数估计时，选择合适的核函数和带宽是非常重要的。最初引入核函数是为了解决高维数据的计算难题。通过选择适当的函数，可以避免“维度灾难”，并显著减少计算量，从而提高估计函数的效率。在核密度估计中，带宽的大小尤为关键。如果带宽过大，会导致过度平滑，而如果带宽过小，则会出现欠平滑现象。带宽可分为常带宽和变带宽两种类型。常带宽适用于未知曲线摆动幅度较小、具有高平滑度的情况。然而，当未知曲线具有相当复杂的结构时，常带宽无法很好地工作。这就需要选择可变带宽，以更好地捕捉曲线的复杂性。与此同时，在核函数的选择上也需谨慎。例如，高斯核通常是最常用的核函数之一，但并不总是适用于所有情况。其他类型的核函数，如Epanechnikov核函数、Biweight核函数也可以被使用。因此，在实际应用中，应根据具体问题来确定合适的核函数和带宽大小，并使用交叉验证等技术来评估估计结果的准确性，并进一步优化参数选择，以获得更准确、可靠的估计结果。

在局部线性回归中，为了找到最合适的核密度函数，可以利用积分平方偏差、积分方差和积分均方误差等评价标准进行讨论。这些评价标准将帮助评估估计函数的好坏，并为选择合适的核密度函数提供必要的依据。通过采用这些方法，可以比较不同的核密度函数，并评估它们在实际应用中的效果，以更好地理解和利用局部线性回归方法。因此，在实际应用中，使用这些评价标准对选择正确的核密度函数进行评估是非常重要的。给出三种核密度函数的表达式：

1) Uniform核函数： $K\left(u\right)=\frac{1}{2},u\in \left[-1,1\right]$

2) Epanechnikov核函数： $K\left(u\right)=\frac{3}{4}\left(1-u^2\right)$

3) Biweight核函数： $K\left(u\right)=\frac{15}{16}{\left(1-u^2\right)}^2$

研究的重点是核函数，因此本文选择恒定带宽，即选择Ruppert (1995) [8] 以Plug-in方法得到的最优带宽：

$h_{MISE}={\left[\frac{8v_0{\displaystyle \int {\sigma }^2\left(x\right)\text{d}x}}{2{\mu }_2^{2}n{\displaystyle \int m^{″}{\left(x\right)}^{2}f\left(x\right)\text{d}x}}\right]}^{1/5}$

选择 $m\left(x\right)=x+2{\text{e}}^{-16x^2}$ ， $f\left(x\right)$ 是 $\left[-2,2\right]$ 上的Uniform密度函数，然后给出观测样本，采用局部线性回归的方法比较在三种不同核函数下的积分平方偏差、积分方差和积分均方误差。

4. 数据模拟

选择 $m\left(x\right)=x+2{\text{e}}^{-16x^2}$ ，随机变量X来自 $\left[-2,2\right]$ 上的Uniform密度，样本量为n = 100，n = 200，n = 500三中情形。 $\sigma =0.4$ ，随机误差 $\epsilon$ 服从标准正态分布，即 $E\left(\epsilon \right)=0$ ， $Var\left(\epsilon \right)=1$ ，则 $Y=m\left(x\right)+\sigma \left(x\right)\epsilon$ ，得到随机样本 $\left(X,Y\right)$ ，h为0.25。首先比较在Uniform核函数、Epanechnikov核函数、Biweight核函数下，局部线性回归的模拟值和真实值的拟合程度，其次使用局部线性回归方法在三种样本量下，计算不同核函数在100次模拟下对应的积分平方偏差，积分方差和积分均方误差。

实验结果表明，图1~3中无论是采用Epanechnikov核函数、Uniform核函数还是Biweight核函数，局部线性回归拟合的曲线与真实曲线都较为接近。这说明局部线性回归方法在不同核函数下具有很好的拟合效果。然而，当比较三种核函数的表现时，用Uniform核函数拟合的曲线更加接近真实曲线，并且误差相比于Epanechnikov核函数和Biweight核函数的拟合曲线要小。这表明在某些情况下，选择Uniform核函数作为局部线性回归方法的核函数可能更为合适。总的来说，本文对局部线性回归方法中不同核函数的选择进行了实验验证，得出了有价值的结论，这将为进一步改进该方法提供有益参考。

通过对表1的实验结果进行分析，可以得出以下结论：当核函数固定时，随着样本量的增加，积分均方偏差会减小，积分方差会增加，而积分均方误差则会减小。但需要注意的是，相比于积分均方偏差和积分均方误差，积分方差随着样本量的增加变化幅度较小，几乎可以忽略不计。在样本量固定的情况下，Biweight核函数的积分均方偏差最大，Epanechnikov核函数次之，Uniform核函数的积分均方偏差最小；Biweight核函数的积分方差最大，Epanechnikov核函数次之，Uniform核函数的积分方差最小。由于积分方差的值很小，对积分均方偏差的影响微乎其微，因此积分均方误差的变化趋势与积分均方偏差类似，即Biweight核函数的积分均方误差最大，Epanechnikov核函数次之，Uniform核函数的积分均方误差最小。尽管核函数能够有效避免“维数灾难”问题，但对于待估计函数的影响并不是很大。因此，在未要求核函数的情况下，可以适当选择易于计算的核函数以减少计算量。这些结论有助于更全面地了解局部线性回归方法在实际应用中的表现，并为其优化和改进提供重要参考。

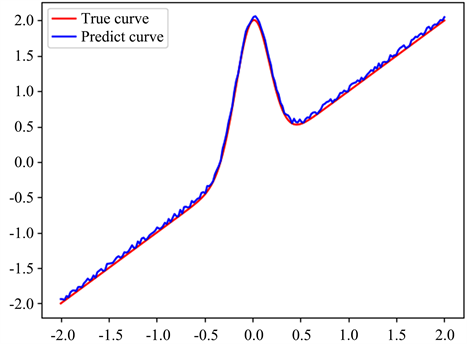
Figure 1. Degree to which the simulated values are fitted to the true values using local linear regression when the kernel function is the Epanechnikov kernel function

图1. 核函数为Epanechnikov核函数时，用局部线性回归模拟值与真实值拟合程度

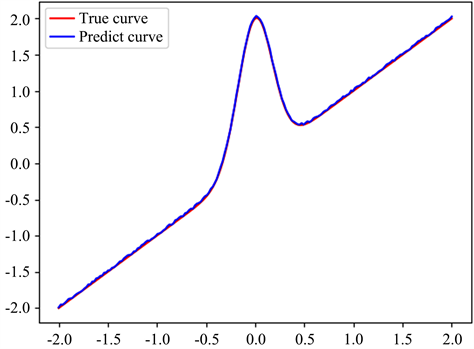
Figure 2. Degree to which the simulated values are fitted to the true values using local linear regression when the kernel function is a uniform kernel function

图2. 核函数为uniform核函数时，用局部线性回归模拟值与真实值拟合程度

Figure 3. Degree to which the simulated values are fitted to the true values using local linear regression when the kernel function is the Biweight kernel function

图3. 核函数为Biweight核函数时，用局部线性回归模拟值与真实值拟合程度

Table 1. Integral squared deviation, integral variance and integral mean square error of the kernel function for different sample sizes

表1. 核函数在不同样本量下的积分平方偏差，积分方差和积分均方误差

5. 结论

本文介绍了非参数回归方法中的局部线性回归，并强调了其在实际应用中的优点。虽然非参数回归方法有很多种，但是在实践中常常使用局部多项式回归这一方法。而局部线性回归则可以看作是局部多项式回归的特例，同时具备良好的渐近性质和收敛速度，此外其数值计算相对简单。这些优势使得局部线性回归成为非参数回归方法的重要分支之一，并且被广泛应用于各种领域，例如金融、医学和环境科学等。在实际应用中，局部线性回归的优点显得尤为突出，不仅能够提高模型预测的准确性，还能够提高模型的可解释性和可靠性，因此在理论和实践中都得到了广泛关注。本文主要研究了在局部线性回归方法下，不同核函数和样本量对积分均方偏差、积分方差和积分均方误差的影响。通过模拟实验，发现当核函数固定时，随着样本量的增加，积分均方偏差会减小，积分方差会增大，而积分均方误差则会减小；当样本量固定时，不论选择Biweight核函数、Epanechnikov核函数还是Uniform核函数，积分均方偏差、积分方差和积分均方误差之间的差别都不大。因此，在不要求核函数的情况下，可以选择相对简单的核函数，这有助于减少计算量。总的来说，本文的研究对于深入理解局部线性回归方法在不同条件下的表现和优化具有一定的参考价值。