空间相干性对电解质纳米二聚体散射特性的影响

Effect of Spatial Coherence on the Scattering Properties of a Dielectric Nanodimer

摘要: 本文研究一个电介质纳米二聚体在部分相干光激发下的散射特性。首先解析推导了该二聚体的耦合电偶极子模型，并计算了散射光的远场强度分布特性。我们发现入射光的空间相干性对该纳米结构的散射强度、散射分布图样、散射方向性等都有显著影响。我们的计算结果尤其表明，入射光的空间相干性与它的偏振态和波长之间会产生复杂的相互作用从而改变上述散射性质。进一步通过调节空间相干度的幅值和相位，实现了对二聚体散射的强度方向性调控，这在不考虑磁多极激发的情况下是较为罕见的。我们的研究方法和结果对于进一步开发纳米结构的散射功能具有潜在的价值。

Abstract: In this article we studied the scattering properties of a dielectric nanodimer excited by a partially coherent incident light. Far-field distributions of the intensity of scattered light were analyzed through both analytical derivations and numerical computations with the coupled electric dipole model. We found prominent effects of spatial coherence on the scattering strength, the scattering pattern and the scattering directivity. In particular, our computational results demonstrated com-plex interplays between the spatial coherence and the polarization and wavelength of incident light. Through tuning both the norm and phase of the degree of spatial coherence, we achieved evident transverse and directional scattering which were otherwise impossible without magnetic excitations. Our methods and findings in this study would be helpful in exploiting scattering functionalities using nanostructures.

1. 引言

纳米粒子，无论是排列成周期性阵列 [1] 还是组织成无需的团簇 [2] ，都展现出丰富的光学与电磁性质。这些性质进一步持续的激励各种新颖的光学现象和电磁器件的涌现，例如光学Anapole态 [3] 和超表面 [4] 。在各种各样的由纳米粒子构成的系统中，纳米二聚体由于其简单并且灵活的特点成为最具代表性的一种。它的简单性表现在它只由两个单独的纳米粒子组成，因此对它的散射特性要么可以得到解析的表达式，要么可以实现快速的数值计算。而其灵活性在于两个纳米粒子的材料、尺寸、形状以及它们之间的距离都可以灵活调节来实现截然不同的功能。科学家们已经利用纳米二聚体成功的实现了诸如表面增强拉曼散射 [5] ，位移测量 [6] ，手性感知 [7] 等技术。更为重要的是，纳米二聚体可能是能够反映和利用纳米粒子之间耦合特性的最小系统。粒子之间的这种耦合主要表现为每个粒子中多极子的互相激发。尤其是最近报道并受到广泛关注的现象如方向性散射 [8] 、横向散射 [9] 等都归因于粒子中激发起的一系列电多极子或者磁多极子之间的干涉效应 [10] 。

另一方面，纳米结构在光学中的现代应用越来越经常涉及到来自非相干或者部分相干光学的光波。例如，纳米粒子已经在太阳能电池增强光能收集方面发挥重要作用 [11] [12] ，而到达地表的阳光的相干宽度一般仅在几十个微米 [13] ，远小于粒子之间分开的距离。实际上已经有作者考虑了光波空间相干性在太阳能电池光能管理中的效应 [14] 。另外还有研究者揭示了部分相干性与吸收以及近红外辐射之间的关系 [15] 。在其他相关研究中，光的空间相干性也被证明会对辐射光源的方向性产生影响 [16] 。然而截至目前，光的相干性对纳米二聚体散射特性的影响还未见报道。本文的目的就是研究如光入射光是部分相干的，纳米二聚体的散射特性将怎样以及在何种程度上受到影响。为了便于解析分析，我们聚焦于研究由两个电介质材料的球形粒子构成的纳米二聚体。并且在这里忽略粒子中可能因材料折射率足够高而激发的磁多极子 [17] 。在下文中可以看到，这样一个耦合电偶极子模型可以很好的反映光的空间相干性对二聚体的远场辐射分布以及散射强度的显著效应。

2. 耦合电偶极子模型

假设一个纳米二聚体放置在介电常数为 ${ϵ}_0$ 的真空中。一个角频率为 $\omega$ 、波矢量为 $k$ 、振幅为 $E_0$ 的单色平面波照射该二聚体。在空间中的任意位置，总电场强度 $E$ 是入射光场与散射光场的电场强度之和，并且它满足如下的非齐次矢量赫姆霍兹方程 [18] ，

$\nabla \times \nabla \times E-k^{2}E=\frac{k^2}{{ϵ}_0}P.$ (1)

这里 $k=\omega /c=2\pi /\lambda$ 是光的波数，而c和 $\lambda$ 分别是光在真空中的速度和波长。矢量 $P$ 代表入射光在粒子中引起的电极化强度。用 $R_1$ 和 $R_2$ 表示两个粒子球心的位置。显然，每一个球形粒子感受到的光电场是入射光和另一个粒子散射光电场之和。这里我们假定两个球形粒子的半径远小于入射光波长，以至于可以忽略电场引起极化的高阶多极矩。假设这两个球的偶极子极化率分别为 ${\alpha }_1,{\alpha }_2$ ，两个球的电偶极矩分别为 $p_1=p\left(R_1\right)$ 和 $p_2=p\left(R_2\right)$ ，这两者之间满足一个自洽的方程组：

$\begin{array}{l}{p}_1={\alpha }_1\left[E_0\left(R_1\right)+\frac{k^2}{{ϵ}_0}\mathbb{G}\left(R_1,R_2\right)p_2\right],\\ p_2={\alpha }_2\left[E_0\left(R_2\right)+\frac{k^2}{{ϵ}_0}\mathbb{G}\left(R_2,R_1\right)p_1\right].\end{array}$ (2)

这里函数 $\mathbb{G}$ 表示自由空间的并矢格林函数。这里我们采用的符号习惯为它的第一变量表示场点位置，第二变量表示源的位置。该函数的具体形式为 [18] ，

$\mathbb{G}\left(r,r^{\prime }\right)=\left(\mathbb{I}+\frac{1}{k^2}\nabla \nabla \right)G\left(r,r^{\prime }\right)=\frac{\exp \left(ikR\right)}{4\pi R}\left[\left(1+\frac{ikR-1}{k^2{R}^2}\right)\mathbb{I}+\frac{3-3ikR-k^2{R}^2}{k^2{R}^2}\frac{RR}{R^2}\right],$ (3)

其中函数G是自由空间的标量格林函数：

$G\left(r,r^{\prime }\right)=\frac{\exp \left(ikR\right)}{4\pi R},$ (4)

公式(3)中的偏微分是对场点坐标进行的。符号 $\mathbb{I}$ 表示三维空间的单位张量，而 $R=r-r^{\prime }$ 表示从源点指向场点的矢量， $R=\left|R\right|$ 是它的长度。从公式(3)显然可以看出，张量格林函数 $\mathbb{G}$ 关于它的两个自变量是可互易的，所以在下文中不需要区分源点和场点的情况下我们将省去它的自变量。把公式(2)中的一个代入另一个可以得到两个电偶极矩的解：

$\begin{array}{l}\left[\mathbb{I}-{\alpha }_1{\alpha }_2{\left(\frac{k^2}{{ϵ}_0}\right)}^2{\mathbb{G}}^2\right]p_1={\alpha }_1{E}_0\left(R_1\right)+{\alpha }_1{\alpha }_2\frac{k^2}{{ϵ}_0}\mathbb{G}\left(R_1,R_2\right)E_0\left(R_2\right),\\ \left[\mathbb{I}-{\alpha }_1{\alpha }_2{\left(\frac{k^2}{{ϵ}_0}\right)}^2{\mathbb{G}}^2\right]p_2={\alpha }_2{E}_0\left(R_2\right)+{\alpha }_1{\alpha }_2\frac{k^2}{{ϵ}_0}\mathbb{G}\left(R_2,R_1\right)E_0\left(R_1\right).\end{array}$ (5)

从公式(5)不难发现，如果只考虑纳米粒子中电偶极子之间的耦合，那么它们的电偶极矩只由入射场和自由空间的张量格林函数决定。公式右边的第一项代表由入射场引起的极化部分，而第二项表示由另一个粒子的散射场引起的极化部分。结合公式(3)还可以发现，从一个粒子散射并到达另一个粒子的光的偏振态，只取决于连接两个粒子位置的矢量 $R_1-R_2$ 。

一旦通过公式(5)求出偶极矩 $p_1,p_2$ ，空间中任意一点 $r$ 处的散射光场就是 $p_1$ 和 $p_2$ 在 $r$ 处的辐射场之和：

$E_s\left(r\right)=\frac{k^2}{{ϵ}_0}\left[\mathbb{G}\left(r,R_1\right)p_1+\mathbb{G}\left(r,R_2\right)p_2\right].$ (6)

由于我们感兴趣的是远场的散射特性，也就是从原点到 $r$ 的距离远大于 $\left|R_{1,2}\right|$ ，所以在利用公式(5)求解电偶极矩时可以使用张量格林函数的近场近似，

${\mathbb{G}}_{\text{NF}}=\frac{\exp \left(ikR\right)}{4\pi R}\frac{1}{k^2{R}^2}\left(-\mathbb{I}+3RR/R^2\right),$ (7)

而当使用公式(6)计算散射场时，可利用张量格林函数的远场近似，

${\mathbb{G}}_{\text{FF}}=\frac{\exp \left(ikR\right)}{4\pi R}\left(\mathbb{I}-RR/R^2\right).$ (8)

在计算远场分布时，我们使用球坐标系，位置矢量 $r$ 在该坐标系下可写成

$r=\left(r\sin \theta \cos \varphi ,r\sin \theta \sin \varphi ,r\cos \theta \right),$ (9)

其中r是该位置到原点之间的距离，我们设定 $r=100\lambda$ 。角度 $\theta$ 和 $\varphi$ 分别是从z轴正向和x轴正向算起的极角和周向角。

3. 对称二聚体的散射

首先考虑一个由两个完全相同的球形粒子组成的二聚体。球的半径为a，折射率为n，与真空的相对折射率为 $m=n/n_0$ 。根据米散射理论，球形粒子的电偶极极化率由米散射系数 $a_1$ 给出：

${\alpha }_1={\alpha }_2=\alpha =\frac{6\pi i}{k^3}{a}_1,$ (10)

如果定义粒子尺寸参数 $x=a2\pi /\lambda$ ，那么米散射系数 $a_n$ 由下面的公式给出 [19] ：

$a_n=\frac{m^2{j}_n\left(mx\right){\left[x{j}_n\left(x\right)\right]}^{\prime }-j_n\left(x\right){\left[mx{j}_n\left(mx\right)\right]}^{\prime }}{m^2{j}_n\left(mx\right){\left[x{h}_n^{\left(1\right)}\left(x\right)\right]}^{\prime }-h_n^{\left(1\right)}\left(x\right){\left[mx{j}_n\left(mx\right)\right]}^{\prime }}.$ (11)

其中函数 $j_n\left(x\right)$ 和 $h_n^{\left(1\right)}\left(x\right)$ 分别是n阶第一类球贝塞尔函数和球汉克尔函数。公式中的符号'表示对圆括号中的变量求导。该公式对金属和电解质材料的球形粒子都适用。并且材料性质通过相对折射率m反映在米散射系数中。

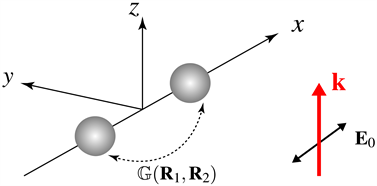
Figure 1. Geometry of the nanodimer and the incident plane wave

图1. 纳米二聚体与入射光的几何关系示意图

如图1所示，我们选择坐标系使二聚体的轴线沿x轴方向，而波矢量 $k$ 始终沿z轴方向。首先令入射光沿x方向偏振，即 $E_0\left(r\right)=E_0\left(r\right)\hat{x}$ 。当二聚体的整体尺寸远小于入射光波长时，可以认为入射光电场在整个二聚体的尺度范围内变化很小，可做近似 $E_0\left(R_1\right)\approx E_0\left(R_2\right)=E_0$ 。然而，两个球心处的光场可以是部分相干的，也就是当考虑统计平均时有，

$\langle E_0^{*}\left(R_1\right)E_0\left(R_2\right)\rangle =\left|E_0\left(R_1\right)\right|\left|E_0\left(R_2\right)\right|\eta \left(R_1,R_2\right).$ (12)

在上式中， $\eta =\left|\eta \right|\exp \left(i{\phi }_{\eta }\right)$ 称为归一化的相干函数，或者光场的空间相干度，它一般是个复数并且它的幅值满足 $0\le \left|\eta \right|\le 1$ 。如果入射光相干性很低，那么一般 $\eta$ 一般随 $\left|R_1-R_2\right|$ 变化很快。具有这种特点的光场一般称为准均匀的 [16] 。

对于这样的二聚体结构和入射光的偏振态，可以较容易的推测两个球的电偶极矩都只有x分量，通过公式(5)我们求出：

$\begin{array}{l}{p}_{1x}=\frac{1}{A}\left[\alpha E_0\left(R_1\right)+{\alpha }^2\frac{k^2}{{ϵ}_0}{\mathbb{G}}_{xx}{E}_0\left(R_2\right)\right],\\ p_{2x}=\frac{1}{A}\left[\alpha E_0\left(R_2\right)+{\alpha }^2\frac{k^2}{{ϵ}_0}{\mathbb{G}}_{xx}{E}_0\left(R_1\right)\right],\end{array}$ (13)

其中

$A=1-{\alpha }^2{\left(\frac{k^2}{{ϵ}_0}\right)}^2{\left({\mathbb{G}}^2\right)}_{xx}.$ (14)

将公式(13)代入公式(6)就可求出散射场。观察公式(13)可以比较直观的看出由于两个球的耦合产生的干涉效应。散射场是由 $p_{1x}$ 和 $p_{2x}$ 的辐射场叠加而成。每一个辐射场都含有部分相干的两部分，也就是公式右边的第一和第二项。这两项的权重因子分别是近场张量格林函数 ${\mathbb{G}}_{\text{NF}}\left(R_1,R_2\right)$ 和远场张量格林函数 ${\mathbb{G}}_{\text{FF}}\left(r,R_{1,2}\right)$ 。当我们计算任何可观测量——例如散射光强时，干涉效应将通过形如公式(12)的表达式出现。由此不难推测，如果这里的耦合模型中还包含电四极子或者磁偶极子和磁四极子，两个这些多极子的辐射叠加后也会带来类似的干涉效应，空间相干度同样会调制总的散射光强。所以说空间相干性的引入还适用于更复杂的耦合辐射问题。

Figure 2. Far field intensity distribution of scattered light in the x plane under the incidence of a x Polarized light. The direction of $\varphi =0$ coincides with x axis, the center of the nanodimer coincides the origin of the coordinate system. The two spheres have the same radius $a=75\text{nm}$ , the center distance

is 160 nm

图2. x线偏振光入射下xy平面内散射光强的远场分布。图中 $\varphi =0$ 方向与x轴重合。二聚体中心与坐标原点重合，两个球形粒子半径相等，为 $a=75\text{nm}$ ，中心距为160 nm。入射光波长为 $\lambda =450\text{nm}$ 。粒子折射率为 $n=4+0i$ 。为计算方便，在计算图中结果时设 $E_0\left(R_1\right)=E_0\left(R_2\right)=1$ 。图例中给出了不同曲线对应的空间相干度 $\eta$ 的取值

图2中给出了xy平面内散射光强的远场分布。从图2(a)可以看出，当固定空间相干度的幅值在 $\left|\eta \right|=0.5$ 时，远场散射强度明显小于完全相干的情况。然而，调节 $\eta$ 的相位不但显著改变了散射强度，还起到调控辐射方向的作用。更为独特的是，当把 $\eta$ 的相位符号时（ $\eta =\pm 0.5i$ ），两者的散射分布图样关于y轴对称。为此，我们进一步观察同时调节 $\eta$ 的幅值和相位带来的影响，如图2(b)所示。为了理解这些现象，把散射场的任一分量，例如第i分量 $E_{si}\left(r\right)$ 表达式写出：

$\begin{array}{c}{E}_{si}\left(r\right)=\frac{k^2}{{ϵ}_0}\left[{\mathbb{G}}_{ix}\left(r,R_1\right)p_{1x}+{\mathbb{G}}_{ix}\left(r,R_2\right)p_{2x}\right]\\ =\frac{1}{A}\left[\alpha {\mathbb{G}}_{ix}\left(r,R_1\right)+{\alpha }^2\frac{k^2}{{ϵ}_0}{\mathbb{G}}_{ix}\left(r,R_2\right){\mathbb{G}}_{xx}\left(R_2,R_1\right)\right]E_0\left(R_1\right)\\ +\frac{1}{A}\left[\alpha {\mathbb{G}}_{ix}\left(r,R_2\right)+{\alpha }^2\frac{k^2}{{ϵ}_0}{\mathbb{G}}_{ix}\left(r,R_1\right){\mathbb{G}}_{xx}\left(R_1,R_2\right)\right]E_0\left(R_2\right).\end{array}$ (15)

当利用公式(15)计算该分量光强 ${\left|E_{si}\right|}^2$ 时，将得到三项，前两项与入射光强 ${\left|E_0\left(R_1\right)\right|}^2$ 和 ${\left|E_0\left(R_2\right)\right|}^2$ 成正比，而第三项，即干涉项，包含空间相干度 $\eta$ 的实部。由于空间相干度和与它相乘的因子都为复数值，所以相干度的幅值与相位将共同决定干涉项的最终大小，从而影响总散射强度。

通过公式(15)还可以观察到入射光偏振方向对散射特性的影响。这一效应主要通过用于两个粒子耦合的张量格林函数 $\mathbb{G}\left(R_1,R_2\right)$ 来体现。结合公式(7)不难看出，这个传播子通过单位张量 $\mathbb{I}$ 把一个粒子上的电场映射到另一个粒子，同时还通过并矢 $RR,\left(R=R_1-R_2\right)$ 把一个粒子上的电场投影到另一个粒子上。所以入射光的偏振方向以及 $R$ 的方向决定了两个粒子之间的耦合。这种耦合作用与空间相干性的作用共同的影响会行程更新颖的散射特性。图3中给出了当入射光偏振沿y方向时在xy平面内的散射分布。

Figure 3. Far field intensity distribution of scattered light in the xy plane under the incidence of a y polarized light. Other parameters of the light and the nanodimer are the same of those in Figure 2

图3. y偏振光入射下xy平面内的远场散射光强分布。其他光波和纳米二聚体的参数与图2中相同

从图3可以容易地看出，除了随着相干度的不同散射分布花样变化之外，空间相干性效应还其他独特的特征。首先，从(a)和(b)两个图中都可以发现，部分相干光入射导致的散射强度都显著大于完全相干光照射的情况，这与入射光偏振沿x方向时形成鲜明对比。(a)图的结果表明，即使不改变相干度 $\eta$ 的幅值，而只改变其相位，散射强度和方向性也发生显著改变。如果相位符号发生变化，散射分布图样仍然呈对称性。但是这时由于散射具有明显方向性，所以这种对称性实际上实现了散射主瓣的方向翻转。(b)图的结果表明，尽管部分相干入射可以得到比完全相干更高的散射强度，但是提高空间相干度的幅值仍以可以提高散射主瓣方向的强度。而调节相干度的相位会同时影响散射主瓣和它相反方向的散射强度。在(b)图中比较不同的 $\eta$ 取值可以看出，从提高方向性来说，空间相干度可能存在一个最优的幅值与相位的匹配。

4. 非对称二聚体的散射

最后，我们考虑一个非对称的二聚体，即两个球形粒子大小不同时的散射特性。根据公式(10)，不同的尺寸导致这两个球形粒子具有不同的极化率系数。根据前文的讨论不难推测，空间相干性在调制散射强度以及方向性等方面应该与对称二聚体有类似的效应。然而根据公式(11)，米散射系数除了与粒子尺寸有关外，还通过尺寸参数 $x=a2\pi /\lambda$ 与入射光波长有关。为此我们选择 $\lambda =450\text{nm},630\text{nm}$ 这两种不同的波长来考察这个不对称二聚体的散射特性。这里入射光偏振仍设定为沿y方向。

Figure 4. Far field intensity distribution of scattered light from a non-Symmetric nanodimer under the incidence of a y polarized light. The direction of $\varphi =0$ coincides with the x axis. The radii of the two spheres are respectively $a_1=75\text{nm}$ , $a_2=115\text{nm}$. The centers of the two spheres are located on the x axis with coordinates $x_{1.2}=\pm 99\text{nm}$ . The refractive indices are the same $n=4+0i$ . The wavelengths of the incident light are (a) $\lambda =450\text{nm}$ and (b) $\lambda =630\text{nm}$

图4. y偏振光照射下非对称纳米二聚体散射光在xy平面的远场光强分布。 $\varphi =0$ 方向与x轴重合。两个球形例子的半径分别为 $a_1=75\text{nm}$ , $a_2=115\text{nm}$ 。两个球的球心位于x轴，坐标为 $x_{1.2}=\pm 99\text{nm}$ 。两个球的折射率相同，为 $n=4+0i$ 。入射光波长为(a) $\lambda =450\text{nm}$ (b) $\lambda =630\text{nm}$

图4给出了远场散射光强分布。首先比较(a)图与图3(b)，两者除了二聚体的结构不同之外，其他参数都相同。从中不难发现空间相干性与二聚体结构之间也有比较独特的相互作用。具体来说，当空间相干度 $\eta =0.5i$ 时，对称二聚体形成关于y轴非对称的散射分布花样，而非对称二聚体却得到一个几乎对称的散射分布花样。而对照 $\eta =0.8i$ 和 $\eta =0.8{\text{e}}^{i2\pi /3}$ 连个参数，发现本来散射强度不同的两个散射分布变成了散射强度几乎相等、并且关于y轴对称的分布。而对照图4(a)和图4(b)可以看出，由于入射波长不同，干涉效应造成的结果也显著不同，在 $\lambda =630\text{nm}$ 时，相干入射和部分相干如何得到的散射强度呈现出巨大反差。

5. 结论

本文在耦合偶极子模型下，通过解析推到和计算研究了由两个电介质球体构成的对称和非对称结构的纳米二聚体的散射特性。通过在入射光中引入部分空间相干性，我们发现光的空间相干度对于这种结构的散射强度、远场散射分布和散射方向性都有显著影响。这种相干性效应的机理进一步表现为它与入射光的偏振态和波长混合为一种复杂的调制作用。特别的，研究发现通过调节空间相干度的幅值和相位可以明显的散射方向性，这在一般的耦合电偶极子 [20] 散射问题中是较难实现的。本研究的方法和结果对于发展利用纳米结构控制光场的技术具有潜在的价值。

基金项目

本研究得到广东省自然科学基金项目(2016A030307026)，国家基础研究计划项目(22078072)和广东省教育厅特色创新项目(2021ZDZX4060)的资助。