1. 引言
水流以某种特定流速流经桥墩时,会在桥墩后出现旋转方向相反、周期性排列、交替脱落的双列涡阵结构,这就是著名的卡门涡街,也是一种常见的圆柱绕流现象。圆柱绕流现象在自然界和工程实践中都十分常见,如空气绕过烟囱、海风吹过海岛和海底输运管道等等。圆柱绕流是一个经典的流体力学问题,一定量的流体流经钝体结构物时,上游部分流断面缩减,流速增加,压强减小。下游部分的流体受壁面的摩擦阻力作用和逆压梯度的减速作用,其压强大于上游流体,出现回流。回流的流体质点使边界层脱离固体表面,形成漩涡,发生圆绕流现象。由于圆柱绕流过程的受力复杂,对其流动现象物理本质的理解或传统的实验研究仍不完整。
针对圆柱绕流问题的研究,主要通过试验模拟和数值模拟对流体运动进行仿真分析。1985年,伊杰里奇克试验模拟了均匀来流条件下的光滑单圆柱绕流现象,得到了阻力系数与雷诺数之间的关系曲线 [1] 。Bouard [2] 等人通过试验研究了雷诺数在40-9500之间的圆柱流动,测量出边界层分离点以及柱后对称轴线上的速度、升力、阻力系数等等。随着计算机技术的发展,越来越多的数值计算方法被应用到圆柱绕流的仿真模拟中。直接求解流体运动方程的方法是直接模拟法,该方法可以精确地获得流体在任何时刻、任何空间位置的瞬态信息。但由于对时间和空间分辨率,及计算机的性能都有较强的要求,通常只用于雷诺数较低的湍流运动,如槽道或圆管湍流。对于雷诺数较大的湍流现象,1886年雷诺 [3] 等人提出雷诺平均法,即RANS法。该方法通过对方程进行时间统计平均,用平均运动代替各尺度的湍流脉动,从而减少计算和内存需求。马金花 [4] 等人构造了求解雷诺平均NS方程的有限元数值格式,得到了围绕单圆柱流动的流体随时间变化的速度矢量图和非定常力系数等,和实验结果具有合理的一致性。但RANS法使用的平均运动会失去脉动运动细节,因此1992年苑明顺 [5] 等人提出大涡模拟方法(LES法),通过对流场中的大尺度变量进行直接模拟,对小尺度变量采用亚格子雷诺应力模型模拟,得到单圆柱绕流二维数值模拟的升力系数、阻力系数和柱面时均压力分布等比较合理的流动参数,确定了大涡模拟的有效性。为进一步解决大涡模拟边界层的增长和分离不准问题,1963年Smagorinsky [6] 首次将RANS模型与LES模型结合,提出分离涡模拟法,即DES法。该方法的基本思想是在近壁面的附面层采用计算量较小的雷诺平均方法;在远离物面的区域,用网格尺度的常数倍代替耗散项的湍流尺度参数,构造大涡模拟的亚格子模型,对大尺度分离涡进行高精度模拟。分离涡模拟法目前已经应用于圆球和机翼等绕流运动的仿真中,并得到了较好的效果 [7] 。
本文采用基于SST方程的DES湍流模型,分析不同雷诺数条件下二维圆柱绕流的湍流尾迹,计算升力系数、阻力系数和斯特罗哈数等参数,得到尾涡变化与雷诺数之间的关系,并与相关文献上的实验和计算数据比较验证。
2. 模型与求解
2.1. 数学模型
圆柱绕流等粘性不可压缩流体的流动规律可以用Navier-Stokes方程描述。Navier-Stokes方程简称NS方程,是基于牛顿第二定律、质量守恒定律和动量守恒定律等基本物理规律建立的偏微分方程。在直角坐标系下,二维无热传导的Navier-Stokes连续方程和动量方程分别表示为
(1)
(2)
其中,
是速度函数在
方向的分量;
是压力函数;
是流体密度;
是流体运动粘性系数。
基于
SST两方程湍流模型方程如下
(3)
(4)
(5)
其中
是湍流生成项,方程(3)~(4)中的参数和均常数均与文献 [8] 一致。
将方程(4)中的湍流尺度参数
用
代替即可得到DES模型,其中
,
表示网格单元尺寸的最大值。如果
,该模型即为SST两方程湍流模型;如果
,该模型即
为大涡模拟模型。
2.2. 求解方法
针对分离涡模拟湍流方程模型,构造有限体积离散算法并求解。有限体积法的主要思想是对几何区域进行网格剖分,使每个网格节点周围都有互不重复的体积单元或控制单元;将待求解的微分方程在每一个体积单元内对时间和空间作积分,得到一组表示物理量守恒的离散方程。对于方程模型的对流项采用QUICK格式,扩散项采用二阶中心差分格式,压力速度耦合迭代采用SIMPLE算法。
3. 数值实验
3.1. 物理工况
物理模型如图1所示,取长和宽分别是250 mm和100 mm的矩形区域为计算域,矩形左侧为上游边界,右侧为下游边界。固定直径为10 mm的圆柱,圆柱的圆心分别距上游边界50 mm,距下游边界200 mm,距上下边界均为50 mm。流体介质是水,在20摄氏度的环境下,水的密度是
,动力粘性系数是
。
3.2. 实验设置
3.2.1. 网格划分
选取四边形结构化网格对计算域进行离散化。由于圆柱附近的来流流动变化大、流动情况复杂,为保证数值模拟的精度,采用加密方法处理网格。以圆柱为中心,分别在距离上游边界、下游边界和上下边界上选取宽度为17.68 mm的带宽区域为网格加密区域,如图2所示。圆柱周围布置边界层网格,以圆柱表面为第一层,向外均匀划分35层边界,如图3所示。在远场或流动均匀的其他流场区域以采用相对稀疏的网格划分方法,以减少计算负担。
3.2.2. 边界条件
在Fluent界面中,将上游边界设置为速度入口边界条件,下游边界设置为流动出口边界条件,上、下侧边界设置为对称边界,圆柱表面设置为无滑移壁面边界条件。其中速度入口边界条件根据雷诺数的
大小调整,来流速度与雷诺数之间的关系为
,其中
为流体密度,
为来流速度,
为圆柱
直径,
为流体的动力粘性系数。本文分析雷诺数为20,100,2300,3900等四种情况下的流场情况,因此分别设定流体速度为0.002 m/s,0.01 m/s,0.23 m/s和0.39 m/s。
3.3. 实验结果
3.3.1. 尾流的涡量图和流线图
图4和图5分别是不同雷诺数条件下,定常来流绕过单圆柱后尾流产生的涡量图和流线图。图4(a)和图5(a)可以看出,在雷诺数Re = 20时,流体流经圆柱后在其后方形成一对稳定的、对称的弗普尔旋涡。随着雷诺数的增大,两个弗普尔旋涡被拉伸增大,一侧旋涡的强度会超过另一侧,不再保持对称关系,使得漩涡中心逐渐脱离圆柱表面。如图4(b)和图5(b)所示,在雷诺数Re = 100时,弗普尔旋涡已经完全脱离圆柱表面,并在圆柱后的尾流区出现尾涡生成、发展、脱落和耗散的过程,逐渐形成两排周期摆动、交错的旋涡,即卡门涡街现象。此时的流场处于层流状态。

 (a) Re = 20 (b) Re = 100
(a) Re = 20 (b) Re = 100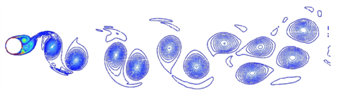
 (c) Re = 2300 (d) Re = 3900
(c) Re = 2300 (d) Re = 3900
Figure 4. Wake vorticity diagram at different Reynolds numbers
图4. 不同雷诺数下的尾流涡量图
当雷诺数增大到Re = 2300时,如图4(c)和图5(c)所示,旋涡之间的间距逐渐变小,旋涡脱落的周期逐渐缩短,尾流振荡的振幅也逐渐增大,在脱落过程中开始出现不对称现象,此时流场处于由层流到湍流的过渡态。当雷诺数Re = 3900时,在图4(d)和图5(d)中可以观察到尾涡不再具有对称性,涡的大小和脱落的位置时间都具有一定的随机性,此时近似于湍流状态。

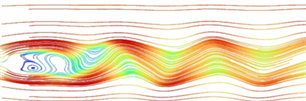 (a) Re = 20 (b) Re = 100
(a) Re = 20 (b) Re = 100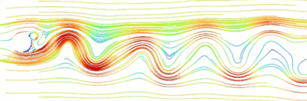
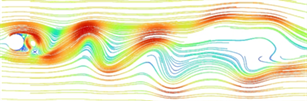 (c) Re = 2300 (d) Re = 3900
(c) Re = 2300 (d) Re = 3900
Figure 5. Wake streamline diagram at different Reynolds numbers
图5. 不同雷诺数下的尾流线图
3.3.2. 升力系数、阻力系数和斯特劳哈尔数
本文通过计算升力系数
、阻力系数
和特劳哈尔数
分析圆柱绕流的尾迹的发展规律。升力系数是指物体所受到的升力与气流动压和参考面积的乘积之比。阻力系数是指物体所受到的阻力与气流动压和参考面积的乘积之比,特劳哈尔数是指非稳态运动的惯性力与惯性力之比。其计算公式分别为
(6)
(7)
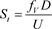 (8)
(8)
其中,
为单位长度圆柱在来流方向受到的合力,
为垂直于来流方向受到的合力,
为尾涡的脱落频率。
图6表示在雷诺数Re取20、100、2300、3900条件下升力系数和阻力系数的时程曲线。图中可以看出,在不同雷诺数下,阻力系数恒为正数,说明圆柱受到的推力与来流方向一致。在雷诺数Re = 20时,升力系数恒为零,阻力系数趋于某个固定值,说明流体经过圆柱后没有受到垂直于来流方向的力。在雷诺数Re = 100时,升力系数以相同振幅,围绕零值进行上下、周期性振荡,是层流的典型特征。此时的阻力系数出现轻微振荡,但仍然趋于稳定值。雷诺数继续增大到Re = 2300、3900时,升力系数的振幅出现明显变化,振荡的周期性减弱,阻力系数也出现脉动变化,不再趋于某个稳定值,逐渐出现湍流特征。与雷诺数Re = 2300相比,雷诺数Re = 3900时的升力系数和阻力系数的变化幅度都更大,变化周期都更短。
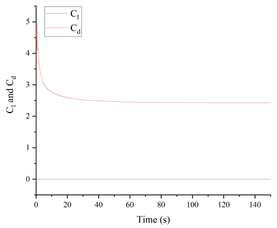
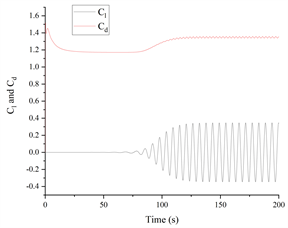 (a) Re = 20 (b) Re = 100
(a) Re = 20 (b) Re = 100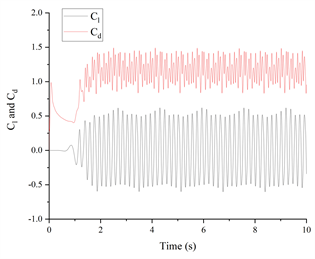
 (c) Re = 2300 (d) Re = 3900
(c) Re = 2300 (d) Re = 3900
Figure 6. Time history curves of lift coefficient and drag coefficient
图6. 升力系数和阻力系数的时程曲线
图7(a)和图7(b)分别表示升力系数和阻力系数随着雷诺数变化的变化趋势。由图中可以看出,升力系数随雷诺数的增大而增大,阻力系数随雷诺数的增大而减小。当雷诺数越来越大时,升力系数和阻力系数的变化幅度越来越小,曲线最终都逐渐趋于平缓。

 (a) 升力系数 (b) 阻力系数
(a) 升力系数 (b) 阻力系数
Figure 7. Variation trend of lift coefficient and drag coefficient with Reynolds number
图7. 升力系数和阻力系数随雷诺数变化的变化趋势
进一步对升力系数进行FFT分析,得到尾涡脱落频率,由计算公式(8)可以得到斯特劳哈尔数。表1是斯特劳哈尔数的计算结果与文献对比情况。当雷诺数Re = 20时,流体流经圆柱后没有出现尾涡脱落的现象,不存在尾涡脱落频率,因此不存在斯特劳哈尔数。当雷诺数Re = 2300和3900时,本文的计算结果比文献的数据偏大。这是因为在雷诺数较高时,尾涡脱落已经出现三维效应,需应用三维模型计算,应用二维的简化模型会使误差增大。

Table 1. Comparison between the calculation results of Strouhal number and the literature
表1. 斯特劳哈尔数的计算结果与文献对比
4. 总结
本文提出基于SST方程的分离涡模拟DES算法求解二维单圆柱绕流问题。结合计算流体力学软件Fluent,绘制出圆柱绕流的尾迹流线图和涡量图,计算升力系数、阻力系数和斯特劳哈尔数,分析不同雷诺数条件下的尾流规律。数值结果表明,在低雷诺数条件下,圆柱绕流产生的尾涡具有较强的对称性和周期性,升力系数稳定于确定值,阻力系数呈周期性振荡,符合层流的典型特征。当雷诺数过渡到亚临界区时,尾涡脱落的对称性减弱,随机性增强,升力系数不再趋于某个稳定值,阻力系数的振荡幅度增大,周期性降低。当雷诺数开始向湍流状态转变时,尾涡变化的随机性更强,升力系数和阻力系数的脉动幅度更大,振荡周期更短,符合湍流特征。
参考文献