一类趋化消耗模型解的整体有界性

Global Boundedness of Solution to a Chemotaxis-Consumption Model

摘要: 趋化描述了生物有机体受化学信号刺激所产生的偏向性运动，它在生物学、化学、医学等学科领域有着广泛的应用。本文研究齐次Neumann边界条件下的具次线性敏感及带logistic源的趋化消耗模型：，其中μ,χ > 0，r∈ℝ，α∈(0,1)和k > 1。在一维情形下，模型存在整体有界的古典解。

Abstract: Chemotaxis describes the biased movement of biological organisms stimulated by chemical signals. It is widely used in biology, chemistry, medicine and other fields. In this paper, a sublinear sensitive chemotactic-consumption model with logistic source under homogeneous Neumann boundary conditions is studied:, where μ,χ > 0, r∈ℝ, α∈(0,1) and k > 1. In the one-dimensional case, the model has a globally bounded classical solution.

1. 前言

上世纪70年代，Keller和Segel提出了生物趋化模型，它简单而又直观地刻画了生物有机体受化学信号刺激所产生的趋向性运动，在生物学、医学、环境科学等领域有着重要的应用。对于如下带logistic源的趋化消耗模型：

$\{\begin{array}{l}{u}_t=\Delta u-\chi \nabla \cdot \left(\frac{u}{v^{\alpha }}\nabla v\right)+ru-\mu u^2,x\in \Omega ,t>0,\hfill \\ v_t=\Delta v-uv,x\in \Omega ,t>0,\hfill \\ \frac{\partial u}{\partial \nu }=\frac{\partial v}{\partial \nu }=0,x\in \partial \Omega ,t>0,\hfill \\ u\left(x,0\right)=u_0\left(x\right),v\left(x,0\right)=v_0\left(x\right),x\in \Omega ,\hfill \end{array}$ (1.1)

其中 $\text{Ω}\in {ℝ}^n\left(n\ge 1\right)$ 为有界光滑区域， $\chi >0$ 代表趋化强度， $\alpha \in \left[0,1\right]$ ，并且logistic源中 $r\in ℝ$ ， $\mu >0$ 。 $u,v$ 分别表示细胞密度和氧气的浓度。另外，初始数据 $u_0\in C^0\left(\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}\right)$ 和 $v_0\in W^{1,\infty }\left(\text{Ω}\right)$ 非负。

现回顾模型(1.1)的相关结论。若 $\alpha =0$ ，文献 [1] 证明了当 $r>0,0<{\Vert v_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}\le \frac{1}{6\left(n+1\right)\chi }$ 时，模型存在全局有界的古典解；当 $\mu$ 充分大时文献 [2] 建立了模型古典解的整体有界性，并且 $r>0$ 时收敛到 $\left(\frac{r}{\mu },0\right)$ 。

若 $\alpha =1$ ，当 $n=2,r\le 0,\mu >{\mu }_{*}\left(\chi \right)>0$ 或 $r>0$ 且对 $\mu$ 再进行限制，文献 [3] 得到了模型(1.1)古典解在时间上的有界性和长时间行为；当 $r\ge 0$ ，文献 [4] 证明了 $n=1$ 或 $n\ge 2,\chi <\sqrt{2/n}$ 且 $\mu >\left(n-2\right)/2n$ 古典解的整体有界性。另外，将(1.1)中第一个方程变成拟线性形式： $u_t=\nabla \cdot \left(D\left(u\right)\nabla u\right)-\nabla \cdot \left(uS\left(x,u,v\right)\cdot \nabla v\right)$ ，其中

$D\left(u\right)\ge k_D{u}^{m-1},\left|S\left(x,u,v\right)\right|\le \frac{S_0\left(v\right)}{v^{\alpha }}$ ( $S_0$ 是非减的)，并且 $k_D>0,m>1,\alpha \ge 0$ ，文献 [5] 证明了当 $m>\frac{3n-2}{2n},\alpha \in \left[0,1\right)$ 时，系统存在整体有界的古典解。

本文受以上结论启发，研究一维情形下带logistic源及具次线性敏感的趋化消耗模型：

$\{\begin{array}{l}{u}_t=u_{xx}-\chi {\left(\frac{u}{v^{\alpha }}{v}_x\right)}_x+ru-\mu u^k,x\in \Omega ,t>0,\hfill \\ v_t=v_{xx}-uv,x\in \Omega ,t>0,\hfill \\ u_x=v_x=0,x\in \partial \Omega ,t>0,\hfill \\ u\left(x,0\right)=u_0\left(x\right),v\left(x,0\right)=v_0\left(x\right),x\in \Omega ,\hfill \end{array}$ (1.2)

其中 $\mu$ ， $\chi >0$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ 和 $k>1$ ， $\text{Ω}\in ℝ$ 为有界区间。

根据以上假设，可以得到系统(1.2)古典解的整体有界性。

定理1.1 设 $\chi >0$ ， $r\in ℝ$ ， $\alpha ,\beta \in \left(0,1\right)$ 和 $k>1$ 。有

${\Vert u\Vert }_{L^{\infty }\left(\text{Ω}\right)}+{\Vert v\Vert }_{W^{1,\infty }\left(\text{Ω}\right)}+{\Vert \frac{v_x}{v^{\beta }}\Vert }_{L^{\infty }\left(\text{Ω}\right)}\le C_{\star },t>0,$ (1.3)

其中 $C_{\star }>0$ 。

注 文献 [4] 证明了一维情形下，当 $r\ge 0,\alpha =1,k=2$ 时，模型古典解的整体有界性。与文献 [4] 不同，若 $r\in ℝ$ ，定理1.1证明了 $\alpha \in \left(0,1\right)$ 及 $k>1$ 时模型古典解的整体有界性。

2. 预备知识

根据Banach不动点理论，可以得到如下古典解局部存在性，参见 [4] 。

引理2.1 假设 $u_0\in C^0\left(\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}\right)$ 和 $v_0\in W^{1,\infty }\left(\text{Ω}\right)$ 是非负的。若 $\mu$ ， $\chi >0$ ， $k>1$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ ，则存

在 $T_{\max }\in \left(0,\infty \right]$ 及唯一非负函数 $\left(u,v\right)\in {\left(C^0\left(\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}\times \left[0,T_{\max }\right)\right)\cap C^{2,1}\left(\text{<mover accent="true"> Ω <mo> ¯ </mo> </mover>}\times \left(0,T_{\max }\right)\right)\right)}^2$ 在古典解意义下满足系统(1.2)。另外，当 $T_{\max }<\infty$ 时， ${\lim }_{t\to T_{\max }}{\Vert u\Vert }_{L^{\infty }\left(\text{Ω}\right)}=\infty$ 。

引理2.2 设 $\mu$ ， $\chi >0$ ， $k>1$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ ，则

${\displaystyle {\int }_{\text{Ω}}u\left(\cdot ,t\right)\text{d}x}\le \max \left\{{\displaystyle {\int }_{\text{Ω}}{u}_0\text{d}x},\left|\text{Ω}\right|{\left(\frac{\left|r\right|}{\mu }\right)}^{\frac{1}{k-1}}\right\},t\in \left(0,T_{\max }\right),$ (2.1)

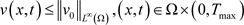(2.2)

证明 根据(1.2)的第一个方程，知

${\displaystyle {\int }_{\text{Ω}}{u}_t\text{d}x}=r{\displaystyle {\int }_{\text{Ω}}u\text{d}x}-\mu {\displaystyle {\int }_{\text{Ω}}{u}^k\text{d}x},t\in \left(0,T_{\max }\right)$

由Hölder不等式有

${\displaystyle {\int }_{\text{Ω}}{u}_t\text{d}x}\le r{\displaystyle {\int }_{\text{Ω}}u\text{d}x}-\frac{\mu }{{\left|\text{Ω}\right|}^{k-1}}{\left({\displaystyle {\int }_{\text{Ω}}u\text{d}x}\right)}^k,t\in \left(0,T_{\max }\right).$

应用伯努利不等式即得(2.1)。由抛物方程的极值原理易得(2.2)。

3. 主要结果

引理3.1 设 $\mu$ ， $\chi >0$ ， $k>1$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ 。若 $p>1$ ，则

$\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}+\frac{2\left(p-1\right)}{p}{\displaystyle {\int }_{\text{Ω}}{\left|{\left(u^{\frac{p}{2}}\right)}_x\right|}^2\text{d}x}\le \frac{p\left(p-1\right){\chi }^2}{2}{\displaystyle {\int }_{\text{Ω}}{u}^p{v}^{-2\alpha }{v}_x^2\text{d}x}+pr{\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}-p\mu {\displaystyle {\int }_{\text{Ω}}{u}^{k+p-1}\text{d}x},\\ t\in \left(0,T_{\max }\right).\end{array}$ (3.1)

证明 根据(1.2)的第一个方程，利用分部积分及Young不等式，知

$\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}=-p\left(p-1\right){\displaystyle {\int }_{\text{Ω}}{u}^{p-2}{u}_x^2\text{d}x}+p\left(p-1\right)\chi {\displaystyle {\int }_{\text{Ω}}{u}^{p-1}{v}^{-\alpha }{u}_x{v}_x\text{d}x}\\ +pr{\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}-p\mu {\displaystyle {\int }_{\text{Ω}}{u}^{k+p-1}\text{d}x}\\ \le -\frac{2\left(p-1\right)}{p}{\displaystyle {\int }_{\text{Ω}}{\left|{\left(u^{\frac{p}{2}}\right)}_x\right|}^2\text{d}x}+\frac{p\left(p-1\right){\chi }^2}{2}{\displaystyle {\int }_{\text{Ω}}{u}^p{v}^{-2\alpha }{v}_x^2\text{d}x}\\ +pr{\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}-p\mu {\displaystyle {\int }_{\text{Ω}}{u}^{k+p-1}\text{d}x},t\in \left(0,T_{\max }\right).\end{array}$

将上式进行移项即得(3.1)。

根据文献 [5] 中引理3.3，3.4和3.5，有

引理3.2 设 $\mu$ ， $\chi >0$ ， $k>1$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ 。若 $q\ge 2$ ，则存在 $c_i\left(q\right)>0\left(i=1,\cdots 4\right)$ ，使得

$\begin{array}{l}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^q\text{d}x}+c_1{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^{q-2}{\left|v_{xx}\right|}^2\text{d}x}+c_2{\displaystyle {\int }_{\text{Ω}}{v}^{-q-1}{v}_x^{q+2}\text{d}x}\\ \le c_3{\displaystyle {\int }_{\text{Ω}}v\text{d}x}+c_4{\displaystyle {\int }_{\text{Ω}}u{v}^{-q+2}{v}_x^{q-2}\left|v_{xx}\right|\text{d}x},t\in \left(0,T_{\max }\right).\end{array}$ (3.2)

引理3.3 设 $\mu$ ， $\chi >0$ ， $k>1$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ 。定义

$F={\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^q\text{d}x}.$

若 $p>1$ ， $q\ge 2$ ，则存在 $\text{Γ}=\text{Γ}\left(p,q,\chi \right)>0$ ，使得

$\begin{array}{l}F+F^{\prime }+\frac{2\left(p-1\right)}{p}{\displaystyle {\int }_{\text{Ω}}{\left|{\left(u^{\frac{p}{2}}\right)}_x\right|}^2\text{d}x}\le \text{Γ}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{p\left(q+2\right)}{q}}{v}^{\frac{2\left(q+1\right)-2\left(q+2\right)\alpha }{q}}\text{d}x}+\text{Γ}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{q+2}{2}}v\text{d}x}\\ +\left(c_3+{\left(\frac{3}{c_2}\right)}^{\frac{q}{2}}\right){\displaystyle {\int }_{\text{Ω}}v\text{d}x}+c_5,t\in \left(0,T_{\max }\right).\end{array}$ (3.3)

证明 将(3.1)与(3.2)相加，有

$\begin{array}{l}F+F^{\prime }+\frac{2\left(p-1\right)}{p}{\displaystyle {\int }_{\text{Ω}}{\left|{\left(u^{\frac{p}{2}}\right)}_x\right|}^2\text{d}x}+c_1{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^{q-2}{\left|v_{xx}\right|}^2\text{d}x}+c_2{\displaystyle {\int }_{\text{Ω}}{v}^{-q-1}{v}_x^{q+2}\text{d}x}\\ \le \frac{p\left(p-1\right){\chi }^2}{2}{\displaystyle {\int }_{\text{Ω}}{u}^p{v}^{-2\alpha }{v}_x^2\text{d}x}+\left(pr+1\right){\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}-p\mu {\displaystyle {\int }_{\text{Ω}}{u}^{k+p-1}\text{d}x}+c_3{\displaystyle {\int }_{\text{Ω}}v\text{d}x}\\ +c_4{\displaystyle {\int }_{\text{Ω}}u{v}^{-q+2}{v}_x^{q-2}\left|v_{xx}\right|\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^q\text{d}x},t\in \left(0,T_{\max }\right)\end{array}$ (3.4)

由Young不等式，存在 $c_5>0$ ，有

$\begin{array}{c}\frac{p\left(p-1\right){\chi }^2}{2}{\displaystyle {\int }_{\text{Ω}}{u}^p{v}^{-2\alpha }{v}_x^2\text{d}x}\le {\left(\frac{3}{c_2}\right)}^{\frac{2}{q}}{\left(\frac{p\left(p-1\right){\chi }^2}{2}\right)}^{\frac{q+2}{q}}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{p\left(q+2\right)}{q}}{v}^{\frac{2\left(q+1\right)-2\left(q+2\right)\alpha }{q}}\text{d}x}\\ +\frac{c_2}{3}{\displaystyle {\int }_{\text{Ω}}{v}^{-q-1}{v}_x^{q+2}\text{d}x},\end{array}$ (3.5)

$\begin{array}{c}{c}_4{\displaystyle {\int }_{\text{Ω}}u{v}^{-q+2}{v}_x^{q-2}\left|v_{xx}\right|\text{d}x}\le c_1{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^{q-2}{\left|v_{xx}\right|}^2\text{d}x}+\frac{c_4{}^2}{4c_1}{\displaystyle {\int }_{\text{Ω}}{u}^2{v}^{-q+3}{v}_x^{q-2}\text{d}x}\\ \le c_1{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^{q-2}{\left|v_{xx}\right|}^2\text{d}x}+\frac{c_2}{3}{\displaystyle {\int }_{\text{Ω}}{v}^{-q-1}{v}_x^{q+2}\text{d}x}\\ +{\left(\frac{3}{c_2}\right)}^{\frac{q-2}{4}}{\left(\frac{c_4{}^2}{4c_1}\right)}^{\frac{q+2}{4}}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{q+2}{2}}v\text{d}x},\end{array}$ (3.6)

${\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^q\text{d}x}\le \frac{c_2}{3}{\displaystyle {\int }_{\text{Ω}}{v}^{-q-1}{v}_x^{q+2}\text{d}x}+{\left(\frac{3}{c_2}\right)}^{\frac{q}{2}}{\displaystyle {\int }_{\text{Ω}}v\text{d}x},$ (3.7)

$\left(pr+1\right){\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}\le p\mu {\displaystyle {\int }_{\text{Ω}}{u}^{k+p-1}\text{d}x}+c_5.$ (3.8)

取 $\text{Γ}=\max \left\{{\left(\frac{3}{c_2}\right)}^{\frac{2}{q}}{\left(\frac{p\left(p-1\right){\chi }^2}{2}\right)}^{\frac{q+2}{q}},{\left(\frac{3}{c_2}\right)}^{\frac{q-2}{4}}{\left(\frac{c_4{}^2}{4c_1}\right)}^{\frac{q+2}{4}}\right\}$ ，将(3.5)，(3.6)，(3.7)，(3.8)代入到(3.4)中可得(3.3)。

引理3.4 设 $k>1$ ， $\mu ,\chi >0$ ， $r\in ℝ$ ， $\alpha \in \left(0,1\right)$ 。对于 $p,q>1$ ，存在 $C_0>0$ ，使得

${\displaystyle {\int }_{\text{Ω}}{u}^p\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{v}^{-q+1}{v}_x^q\text{d}x}\le C_0,t\in \left(0,T_{\max }\right).$ (3.9)

证明 取 $p>\max \left\{1,\frac{4\alpha -3}{2-2\alpha }\right\}$ ， $\max \left\{\frac{2\alpha -1}{1-\alpha },p\right\}<q<2+2p$ 。根据引理2.2与Gagliardo-Nirenberg不等

式及Young不等式，有

$\begin{array}{c}\text{Γ}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{p\left(q+2\right)}{q}}{v}^{\frac{2\left(q+1\right)-2\left(q+2\right)\alpha }{q}}\text{d}x}\le \text{Γ}{\Vert v_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}^{\frac{2\left(q+1\right)-2\left(q+2\right)\alpha }{q}}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{p\left(q+2\right)}{q}}\text{d}x}=\text{Γ}{\Vert v_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}^{\frac{2\left(q+1\right)-2\left(q+2\right)\alpha }{q}}{\Vert u^{\frac{p}{2}}\Vert }_{L^{\frac{2\left(q+2\right)}{q}}\left(\text{Ω}\right)}^{\frac{2\left(q+2\right)}{q}}\\ \le c_6{\Vert {\left(u^{\frac{p}{2}}\right)}_x\Vert }_{L^2\left(\text{Ω}\right)}^{\frac{2\left(q+2\right)}{q}a}{\Vert u^{\frac{p}{2}}\Vert }_{L^{\frac{2}{p}}\left(\text{Ω}\right)}^{\frac{2\left(q+2\right)}{q}\left(1-a\right)}+c_6{\Vert u^{\frac{p}{2}}\Vert }_{L^{\frac{2}{p}}\left(\text{Ω}\right)}^{\frac{2\left(q+2\right)}{q}}\\ \le c_7{\Vert {\left(u^{\frac{p}{2}}\right)}_x\Vert }_{L^2\left(\text{Ω}\right)}^{\frac{2pq+4p-2q}{q+pq}}+c_7\\ \le \frac{p-1}{p}{\Vert {\left(u^{\frac{p}{2}}\right)}_x\Vert }_{L^2\left(\text{Ω}\right)}^2+c_8,\end{array}$ (3.10)

和

$\begin{array}{c}\text{Γ}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{q+2}{2}}v\text{d}x}\le \text{Γ}{\Vert v_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}{\displaystyle {\int }_{\text{Ω}}{u}^{\frac{q+2}{2}}\text{d}x}=\text{Γ}{\Vert v_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}{\Vert u^{\frac{p}{2}}\Vert }_{L^{\frac{q+2}{p}}\left(\text{Ω}\right)}^{\frac{q+2}{p}}\\ \le c_9{\Vert {\left(u^{\frac{p}{2}}\right)}_x\Vert }_{L^2\left(\text{Ω}\right)}^{\frac{q+2}{p}b}{\Vert u^{\frac{p}{2}}\Vert }_{L^{\frac{2}{p}}\left(\text{Ω}\right)}^{\frac{q+2}{p}\left(1-b\right)}+c_9{\Vert u^{\frac{p}{2}}\Vert }_{L^{\frac{2}{p}}\left(\text{Ω}\right)}^{\frac{q+2}{p}}\\ \le c_{10}{\Vert {\left(u^{\frac{p}{2}}\right)}_x\Vert }_{L^2\left(\text{Ω}\right)}^{\frac{pq}{p+p^2}}+c_{10}\\ \le \frac{p-1}{p}{\Vert {\left(u^{\frac{p}{2}}\right)}_x\Vert }_{L^2\left(\text{Ω}\right)}^2+c_{11},\end{array}$ (3.11)

其中 $a=\frac{p-\frac{q}{q+2}}{1+p}\in \left(0,1\right),b=\frac{p-\frac{2p}{q+2}}{1+p}\in \left(0,1\right),c_j>0\left(j=6,\cdots ,11\right)$ 。

将(3.10)，(3.11)代入(3.3)，并应用引理2.2，存在 $c_{12}>0$ ，有

$F+F^{\prime }\le c_{12},t\in \left(0,T_{\max }\right).$

应用常数变易法得到

$F\le \max \left\{c_{12},{\displaystyle {\int }_{\text{Ω}}{u}_0{}^p\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{v}_0{}^{-q+1}{v}_{0x}^q\text{d}x}\right\},t\in \left(0,T_{\max }\right).$

定理1.1 证明 由热半群表示，知

$u\left(\cdot ,t\right)={\text{e}}^{t\frac{{\partial }^2}{\partial x^2}}{u}_0-\text{χ}{\displaystyle {\int }_o^t{\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}{\left(\frac{u}{v^{\alpha }}{v}_x\right)}_x\text{d}s}+r{\displaystyle {\int }_o^t{\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}u\text{d}s}-\mu {\displaystyle {\int }_o^t{\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}{u}^k\text{d}s},$ (3.12)

$t\in \left(0,T_{\max }\right)$ 。利用文献 [6] 中Neumann热半群的 $L^P-L^q$ 估计，对 $p>1$ 有

$\begin{array}{l}{u}_{L^{\infty }\left(\text{Ω}\right)}\le {\Vert {\text{e}}^{t\frac{{\partial }^2}{\partial x^2}}{u}_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}+\chi {\displaystyle {\int }_o^t{\Vert {\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}{\left(\frac{u}{v^{\alpha }}{v}_x\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s}+\left|r\right|{\displaystyle {\int }_o^t{\Vert {\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}u\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s}\\ \le {\Vert u_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}+c_{13}{\displaystyle {\int }_o^t\left(1+{\left(t-s\right)}^{-\frac{3}{4}}\right){\text{e}}^{-\lambda \left(t-s\right)}{\Vert \frac{u}{v^{\alpha }}{v}_x\Vert }_{L^2\left(\text{Ω}\right)}\text{d}s}\\ +c_{13}{\displaystyle {\int }_o^t\left(1+{\left(t-s\right)}^{-\frac{1}{2p}}\right){\text{e}}^{-\lambda \left(t-s\right)}{\Vert u\Vert }_{L^p\left(\text{Ω}\right)}\text{d}s},t\in \left(0,T_{\max }\right),\end{array}$ (3.13)

其中 $c_{13}>0$ 。由引理3.4，有

${\displaystyle {\int }_{\text{Ω}}{u}^{4+\frac{1}{2\left(1-\alpha \right)}}\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{v}^{-\left(8+\frac{1}{\left(1-\alpha \right)}\right)+1}{\left|v_x\right|}^{8+\frac{1}{\left(1-\alpha \right)}}\text{d}x}\le c_{14},$

其中 $c_{14}>0$ 。进一步，利用Young不等式及(2.2)，存在 $c_{15}>0$ ，使得

$\begin{array}{c}{\displaystyle {\int }_{\text{Ω}}{\left(\frac{u}{v^{\alpha }}{v}_x\right)}^2\text{d}x}\le {\displaystyle {\int }_{\text{Ω}}{u}^4\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{\left|v^{-\alpha }{v}_x\right|}^4\text{d}x}\\ \le {\displaystyle {\int }_{\text{Ω}}{u}^{4+\frac{1}{2\left(1-\alpha \right)}}\text{d}x}+{\displaystyle {\int }_{\text{Ω}}{\left|v^{-\alpha }{v}_x\right|}^{8+\frac{1}{\left(1-\alpha \right)}}\text{d}x}+2\left|\text{Ω}\right|\\ \le {\displaystyle {\int }_{\text{Ω}}{u}^{4+\frac{1}{2\left(1-\alpha \right)}}\text{d}x}+2\left|\text{Ω}\right|\\ +{\Vert v_0\Vert }_{L^{\infty }\left(\text{Ω}\right)}^{8\left(1-\alpha \right)}{\displaystyle {\int }_{\text{Ω}}{v}^{-\left(8+\frac{1}{\left(1-\alpha \right)}\right)+1}{\left|v_x\right|}^{8+\frac{1}{\left(1-\alpha \right)}}\text{d}x}\\ \le c_{15},t\in \left(0,T_{\max }\right).\end{array}$ (3.14)

类似地，根据半群理论可以证得 ${\Vert v\Vert }_{W^{1,\infty }\left(\text{Ω}\right)}\le C_{\star }$ 。进而由引理2.1知 $T_{\max }=\infty$ 。

令 $w=v^{1-\beta }$ ， $\beta \in \left(0,1\right)$ 则

$w_t=\left(1-\beta \right)v^{-\beta }{v}_t=w_{xx}+\frac{\beta }{1-\beta }\frac{w_x^2}{w}-\left(1-\beta \right)wu,\forall t>0.$

通过热半群表示，知

$w\left(\cdot ,t\right)={\text{e}}^{t\frac{{\partial }^2}{\partial x^2}}{w}_0+\frac{\beta }{1-\beta }{\displaystyle {\int }_o^t{\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}\frac{w_x^2}{w}\text{d}s}-\left(1-\beta \right){\displaystyle {\int }_o^t{\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}wu\text{d}s},\forall t>0.$ (3.15)

应用Neumann热半群估计，对 $q>\max \left\{\frac{1}{1-\beta },\frac{2+\beta }{2}\right\}$ ，有

$\begin{array}{l}\left(1-\beta \right){\Vert \frac{v_x}{v^{\beta }}\Vert }_{L^{\infty }\left(\text{Ω}\right)}={\Vert w_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\\ \le {\Vert {\left({\text{e}}^{t\frac{{\partial }^2}{\partial x^2}}{w}_0\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}+\frac{\beta }{1-\beta }{\displaystyle {\int }_o^t{\Vert {\left({\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}\frac{w_x^2}{w}\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s}+\left(1-\beta \right){\displaystyle {\int }_o^t{\Vert {\left({\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}wu\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s}\\ ={\Vert {\left({\text{e}}^{t\frac{{\partial }^2}{\partial x^2}}{v}_0{}^{1-\beta }\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s+\beta \left(1-\beta \right){\displaystyle {\int }_o^t{\Vert {\left({\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}\frac{v_x^2}{v^{1+\beta }}\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s}+\left(1-\beta \right){\displaystyle {\int }_o^t{\Vert {\left({\text{e}}^{\left(t-s\right)\frac{{\partial }^2}{\partial x^2}}u{v}^{1-\beta }\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}\text{d}s}\\ \le {\Vert {\left(v_0{}^{1-\beta }\right)}_x\Vert }_{L^{\infty }\left(\text{Ω}\right)}+c_{16}{\displaystyle {\int }_o^t\left(1+{\left(t-s\right)}^{-\frac{1}{2}-\frac{1+\beta }{2\left(2q-1\right)}}\right){\text{e}}^{-\lambda \left(t-s\right)}{\Vert \frac{v_x^2}{v^{1+\beta }}\Vert }_{L^{\frac{2q-1}{1+\beta }}\left(\text{Ω}\right)}\text{d}s}\\ +c_{16}{\displaystyle {\int }_o^t\left(1+{\left(t-s\right)}^{-\frac{1}{2}-\frac{1}{2q}}\right){\text{e}}^{-\lambda \left(t-s\right)}{\Vert u{v}^{1-\beta }\Vert }_{L^q\left(\text{Ω}\right)}\text{d}s},\forall t>0,\end{array}$ (3.16)

其中 $c_{16}>0$ 。对(3.16)应用引理3.3及(2.2)，可得 ${\Vert \frac{v_x}{v^{\beta }}\Vert }_{L^{\infty }\left(\text{Ω}\right)}\le C_{\star },\forall t>0$ 。