Bergman空间上以拟齐次函数与径向函数的和函数为符号的Toeplitz算子的双正规性

Binormality of Toeplitz Operators with the Sum Function of Quasi-Homogeneous Function and Radial Function Symbols on the Bergman Space

摘要: 本文刻画了Bergman空间上以拟齐次函数与径向函数的和函数为符号的Toeplitz算子的双正规性。

Abstract: In this paper, we describe the binormality of Toeplitz operators with the sum of quasi-homogeneous function and radial function symbols on the Bergman space.

1. 引言

函数空间上的算子理论是泛函分析中一个较为活跃的分支。其中Toeplitz算子理论不仅与函数论、微分方程、Banach代数等数学学科中的问题相互关联、相互推动，并且在很多实际问题中有广泛应用。这使得Toeplitz算子一度成为学者们研究的热点且一直保持着很强的发展势态。正规性是Toeplitz算子的重要性质之一。迄今为止，Toeplitz算子的正规性已经得到了十分全面的刻画。于是人们将其推广拟正规性、双正规性和亚正规性。通过查阅资料发现，许多学者对于Bergman空间上以径向函数为符号的亚正规性得到了一些结果。Sumin [1] 丰富了Bergman空间上以径向函数为符号的Toeplitz算子的正规性的相关结论。Cuckovic [2] 研究了Bergman空间上以径向函数为符号的Toeplitz算子的正规性的充分必要条件。Lu和Shi [3] 进一步刻画了加权Bergman空间上以径向函数为符号的Toeplitz算子的亚正规性的充分必要条件。同样对于Bergman空间上以拟齐次函数为符号的亚正规性得到了一些结果。Lu和Liu [4] 刻画了加权Bergman空间上以拟齐次函数为符号的Toeplitz算子的亚正规的充分必要条件。但对于以拟齐次函数与径向函数的和函数为符号的Toeplitz算子的正规性、拟正规性、双正规性研究较少。本文的主要内容是Bergman空间上以拟齐次函数与径向函数的和函数为符号的Toeplitz算子的正规性、拟正规性、双正规性。

如果Hilbert空间上的有界线性算子S满足 $$ ，那么称算子S是正规的。如果Hilbert空间上的有界线性算子S满足 $S^{*}SS=S{S}^{*}S$ ，那么称算子S是拟正规的。如果Hilbert空间上的有界线性算子S满足 $S^{*}SS{S}^{*}=S{S}^{*}{S}^{*}S$ ，那么称算子S是双正规的。并且这些性质有如下关系：

正规性→拟正规性→双正规性

正规算子一定是拟正规算子，拟正规算子一定为双正规算子。

记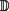为复平面上的开单位圆盘。Bergman空间 $A^2\left(\mathbb{D}\right)$ 中，对任意 $f,g\in A^2\left(\mathbb{D}\right)$ ，其上内积定义为

$\langle f,g\rangle ={\displaystyle {\int }_{\mathbb{D}}f\left(z\right)\overline{g\left(z\right)}\text{d}A\left(z\right)}.$

$L^{\infty }\left(\mathbb{D}\right)$ 是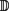上本性可测函数的空间。对于 $\phi \in L^{\infty }\left(\mathbb{D}\right)$ ，以 $\phi$ 为符号的Toeplitz算子 $T_{\phi }:A_{}^2\left(\mathbb{D}\right)\to A_{}^2\left(\mathbb{D}\right)$ 定义为

$T_{\phi }f=P\left(\phi f\right),f\in A_{}^2\left(\mathbb{D}\right).$

令P为 $L^2\left(\mathbb{D}\right)$ 到 $A^2\left(\mathbb{D}\right)$ 的正交投影。对任意 $f\in L^2\left(\mathbb{D}\right)$ 和 $z\in \mathbb{D}$ ，则有

$Pf\left(z\right)={\displaystyle {\int }_{\mathbb{D}}\frac{f\left(w\right)}{{\left(1-\bar{z}w\right)}^2}\text{d}A\left(w\right)}.$

2. 主要结论

引理2.1设 $\phi \in L^1\left(\left[0,1\right],rdr\right).$ 如果存在一个序列 $\left\{n_k\right\}\subset \mathbb{N}$ 满足

$\hat{\phi }\left(n_k\right)=0和{\displaystyle \underset{k=0}{\overset{\infty }{\sum }}\frac{1}{n_k}}=\infty ,$

那么，对于所有的 $z\in \left\{z:\mathrm{Re}z>2\right\}$ 有 $\hat{\phi }\left(z\right)=0$ ，于是有 $\phi \equiv 0$ 。

引理2.2在 $A^2\left(\mathbb{D}\right)$ 中，设 $a,b$ 为非负整数，

$P\left(z^a{\bar{z}}^b\right)=\{\begin{array}{l}\frac{a-b+1}{a+1}{z}^{a-b}\text{,}a\ge b\text{;}\\ 0\text{,}a<b.\end{array}$

引理2.3 [4] 在 $A_{\alpha }^2\left(\mathbb{D}\right)$ 中，令 $\phi \left(r{e}^{i\theta }\right)=e^{i\delta \theta }{\phi }_0\left(r\right)\in L^{\infty }\left(\mathbb{D}\right)$ ，其中 $\delta \in \mathbb{Z}$ ，

${\phi }_0\left(r\right)\in {\zeta }_a=\left\{a:\mathbb{D}\to ℂ|{\displaystyle {\int }_0^1{\left|a\left(r\right)\right|}^{2}r{\left(1-r^2\right)}^{\alpha }\text{d}r<\infty }\right\}$ 。则对于 $n\in {\mathbb{N}}_0$ ，有

$T_{\phi }{z}^n=\{\begin{array}{c}\frac{\left(2n+2\delta +2\right)\Gamma \left(n+\delta +2+\alpha \right)}{\left(n+\delta +1\right)!\Gamma \left(1+\alpha \right)}{\hat{\phi }}_{\alpha ,0}\left(2n+\delta +2\right)z^{n+\delta },n+\delta \ge 0,\\ 0,n+\delta <0.\end{array}$ $T_{\bar{\phi }}{z}^n=\{\begin{array}{c}\frac{\left(2n-2\delta +2\right)\Gamma \left(n-\delta +2+\alpha \right)}{\left(n-\delta +1\right)!\Gamma \left(1+\alpha \right)}{\hat{\phi }}_{\alpha ,0}\left(2n-\delta +2\right)z^{n-\delta },n-\delta \ge 0,\\ 0,n-\delta <0.\end{array}$

定理2.4设 $\varphi \left(r{e}^{i\theta }\right)=e^{i\delta \theta }\phi \left(r\right)+r^{2p}$ ，其中 $\delta \in \mathbb{N}$ ， $p\in \mathbb{N}$ 若 $T_{\varphi }$ 在 $A^2\left(\mathbb{D}\right)$ 是双正规算子当且仅当 $\phi \equiv 0$ 。

证明：第一种情况，考虑 $$ ，由Toeplitz算子的性质可知 $T_{\varphi }{z}^k=T_{{\phi }_1}{z}^k+T_{{\phi }_2}{z}^k$ ，其中 ${\phi }_1=e^{i\delta \theta }\phi \left(r\right)$ ， ${\phi }_2=r^{2p}$ 。

$\begin{array}{c}{T}_{{\phi }_2}{z}^k=P\left({\phi }_2{z}^k\right)\left(w\right)\\ ={\displaystyle \underset{\mathbb{D}}{\int }{\phi }_2\left(w\right)}{w}^k\frac{1}{{\left(1-z\bar{w}\right)}^2}\text{d}A\left(w\right)\\ \stackrel{w=r{e}^{i\theta }}{\text{=}}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\left(n+1\right)z^n}{\displaystyle {\int }_0^1{\displaystyle {\int }_0^{2\pi }{e}^{i\left(k-n\right)\theta }{r}^{2p+k+n}}}\frac{r}{\pi }\text{d}\theta \text{d}r\\ =\frac{k+1}{p+k+1}{z}^k\left(k\ge 0\right),\end{array}$

由引理2.3知

$T_{{\phi }_1}{z}^k=\{\begin{array}{c}2\left(k+\delta +1\right)\hat{\phi }\left(2k+\delta +2\right)z^{k+\delta },k+\delta \ge 0\\ 0,k+\delta <0\end{array},$

故

$T_{\varphi }{z}^k=\{\begin{array}{c}2\left(k+\delta +1\right)\hat{\phi }\left(2k+\delta +2\right)z^{k+\delta }+\frac{k+1}{p+k+1}{z}^k,k+\delta \ge 0\\ \frac{k+1}{p+k+1}{z}^k,k+\delta <0\end{array}.$

同理可得

$T_{{\bar{\phi }}_2}{z}^k=\frac{k+1}{p+k+1}{z}^k\left(k\ge 0\right),$

再由引理2.3知

$T_{{\bar{\phi }}_1}{z}^k=\{\begin{array}{c}2\left(k-\delta +1\right)\hat{\phi }\left(2k-\delta +2\right)z^{k-\delta },k-\delta \ge 0\\ 0,k-\delta <0\end{array},$

故

$T_{\bar{\varphi }}{z}^k=\{\begin{array}{c}2\left(k-\delta +1\right)\hat{\phi }\left(2k-\delta +2\right)z^{k-\delta }+\frac{k+1}{p+k+1}{z}^k,k-\delta \ge 0\\ \frac{k+1}{p+k+1}{z}^k,k-\delta <0\end{array}.$

当 $0\le k<\delta$ ，

$T_{\varphi }{T}_{\varphi }^{\ast }{z}^k\text{=}\frac{k+1}{p+k+1}{T}_{\varphi }{z}^k=\frac{{\left(k+1\right)}^2}{{\left(p+k+1\right)}^2}{z}^k+\frac{2\left(k+\delta +1\right)\left(k+1\right)}{p+k+1}\hat{\phi }\left(2k+\delta +2\right)z^{k+\delta }.$

进而

$\begin{array}{c}{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k\\ \text{=}[\frac{2{\left(k+\delta +1\right)}^2\left(k+1\right)}{\left(p+k+\delta +1\right)\left(p+k+1\right)}\hat{\phi }\left(2k+\delta +2\right)+\frac{2{\left(k+1\right)}^2\left(k+\delta +1\right)}{{\left(p+k+1\right)}^2}\hat{\phi }\left(2k+\delta +2\right)]z^{k+\delta }\\ \begin{array}{cc}& \end{array}+\frac{4\left(k+\delta +1\right)\left(k+1\right)\left(k+2\delta +1\right)}{p+k+1}\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)z^{k+2\delta }\\ \begin{array}{ccc}& & \end{array}+\frac{{\left(k+1\right)}^3}{{\left(p+k+1\right)}^3}{z}^k.\end{array}$

再由直接计算得到

$\begin{array}{c}{T}_{\varphi }^{\ast }{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k\\ \text{=}[\frac{8{\left(k+\delta +1\right)}^2\left(k+1\right)\left(k+2\delta +1\right)}{p+k+1}\hat{\phi }\left(2k+\delta +2\right){\left|\hat{\phi }\left(2k+3\delta +2\right)\right|}^2\\ \begin{array}{cc}& \end{array}+\frac{2{\left(k+1\right)}^2{\left(k+\delta +1\right)}^2}{{\left(p+k+1\right)}^2\left(p+k+\delta +1\right)}\hat{\phi }\left(2k+\delta +2\right)+\frac{2{\left(k+\delta +1\right)}^3\left(k+1\right)}{{\left(p+k+\delta +1\right)}^2\left(p+k+1\right)}\hat{\phi }\left(2k+\delta +2\right)]z^{k+\delta }\\ \begin{array}{ccc}& & \end{array}+\frac{4\left(k+\delta +1\right)\left(k+1\right){\left(k+2\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k+2\delta +1\right)}\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)z^{k+2\delta }\\ \begin{array}{cccc}& & & \end{array}+[\frac{4{\left(k+1\right)}^3\left(k+\delta +1\right)}{{\left(p+k+1\right)}^2}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^4}{{\left(p+k+1\right)}^4}\\ \begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & \end{array}+\frac{4{\left(k+1\right)}^2{\left(k+\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k+\delta +1\right)}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2]z^k.\end{array}$

另一方面

$\begin{array}{c}{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k\\ =\left[4\left(k+1\right)\left(k+\delta +1\right){\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^2}{{\left(p+k+1\right)}^2}\right]z^k+\frac{2{\left(k+\delta +1\right)}^2}{p+k+\delta +1}\hat{\phi }\left(2k+\delta +2\right)z^{k+\delta }.\end{array}$

进而

$\begin{array}{l}{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k\\ \text{=}\left[\frac{4{\left(k+1\right)}^2\left(k+\delta +1\right)}{p+k+1}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2+\frac{4\left(k+1\right){\left(k+\delta +1\right)}^2}{p+k+\delta +1}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^3}{{\left(p+k+1\right)}^3}\right]z^k\\ \begin{array}{cc}& \end{array}+\frac{2{\left(k+\delta +1\right)}^3}{{\left(p+k+\delta +1\right)}^2}\hat{\phi }\left(2k+\delta +2\right)z^{k+\delta }.\end{array}$

再由直接计算得到

$\begin{array}{c}{T}_{\varphi }{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k\\ \text{=}[\frac{8{\left(k+1\right)}^2{\left(k+\delta +1\right)}^2}{p+k+1}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^3+\frac{8{\left(k+\delta +1\right)}^3\left(k+1\right)}{p+k+\delta +1}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^3\\ \begin{array}{cc}& \end{array}+\frac{2{\left(k+1\right)}^3\left(k+\delta +1\right)}{{\left(p+k+1\right)}^3}\hat{\phi }\left(2k+\delta +2\right)+\frac{2{\left(k+\delta +1\right)}^4}{{\left(p+k+\delta +1\right)}^3}\hat{\phi }\left(2k+\delta +2\right)]z^{k+\delta }\\ \begin{array}{ccc}& & \end{array}+\frac{4{\left(k+\delta +1\right)}^3\left(k+2\delta +1\right)}{{\left(p+k+\delta +1\right)}^2}\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)z^{k+2\delta }\\ \begin{array}{cccc}& & & \end{array}+[\frac{4{\left(k+1\right)}^3\left(k+\delta +1\right)}{{\left(p+k+1\right)}^2}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^4}{{\left(p+k+1\right)}^4}\\ \begin{array}{cccc}\begin{array}{cc}& \end{array}& & & \end{array}+\frac{4{\left(k+1\right)}^2{\left(k+\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k+\delta +1\right)}{\left|\hat{\phi }\left(2k+\delta +2\right)\right|}^2]z^k.\end{array}$

当 $0\le k<\delta$ 时， $T_{\varphi }$ 在 $A^2\left(\mathbb{D}\right)$ 是双正规算子则有 $T_{\varphi }^{\ast }{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }=T_{\varphi }{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }$ ，那么有 $T_{\varphi }^{\ast }{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k=T_{\varphi }{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k$ ，

对比 $z^{k+2\delta }$ 的系数可知：

$\begin{array}{l}\frac{4\left(k+\delta +1\right)\left(k+1\right){\left(k+2\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k+2\delta +1\right)}\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)\\ =\frac{4{\left(k+\delta +1\right)}^3\left(k+2\delta +1\right)}{{\left(p+k+\delta +1\right)}^2}\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)\end{array}$

即

$\begin{array}{l}4\left(k+\delta +1\right)\left(k+2\delta +1\right)\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \times \end{array}\left[\frac{{\left(k+\delta +1\right)}^2}{{\left(p+k+\delta +1\right)}^2}-\frac{\left(k+1\right)\left(k+2\delta +1\right)}{\left(p+k+1\right)\left(p+k+2\delta +1\right)}\right]=0\end{array}$

但当 $0\le k<\delta$ ，若

$\begin{array}{l}\frac{{\left(k+\delta +1\right)}^2}{{\left(p+k+\delta +1\right)}^2}-\frac{\left(k+1\right)\left(k+2\delta +1\right)}{\left(p+k+1\right)\left(p+k+2\delta +1\right)}\\ =\frac{{\delta }^{2}p\left[2\left(k+1\right)+p+2\delta \right]}{{\left(p+k+\delta +1\right)}^2\left(p+k+1\right)\left(p+k+2\delta +1\right)}=0,\end{array}$

则 $k=-\frac{p}{2}-\delta -1<0$ ，矛盾。所以有 $\hat{\phi }\left(2k+\delta +2\right)\hat{\phi }\left(2k+3\delta +2\right)=0$ 。

若 $\hat{\phi }\left(2k+\delta +2\right)=0$ ，则等式成立。若 $\hat{\phi }\left(2k+\delta +2\right)\ne 0,\hat{\phi }\left(2k+3\delta +2\right)=0$ ，则 $z^{k+\delta }$ 的系数不相等。故当 $0\le k<\delta$ ，有 $\hat{\phi }\left(2k+\delta +2\right)=0$ ，根据引理2得到 $\phi =0$ 。

第二种情况，考虑 $\delta <0$ ，当 $0\le k<-\delta$ ，

$\begin{array}{c}{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k\\ =\left[4\left(k+1\right)\left(k-\delta +1\right){\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^2}{{\left(p+k+1\right)}^2}\right]z^k+\frac{2{\left(k-\delta +1\right)}^2}{p+k-\delta +1}\hat{\phi }\left(2k-\delta +2\right)z^{k-\delta }.\end{array}$

进而

$\begin{array}{l}{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k\\ \text{=}\left[\frac{4{\left(k+1\right)}^2\left(k-\delta +1\right)}{p+k-\delta +1}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2+\frac{4\left(k+1\right){\left(k-\delta +1\right)}^2}{p+k+1}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^3}{{\left(p+k+1\right)}^3}\right]z^k\\ \begin{array}{cc}& \end{array}+\frac{2{\left(k-\delta +1\right)}^3}{{\left(p+k-\delta +1\right)}^2}\hat{\phi }\left(2k-\delta +2\right)z^{k-\delta }.\end{array}$

再由直接计算得到

$\begin{array}{c}{T}_{\varphi }^{\ast }{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k\\ \text{=}[\frac{8{\left(k+1\right)}^2{\left(k-\delta +1\right)}^2}{p+k+1}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^3+\frac{8{\left(k-\delta +1\right)}^3\left(k+1\right)}{p+k-\delta +1}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^3\\ \begin{array}{cc}& \end{array}+\frac{2{\left(k+1\right)}^3\left(k-\delta +1\right)}{{\left(p+k+1\right)}^3}\hat{\phi }\left(2k-\delta +2\right)+\frac{2{\left(k-\delta +1\right)}^4}{{\left(p+k-\delta +1\right)}^3}\hat{\phi }\left(2k-\delta +2\right)]z^{k-\delta }\\ \begin{array}{ccc}& & \end{array}+\frac{4{\left(k-\delta +1\right)}^3\left(k-2\delta +1\right)}{{\left(p+k-\delta +1\right)}^2}\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)z^{k-2\delta }\\ \begin{array}{cccc}& & & \end{array}+[\frac{4{\left(k+1\right)}^3\left(k-\delta +1\right)}{{\left(p+k+1\right)}^2}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^4}{{\left(p+k+1\right)}^4}\\ \begin{array}{cccc}\begin{array}{cc}& \end{array}& & & \end{array}+\frac{4{\left(k+1\right)}^2{\left(k-\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k-\delta +1\right)}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2]z^k.\end{array}$

另一方面

$T_{\varphi }^{\ast }{T}_{\varphi }{z}^k\text{=}\frac{k+1}{p+k+1}{T}_{\varphi }^{\ast }{z}^k=\frac{{\left(k+1\right)}^2}{{\left(p+k+1\right)}^2}{z}^k+\frac{2\left(k-\delta +1\right)\left(k+1\right)}{p+k+1}\hat{\phi }\left(2k-\delta +2\right)z^{k-\delta }.$

进而

$\begin{array}{c}{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k\text{=}[\frac{2{\left(k-\delta +1\right)}^2\left(k+1\right)}{\left(p+k-\delta +1\right)\left(p+k+1\right)}\hat{\phi }\left(2k-\delta +2\right)+\frac{2{\left(k+1\right)}^2\left(k-\delta +1\right)}{{\left(p+k+1\right)}^2}\hat{\phi }\left(2k-\delta +2\right)]z^{k-\delta }\\ +\frac{4\left(k-\delta +1\right)\left(k+1\right)\left(k-2\delta +1\right)}{p+k+1}\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)z^{k-2\delta }+\frac{{\left(k+1\right)}^3}{{\left(p+k+1\right)}^3}{z}^k.\end{array}$

再由直接计算得到

$\begin{array}{c}{T}_{\varphi }{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k\\ \text{=}[\frac{8{\left(k-\delta +1\right)}^2\left(k+1\right)\left(k-2\delta +1\right)}{p+k+1}\hat{\phi }\left(2k-\delta +2\right){\left|\hat{\phi }\left(2k-3\delta +2\right)\right|}^2\\ \begin{array}{cc}& \end{array}+\frac{2{\left(k+1\right)}^2{\left(k-\delta +1\right)}^2}{{\left(p+k+1\right)}^2\left(p+k-\delta +1\right)}\hat{\phi }\left(2k-\delta +2\right)+\frac{2{\left(k-\delta +1\right)}^3\left(k+1\right)}{{\left(p+k-\delta +1\right)}^2\left(p+k+1\right)}\hat{\phi }\left(2k-\delta +2\right)]z^{k-\delta }\\ \begin{array}{ccc}& & \end{array}+\frac{4\left(k-\delta +1\right)\left(k+1\right){\left(k-2\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k-2\delta +1\right)}\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)z^{k-2\delta }\\ \begin{array}{cccc}& & & \end{array}+[\frac{4{\left(k+1\right)}^3\left(k-\delta +1\right)}{{\left(p+k+1\right)}^2}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2+\frac{{\left(k+1\right)}^4}{{\left(p+k+1\right)}^4}\\ \begin{array}{ccc}\begin{array}{cc}\begin{array}{cc}& \end{array}& \end{array}& & \end{array}+\frac{4{\left(k+1\right)}^2{\left(k-\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k-\delta +1\right)}{\left|\hat{\phi }\left(2k-\delta +2\right)\right|}^2]z^k.\end{array}$

当 $0\le k<-\delta$ 时， $T_{\varphi }$ 在 $A^2\left(\mathbb{D}\right)$ 是双正规算子则有 $T_{\varphi }^{\ast }{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }=T_{\varphi }{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }$ ，那么有 $T_{\varphi }^{\ast }{T}_{\varphi }{T}_{\varphi }{T}_{\varphi }^{\ast }{z}^k=T_{\varphi }{T}_{\varphi }^{\ast }{T}_{\varphi }^{\ast }{T}_{\varphi }{z}^k$ ，

对比 $z^{k-2\delta }$ 的系数可知：

$\begin{array}{l}\frac{4\left(k-\delta +1\right)\left(k+1\right){\left(k-2\delta +1\right)}^2}{\left(p+k+1\right)\left(p+k-2\delta +1\right)}\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)\\ =\frac{4{\left(k-\delta +1\right)}^3\left(k-2\delta +1\right)}{{\left(p+k-\delta +1\right)}^2}\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)\end{array}$

即

$\begin{array}{l}4\left(k-\delta +1\right)\left(k-2\delta +1\right)\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)\\ \begin{array}{cc}\begin{array}{cc}& \end{array}& \times \end{array}\left[\frac{{\left(k-\delta +1\right)}^2}{{\left(p+k-\delta +1\right)}^2}-\frac{\left(k+1\right)\left(k-2\delta +1\right)}{\left(p+k+1\right)\left(p+k-2\delta +1\right)}\right]=0\end{array}$

但当 $0\le k<-\delta$ ，若

$\begin{array}{l}\frac{{\left(k-\delta +1\right)}^2}{{\left(p+k-\delta +1\right)}^2}-\frac{\left(k+1\right)\left(k-2\delta +1\right)}{\left(p+k+1\right)\left(p+k-2\delta +1\right)}\\ =\frac{{\delta }^{2}p\left[2\left(k+1\right)+p-2\delta \right]}{{\left(p+k-\delta +1\right)}^2\left(p+k+1\right)\left(p+k-2\delta +1\right)}=0,\end{array}$

则 $k=-\frac{p}{2}+\delta -1<0$ ，矛盾。所以有 $\hat{\phi }\left(2k-\delta +2\right)\hat{\phi }\left(2k-3\delta +2\right)=0$ 。

若 $\hat{\phi }\left(2k-\delta +2\right)=0$ ，对比各项系数相等，则 $T_{\varphi }$ 是双正规算子。若 $\hat{\phi }\left(2k-\delta +2\right)\ne 0,\hat{\phi }\left(2k-3\delta +2\right)=0$ ，则 $z^{k-\delta }$ 的系数不相等。故当 $0\le k<-\delta$ ，有 $\hat{\phi }\left(2k-\delta +2\right)=0$ ，根据引理1得到 $\phi =0$ 。

充分性显然，当 $\phi =0$ ， $\varphi \left(r{e}^{i\theta }\right)=r^{2p}$ ， $T_{\varphi }$ 是双正规算子，定理得证。

显而易见，正规算子蕴含拟正规算子，拟正规算子蕴含双正规算子，因此根据定理2.4还可以得到以下推论。

推论2.5设 $\varphi \left(r{e}^{i\theta }\right)=e^{i\delta \theta }\phi \left(r\right)+r^{2p}$ ，其中 $\delta \in \mathbb{N}$ ， $p\in \mathbb{N}$ 。若 $T_{\varphi }$ 在 $A^2\left(\mathbb{D}\right)$ 是双正规算子当且仅当 $T_{\varphi }$ 在 $A^2\left(\mathbb{D}\right)$ 是正规算子当且仅当 $T_{\varphi }$ 在 $A^2\left(\mathbb{D}\right)$ 是拟正规算子。

证明：由定理2.4可知。

本文研究了Bergman空间上以径向函数与拟齐次函数的和函数为符号的Toeplitz算子的双正规性的充分必要条件。