1. 引言
数据科学中的许多问题(例如,机器学习,优化和统计)可以被描述为这种形式的损失最小化问题:
(1)
其中:
(2)
这里n为样本量,每个
为第i个样本数据对应的损失函数。在本文中,我们假设每个分量函数
都是凸函数且可微,并且函数
是强凸的。
问题(1)当n非常大时是极具挑战性的。由于精确的全梯度信息不易获得,因此基于精确梯度的方法不切实际且被禁止。然而,随机梯度下降法(SGD)可以追溯到 [1] 的开创性工作,已经成为解决问题(1)的主要方法。在第n次迭代中,SGD随机选取索引
,然后更新迭代
通过:
(3)
其中
为步长(也称为学习率),
表示
处的样本梯度。在(3)中,通常假设
是对
的无偏估计,即:
(4)
然而,已知SGD的梯度评估的总次数取决于随机梯度的方差,并且对于强凸光滑问题(1)具有次线性收敛速率。为了提升SGD方法的性能,人们后续提出了许多改进方法。其中包括梯度聚合算法 [2] ,如SAG [3] [4] 和SAGA [5] 。他们将随机梯度计算为在之前迭代中评估的随机梯度的平均值。然后它们以牺牲内存为代价来存储之前的随机梯度。 [3] 表明SAG对于强凸问题是线性收敛的。Defazio等 [5] 提出的SAGA方法是SAG的改进版本,它不需要强凸性假设。SVRG [6] 有两个循环,外层循环计算一个完整的梯度,内层循环计算方差较小的随机梯度。S2GD [7] 在每个历元中运行随机数的随机梯度,遵循几何规律。Batching SVRG [8] 选择一个大的批样集来近似每个外环的全梯度。上述算法中的梯度估计量是无偏的。随机梯度递归算法(SARAH) [9] 采用一种简单的递归框架来更新随机梯度估计。SARAH算法结合了现有算法的一些优点,如SAGA和SVRG,同时旨在改进这两种方法。特别是,SARAH算法没有沿着随机梯度方向更新,而是沿着使用过去的随机梯度信息(如SAGA)和偶尔的精确梯度信息(如SVRG)的累积方向更新。SARAH算法和SVRG算法基本相似,其不同的地方就在于在内循环。两者更新方式的差别如下所示:
SARAH算法的关键步骤是随机梯度估计的递归更新(SARAH更新)。
(5)
其迭代更新为:
(6)
SVRG更新则是:
(7)
近年来,Barzilai-Borwein (BB)方法越来越受到学者的关注。许多与BB算法相关的算法已经被提出。Tan等 [10] 提出了SGD-BB和SVRG-BB方法。Liu等 [11] 把重要抽样策略引入到SARAH方法中得到了SARAH-I算法,计算每个内循环最后一次迭代的全梯度。并且将BB算法与SARAH-I算法结合,得到了SARAH-I-BB算法。
BB方法在求解非线性优化问题方面非常成功。BB方法背后的关键思想是由拟牛顿方法激发的。假设我们要解决无约束最小化问题为:
(8)
其中f是可微的。求解(8)的拟牛顿方法的典型迭代形式如下:
(9)
其中
是f在当前迭代
下的Hessian矩阵的近似值。
最重要的特征是它必须满足割线方程:
(10)
BB步长满足最小二乘意义上的某些正割方程,引入了以下长、短选择:
(11)
以及
(12)
其中
、
和
。BB步长在二维严格凸二次型中带来了惊人的R超线性收敛。Raydan [12] 通过配合Grippo等人 [13] 的非单调直线搜索,首先将BB方法扩展到无约束优化,得到了一种非常高效的梯度方法GBB。Birgin等 [14] 进一步扩展了BB法求解约束优化问题。Yuan [15] [16] 建议计算步长,使前一步和后一步使用SD步长,从而在三次迭代中实现二维严格凸二次函数的最小化。Dai和Yuan [17] 通过修改Yuan的步长,适当地与SD步长交替,提出了所谓的Dai-Yuan (单调)梯度法,其性能甚至优于(非单调) BB法。
Huang等人 [18] 通过自适应地采用长BB步和与新步长相关的短步长结合,开发了一种有效的梯度方法,用于二次优化,使梯度法实现二维二次终止。本文将该步长与SARAH-I算法相结合,使其数值效果得到不错的提升。
本文的主要贡献如下:
在本文中,我们提出了一种新的算法,在SARAH算法中引入了能够自适应计算的步长。采用固定步长的SARAH算法对于初始步长的选取非常敏感,而新算法对于初始步长的选取并不敏感。此外,我们给出了新提出算法在强凸条件下的线性收敛性证明。数值结果证明了新算法的有效性,并表明该算法与在最佳步长调整情况下的SARAH-I算法数值性能相当。
本文的其余部分组织如下。在第2节中,我们提出了新的随机递归梯度算法。在第3节中,我们针对提出的算法,证明了它对强凸函数的线性收敛性。第4节中我们针对提出的算法进行了数值实验。最后,我们在第5节中得出了一些结论。
2. 新算法的提出
原始SARAH [8] 方法通过内环中与之前的
的分量梯度加减,递归地更新随机梯度步长
。SARAH-I算法考虑一般分布
的随机抽样,这比SARAH中原来的均匀抽样方案更灵活。SARAH-I算法伪代码如下表算法1所示。
步骤6表示的是随机抽样的方案。在
和
的条件下,我们得到了
关于
的期望:
(13)
因为
是
的无偏估计。在步骤10中,将
设置为内部迭代的最后一次迭代,这是SARAH-I与原始SARAH [8] 最重要的区别。这似乎是更合理的选择,因为使用了每个内循环中的最新信息。
Huang等人 [18] 提出的步长由下面给出。
(14)
其中:
以及
下面的定理分别给出了步长(14)在
,
时与
,
两种情况下的界,具体证明过程参见 [18] 。
定理1 [18] :由(14)式给出的步长是良定的,并且当
与
时有:
(15)
当
及
,有
(16)
大量研究表明,采用长BB步长
(因为
)和一些短步长交替或自适应的方法在数值上优于原始BB方法。如果
和
,由定理1可以知道,步长
小于
和
两个短步长。另一方面,当
和
时,步长
都大于
和
两个步长。结合这两种情况,将
进行替换,替换为
,替换后的步长为
、
、及
中最大的一个。
由于自适应方案的成功,Huang等人 [18] 在其基础上提出步长的截断形式如下:
(17)
其中
。更新(17)中的
的最简单方法是将对所有k都设置为某个常数
。对于这种固定格式,步长(17)的性能可能在很大程度上取决于τ的值。另一个策略是动态地更新
,更新方式如下:
(18)
显然,固定格式的τ是(18)中
的一种特殊情况。
本文基于上述思想的提出,将SARAH-I算法和如(17)形式的BB类步长相结合。使原本采用固定步长的SARAH-I算法装备上能够自适应计算的步长(17)。
SARAH-I算法引入了重要抽样原则,计算每个内循环最后一次迭代的全梯度。在求解强凸问题(1)时,Liu等人 [11] 证明了非强凸优化SARAH-I的线性收敛性。在严格割线不等式下,证明了迭代到最优集的距离期望是线性收敛的。
Huang等人 [18] 引入的步长
如(17)所示。使得BB方法在加入
后具有二维二次终止性。这种新颖的步长只利用了之前迭代的BB步长,因此可以很容易地用于一般的无约束和有约束优化。将步长(17)应用在SARAH-I算法中是非常具有潜力的。在后续的数值实验中我们可以发现新算法具有能够自动生成SARAH-I算法中最佳步长的能力,并且对于初始步长的选取很不敏感。
下面,我们提出新的算法方法,采用(17)式自适应计算步长。我们现在在下面的算法2中描述它的框架。
3. 收敛性分析
为了验证新算法的收敛性。我们先引入SARAH-I算法在强凸条件下的收敛性结果。在此之前先引入如下的假设。
假设1:每个分量函数
,是凸的且一阶连续可微的。以及每个分量函数
的梯度是L-Lipschitz连续的,即:对任意的
有:
在此假设下,不难看出
也是L-Lipschitz连续的。为简单起见,我们将
表示为:
引理1是假设1成立下的结果。
引理1:假设f是凸函数以及
是L-Lipschitz连续的。则对任意的
有:
现在给出SARAH-I算法的收敛性结果。
定理2 [11] :假定假设1成立以及
。如果f是μ强凸的,则对于任意的
,当
有:
因此,如果m和a的选择使得
,则那么SARAH-I算法以期望线性收敛,即:
下面的定理表明,只要内部迭代次数m足够大,算法2具有线性收敛速率。假定
是由算法2产生的序列。
定理3:假定假设1成立以及f是μ强凸的。给定
,如果m的选择使得
,则对于任意的
有:
证明:由步长(17)的形式可以很容易得出
。由
的Lipschitz连续性可以得出:
同时由f的强凸性可以得到
因此,定理3中的系数
有下界:
这就完成了我们的证明。
4. 数值实验
在本节中,我们进行了大量的实验来证明我们提出的算法的优势。我们分别在LIBSVM1网站上公开提供的3个不同的训练数据集上评估了我们的算法。这些数据集的详细信息如表1所示。注意,这五列分别表示数据集的名称、数据集的大小、特征的维度、应用的模型、正则化方法的系数。其中LR表示logistic回归,SVM表示带有
范数正则化的平方铰链损失支持向量机。为了公平起见所有的数值实验都是在一台CPU为i5-7300HQ的笔记本电脑上,在MATLAB 8.4中实现的。

Table 1. Data and model information of the experiments
表1. 实验数据和模型信息
新算法解决的两个问题如下:
带有
范数正则化的逻辑回归(LR):
(19)
和带有
范数正则化的平方铰链损失支持向量机(SVM):
(20)
下面我们给出算法2和SARAH-I算法在不同步长(对于算法SARAH-I)和不同初始步长(对于算法2)下的次优性
比较。这里我们设置内循环大小
。
在图1~3中,横坐标代表的是迭代次数,纵坐标代表的是次优性:
。
红色的虚线对应于每个图中具有最佳调优固定步长的SARAH-I,黄色虚线代表较最调优步长稍小的步长,蓝色虚线代表较最调优步长稍大的步长。带*号的实线就是我们算法2的数值效果。观察图1~3,我们可以看到SARAH-I算法对于三种不同大小步长的选取,其数值效果差别很大。但是算法2对于三种不同大小初始步长的选取,其数值效果非常接近。所以算法2对初始步长的选择不敏感。

Figure 1. Sub-optimality comparison on w8a
图1. w8a上的次优性比较

Figure 2. Sub-optimality comparison on a9a
图2. a9a上的次优性比较
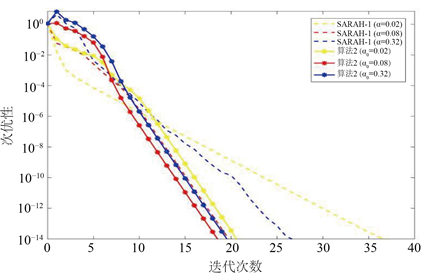
Figure 3. Sub-optimality comparison on ijcnn1
图3. ijcnn1上的次优性比较

Figure 6. Stepsizes variation on ijcnn1
图6. ijcnn1上的步长变化
在图4~6中,横坐标代表的是迭代次数,纵坐标代表的是步长变化。其中三条虚线表示的是取不同固定步长下的SARAH-I算法。红色虚线表示最调优步长,黄色虚线是比最调优步长小的步长,蓝色虚线是比最调优步长大的步长。三条实线则表示不同初始步长下的算法2中的步长变化。从图4~6可以看出算法2中产生的步长最终将接近于SARAH-I算法中的最调优步长。因此新算法具有能自动生成最优步长的能力。
5. 结论
本文通过对SARAH-I算法采取自适应学习率的策略,引入了一种具有二维二次终止性的BB类步长。该步长自适应地采用长BB步和与该步长相关的短步长结合,具有较好的数值性能。并且我们在强凸条件下证明了算法2的线性收敛性。对于提出的新算法,我们在3个不同的训练数据集上进行了数值实验。实验结果发现,新算法能够达到与最具调优步长的SARAH-I算法相同的次优性程度,并且新算法对于初始步长的选取是非常不敏感的,而采用固定步长的SARAH-I算法对于不同步长的选取所得出的数值性能差异太大。最后通过对步长变化的观察,我们发现在算法2中产生的步长最终将接近于SARAH-I算法中的最调优步长。因此算法2具有能自动生成最优步长的能力,我们有理由相信新算法是鲁棒的。
NOTES
1http://www.csie.ntu.edu.tw/~cjlin/libsvmtools/datasets/