某汽车空气弹簧的疲劳寿命分析

Fatigue Life Analysis of an Automobile Air Spring

摘要: 建立空气弹簧的实体模型，并通过几何处理、网格划分、属性赋予等操作创建了空气弹簧的有限元模型，之后在Abaqus软件中对空气弹簧设置与实际相符合的边界条件，并选取其最大垂向位移工况进行静力学分析，通过静力学分析结果获得空气弹簧垂向的应力与应变的数据，对应力、应变数据进行整理并通过Origin软件进行绘图，得到其静刚度特性曲线。基于有限元仿真结果，在Fe-safe软件中结合软件自带的橡胶材料库，运用以开裂能理论为原理的疲劳分析方法对空气弹簧气囊进行疲劳寿命评估。分析求解结果中空气弹簧最容易受到破坏的位置，对空气弹簧的合理设计具有一定的指导意义。

Abstract: The solid model of the air spring was established, and the finite element model of the air spring was created through geometric processing, meshing, attribute assignment and other operations, and then the boundary conditions of the air spring were set in the Abaqus software that matched the actual situation, and its maximum vertical displacement working condition was selected for static analysis. The strain data is collated and plotted by Origin software to obtain its static stiffness char-acteristic curve. Based on the finite element simulation results, the fatigue life of the air spring bladder was evaluated by using the fatigue analysis method based on the cracking energy theory in Fe-safe software combined with the rubber material library included in the software. The position of the gas spring that is most susceptible to damage in the analysis and solution results has a certain guiding significance for the reasonable design of the air spring.

1. 引言

悬架系统减振元件的优劣性对于行驶车辆平顺性和操纵稳定性具有直接影响，而空气弹簧作为一种低频减振器，具有可变刚度、高度可控、隔振效果好等优点 [1] 。空气弹簧的工作原理是一种利用橡胶气囊内部压缩空气的反力作为弹性恢复力的弹性元件 [2] 。空气弹簧在类型上大致可以分为三种：膜式空气弹簧、囊式空气弹簧和袖筒式空气弹簧，由于膜式弹簧的刚度相较于囊式弹簧小，且结构简单，通过改变结构即可获得理想的弹性特性，因此在乘用车上普遍采用该类空气弹簧 [3] ，本文所研究对象也为某汽车上的膜式空气弹簧。

在实际行驶过程中，由于工作环境变化较大且路面情况复杂，空气弹簧在承受车身带来的垂向载荷之外还需要承受路面不平整带来的交变载荷。在交变载荷的作用下，易引起空气弹簧疲劳破坏，直接影响空气弹簧的使用寿命，因此空气弹簧在刚度，疲劳及可靠性方面都有很高的要求。因此对空气弹簧进行刚度分析及疲劳寿命评估，对提高汽车行驶安全性，降低空气弹簧的开发成本具有重要意义。

国内对于空气弹簧寿命的研究起步较晚，丁智平等 [4] 基于断裂力学、开裂能理论，通过FCG试验，将最大撕裂能量范围作为疲劳损伤参量，应用等效应力法以单轴疲劳试验数据预测多轴橡胶弹簧的疲劳寿命。李志超等 [5] 基于开裂能量密度(CED)理论对空气弹簧橡胶支座进行疲劳分析并进行结构优化。陈涛等 [6] 使用热空气加速老化法对轨道车辆一系橡胶弹簧进行定载荷尺寸保持率的失效寿命预测。

但由于通过真实试验等方式对空气弹簧进行刚度以及疲劳寿命预测的成本较大，而虚拟疲劳试验相对真实试验具有试验周期短、试验成本较低等优点 [7] ，因此基于开裂能理论，本文提出了一种虚拟疲劳仿真试验的空气弹簧的寿命预测方法，期望可以对空气弹簧的寿命预测提供一些方法。

2. 空气弹簧模型建立

2.1. 空气弹簧各部件三维数模的创建

本文在Abaqus中对选取的目标车辆的空气弹簧进行三维建模，所建立的三维模型一共分为三部分：上盖板、橡胶气囊、活塞。对于活塞与上盖板的疲劳极限远远大于橡胶气囊的疲劳极限，在弹簧工作期间，其几乎没有形变，因此为了简化模型，节约算力，将上盖板与活塞在Abaqus中因此采用3维可变形实体(Rigid)单元进行模拟，同时设置相应的参考点，之后的载荷设置可以直接设定在参考点上。对于空气弹簧，由于气囊内部有帘线层，所以在建模时选用3维可变形壳体(Shell)单元。所建立的三维数模如下图1所示，图中1为上盖板、2为橡胶气囊、3为活塞。

Figure 1. Schematic diagram of the three-dimensional model of the gas spring

图1. 空气弹簧三维模型示意图

2.2. 三维模型材料本构模型的选取以及参数设置

空气弹簧中气囊橡胶是典型的超弹性材料，具有明显的材料非线性特性，要准确地表征其本构关系，需要采用应变能密度函数来描述。本文只考虑橡胶的非线性，且假设材料的不可压缩性，因此其力学性能可用Mooney-Rivlin模型来描述 [8]

$U=C_{10}\left(I_1-3\right)+C_{01}\left(I_2-3\right)$ (1)

式中：U为应变能密度函数，C₁₀、C₀₁为超弹性材料常数，I₁、I₂分别为第1和第2偏应变量。根据空气弹簧胶囊内帘线参数数据，设置Rebar单元帘线截面积、帘线间距、帘线角度等参数。

2.3. 空气弹簧各部件相互作用的设置

将空气弹簧中的气囊与活塞、气囊与盖板都使用绑定进行约束，又因为弹簧在工作时，气囊与盖板和活塞都会面与面的接触，因此要对他们之间的接触进行设定，定义它们之间接触属性中切向属性的摩擦公式为无摩擦，法向行为中压力过盈的种类为“硬”接触，同时气囊的内外面在工作过程中也会相接触，因此定义它们的接触类型为自接触。

对流体腔中理想气体分子量属性进行定义，并设置气囊的中心点为充气点，充气范围为气囊与活塞、盖板所围成的封闭内部空间。

2.4. 网格划分

网格单元体划分是采用离散化的思想将模型有限细化 [9] ，只有合理建立网格体系，才能从根本上提高结果的可靠性并降低计算时间。对于活塞与盖板，由于不是寿命分析需要关注的重点，在网格划分时采取较大的网格，设置为缩减积分单元C3D4。对于气囊，采取壳单元(Shell)的S4R单元，并对活塞与气囊、盖板与气囊的连接部分其进行网格局部细化。最后所创建的空气弹簧有限元模型如下图2所示。

3. 空气弹簧静力学分析

3.1. 垂向工况载荷确定

汽车行驶过程中，空气弹簧首先要充入一定的惰性气体，使空气弹簧腔体内部达到一定的压强，在不同的工况下，空气弹簧始终承受着垂向位移载荷的作用，在有限元软件Abaqus中对此过程的仿真操作步骤主要如下：

Figure 2. Gas spring finite element model

图2. 空气弹簧有限元模型

(1) 在分析步的初始步中将活塞与盖板的边界条件设置为全约束。

(2) 在分析步的初始步中将所模拟的惰性气体单元冲入到之前所指定的工作区域，直至气囊内部压强达到0.6 MP。

(3) 在分析步中的第二步中释放活塞轴向的自由度，同时给予活塞一个沿着轴线向上方向的位移载荷。

在Abaqus中完成以上步骤之后，由于涉及到气体属性，因此还需要对绝对零度以及通用气体常数进行设置，最后提交作业，进行求解，求解结果如下图3所示。

Figure 3. Cloud of air spring stress results

图3. 空气弹簧应力结果云图

通过空气弹簧的Mises云图可知，在此垂向载荷工况下，空气弹簧所受到的最大应力位于活塞与气囊接触的部分，所受到的应力值大小为7.5 MPa，因此空气弹簧最有可能在此处受到破坏，为保证其工作的可靠性需要对其进行进一步的疲劳寿命分析。

3.2. 空气弹簧垂向静刚度特性曲线

空气弹簧强度计算的目的是确保空气弹簧不会在工作中出现塑性变形和疲劳损坏，同时为了确保达到其具有所需的弹性，空气弹簧载荷及其变形曲线之间的关系称为空气弹簧特性曲线，特征曲线的斜率反映了空气弹簧的刚度。

通过对空气弹簧上活塞上的参考点的仿真的结果数据进行分析：

(1) 提取活塞上设置的参考点场输出垂向位移数据。

(2) 提取活塞上参考点场输出支反力数据。

(3) 以垂向位移数据为X轴，支反力数据为Y轴绘制空气弹簧的垂向刚度特性曲线，结果如下图4所示。

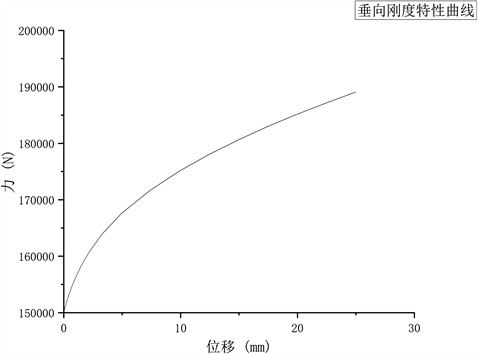
Figure 4. Vertical static stiffness characteristic curve of a gas spring

图4. 空气弹簧的垂向静刚度特性曲线

由空气弹簧的垂向刚度特性曲线图可知，弹簧的静刚度特性符合该车型对于该膜式空气弹簧的要求。由此可以证明所建立的空气弹簧的有限元模型是与实际相对符合的，验证了仿真模型的准确性。

4. 空气弹簧疲劳分析

4.1. 开裂能密度理论

开裂能密度理论(cracking energy density, CED) [10] 是基于断裂力学所提出的一种思想，该思想假设认定橡胶内部存在着初始的本征裂纹，且当橡胶产生疲劳破坏时，橡胶内部的裂纹慢慢成核一直到最后肉眼可见，紧接着裂纹不断的扩展，达到一定的程度后橡胶疲劳失效，而裂纹从成核直至达到破坏的程度时所循环的次数就是该橡胶材料的寿命。Mars和Fatemi最先将开裂能理论用于橡胶疲劳分析中，如图5所示。

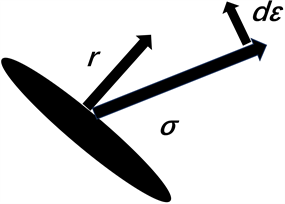
Figure 5. Schematic diagram of the cracking energy density parameter vector

图5. 开裂能量密度参量向量示意图

上图中 $\sigma$ 与 $\text{d}\epsilon$ 所代表的分别是所求解的该类型橡胶平面上的全应力矢量与应变增量矢量，而 代表其中所求解的橡胶所在平面内，任意一点所指定的裂纹平面的单位法向矢量。

$\text{d}{w}_c=\sigma \text{d}\epsilon$ (2)

公式(2)主要是用来表达开裂能的增量形式，其中w_c可以通过开裂能增量矢量对该裂纹所在平面的整个形变历史积分得到。

$T=-\frac{\text{d}U}{\text{d}A}=k{w}_{C}C$ (3)

公式(3)中参数U所代表的是产生裂纹的物体在受到拉伸时所具有的弹性能，而参数A为产生裂纹的物体的裂纹面积，参数k是一个几何参数，它主要和伸长比相关，参数w_C所代表的物理意义是开裂能，参数C所代表的是裂纹的长度，但该裂纹长度为其在外部载荷作用下，上次循环结束后的裂纹长度。

通过开裂能密度理论的相关定义，可以得知，开裂能数值的大小，同时与其单元中心所选取的平面以及应变历史都有一定的联系。因此首先基于开裂能理论计算每个单元中心所有可能开裂平面在应变峰值点的开裂能，再对所有在加载循环中可能产生断裂平面的撕裂能峰值T_max进行求解。

4.2. 结构疲劳寿命计算

为了计算橡胶的结构疲劳寿命首先需要对每个单元中心所有可能开裂平面的最大、最小撕裂能进行提取。

$\frac{\text{d}c}{\text{d}N}=\{\begin{array}{l}{r}_c{\left(\frac{T_{\text{eq}}}{T_{\text{c}}}\right)}^{F\left(R\right)}{T}_{\text{eq}}\le T_{\text{c}}\\ \infty T_{\text{eq}}>T_{\text{c}}\end{array}$ (4)

公式(4)是用来对裂纹增长速率进行计算的公式，其中R = T_min/T_max，参数r_c所代表的意义是裂纹失稳扩展前段临界速率，参数T_eq所代表的的意义是等效撕裂能，参数F(R)所代表的意义是R对裂纹增长率的影响，参数T_C所代表的意义是裂纹失稳扩展的临界撕裂能密度。

$T_{\text{eq}}=T_{\text{max}}^{\frac{F\left(R\right)}{F\left(0\right)}}{T}_{\text{C}}^{1-\frac{F\left(R\right)}{F\left(0\right)}}$ (5)

$F\left(R\right)=F_0+F_{1}R+F_2{R}^2+F_3{R}^3$ (6)

公式(4)中的参数T_eq与参数F(R)还可以通过公式(5)与(6)所示的函数进行表达，其中参数F₀、F₁R、F₂R²、F₃R³所代表的是与材料相关的常数，它们可以通过拟合不同载荷比值下的橡胶裂纹扩展试验得到。

$N={\displaystyle {\int }_{c_0}^{c_f}{\left(\frac{\text{d}c}{\text{d}N}\left(T_{\max ,\text{i},R_{\text{i}}}\right)\right)}^{-1}\text{d}c}$ (7)

公式(7)为开裂平面疲劳寿命N计算表达式，其中c_f为裂纹失稳扩展临界长度，c₀为初始裂纹长度。

由所计算的每个单元中心所有可能开裂平面的最大、最小撕裂能并通过上述公式(4)∼(6)可以分别对各平面单元的裂纹增长速率 $\text{d}c/\text{d}N\left(T_{\max ,\text{i},R_{\text{i}}}\right)$ 进行求解。最后，结合式(7)可求得单元中心所有可能开裂平面的疲劳寿命，同时定义该单元的开裂平面为疲劳寿命最短的平面，且橡胶结构中最先发生疲劳裂纹的平面即为所有单元中疲劳寿命最短的平面。

4.3. 空气弹簧的疲劳寿命仿真分析流程

使用Fe-safe软件对空气弹簧的寿命进行预测，具体操作流程如下：

(1) 将之前使用Abaqus在特定工况下空气弹簧非线性有限元仿真应力应变结果导出为obd*格式的文件，并导入到Fe-safe软件中，同时对空气弹簧的气囊部分以及活塞与盖板部分进行分组，以及单位的修改。

(2) 对空气弹簧各个部分的表面粗糙度进行定义，默认为1。

(3) 空气弹簧气囊部分所使用的橡胶为天然橡胶，Fe-safe本身自带的材料库中就有天然橡胶，因此直接可以选择其材料库中的天然橡胶。

(4) 算法选择Fe-safe中的自带的基于开裂能理论的Edurica算法，由于主要是计算弹簧的寿命，因此对于活塞与盖板部分定义为不计算。

(5) 使用空气弹簧有限元仿真的应力应变结果定义载荷。

4.4. 空气弹簧的疲劳寿命仿真结果

按照上诉疲劳仿真操作步骤，对空气弹簧进行疲劳寿命计算，最后经过仿真迭代计算，空气弹簧在该工况下的寿命为10^6.2次。同时Fesafe软件可以联合Abaqus软件对空气弹簧的仿真结果进行可视化查看，下图6为空气弹簧整体的寿命云图。

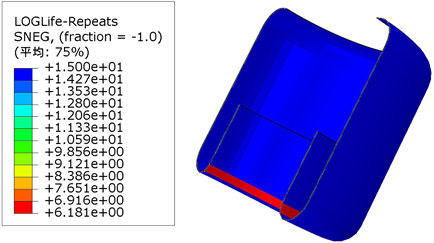
Figure 6. Visualize the life cloud of the rear gas spring

图6. 可视化后空气弹簧的寿命云图

由空气弹簧的寿命云图可知，其寿命最短的部分发生在活塞与气囊连接处，且由之前在Abaqus中的有限元仿真结果可知，气囊受到最大应力的部位也在此处，据此可以验证仿真的准确性。

5. 结论

本文进行了空气弹簧某工况下垂向位移下的静刚度特性分析及疲劳分析，并对空气弹簧主要是含橡胶部分的气囊进行了疲劳寿命评估，得到以下结论：

(1) 通过对建立的空气弹簧模型在特定工况下进行静力学分析，获得了空气弹簧的静刚度特性曲线且其静刚度特性与实际相符，验证了空气弹簧静力学仿真分析的准确性。

(2) 由静力学分析结果可知，在该垂向位移载荷工况下的最大应力位于活塞与气囊连接处，与实际空气弹簧长期使用后出现损伤的位置相似，因此在长期循环使用的情况下可能会发生疲劳断裂，需要对其寿命进行评估。

(3) 由疲劳分析结果可知，空气弹簧寿命最短的地方在活塞与气囊的连接处，其寿命为10^6.2次，理论上空气弹簧正常工作可循环次数应达到百万级别，因此仿真所计算的寿命与空气弹簧实际工作寿命处于一个量级，因此仿真结果对于空气弹簧的寿命预测具有一定参考意义。