Oto-Escaff-Cisternas模型的定性分析

The Qualitative Analysis of Oto-Escaff-Cisternas Model

摘要: 考虑Oto-Escaff-Cisternas植物–食草动物模型的动力学性质。首先，讨论了模型解的正性及有界性，分析对应平衡点处雅可比矩阵的特征值，给出了模型平衡点的拓扑类型；其次，应用分支分析的理论及解析方法，讨论了该模型的鞍结点分支和Hopf分支，得到了正平衡点的稳定性和Hopf分支的存在条件；再次，通过计算第一李雅普洛夫系数，证明了该系统会发生亚临界Hopf分支，并且在正平衡点附近产生了唯一一个不稳定的极限环。最后，对所获得的理论结果给出了数值模拟。

Abstract: In this paper, the dynamics properties of the Oto-Escaff-Cisternas plant-herbivore model are con-sidered. Firstly, the positiveness and boundedness of the model solution are discussed, the eigen-values of the Jacobian matrix at the corresponding equilibrium point are analyzed, and the topolog-ical type of the model equilibrium point is given. Secondly, via the analytical method of bifurcation analysis, the saddle node bifurcation and Hopf bifurcation of the model are discussed, and the sta-bility of the positive equilibrium point and the existence conditions of the Hopf bifurcation are ob-tained. Furthermore, by calculating the first Lyapunov coefficient, it is proved that the system will have a subcritical Hopf bifurcation and produce the only unstable limit ring near the positive equi-librium point. Finally, some numerical simulations were carried out to illustrate our theoretical re-sults.

1. 引言

植物和食草动物之间的相互作用是生态学中最基本的过程之一。在植物的生长发育过程中，随时会面临着各种生物和非生物的逆境胁迫，如人类的不合理活动(过度放牧、土地开垦等)以及干旱、高海拔和极端温度等非生物因素。这些逆境胁迫对植被的生长发育产生了严重影响，在不利环境下对植被状态的研究一直是生态系统动力学的一个重要课题，见文献 [1] - [7] 。因此，研究植被在不利环境下的动力学行为具有重要的理论意义和实际应用价值，有助于对生态系统的科学管理。1999年，美国生物数学家Klausmeier [8] 研究半干旱地区坡地上植被斑图的形成时，建立了如下水和植物之间的关系模型：

$\{\begin{array}{l}\frac{\partial N}{\partial T}=RJW{N}^2-\left(M+V\right)N+\delta \left(\frac{{\partial }^2}{\partial X^2}+\frac{{\partial }^2}{\partial Y^2}\right)N,\\ \frac{\partial W}{\partial T}=A-LW-RW{N}^2+U\frac{\partial W}{\partial X},\end{array}$ (1)

其中 $\left(X,Y\right)$ 表示空间坐标，T表示时间， $N\left(X,Y,T\right)$ 表示植物的密度，W表示土壤中可用到的水资源量，参数A表示降雨率，M表示没有食草动物时植物生物量的死亡率，V表示由食草动物引起的植物生物量的死亡率，R表示每单位植物生物量吸收的水量，RWN表示植物的吸水率，L是水的蒸发率，J是每吸收单位水资源量对植物生物量的转化效率，扩散系数 $\delta$ 代表植物的扩散能力，U是一个与地形坡度有关的系数。

2005年Sherratt [9] 对Klausmeier模型中的斑图形成进行了详细的理论分析，推导了预测斑图的波长和迁移速度的表达式，并系统地研究了它们与模型参数的关系；2011年，Sherratt [10] 对于特定的参数空间，推导出了Klausmeier模型出现斑图的参数区域及边界的表达式；2019年，Oto，Escaff和Cisterna [11] 在研究智利北部高海拔干旱条件下草生物量时，考虑了模型(1)在没有其他明确的空间依赖时，水资源量W的变化比植物生物量密度N快得多，对于给定的植物生物量密度值，水资源量处于一个平衡状态。假设地形是平坦的 $\left(U=0\right)$ ，得到 $W=\frac{A}{L+R{N}^2}$ ，并提出了如下植物–食草动物动力学模型：

$\{\begin{array}{l}\frac{\partial N}{\partial T}=RJW{N}^2-\left(M+V\right)N+\delta \left(\frac{{\partial }^2}{\partial X^2}+\frac{{\partial }^2}{\partial Y^2}\right)N,\\ \frac{\partial V}{\partial T}=CVN-KV,\end{array}$ (2)

其中 $V\left(X,Y,T\right)$ 表示食草动物的分布面积，食草动物的分布面积以CN的比率增加，以K的比率减少， $W=\frac{A}{L+R{N}^2}$ 。

考虑到系统(2)的生物意义，规定模型中所有参数均为正，引入无量纲变化：

$N=\sqrt{\frac{L}{R}}n,x=\sqrt{\frac{C}{\delta }\sqrt{\frac{L}{R}}}X,y=\sqrt{\frac{C}{\delta }\sqrt{\frac{L}{R}}}Y,M=C\sqrt{\frac{L}{R}}m,t=C\sqrt{\frac{L}{R}}T,A=\frac{CL}{JR}a,V=C\sqrt{\frac{L}{R}}v,K=C\sqrt{\frac{L}{R}}k.$

在不考虑空间变量和耗散的情况下，他们将系统(2)转化为如下形式：

$\{\begin{array}{l}\frac{\text{d}n}{\text{d}t}=\frac{a{n}^2}{1+n^2}-\left(m+v\right)n,\\ \frac{\text{d}v}{\text{d}t}=vn-kv,\end{array}$ (3)

并分析了系统(3)四个平衡点的稳定性。然而，关于模型(3)还有如下一些问题：

(a) 平衡点的拓扑类型是怎么样的？

(b) 当参数变化时，系统会产生什么样的分支？

基于以上分析考虑，本文讨论了系统(3)的雅可比矩阵在平衡点处的特征值，并给出了这些点的拓扑类型；通过计算第一李雅普洛夫系数，证明了系统(3)会产生亚临界Hopf分支及在正平衡点附近产生了唯一一个极限环；通过数值模拟展示了这个极限环，从而验证了理论结果。

2. 系统解的正性和有界性

在分析系统(3)平衡点的拓扑类型之前，首先证明在 ${ℝ}_{+}^2=\left\{\left(n,v\right)\in {ℝ}^2:n\ge 0,v\ge 0\right\}$ 上，闭的第一象限是该系统的一个正不变集。

定理1 如果系统(3)满足初始条件 $n\left(0\right)=n_0\ge 0,v\left(0\right)=v_0\ge 0$ ，那么对于所有的 $t>0$ ，系统(3)的每个解都是非负的。

证明 从系统(3)的第一个方程式中，可得

$\frac{\text{d}n\left(t\right)}{\text{d}t}=\frac{a{\left[n\left(t\right)\right]}^2}{1+{\left[n\left(t\right)\right]}^2}-\left[m+v\left(t\right)\right]n\left(t\right)\ge -\left[m+v\left(t\right)\right]n\left(t\right)$ ,

则

$\frac{\text{d}n\left(t\right)}{\text{d}t}+\left[m+v\left(t\right)\right]n\left(t\right)\ge 0$ . (4)

令 $F\left(t\right)=m+v\left(t\right)$ 。给(4)式两边分别乘以 $\exp \left({\displaystyle {\int }_0^{t}F\left(s\right)\text{d}s}\right)$ ，得到

$\exp \left({\displaystyle {\int }_0^{t}F\left(s\right)\text{d}s}\right)\cdot \frac{\text{d}n\left(t\right)}{\text{d}t}+F\left(t\right)\cdot \exp \left({\displaystyle {\int }_0^{t}F\left(s\right)\text{d}s}\right)\cdot n\left(t\right)\ge 0$ ,

则有

$\frac{\text{d}}{\text{d}t}\left(\exp \left({\displaystyle {\int }_0^{t}F\left(s\right)\text{d}s}\right)\cdot n\left(t\right)\right)\ge 0$ . (5)

将(5)式从0到t积分

${\displaystyle {\int }_0^t\frac{\text{d}}{\text{d}s}}\left(\exp \left({\displaystyle {\int }_0^{s}F\left(u\right)\text{d}u}\right)\cdot n\left(s\right)\right)\text{d}s\ge 0$ ,

最后得到

$n(t)\ge n\left(0\right)\cdot \exp \left(-{\displaystyle {\int }_0^t\left(m+v\left(s\right)\right)}\right)\text{d}s\ge 0$ .

同理可证 $v\left(t\right)\ge 0$ 。证毕。

定理2 系统(3)在满足初始条件 $\left(n_0,v_0\right)\in {ℝ}_{+}^2$ 下的正解是有界的。

证明 构造函数 $N\left(t\right)=n\left(t\right)+v\left(t\right)$ ，沿系统(3)对 $N\left(t\right)$ 求导得

$\stackrel{\dot{}}{N}\left(t\right)=\stackrel{\dot{}}{n}\left(t\right)+\stackrel{\dot{}}{v}\left(t\right)=\frac{a{n}^2}{1+n^2}-mn-kv\le a-mn-kv\le a-\delta N\left(t\right)$ ,

其中 $\delta =\min \left\{m,k\right\}$ ，故有 $\stackrel{\dot{}}{N}\left(t\right)+\delta N\left(t\right)\le a$ 。

当 $t>0$ 时，由微分不等式理论，可得

$N(t)\le \frac{a}{\delta }\left(1-{\text{e}}^{-\delta t}\right)+N_0\cdot {\text{e}}^{-\delta t}$ ,

当 $t\to +\infty$ 时，有

$\underset{t\to +\infty }{\lim }N\left(t\right)\le \frac{a}{\delta }$ ,

又因为 $n\left(t\right)\ge 0,v\left(t\right)\ge 0$ ，所以 $n\left(t\right),v\left(t\right)$ 最终是有界的。证毕。

3. 平衡点的定性性质

下面考虑系统(3)平衡点的定性性质。首先，系统(3)始终存在平衡点 $E_1\left(0,0\right)$ 。

当 $a>2m$ 时，平衡点

$E_2\left(\frac{a+\sqrt{a^2-4m^2}}{2m},0\right)$ , $E_3\left(\frac{a-\sqrt{a^2-4m^2}}{2m},0\right)$ ,

存在，且当 $ak>m\left(1+k^2\right)$ 时，系统存在唯一的正平衡点

$E_4\left(n^{*},v^{*}\right)=\left(k,\frac{ak}{1+k^2}-m\right)$ .

系统(3)在平衡点 $E\left(n,v\right)$ 线性化后对应的雅可比矩阵为

$J\left(E\right)=\left(\begin{array}{cc}\frac{2an}{{\left(1+n^2\right)}^2}-\left(m+v\right)& -n\\ v& n-k\end{array}\right)$ . (6)

下面通过矩阵(6)讨论该系统四个平衡点的拓扑类型。

定理3 平衡点 $E_1\left(0,0\right)$ 是一个稳定结点。

证明 由(6)可得系统(3)在 $E_1\left(0,0\right)$ 的雅可比矩阵为

$J\left(E_1\right)=\left(\begin{array}{cc}-m& 0\\ 0& -k\end{array}\right)$ . (7)

显然，矩阵(7)存在两个负特征值。因此平衡点 $E_1\left(0,0\right)$ 是稳定的结点。

定理4 如果 $a>2m$ ，那么平衡点 $E_2$ 的拓扑类型如下：

1) 若 $k>\frac{a+\sqrt{a^2-4m^2}}{2m}$ ，则平衡点 $E_2$ 是一个稳定结点；

2) 若 $k<\frac{a+\sqrt{a^2-4m^2}}{2m}$ ，则平衡点 $E_2$ 是一个鞍点；

3) 若 $k=\frac{a+\sqrt{a^2-4m^2}}{2m}$ ，则平衡点 $E_2$ 是一个鞍结点。

证明 由(6)可得系统(3)在平衡点 $E_2$ 的雅可比矩阵为：

$J\left(E_2\right)=\left(\begin{array}{cc}-\frac{2m\left(\left(a^2-2m^2\right)\sqrt{a^2-4m^2}+a^3-4a{m}^2\right)}{a{\left(a+\sqrt{a^2-4m^2}\right)}^2}& -\left(\frac{a+\sqrt{a^2-4m^2}}{2m}\right)\\ 0& \frac{a+\sqrt{a^2-4m^2}}{2m}-k\end{array}\right)$ . (8)

下面分三种情形来讨论平衡点 $E_2$ 的拓扑类型：

1) 当 $k>\frac{a+\sqrt{a^2-4m^2}}{2m}$ 时，矩阵(8)的特征值为

${\lambda }_1=-\frac{2m\left(\left(a^2-2m^2\right)\sqrt{a^2-4m^2}+a^3-4a{m}^2\right)}{a{\left(a+\sqrt{a^2-4m^2}\right)}^2}<0,{\lambda }_2=\frac{a+\sqrt{a^2-4m^2}}{2m}-k<0$ .

因此平衡点 $E_2$ 是一个稳定结点；

2) 当 $k<\frac{a+\sqrt{a^2-4m^2}}{2m}$ 时，矩阵(8)存在两个异号实根。因此平衡点 $E_2$ 是一个鞍点；

3) 当 $k=\frac{a+\sqrt{a^2-4m^2}}{2m}$ 时， ${\lambda }_2=0$ 。此时平衡点 $E_2$ 是一个退化平衡点。

对系统(3)进行平移变换 $x=n-\frac{a+\sqrt{a^2-4m^2}}{2m},y=v$ ，再对系统(3)的右端函数在 $\left(0,0\right)$ 处进行泰勒展开，可得

$\{\begin{array}{l}\stackrel{\dot{}}{x}=-\frac{m\left(2a^2-8m^2+2a\sqrt{a^2-4m^2}\right)}{2a^2+2a\sqrt{a^2-4m^2}}x-\frac{\left(a+\sqrt{a^2-4m^2}\right)}{2m}y+\frac{2m^2\left(a^2-8m^2-a\sqrt{a^2-4m^2}\right)}{a\left(2a^2+2a\sqrt{a^2-4m^2}\right)}{x}^2-xy+o\left({\left|x,y\right|}^2\right),\\ \stackrel{\dot{}}{y}=xy.\end{array}$ (9)

其次， $J\left(E_2\right)$ 的特征值 ${\lambda }_1,{\lambda }_2$ 相对应的特征向量分别为 $V={\left(1,0\right)}^{\text{T}},W={\left(N,-M\right)}^{\text{T}}$ 。

对(9)式做线性变换 $x_1=x+\frac{N}{M}y,y_1=-\frac{1}{M}y$ ，可得

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=P{x}_1+Q{x}_1^2+\left(M+2NQ-N\right)x_1{y}_1+\left(MN-Q{N}^2-N^2\right)y_1^2+o\left({\left|x_1,y_1\right|}^2\right),\\ {\stackrel{\dot{}}{y}}_1=-M{x}_1{y}_1-MN{y}_1^2.\end{array}$

其中

$M=-\frac{2m\left(\left(a^2-2m^2\right)\sqrt{a^2-4m^2}+a^3-4a{m}^2\right)}{a{\left(a+\sqrt{a^2-4m^2}\right)}^2},N=\frac{-a-\sqrt{a^2-4m^2}}{2m},$

$P=-\frac{m\left(2a^2-8m^2+2a\sqrt{a^2-4m^2}\right)}{2a^2+2a\sqrt{a^2-4m^2}},Q=\frac{2m^2\left(a^2-8m^2-a\sqrt{a^2-4m^2}\right)}{a\left(2a^2+2a\sqrt{a^2-4m^2}\right)}$ .

然后，令 $\tau =pt$ ，再用 $t$ 表示 $\tau$ ，则有

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1=x_1+\frac{Q}{P}{x}_1^2+\frac{\left(M+2NQ-N\right)}{P}{x}_1{y}_1+\frac{\left(MN-Q{N}^2-N^2\right)}{P}{y}_1^2+o\left({\left|x_1,y_1\right|}^2\right),\\ {\stackrel{\dot{}}{y}}_1=-\frac{M}{P}{x}_1{y}_1-\frac{MN}{P}{y}_1^2.\end{array}$

而 $y_1^2$ 的系数

$-\frac{MN}{P}=\frac{\left(a^2-2m^2\right)\sqrt{a^2-4m^2}+a^3-4a{m}^2}{\left(a\sqrt{a^2-4m^2}+a^2-4m^2\right)m}>0$ ,

故当 $k=\frac{a+\sqrt{a^2-4m^2}}{2m}$ 时，平衡点 $E_2$ 是一个鞍结点。

定理5 如果 $a>2m$ ，那么平衡点 $E_3$ 的拓扑类型如下：

1) 若 $k>\frac{a-\sqrt{a^2-4m^2}}{2m}$ ，则平衡点 $E_3$ 是一个鞍点；

2) 若 $k<\frac{a-\sqrt{a^2-4m^2}}{2m}$ ，则平衡点 $E_3$ 是一个不稳定结点；

3) 若 $k=\frac{a-\sqrt{a^2-4m^2}}{2m}$ ，则平衡点 $E_3$ 是一个鞍结点。

证明 由(6)可得系统(3)在平衡点 $E_3$ 的雅可比矩阵为：

$J\left(E_3\right)=\left(\begin{array}{cc}-\frac{2m\left(\left(-a^2+2m^2\right)\sqrt{a^2-4m^2}+a^3-4a{m}^2\right)}{a{\left(a-\sqrt{a^2-4m^2}\right)}^2}& -\left(\frac{a-\sqrt{a^2-4m^2}}{2m}\right)\\ 0& \frac{a-\sqrt{a^2-4m^2}}{2m}-k\end{array}\right)$ .

类似于定理4的证明可得：当 $k>\frac{a-\sqrt{a^2-4m^2}}{2m}$ 时，平衡点 $E_3$ 是一个鞍点；当 $k<\frac{a-\sqrt{a^2-4m^2}}{2m}$ 时，平衡点 $E_3$ 是一个不稳定结点；当 $k=\frac{a-\sqrt{a^2-4m^2}}{2m}$ 时，平衡点 $E_3$ 是一个鞍结点。

下面讨论正平衡点 $E_4$ 的拓扑类型.

定理6当 $ak>m\left(1+k^2\right)$ 时，正平衡点 $E_4$ 的拓扑类型如下表1所示：

Table 1. Topology type of the positive equilibrium point E 4

表1. 正平衡点 $E_4$ 的拓扑类型

其中 $\Lambda ={\left(\frac{ak\left(1-k^2\right)}{{\left(1+k^2\right)}^2}\right)}^2+\frac{4k\left(m+m{k}^2-ak\right)}{1+k^2}$ 。

证明 由(6)可得系统(3)在 $E_4$ 的雅可比矩阵为

$J\left(E_4\right)=\left(\begin{array}{cc}\frac{ak\left(1-k^2\right)}{{\left(1+k^2\right)}^2}& -k\\ \frac{ak}{1+k^2}-m& 0\end{array}\right)$ (10)

则矩阵(10)的特征方程为：

${\lambda }^2-T\lambda +D=0$ . (11)

其中

$T=\frac{ak\left(1-k^2\right)}{{\left(1+k^2\right)}^2},D=\frac{a{k}^2}{1+k^2}-mk.$

通过计算可得(11)的特征值为

${\lambda }_1=\frac{1}{2}\left(T-\sqrt{T^2-4D}\right)$ , ${\lambda }_2=\frac{1}{2}\left(T+\sqrt{T^2-4D}\right)$ .

下面分三种情形来讨论正平衡点 $E_4$ 的拓扑类型：

1) 当 $\Lambda >0$ 时，若 $k<1$ ，则矩阵(10)存在两个不相等的正实根，因此平衡点 $E_4$ 是一个不稳定结点；若 $k=1$ ，则 $\mathrm{Re}\left({\lambda }_i\right)=0,{\lambda }_{1,2}=\pm i\frac{1}{2}\sqrt{2a-4m}$ ，因此平衡点 $E_4$ 是一个中心；若 $k>1$ ，则矩阵(10)存在两个负实根，因此平衡点 $E_4$ 是一个稳定结点。

2) 当 $\Lambda =0$ 时， ${\lambda }_1={\lambda }_2=\frac{ak\left(1-k^2\right)}{2{\left(1+k^2\right)}^2}$ 。若 $k<1$ ，则 ${\lambda }_1={\lambda }_2>0$ ，因此平衡点 $E_4$ 是一个不稳定退化结点。若 $k=1$ ，则 ${\lambda }_1={\lambda }_2=0$ ，因此平衡点 $E_4$ 是一个退化平衡点。若 $k>1$ ，则 ${\lambda }_1={\lambda }_2<0$ ，因此平衡点 $E_4$ 是一个稳定退化结点。

3) 当 $\Lambda <0$ 时，

${\lambda }_1=\frac{1}{2}\left(T-i\sqrt{4D-T^2}\right),{\lambda }_2=\frac{1}{2}\left(T+i\sqrt{4D-T^2}\right)$ .

此时， $\mathrm{Re}\left({\lambda }_1\right)=\mathrm{Re}\left({\lambda }_2\right)=\frac{ak\left(1-k^2\right)}{2{\left(1+k^2\right)}^2}$ ，若 $k<1$ ，则 $\mathrm{Re}\left({\lambda }_i\right)>0$ ，因此平衡点 $E_4$ 是一个不稳定焦点。若 $k=1$ ，则 $\mathrm{Re}\left({\lambda }_i\right)=0$ ，因此平衡点 $E_4$ 是一个中心。若 $k>1$ ，则 $\mathrm{Re}({\lambda }_i)<0$ ，因此平衡点 $E_4$ 是一个稳定焦点。

4. 正平衡点的稳定性和Hopf分支

由定理6可知，当 $ak>m\left(1+k^2\right)$ 时， $D>0$ ，所以当 $T<0$ 时，正平衡点 $E_4$ 是稳定的；当 $T>0$ 时，正平衡点 $E_4$ 是不稳定的。若 $T=0$ ，当参数 $k$ 满足 $k=1$ 时，特征方程(13)有一对纯虚根 ${\lambda }_{1,2}=\pm i\frac{1}{2}\sqrt{2a-4m}$ 。

下面通过取 $k$ 为分支参数来考虑系统(3)正平衡点 $E_4$ 的稳定性和Hopf分支。

记特征值的表达式为 $\lambda \left(k\right)=\mu \left(k\right)\pm iw\left(k\right)$ ，其中 $\mu \left(k\right)=\frac{1}{2}T,w\left(k\right)=\frac{1}{2}\sqrt{4D-T^2}$ 。因此，当 $k=1$ 时，有 $\mu \left(1\right)=0,w^2\left(1\right)=\frac{a}{2}-m>0$ ，横截性条件容易验证

${\mu }^{\prime }\left(k\right)=\frac{a\left(k^4-6k^2+1\right)}{2{\left(k^2+1\right)}^3}$ ,

故 ${\mu }^{\prime }\left(1\right)=-\frac{a}{4}<0$ 。

由Poincare-Andronov-Hopf分支定理 [12] 可知，当 $k=1$ 时，系统(3)在平衡点 $E_4$ 处存在Hopf分支。

接下来讨论当 $k=1$ 时，系统(3)在平衡点 $E_4$ 附近会有Hopf分支以及极限环的产生。

首先，令 $n=x+n^{*},v=y+v^{*}$ ，则系统(3)化为：

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=\frac{a{\left(x+1\right)}^2}{1+{\left(x+1\right)}^2}-\left(y+\frac{a}{2}\right)\left(x+1\right),\\ \frac{\text{d}y}{\text{d}t}=\left(y+\frac{a}{2}-m\right)\left(x+1\right)-\left(y+\frac{a}{2}-m\right),\end{array}$ (12)

然后，对系统(12)的右端函数在 $\left(0,0\right)$ 处进行泰勒展开，则系统(12)就可以写为

$\{\begin{array}{l}\frac{\text{d}x}{\text{d}t}=a_{1}x+a_{2}y+f_1\left(x,y\right),\\ \frac{\text{d}y}{\text{d}t}=b_{1}x+b_{2}y+f_2\left(x,y\right),\end{array}$ (13)

其中 $a_1=0,a_2=-1,b_1=\frac{a}{2}-m,b_2=0,f_1\left(x,y\right)=-xy-\frac{1}{4}a{x}^2+\frac{1}{8}a{x}^4-\frac{1}{8}a{x}^5,f_2\left(x,y\right)=xy.$

系统(13)在 $E_4\left(n^{*},v^{*}\right)$ 处线性化的雅可比矩阵为 $L=\left(\begin{array}{cc}0& -1\\ \frac{1}{2}a-m& 0\end{array}\right)$ ，此时L在复数域C存在两个非零特征根 ${\lambda }_{1，2}=\pm \frac{1}{2}\sqrt{-2a+4m}$ ，根据线性代数中的Jordan标准性理论可知，存在非奇异线性变换H。

下一步进行线性变换，取变换矩阵

$H=\left(\begin{array}{cc}1& 0\\ 0& \frac{1}{2}\sqrt{2a-4m}\end{array}\right),H^{-1}=\left(\begin{array}{cc}1& 0\\ 0& \frac{2}{\sqrt{2a-4m}}\end{array}\right)$ ,

则

$H^{-1}LH=Q\left(h\right)=\left(\begin{array}{cc}0& -\frac{1}{2}\sqrt{2a-4m}\\ \frac{1}{2}\sqrt{2a-4m}& 0\end{array}\right)$ .

作变换 ${\left(x,y\right)}^{\text{T}}=H{\left(u,w\right)}^{\text{T}}$ ，则系统(13)转化为

$\left(\begin{array}{c}\frac{\text{d}u}{\text{d}t}\\ \frac{\text{d}w}{\text{d}t}\end{array}\right)=Q\left(h\right)\left(\begin{array}{c}u\\ w\end{array}\right)+\left(\begin{array}{c}{f}_1\left(u,w\right)\\ f_2\left(u,w\right)\end{array}\right)$ ,

即

$\{\begin{array}{l}\frac{\text{d}u}{\text{d}t}=-\frac{1}{2}\sqrt{2a-4m}w+f_1\left(u,w\right),\\ \frac{\text{d}w}{\text{d}t}=\frac{1}{2}\sqrt{2a-4m}u+f_2\left(u,w\right).\end{array}$ (14)

其中 $a_1=0,a_2=-\frac{1}{2}\sqrt{2a-4m},b_1=\frac{1}{2}\sqrt{2a-4m},b_2=0,f_1\left(u,w\right)=-\frac{1}{4}a{u}^2-\frac{1}{2}\sqrt{2a-4m}uw,f_2\left(u,w\right)=uw.$

将系统(14)写为极坐标形式：

$\{\begin{array}{l}\stackrel{\dot{}}{r}=\mu \left(k\right)r+a\left(k\right)r^3+\cdots ,\\ \stackrel{\dot{}}{\theta }=w\left(k\right)+b\left(k\right)r^2+\cdots .\end{array}$ (15)

在 $k=1$ 处展开(15)式的右端函数，可得

$\{\begin{array}{l}\stackrel{\dot{}}{r}={\mu }^{\prime }\left(1\right)\left(k-1\right)r+a\left(1\right)r^3+\cdots ,\\ \stackrel{\dot{}}{\theta }=w\left(1\right)+{\mu }^{\prime }\left(1\right)(k-1)+b\left(1\right)r^2+\cdots .\end{array}$

进而求得

$\begin{array}{c}a\left(1\right)=\frac{1}{16}\left[f_{uuu}^1+f_{uww}^1+f_{uuw}^2+f_{www}^2\right]+\frac{1}{16w}\left[f_{uw}^1\left(f_{uu}^1+f_{ww}^1\right)-f_{uw}^2\left(f_{uu}^2+f_{ww}^2\right)-f_{uu}^1{f}_{uu}^2+f_{ww}^1{f}_{ww}^2\right]{|}_{(0,0,1)}\\ =\frac{1}{16\cdot \frac{1}{2}\sqrt{2a-4m}}\cdot \frac{a\sqrt{2a-4m}}{4}=\frac{a}{32}>0.\end{array}$

因此，根据Poincare-Andronov-Hopf分支定理 [12] ，可得如下结论：

定理7(1) 如果 $k>1$ ，那么系统(3)的平衡点 $E_4$ 是局部渐近稳定的，同时在平衡点 $E_4$ 附近分支出一个不稳定的极限环，系统(3)将会产生亚临界Hopf分支。

(2) 如果 $0<k<1$ ，那么系统(3)的平衡点 $E_4$ 是不稳定的。

(3) 如果 $k=1$ ，那么系统(3)的平衡点 $E_4$ 有特征值 ${\lambda }_{1,2}=\pm i\frac{1}{2}\sqrt{2a-4m}$ ，并且系统(3)将在正平衡点 $E_4$ 附近产生Hopf分支。

5. 鞍结点分支

引理1 [13] 考虑系统 $\frac{\text{d}x}{\text{d}t}=f\left(x,\mu \right)$ ，其中 $x\in {ℝ}^n,\mu \in R$ ，并且f为光滑函数。

假设 $f\left(x_0,{\mu }_0\right)=0$ ，且它对应的雅可比矩阵 $J=Df\left(x_0,{\mu }_0\right)$ 只有一个零特征根。如果矩阵 $J$ 和 $J^{\text{T}}$ 的零特征根所对应的特征向量 $V$ ， $W$ 使得下面条件成立：

(i) $W^{\text{T}}{f}_{\mu }\left(x_0,{\mu }_0\right)\ne 0$ ；

(ii) $W^{\text{T}}\left[D^2{f}_{\mu }\left(x_0,{\mu }_0\right)\left(v,v\right)\right]\ne 0$ 。

那么，当参数 $\mu$ 经过分支参数 ${\mu }_0$ 时，系统在平衡点 $x_0$ 处将会经历一个鞍结点分支。

定理8 平衡点 $E_2$ 在 $a=a_c$ 处产生鞍结点分支，其中 $a_c=2m$ 。

证明 选择 $a$ 作为分支参数，利用Sotomayor定理证明系统(3)产生了鞍结点分支，当 $a=a_c$ 时，系统(3)在平衡点 $E_2$ 处存在一个零特征根，即雅可比矩阵变为

$J_2=\left(\begin{array}{cc}0& -1\\ 0& 1-k\end{array}\right)$ .

假设 $V$ 和 $W$ 分别是 $J_2$ 和 $J_2^{\text{T}}$ 相对于零特征根的特征向量

$V=\left(\begin{array}{c}{v}_1\\ v_2\end{array}\right)=\left(\begin{array}{c}1\\ 0\end{array}\right),W=\left(\begin{array}{c}{w}_1\\ w_2\end{array}\right)=\left(\begin{array}{c}1\\ -\frac{1}{k-1}\end{array}\right)$ ,

令 $F\left(n,v\right)=\left(\begin{array}{c}{F}_1\\ F_2\end{array}\right)=\left(\begin{array}{c}\frac{a{n}^2}{1+n^2}-\left(m+v\right)n\\ vn-kv\end{array}\right)$ ，

通过计算可得

$F_a\left(E_2;a_c\right)={\left(\begin{array}{c}\frac{\partial F_1}{\partial a}\\ \frac{\partial F_2}{\partial a}\end{array}\right)}_{(E_2;a_c)}=\left(\begin{array}{c}\frac{1}{2}\\ 0\end{array}\right)$ ,

$D^{2}F\left(E_2;a_c\right)\left(v,v\right)={\left(\begin{array}{c}\frac{{\partial }^2{F}_1}{\partial n^2}{v}_1{v}_1+2\frac{{\partial }^2{F}_1}{\partial n\partial v}{v}_1{v}_2+\frac{{\partial }^2{F}_1}{\partial v^2}{v}_2{v}_2\\ \frac{{\partial }^2{F}_2}{\partial n^2}{v}_1{v}_1+2\frac{{\partial }^2{F}_2}{\partial n\partial v}{v}_1{v}_2+\frac{{\partial }^2{F}_2}{\partial v^2}{v}_2{v}_2\end{array}\right)}_{(E_2;a_c)}=\left(\begin{array}{c}-m\\ 0\end{array}\right)$ ,

从而有 $W^T\left[F_a\left(E_2;a_c\right)\right]=\frac{1}{2}>0$ ，这意味着系统(3)在 $E_2$ 处不会发生跨临界分支。进一步，有

$W^{\text{T}}\left[D^{2}F\left(E_2;a_c\right)\left(v,v\right)\right]=-m<0$ .

所以，根据Sotomayor定理可知，当参数 $a=a_c$ 时，系统(3)在平衡点 $E_2$ 附近产生了鞍结点分支；当 $a>a_c$ 时，系统有两个平衡点 $E_2,E_3$ ，并且当 $a=a_c$ 时，这两个平衡点碰撞重合；当 $a<a_c$ 时，系统(3)的两个平衡点消失。

6. 数值模拟

这一节利用Maple软件包对理论分析进行相应的数值模拟。

在系统(3)中选取参数 $a=10,m=3,k=0.913$ ，满足系统有唯一的正平衡点 $E_4$ ，当 $k=0.913<1$ 时，由定理7知正平衡点 $E_4\left(0.913,1.979\right)$ 是不稳定的，如图1所示。当 $k$ 增大到临界值1时，正平衡点 $E_4\left(1,2\right)$ 失稳并经历Hopf分支，进一步计算得 $a\left(1\right)=0.3125>0$ ，则由定理7知Hopf分支是亚临界的。当 $k=1.01>1$ 时，系统(3)的正平衡点 $E_4\left(1.010000,1.999752\right)$ 是局部渐近稳定的，且系统(3)存在一个不稳定的极限环，如图2所示。

Figure 1. Positive equilibrium point of system (3) is unstable when parameter $k=0.913$

图1. 当参数 $k=0.913$ 时系统(3)的正平衡点不稳定

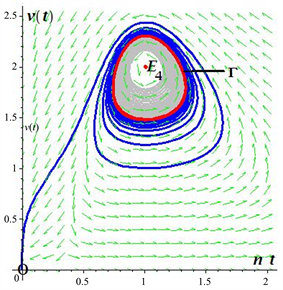
Figure 2. Positive equilibrium point of system (3) is locally asymptotically stable when parameter $k=1.01$

图2. 当参数 $k=1.01$ 时系统(3)的正平衡点局部渐近稳定

7. 结论

本文研究了Oto-Escaff-Cisternas植物–食草动物模型的动力学性质。首先，通过微分不等式理论给出了系统解的正性和有界性。其次，讨论了该模型四个平衡点的拓扑类型，给出了正平衡点的稳定性。进一步，当参数满足一定条件时，用分支理论证明了系统在平衡点 $E_2$ 附近会产生鞍结点分支，在平衡点 $E_3$ 处产生Hopf分支。最后，通过计算第一李雅普洛夫系数，证明了系统会发生亚临界的Hopf分支及在正平衡点附近产生了唯一一个不稳定的极限环。

基金项目

国家自然科学基金(11801243)；甘肃省高等学校青年博士项目(2022QB-056)。

参考文献

NOTES

^*第一作者。

^#通讯作者。