Tempered分数阶微分方程Nagumo型唯一解

Nagumo-Type Uniqueness Result for Tempered Fractional Differential Equations

摘要: 本文重点讨论Tempered分数阶微分方程柯西问题Nagumo迭代近似值的唯一性和收敛性。首先把柯西问题转化成等价Volterra积分方程，证出解的唯一性。然后，运用迭代方法，我们将Nagumo型唯一性和迭代近似值序列扩展到Tempered分数阶微分方程。

Abstract: This work is concerned with Nagumo-type uniqueness and convergence of successive approxima-tions to Cauchy problem for Tempered fractional differential equations. Firstly, to prove the uniqueness of the solution, the Cauchy problem is transformed into an equivalent Volterra integral equation. Then, using the iterative method, we extend Nagumo-type uniqueness and convergence of successive approximations to Tempered fractional differential equations.

1. 引言

分数阶导数是一个重要的数学工具，它具有一些非常有用的性质。分数阶导数具有非局域性，也就是说，它能够反映物理量在整个空间范围内的变化情况。相比于整数阶导数，分数阶导数可以更好地描述非局部的物理现象，如扩散、传输和耗散等。分数阶导数发展出几种不同类型的分数阶导数：如Riemann-Liouville分数阶、Caputo型分数阶导数( [1] )、Riesz型分数阶导数( [2] )以及Hilfer分数阶导数( [3] )。现在广泛使用的一种分数阶导数的定义是Riemann-Liouville分数阶积分与导数。函数在区间 $\left[0,T\right]$ 的 $0<\alpha <1$ 阶Riemann-Liouville分数阶积分与导数的定义为( [4] [5] )：

$I_{0+}^{\alpha }x\left(t\right)=\frac{1}{\Gamma \left(\alpha \right)}{\displaystyle {\int }_0^t{\left(t-s\right)}^{\alpha -1}}x\left(s\right)\text{d}s$

和

$D_x^{\alpha }\left(t\right)=D{I}_{0+}^{1-\alpha }x(\; t\; )$

其中 $D=\frac{\mathrm{d}}{\text{d}t}$ 。此后，分数阶微积分开始在各个领域得到应用。例如，在物理学中，分数阶微积分被用于

描述扩散过程、黏弹性材料、地震等。在工程学中，它被用于控制系统的稳定性分析、信号处理等。这类方程能更准确地描述某些现象，因为它们考虑了记忆效应和遗传效应。

分数阶导数在物理背景与实验数据进一步吻合的过程中修正和发展，其中就拓展出Tempered分数阶导数与积分。据我们所知，Buschman在文献 [6] 中首次提出具有弱奇异核和指数核的分数阶积分的定义。目前为止，Tempered型分数阶导数在基本性质、初值问题、边值问题和中值问题解的存在性、解的数值计算等等方面取得部分成果，其中Tempered分数阶微分方程的柯西问题有助于我们更深入地理解分数阶微分方程的性质和行为，这包括了解的唯一性、稳定性、收敛性等。Tempered分数阶微分方程可以描述许多具有记忆和遗传特性的复杂现象，它在处理某些具有特定衰减特性的问题时非常有用。例如材料科学、生物医学、工程控制等领域。研究Nagumo迭代近似值的唯一性和收敛性可以为实际问题的求解提供有效方法和理论支持，从而提高求解分数阶微分方程的效率和精度。因此，本文将Nagumo型迭代近似值的唯一性和收敛性从分数阶微分方程推广到Tempered分数阶微分方程。

例如，在 [7] 中，J. Chu和Z. W证明了半无限区间上非线性二阶微分方程

$\{\begin{array}{l}{x}^{″}=f\left(t,x\right),t\ge t_0\ge 0\\ x\left(t_0\right)=x_0\\ \underset{t\to \infty }{\lim }x\left(t\right)={\psi }_0,\underset{t\to \infty }{\lim }{x}^{\prime }\left(t\right)\exp \left(t\right)=0,{\psi }_0\in ℝ\end{array}$ (1.1)

Nagumo型唯一性解。

后来，V. Lakshmikantham和S. Leela把Nagumo型迭代近似值的唯一性和收敛性推广到分数阶微分方程：

$\{\begin{array}{l}{D}^{\alpha }x=f\left(t,x\right),0<\alpha <1，\\ x\left(t_0\right)=x_0={x\left(t\right){\left(t-t_0\right)}^{1-\alpha }|}_{t=t_0}.\end{array}$ (1.2)

受此启发，本文证明了Tempered分数阶微分方程柯西问题Nagumo迭代近似解的唯一性和收敛性。首先，通过将柯西问题转化为等价的积分方程，证明了该方程解的唯一性。然后，利用迭代方法，证明了迭代Nagumo近似值序列的唯一性和收敛性，并收敛于该积分方程的唯一解。这些结果表明，对于Tempered分数阶微分方程柯西问题，可以通过迭代方法得到唯一且收敛的近似解。

本文结构如下：第二节介绍了Tempered分数阶导数的定义(定义2.1)以及Tempered分数阶微分方程的等价Volterra积分方程(引理2.2)，第三节介绍了本文的主要结果Tempered分数阶微分方程Nagumo型迭代近似值的唯一性和收敛性。

2. 预备知识

本节给出Tempered分数阶导数定义和引理。以下均假设 $0<q<1$ ，参数 $\lambda \ge 0$ 为正数，设可积空间 $L\left(\left[a,b\right]\right)$ ，其中包括有限区间 $\left[a,b\right]$ 上的勒贝格可测函数，

$L\left(\left[a,b\right]\right)=\left\{u:{\Vert u\Vert }_{L([a,b])}={\displaystyle {\int }_a^b\left|x\left(t\right)\right|\text{d}t}<\infty \right\}.$

定义2.1 ( [8] [9] )：设 $x\left(t\right)$ 是定义在 $\left[0,T\right]$ 上的实值函数，其q阶Riemann-Liouville Tempered分数阶导数定义为

${}_a{D}_t^{q,\lambda }x\left(t\right)={\text{e}}^{-\lambda t}{}_{a}D{}_t^q\left({\text{e}}^{\lambda t}x\left(t\right)\right)=\frac{{\text{e}}^{-\lambda t}}{\Gamma \left(1-q\right)}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_t^a\frac{{\text{e}}^{\lambda s}x\left(s\right)}{{\left(t-s\right)}^q}\text{d}s},$ (2.1)

其中 ${}_a{D}_t^q\left({\text{e}}^{\lambda t}x\left(t\right)\right)$ 为Riemann-Liouville分数阶导数定义 [5]

${}_a{D}_t^q\left({\text{e}}^{\lambda t}x\left(t\right)\right)=\frac{\text{d}}{\text{d}t}\left({}_a{I}_t^{1-q}\left({\text{e}}^{\lambda t}x\left(t\right)\right)\right)=\frac{1}{\Gamma \left(1-q\right)}\frac{\text{d}}{\text{d}t}{\displaystyle {\int }_a^t\frac{\left({\text{e}}^{\lambda s}x\left(s\right)\right)}{{(t-s)}^{\alpha }}\text{d}s.}$ (2.2)

为了证明定理1.1，还需以下引理，有兴趣的读者可参考文献 [10] 中引理1的证明。

引理2.2

$\{\begin{array}{l}{}_a{D}_t^{q,\lambda }x\left(t\right)=f\left(t,x\left(t\right)\right),0<q<1,\lambda \ge 0\\ {\left[{}_a{D}_t^{q-1}\left({\text{e}}^{\lambda t}x\left(t\right)\right)\right]|}_{t=a}=g^0\end{array}$ (2.3)

若函数 $f\left(t,x\left(t\right)\right)$ 和 $x\left(t\right)$ 属于 $L\left(\left[a,b\right]\right)$ ， $x\left(t\right)$ 是柯西问题(2.3)的解，问题(2.3)等价Volterra积分方程：

$x\left(t\right)=g^0\frac{{\text{e}}^{-\lambda t}{\left(t-a\right)}^{q-1}}{\Gamma \left(q\right)}+\frac{1}{\Gamma \left(q\right)}{\displaystyle {\int }_a^t{\text{e}}^{-\lambda (t-s)}}{\left(t-s\right)}^{q-1}f\left(s,x\left(s\right)\right)\text{d}s.$

3. 主要结果及证明

在上述定义和引理的基础上，本文考虑分数阶微分方程(2.1)迭代近似值的唯一性和收敛性。

$\{\begin{array}{l}{D}^{q,\lambda }x\left(t\right)=f\left(t,x\left(t\right)\right),f\in C\left(R_0,R\right)\\ x\left(t_0\right)={x\left(t\right){\left(t-t_0\right)}^{1-q}|}_{t=t_0}=x^0\end{array}$ (3.1)

其中 $R_0=\left\{\left(t,x\right),t_0\le t\le t_0+a,\left|x-x^0\left(t\right)\right|\le b\right\}$ 和 $D^{q,\lambda }$ 表示为q阶Riemann-Liouville Tempered分数阶导数(见定义2.1)。由引理2.1可知柯西问题(3.1)等价于第二类Volterra积分方程：

$x\left(t\right)=x^0\left(t\right)+\frac{1}{\Gamma \left(q\right)}{\displaystyle {\int }_{t_0}^t{\text{e}}^{-\lambda (t-s)}}{\left(t-s\right)}^{q-1}f\left(s,x\left(s\right)\right)\text{d}s，$ (3.2)

其中 $x^0\left(t\right)=x^0\frac{{\text{e}}^{-\lambda t}{\left(t-t_0\right)}^{q-1}}{\Gamma \left(q\right)}$ 。因此(3.1)初值问题的每个解等价于(3.2) Volterra积分方程的解，反之亦然。

我们将推广到Tempered分数阶微分方程(3.1) Nagumo型解的存在性与唯一性。

定理3.1假设函数 $x\left(t\right)\in C_p\left(\left[t_0,t_0+a\right],R\right)=\left\{u:u\in C\left(\left[t_0,t_0+a\right],R\right)\right\}$ 是柯西问题(3.1)的一个解， ${\left(t-t_0\right)}^{p}u\left(t\right)\in C\left(\left[t_0,t_0+a\right],R\right),p=1-q$ 和 $D^{q,\lambda }$ 在区间 $\left[t_0,t_0+a\right]$ 内有意义且连续。那么假设(3.1)中f满足Nagumo条件：

$\left|f\left(t,x\right)-f\left(t,y\right)\right|\le \frac{\left|x-y\right|\Gamma \left(q\right)}{{\left(t-t_0\right)}^q},t\ne t_0,\left(t,x\right)\in R_0.$ (3.3)

那么迭代近似值

$x_{n+1}=x^0\left(t\right)+\frac{1}{\Gamma \left(q\right)}{\displaystyle {\int }_{t_0}^t{\text{e}}^{-\lambda (t-s)}}{\left(t-s\right)}^{q-1}f\left(s,x_n\left(s\right)\right)\text{d}s$ (3.4)

收敛于(3.1)在 $\left[t_0,t_0+\eta \right]$ 的唯一解 $x\left(t\right)$ ，其中 $\eta =\min {\left(a,\left(\frac{b\Gamma \left(1+q\right)}{M}\right)\right)}^{\frac{1}{q}}$ ，在 $R_0$ 上 $\left|f\left(t,x\right)\right|\le M$ 。

证明：第一步，要证(3.1)解 $x\left(t\right)$ 的唯一性。首先假设 $x\left(t\right),y\left(t\right)$ 是(3.1)的解。那么 $\varphi \left(t\right)=\left|x\left(t\right)-y\left(t\right)\right|$ 。因为 $\varphi \left(t_0\right)=0$ ，可得

$\begin{array}{c}\underset{t\to t_0^{+}}{\lim }\frac{\varphi \left(t\right)}{t-t_0}=\underset{t\to t_0^{+}}{\lim }\left(\frac{1}{t-t_0}\frac{1}{\Gamma \left(q\right)}{\displaystyle {\int }_{t_0}^t{\text{e}}^{-\lambda (t-s)}}{\left(t-s\right)}^{q-1}\left[f\left(s,x\left(s\right)\right)-f\left(s,y\left(s\right)\right)\right]\text{d}s\right)\\ =\frac{1}{\Gamma \left(q\right)}\left[{\left(t-t_0\right)}^{q-1}{\text{e}}^{-\lambda (t-t_0)}\left[f\left(t_0,x\left(t_0\right)\right)-f\left(t_0,y\left(t_0\right)\right)\right]\right]=0.\end{array}$ (3.5)

故而

$\underset{t\to t_0^{+}}{\lim }\frac{\varphi \left(t\right)}{{\left(t-t_0\right)}^q}{\text{e}}^{-\lambda (t-t_0)}=\underset{t\to t_0^{+}}{\lim }\frac{\varphi \left(t\right)}{\left(t-t_0\right)}\frac{{\left(t-t_0\right)}^{1-q}}{{\text{e}}^{\lambda (t-t_0)}}=0.$ (3.6)

接着使用Nagumo (3.3)条件得

$\varphi \left(t\right)\le \frac{1}{\Gamma \left(q\right)}{\displaystyle {\int }_{t_0}^t\frac{{\left(t-s\right)}^{q-1}{\text{e}}^{-\lambda (t-s)}\left|\varphi \left(s\right)\right|}{{\left(s-t_0\right)}^q}\text{d}s\Gamma \left(q\right)q}.$ (3.7)

令 $\frac{\varphi \left(t\right){\text{e}}^{-\lambda (t-t_0)}}{{\left(t-t_0\right)}^q}=\psi \left(t\right)$ ，同样地 $\psi \left(t_0\right)=0$ ，(3.7)可转化为

$\psi \left(t\right)\le \frac{q}{{\left(t-t_0\right)}^q}{\displaystyle {\int }_{t_0}^t{\left(t-s\right)}^q}\psi \left(s\right)\text{d}s.$

为了证(3.1)解的唯一性，等价于证明

$\psi \left(t\right)\equiv 0.$ (3.8)

令(3.8)不成立，则存在一点 $t_1\in \left(t_0,t_0+\eta \right)$ ，使得 $m=\underset{[t_0,t_0+\eta ]}{\max }\psi \left(t\right)=\psi \left(t_1\right)$ 。

那么

$\begin{array}{c}m=\psi \left(t_1\right)\\ \le \frac{q{\text{e}}^{-\lambda (t_1-t_0)}}{{\left(t_1-t_0\right)}^q}{\displaystyle {\int }_{t_0}^{t_1}{\left(t_1-s\right)}^q}\psi \left(s\right)\text{d}s\\ <\frac{qm}{{\left(t_1-t_0\right)}^q}{\displaystyle {\int }_{t_0}^{t_1}{\left(t_1-s\right)}^q}\text{d}s\\ ={\frac{qm}{{\left(t_1-t_0\right)}^q}\frac{{\left(t_1-s\right)}^q}{-q}|}_{t_0}^{t_1}\\ =\frac{qm}{{\left(t_1-t_0\right)}^q}\frac{{\left(t_1-t_0\right)}^q}{q}=m.\end{array}$ (3.9)

这证得了 $\psi \left(t\right)\equiv 0$ ，意味着 $\varphi \left(t\right)\equiv 0$ ，即(3.1)柯西问题有唯一解。

现在我们要证逐次近似值 $x_{n+1}\left(t\right)$ ， $n=0,1,2,\cdots$ 满足：

(i) 是良定义和连续的；

(ii) 是一致有界的；

(iii) 在 $\left[t_0,t_0+\eta \right]$ 上等度连续的。

其中 $\eta =\min {\left(a,\left(\frac{b\Gamma \left(1+q\right)}{M}\right)\right)}^{\frac{1}{q}}$ ，以及在 $R_0$ 上 $\left|f\left(t,x\right)\right|\le M$ 。

现在由(3.4)的定义可知，

$\left|x_{n+1}\left(t\right)-x^0\left(t\right)\right|\le {\displaystyle {\int }_{t_0}^t{\left(t-s\right)}^{q-1}}\left|f\left(x,x_n\left(s\right)\right)\right|{\text{e}}^{-\lambda (t-s)}\text{d}s.$

当 $n=0$ 时，结合 $\left|f\left(t,x\right)\right|\le M$ 上式可化为

$\left|x_1\left(t\right)-x^0\left(t\right)\right|\le {\frac{CM}{\Gamma \left(q\right)}\frac{{\left(t-s\right)}^q}{-q}|}_{t_0}^t=\frac{CM{\left(t-t_0\right)}^q}{q\Gamma \left(q\right)}=\frac{CM{a}^q}{q\Gamma \left(q\right)}\le b$

其中C是常数。

通过数学归纳法可得 $\left\{x_{n+1}\left(t\right)\right\}$ 符合(ii)条件，即函数族 $\left\{x_{n+1}\left(t\right)\right\}$ 在 $\left[t_0,t_0+\eta \right]$ 是一致有界的。

对于 $t_0\le t_1\le t_2$ ，结合 $x_n\left(t\right)$ 的定义和 $\left|f\left(t,x\right)\right|\le M$ ，我们有

$\begin{array}{c}\left|x_n\left(t_1\right)-x_n\left(t_2\right)\right|\\ \le \frac{1}{\Gamma \left(q\right)}\left[\left|{\displaystyle {\int }_{t_0}^{t_1}{\left(t_1-s\right)}^{q-1}}{\text{e}}^{-\lambda (t_1-s)}f\left(s,x_n\left(s\right)\right)ds-{\displaystyle {\int }_{t_0}^{t_2}{\left(t_2-s\right)}^{q-1}}{e}^{-\lambda (t_2-s)}f\left(s,x_n\left(s\right)\right)ds\right|\right]\\ =\frac{1}{\Gamma \left(q\right)}\left[\left|{\displaystyle {\int }_{t_0}^{t_1}\left({\left(t_1-s\right)}^{q-1}{\text{e}}^{-\lambda (t_1-s)}-{\left(t_2-s\right)}^{q-1}{\text{e}}^{-\lambda (t_2-s)}\right)f\left(s,x_n\left(s\right)\right)\text{d}s}-{\displaystyle {\int }_{t_1}^{t_2}{\left(t_2-s\right)}^{q-1}}{\text{e}}^{-\lambda (t_2-s)}f\left(s,x_n\left(s\right)\right)\text{d}s\right|\right]\end{array}$

$\begin{array}{c}\le \frac{M}{\Gamma \left(q\right)}\left[{\displaystyle {\int }_{t_0}^{t_1}\left({\left(t_1-s\right)}^{q-1}-{\left(t_2-s\right)}^{q-1}\right)\text{d}s}+{\displaystyle {\int }_{t_1}^{t_2}{\left(t_2-s\right)}^{q-1}}\text{d}s\right]\\ =\frac{M}{\Gamma \left(q+1\right)}\left[{\left(t_1-t_0\right)}^q-{\left(t_2-t_0\right)}^q+2{\left(t_2-t_1\right)}^q\right]\\ \le \frac{2M}{\Gamma \left(q+1\right)}{\left(t_2-t_1\right)}^q.\end{array}$ (3.10)

若 $\left|t_2-t_1\right|<\delta ={\left(\frac{ϵ\Gamma \left(q+1\right)}{2M}\right)}^{\frac{1}{q}}$ ，对于n足够大，则(3.10)满足小于 $ϵ$ ，即

$\left|x_n\left(t_1\right)-x_n\left(t_2\right)\right|<ϵ.$

故而容易得函数族 $\left\{x_{n+1}\left(t\right)\right\}$ 在 $\left[t_0,t_0+\eta \right]$ 是等度连续的，因此存在一致收敛的子列 $\left\{x_{n_k}\left(t\right)\right\}$ 。于是，假设当 $n\to \infty$ 时， $\left\{x_n\left(t\right)-x_{n+1}\left(t\right)\right\}\to 0$ ，则(3.4)说明任何这样的子列的极限都是(3.1)的唯一解 $x\left(t\right)$ 。在此基础上，由文献 [4] 可知选择一个子列是不必要的，并且完整的序列 $x_{n+1}\left(t\right)$ 一致收敛于 $x\left(t\right)$ 。因此，我们可以得到

$\varphi \left(t\right)=\underset{n\to \infty }{\lim \sup }\left(\left|x_{n+1}\left(t\right)-x_n\left(t\right)\right|\right)\equiv 0.$ (3.11)

对于 $t_0\le t_3\le t_4$ ，同理可得：

$\begin{array}{c}\left|x_n\left(t_3\right)-x_{n-1}\left(t_3\right)\right|-\left|x_n\left(t_4\right)-x_{n-1}\left(t_4\right)\right|\\ \le \left|x_n\left(t_3\right)-x_{n-1}\left(t_3\right)-x_n\left(t_4\right)+x_{n-1}\left(t_4\right)\right|\\ \le \frac{1}{\Gamma \left(q\right)}\left[\left|{\displaystyle {\int }_{t_0}^{t_3}{\left(t_3-s\right)}^{q-1}}{\text{e}}^{-\lambda (t_3-s)}D\left(S\right)\text{d}s-{\displaystyle {\int }_{t_0}^{t_4}{\left(t_4-s\right)}^{q-1}}{\text{e}}^{-\lambda (t_4-s)}D\left(S\right)\text{d}s\right|\right]\\ =\frac{1}{\Gamma \left(q\right)}\left[\left|{\displaystyle {\int }_{t_0}^{t_3}\left({\left(t_3-s\right)}^{q-1}{\text{e}}^{-\lambda (t_3-s)}-{\left(t_4-s\right)}^{q-1}{\text{e}}^{-\lambda (t_4-s)}\right)D\left(s\right)\text{d}s}-{\displaystyle {\int }_{t_3}^{t_4}{\left(t_4-s\right)}^{q-1}}{\text{e}}^{-\lambda (t_4-s)}D\left(s\right)\text{d}s\right|\right]\end{array}$

$\begin{array}{c}\le \frac{2M}{\Gamma \left(q\right)}\left[{\displaystyle {\int }_{t_0}^{t_3}\left({\left(t_3-s\right)}^{q-1}-{\left(t_4-s\right)}^{q-1}\right)\text{d}s}+{\displaystyle {\int }_{t_3}^{t_4}{\left(t_4-s\right)}^{q-1}}\text{d}s\right]\\ =\frac{2M}{\Gamma \left(q+1\right)}\left[{\left(t_3-t_0\right)}^q-{\left(t_4-t_0\right)}^q+2{\left(t_4-t_3\right)}^q\right]\\ \le \frac{4M}{\Gamma \left(q+1\right)}{\left(t_4-t_3\right)}^q.\end{array}$ (3.12)

其中在 $R_0$ 上 $\left|D\left(s\right)\right|=\left|f\left(s,x_{n-1}\left(s\right)\right)-f\left(s,x_{n-2}\left(t\right)\right)\right|\le 2M$ ，以及 $x_n\left(t\right)$ 与(3.4)中定义相同。

若 $\left|t_4-t_3\right|<\delta ={\left(\frac{ϵ\Gamma \left(q+1\right)}{4M}\right)}^{\frac{1}{q}}$ ，则(3.12)满足小于 $ϵ$ 。对于n足够大， $ϵ>0$ ，(3.12)可化为

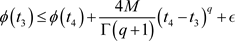
因为 $t_3,t_4$ 可任意替换，以及 $ϵ>0$ 是任意，故而

$\left|\varphi \left(t_3\right)-\varphi \left(t_4\right)\right|\le \frac{4M}{\Gamma \left(q+1\right)}{\left(t_4-t_3\right)}^q.$

由此证得 $\varphi \left(t\right)$ 的连续性。

接下来，结合Nagumo条件和(3.4)中 $x_{n+1}\left(t\right)$ 的定义，可得

$\left|x_{n+1}\left(t\right)-x_n\left(t\right)\right|\le \frac{q\Gamma \left(q\right)}{\Gamma \left(q\right)}{\displaystyle {\int }_{t_0}^t{\left(t-s\right)}^{q-1}}{\text{e}}^{-\lambda (t-s)}\frac{\left|x_n\left(s\right)-x_{n-1}\left(s\right)\right|}{{\left(s-t_0\right)}^q}\text{d}s$ (3.13)

任意固定 $t\in \left[t_0,t_0+\eta \right]$ ，则存在一个整数序列 $n_1<n_2<\cdots$ ，使得当 $n=n_k\to \infty$ ，

$\left|x_{n+1}\left(t\right)-x_n\left(t\right)\right|\to \varphi (\; t\; )$

和 ${\varphi }^{*}\left(t\right)=\underset{n=n_k\to \infty }{\lim }\left|x_n\left(t\right)-x_{n-1}\left(t\right)\right|$ 一致存在于 $t\in \left[t_0,t_0+\eta \right]$ 。

因此，

$\varphi \left(t\right)\le q{\displaystyle {\int }_{t_0}^t{\left(t-s\right)}^{q-1}}{\text{e}}^{-\lambda (t-s)}\frac{{\varphi }^{*}\left(t\right)}{{\left(s-t_0\right)}^q}\text{d}s.$ (3.14)

由于 ${\varphi }^{*}\left(t\right)\le \varphi \left(t\right)$ ，(3.14)放缩为

$\varphi \left(t\right)\le q{\displaystyle {\int }_{t_0}^t{\left(t-s\right)}^{q-1}}{\text{e}}^{-\lambda (t-s)}\frac{\varphi \left(t\right)}{{\left(s-t_0\right)}^q}\text{d}s.$ (3.15)

与上文证明相似，我们可以得出

$\begin{array}{c}\underset{t\to t_0^{+}}{\lim }\frac{\varphi \left(t\right)}{t-t_0}=\underset{t\to t_0^{+}}{\lim }\left(\frac{1}{t-t_0}\frac{1}{\Gamma \left(q\right)}{\displaystyle {\int }_{t_0}^t{\text{e}}^{-\lambda (t-s)}}{\left(t-s\right)}^{q-1}\left[f\left(s,x_n\left(s\right)\right)-f\left(s,x_{n-1}\left(s\right)\right)\right]\text{d}s\right)\\ =\frac{1}{\Gamma \left(q\right)}\left[{\left(t-t_0\right)}^{q-1}{\text{e}}^{-\lambda (t-t_0)}\left[f\left(t_0,x_n\left(t_0\right)\right)-f\left(t_0,x_{n-1}\left(t_0\right)\right)\right]\right]=0.\end{array}$

更进一步可得，

$\underset{t\to t_0^{+}}{\lim }\frac{\varphi \left(t\right)}{{\left(t-t_0\right)}^q}{\text{e}}^{-\lambda (t-t_0)}=\underset{t\to t_0^{+}}{\lim }\frac{\varphi \left(t\right)}{\left(t-t_0\right)}\frac{{\left(t-t_0\right)}^{1-q}}{{\text{e}}^{\lambda (t-t_0)}}=0.$

假设 $\psi \left(t\right)=\frac{\varphi \left(t\right)}{{\left(t-t_0\right)}^q}{\text{e}}^{-\lambda (t-t_0)}$ ，从上式可得 $\psi \left(t_0\right)=0$ 。接下来，为了证 $x_{n+1}\left(t\right)$ 的收敛性，等价于证

$\psi \left(t\right)\equiv 0.$ (3.16)

假设(3.16)不成立，则存在 $\psi \left(t_1\right)=\underset{\left[t_0,t_0+\eta \right]}{\max }\psi \left(t\right)=m$ 。那么

$\begin{array}{c}m=\psi \left(t_1\right)=\frac{\varphi \left(t_1\right)}{{\left(t_1-t_0\right)}^q}{\text{e}}^{-\lambda (t_1-t_0)}\le \frac{q{\text{e}}^{-\lambda (t_1-t_0)}}{{\left(t_1-t_0\right)}^q}{\displaystyle {\int }_{t_0}^{t_1}{\left(t_1-s\right)}^q}\psi \left(s\right)\text{d}s\\ <\frac{qm}{{\left(t_1-t_0\right)}^q}{\displaystyle {\int }_{t_0}^{t_1}{\left(t_1-s\right)}^q}\text{d}s\\ ={\frac{qm}{{\left(t_1-t_0\right)}^q}\frac{{\left(t_1-s\right)}^q}{-q}|}_{t_0}^{t_1}\\ =\frac{qm}{{\left(t_1-t_0\right)}^q}\frac{{\left(t_1-t_0\right)}^q}{q}=m.\end{array}$ (3.17)

显然矛盾，(3.16)成立，即逐次近似值 $x_{n+1}\left(t\right)$ (见(3.4))收敛于(3.1)的唯一解。定理3.1成立。