支座平移法的有效性和局限性

The Effectiveness and Limitation of Support Translation Method

摘要: 基于铰结三角形的几何不变性可衍生出系列判别规则，是现有教材中几何组成分析的主要教学内容。但实际问题复杂多变，几何法或将难以处理，其它各类分析方法便应运而生。作为结构力学的经典方法，支座平移法常用于几何组成分析中。根据典型算例，应用支座平移法和解析法分析体系的几何组成性质，并将分析结果与结构力学求解器的计算结果进行对比分析。结果表明：支座沿链杆作用方向平移，不改变约束的性质，支座平移是有效的，可应用支座平移法分析体系的几何组成性质，其它情况进行支座平移或将导致错误的结果。因此，支座平移法有适用性和局限性，在结构力学教学中需慎重使用。

Abstract: Based on the geometric invariance of hinged triangle, a series of discriminant rules can be derived, which is the main teaching content of geometric composition analysis in existing textbooks. However, the practical problems are complex and changeable, and the geometric method may be difficult to deal with. Therefore, other kinds of analysis methods emerge as the times require. As the classical method of Structural Mechanics, the support translation method is often used in geometric composition analysis. According to the typical example, the support translation method and the analytical method are used to analyze the geometric composition of the system, and the analysis results are compared with the calculation results of the structural mechanics solver. The results show that the translation of the support along the axial direction of the hinged bar does not change the nature of the constraint, and the translation is effective. Here, the geometric composition of the system can be analyzed by the support translation method. In other cases, the translation of the support may lead to wrong results. Therefore, the support translation method has applicability and limitations, which should be used conditionally in the teaching of Structural Mechanics.

1. 引言

若干个杆件以某种方式相互连接，则构成杆件体系。按照几何学的原理对体系发生运动的可能性进行分析，称为体系的几何构造分析，亦可称为几何组成分析 [1] 。平面杆系的几何组成分析是结构力学的重要教学内容，现有结构力学教材主要讲授基于铰结三角形的几何法，有3个基本规则：两刚片规则、三刚片规则和二元体规则。静力法也常用于分析体系的几何组成性质，如零载法等 [2] [3] 。

几何法和零载法的灵活应用可解决大部分平面体系的几何组成分析问题，但对于一些复杂问题，这些方法应用不便。应用支座平移法可将复杂体系简化为关系清晰、组成简单的体系，可用于分析体系的几何组成性质 [4] 。支座移动到与其轴线重合的一根直杆或多个铰接共线直杆上的任意不与其它轴向约束重合的位置，体系的几何构造分析结论不变 [5] 。但实际上，支座平移法有局限性，不当的支座平移将导致错误的结果。另外，等效代换法 [6] [7] [8] [9] 、解析法 [10] 等方法也常用于分析体系的几何组成性质。

本文选用文献 [4] 中的典型算例4，分别应用支座平移法和解析法分析、求解，并结合结构力学求解器 [11] 的计算结果，探讨支座平移法的有效性和局限性。

2. 支座平移法

支座平移法：在地基必须视为刚片的体系中，如不存在杆身共线或通过地基铰的支承链杆，则连接于铰接三角形二杆结点处的地基铰或支承链杆可平移到这二杆另端无支承的结点处。但需注意，在每一次支座平移后，体系中均不允许出现杆身共线或通过地基铰的支承链杆，也不允许出现三实铰(其中含二个地基铰)共线的情形 [4] 。

算例：试分析图1所示体系的几何组成。

Figure 1. Plane bar system

图1. 平面杆系

文献 [4] 的解法如下：利用支座平移法将1、2、3、4处的支承链杆分别平移至5、6、7、8，再分别撤除二元体，可得简化的等效体系，如图2所示。选58杆、67杆、基础分别为刚片I、刚片II、刚片III，刚片I和刚片II由链杆56、链杆78组成的无穷远虚铰相联，刚片II和刚片III由虚铰7相联，刚片I和刚片III由虚铰5相联，三铰不共线，故体系为无多余约束的几何不变体。

Figure 2. Simplified system

图2. 简化体系

1处的水平支座链杆平移到5点，2处的竖向支座链杆平移到6点，3处的水平支座链杆平移到7点，4处的竖向支座链杆平移到8点。4根支座链杆均没有沿链杆作用线方向平移，或许改变了约束的性质，“无多余约束的几何不变体”的结论有待验证。

3. 解析法

根据几何组成分析时杆单元为刚性单元的特点，确定杆端位移在平面内满足的约束方程，应用解析法判断体系的几何组成性质 [10] 。根据体系的约束特点，采用先处理法形成结点和单元定位向量，可以有效减少体系的总结点位移个数。将文献 [4] 中的算例稍加调整，如图3所示。

Figure 3. Number of plane bar system

图3. 平面杆系的编号

平面体系中所有杆件均为链杆，故只需考虑杆端的线位移。为了减少计算量，应用先处理法对体系进行结点、单元和结点位移编号，如图3所示。其中，结点1、结点2、结点3和结点4在进行位移编号时已考虑支座约束，结点5、结点6、结点7和结点8在进行位移编号时已考虑水平链杆和竖向链杆的轴向约束。体系暂未考虑单元(1)、单元(2)、单元(3)、单元(4)共4根斜链杆的约束条件，下面将单独讨论。

单元定位向量

$\begin{array}{c}(1)\\ (2)\\ (3)\\ (4)\end{array}\left[\begin{array}{cc}1& 6\\ 7& 2\\ 8& 3\\ 4& 5\end{array}\right]\begin{array}{c}\end{array}\left[\begin{array}{cccc}0& 1& 2& 3\\ 4& 3& 2& 0\\ 4& 1& 0& 3\\ 4& 0& 2& 1\end{array}\right]$ (1)

单元(1)的约束方程

${\Delta }_1\cos {\theta }_1=-{\Delta }_2\sin {\theta }_1+{\Delta }_3\cos {\theta }_1$ (2)

单元(2)的约束方程

${\Delta }_2\cos {\theta }_2={\Delta }_3\sin {\theta }_2+{\Delta }_4\cos {\theta }_2$ (3)

单元(3)的约束方程

${\Delta }_1\cos {\theta }_3-{\Delta }_4\sin {\theta }_3\text{=}{\Delta }_3\cos {\theta }_3$ (4)

单元(4)的约束方程

${\Delta }_4\cos {\theta }_4\text{=}{\Delta }_1\sin {\theta }_4+{\Delta }_2\cos {\theta }_4$ (5)

将式(2)~式(5)共4个方程联立，其矩阵形式为

$\left[\begin{array}{cccc}\cos {\theta }_1& \sin {\theta }_1& -\cos {\theta }_1& 0\\ 0& \cos {\theta }_2& -\sin {\theta }_2& -\cos {\theta }_2\\ \cos {\theta }_3& 0& -\cos {\theta }_3& -\sin {\theta }_3\\ \sin {\theta }_4& \cos {\theta }_4& 0& -\cos {\theta }_4\end{array}\right]\cdot \left[\begin{array}{c}{\Delta }_1\\ {\Delta }_2\\ {\Delta }_3\\ {\Delta }_4\end{array}\right]=0$ (6)

则，约束方程的系数矩阵为

$G=\left[\begin{array}{cccc}\cos {\theta }_1& \sin {\theta }_1& -\cos {\theta }_1& 0\\ 0& \cos {\theta }_2& -\sin {\theta }_2& -\cos {\theta }_2\\ \cos {\theta }_3& 0& -\cos {\theta }_3& -\sin {\theta }_3\\ \sin {\theta }_4& \cos {\theta }_4& 0& -\cos {\theta }_4\end{array}\right]$ (7)

若 $\left|G\right|\ne 0$ ，则 ${\Delta }_1={\Delta }_2={\Delta }_3={\Delta }_4=0$ ，体系几何不变，且无多余约束；若 $\left|G\right|=0$ ，则体系几何可变。

讨论：1)取 ${\theta }_1={\theta }_2={\theta }_3={\theta }_4=45°$ ，即 $\sin \theta =\cos \theta =\sqrt{2}/2$ ，则 $\left|G\right|\ne 0$ ，体系几何不变，且无多余约束；2)取 ${\theta }_1={\theta }_2={\theta }_3={\theta }_4=63.435°$ ，即 $\sin \theta =2/\sqrt{5}$ ， $\cos \theta =1/\sqrt{5}$ ，此时图3体系与图1体系完全相同，经计算 $\left|G\right|=0$ ，故体系几何可变，与支座平移法结论不同。

应用结构力学求解器 [11] 进行分析，图1体系为几何可变体系，也与支座平移法结论不同。改变体系的几何尺寸，结构力学求解器的分析结果与解析法完全相同。

4. 支座平移法的有效性

改变图3中结点1、结点2、结点3和结点4的支座链杆方向，将4个支座链杆均顺时针转置90度，研究支座平移法的有效性。应用先处理法对体系进行结点、单元和结点位移编号，如图4所示。其中，结点1、结点2、结点3和结点4在进行位移编号时已考虑支座约束，结点5、结点6、结点7和结点8在进行位移编号时已考虑水平链杆和竖向链杆的轴向约束。很明显，当不考虑链杆的轴向变形时，结点5、结点6、结点7和结点8没有任何线位移。体系暂未考虑单元(1)、单元(2)、单元(3)、单元(4)共4根斜链杆的约束条件，下面将单独讨论。

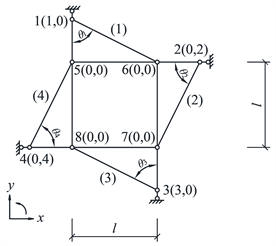
Figure 4. Number of modified plane bar system

图4. 修改后平面杆系的编号

单元(1)的约束方程

${\Delta }_1\sin {\theta }_1=0$ (8)

单元(2)的约束方程

${\Delta }_2\sin {\theta }_2=0$ (9)

单元(3)的约束方程

${\Delta }_3\sin {\theta }_3\text{=}0$ (10)

单元(4)的约束方程

${\Delta }_4\sin {\theta }_4\text{=}0$ (11)

将式(8)~式(11)共4个方程联立，其矩阵形式为

$\left[\begin{array}{cccc}\sin {\theta }_1& 0& 0& 0\\ 0& \sin {\theta }_2& 0& 0\\ 0& 0& \sin {\theta }_3& 0\\ 0& 0& 0& \sin {\theta }_4\end{array}\right]\cdot \left[\begin{array}{c}{\Delta }_1\\ {\Delta }_2\\ {\Delta }_3\\ {\Delta }_4\end{array}\right]=0$ (12)

则，约束方程的系数矩阵为

$G=\left[\begin{array}{cccc}\sin {\theta }_1& 0& 0& 0\\ 0& \sin {\theta }_2& 0& 0\\ 0& 0& \sin {\theta }_3& 0\\ 0& 0& 0& \sin {\theta }_4\end{array}\right]$ (13)

只要 $\theta \ne 0$ ，则 $\left|G\right|\ne 0$ ，可得 ${\Delta }_1={\Delta }_2={\Delta }_3={\Delta }_4=0$ ，体系几何不变，且无多余约束。

应用支座平移法，将图4简化为图5所示体系。取杆58、杆67和基础分别为3个刚片，应用三刚片规则，易导出原体系为无多余约束的几何不变体。应用结构力学求解器分析，得出的结论与解析法和支座平移法相同。此种情况下，支座平移法是有效的。

Figure 5. Modified simplified system

图5. 修改后的简化体系

因此，当支座链杆沿着链杆方向移动，比如结点1处的竖向链杆支座沿着竖直方向的杆15移动到结点5时，不改变体系的约束性质，可用支座平移法分析体系的几何组成。

5. 结论

支座平移法可将复杂问题简单化，常用于结构力学教学中，深受广大师生的喜爱。但是，支座平移法有适用范围，不正确的支座平移将改变约束的性质，会导致错误的结论。若支座沿链杆作用方向移动，不改变约束性质，可应用支座平移法；否则，不能用支座平移法。因此，支座平移法有局限性和适用性，在结构力学教学中需慎重使用。

基金项目

陕西省自然科学基础研究计划(2023-JC-YB-435)，教学改革研究专项(JGZ220110)。