1. 引言
种群是生态学最基本的单位之一,具有许多不同于个体的特征。它也是生物群落结构和功能的最基本单位。许多与环境有关的生物变化都发生在这一层次,它也是物种适应的基础单位。此外,对种群进化过程的研究一直是学术界研究的热点。自达尔文提出自然选择理论 [1] 以来,许多学者对种群的进化过程进行了进一步的研究。第一个是孟德尔的遗传理论 [2] ,它为20世纪研究遗传原理打开了大门。后来,R. Fisher,J. B. Haldane和S. Wright [3] [4] 将孟德尔的遗传理论与达尔文的进化理论结合起来,创造了新的种群遗传学学科。他们的理论在研究生物进化机制,特别是种内进化机制方面发挥了重要作用。在现代,对种群进化的研究在深度和复杂性上都有所增加。随着计算机技术的发展,人们提出了许多进化算法。粒子群优化(PSO)算法 [5] [6] 就是这样一种进化计算技术。它的原理是基于对动物群体活动的观察,以及群体中的个体如何利用信息共享来推动整个群体在问题解决空间中的移动。这创造了一个从无序到最佳解决方案的进化过程。然而,利用类似粒子群算法的进化算法来分析博弈论中的种群进化的研究却很少。
在博弈论的背景下,许多学者从不同的角度探讨了种群进化的过程。研究视角的探索可分为三个主要阶段。第一阶段是进化博弈的诞生阶段,对种群进化表现出极大的兴趣 [7] [8] [9] [10] 。一些学者运用博弈论的框架和进化稳定性的思想来分析种群进化的结果。他们认为,整个进化过程很可能会落入一个不再波动的稳定点;这被称为进化稳定点。其中,研究重点是进化稳定策略的本质。如Smith和Price [7] 基于博弈论提出,个体之间的竞争导致整个种群状态不断变化,但最终达到一个稳定的竞争点,这个稳定点就是进化稳定策略。刘奇龙等 [8] 基于经典的鹰鸽博弈模型,同时考虑非对称性相互关系和资源压力的影响,建立了具有强弱之分的四策略非对称博弈模型。
第二阶段,随着复制动力学方程的引入,一些学者开始从动力学角度研究种群进化 [11] - [17] 。他们认为种群的进化遵循动力学中的复制动力学方程,该方程的解代表了进化轨迹。例如,Weibull [12] 利用复制动力学方程分析了经典种群博弈模型,如鹰鸽博弈,得到了它们的复制子动力学图,并推导出了它们的稳定进化策略。梅杰等 [14] 将进化博弈动力学引入有限种群,研究弱选择机制对进化过程和结果的影响。
第三阶段,提出了一系列基于生物优点搜索的进化算法,如粒子群算法、遗传算法、进化多目标算法等。由于这些算法来源于生物体中的一些进化现象,因此它们非常适合于这些现象的研究 [18] - [23] 。例如Birchenhall [18] 分析了种群进化过程与遗传算法之间的共性,认为用遗传算法模拟种群进化过程是可行的。此外,Gupta等 [22] 基于植物遗传学的进化理论,结合传统算法,提出了一种二元编码进化算法,用于分析植物遗传学的进化过程。
本文的研究课题如下:1) 粒子群算法只能找到函数的极值点,用极值点来解决优化问题。基于成功行为的模仿和种群中策略的摄动现象,对粒子群算法进行了改进。粒子群优化算法解决了种群进化问题。2) 利用种群粒子群优化算法模拟了具有收益矩阵的单种群进化过程。进一步给出了进化稳定策略的实现路径。
本文利用粒子群优化算法模拟单个种群的进化过程,寻找其进化稳定点的路径。余下的论文组织如下。在第2节中,介绍了基本概念,然后在第3节中分析了PPSOs原则。第4节描述了PPSO的计算过程。第5节进行了仿真实验和单种群博弈分析。在第6节中,我们对变异进行了参数分析。本文在第七部分进行总结。
2. 问题描述
2.1. 粒子群优化算法
1995年,受群体觅食行为规律性的启发,James Kennedy和Russell Eberhart [6] 提出了一种简化的算法模型,经过多年的改进,最终形成了粒子群优化算法。粒子群算法的思想源于对鸟群觅食行为的研究,鸟群通过集体信息共享找到最优目的地。在粒子群算法中,每个优化问题的潜在解可以看作是d维搜索空间中的一个点,称为粒子。令第i个粒子记为
,速度为
,令其经历过的最佳位置(即适应度值最佳的位置)记为
,总体中所有粒子所经历的总体最佳位置也用上述符号表示。在每次迭代中,
和
根据以下公式变化:
式中,
和
分别是调节全局最佳粒子最大步长和特定最佳粒子飞行方向的学习因子;
和
为
范围内的随机数;w为惯性权重,通常按
计算,其中
和
分别为最大和最小惯性权重,
为最大迭代次数,k为当前迭代次数。
2.2. 决定种群进化的主要因素
在许多应用中,生物繁殖不能很好地描述某些行为如何在总体中传播和稳定。在社会科学和经济模型中,用模仿和学习成功行为的过程来描述行为扩散更为恰当,如( [10] , p. 125)所述。具体来说,在博弈论下,个体在群体中有不同的选择策略。基于混合策略单纯形形式Δ基和收益矩阵,单纯形是指包含所有策略选择的空间。单个种群中每个纯策略
所对应的总体份额增长率定义如下:
其中x为人口整体呈现的战略状态;
是个体选择纯策略i的概率,
是个体选择的第i个策略;
是个体选择纯策略i并且对手选择策略x时,从而得到的收益;
而是
的导数。
2.3. 进化稳定策略(单种群)
对于总体呈现策略状态为x的种群,设总种群中的个体采用(纯或混合)原始策略
。之后,一些个体的策略发生了变化,这些策略发生变化的个体被定义为突变体。没有策略变化的个体被定义为未突变个体。假设所有突变体均采用其他(纯或混合)突变策略
。突变体在总体中的份额表示为ε,其中
。在这个双峰总数中,随机重复抽取成对来进行博弈,每对被抽取的概率相同。因此,如果一个人被选中参加这个博弈,他的对手采用变异策略的概率是ε,而原策略的概率是
。这里我们假设收益符号为u,因此,原始策略的收益为
,而扰动策略的收益为
。如果相应个体的收益(适应度)高于选择变异策略的个体,进化将选择原始策略。具体情况如下:
在这种情况下,原始策略
被认为是进化稳定的,如果变体在总体中的份额足够小,则该不等式适用于任何变体策略
。
3. PPSO原理
3.1. 实现原理
在本文中,由于粒子群算法和进化博弈都是基于生物最优搜索的原理,我们做了如下的类比:
群体中的小群体→群体中的粒子;
策略空间→搜索空间;
行为扩散→迭代过程;
收益函数→收益函数;
最优收益→迭代最优收益;
进化稳定策略→迭代最优点。
因此,群体中所有个体策略的变化都类似于粒子对最优解的搜索。进化博弈的思想可以用来改进粒子群优化算法,使其在算法上模拟种群进化过程。考虑到混合策略粒子选择的合理性,假设总体由小群体组成,每个小群体集体选择策略。因此,在粒子群算法中,小群体可以看作是一个粒子,粒子可以采取混合策略。
3.2. 确定变量(对手的策略)
定理:在一个种群中,博弈对手的策略是由种群本身决定的。
证明:从2.3节中,假设一个总体有n个群体和m个可选策略。如果一个群体是随机选择的,那么它将与群体中的其他群体进行博弈,并且遇到任何其他群体的概率是相等的。这反映在策略选择上,表现为其他组的平均策略数。如果选择第i组参与博弈
,则其对手选择策略
的概率为其他组选择策略
的概率的平均值,即
其中
是选择第j个策略的小组;
表示该组对手选择策略j的概率,
表示第p个小组选择第q个策略的概率
。
补充:本文最后的仿真选择了一个经典的2 × 2博弈。在这类博弈模型中,从小组的策略是一个二维向量,各分量之和为1出发,策略的第二分量的值可以用第一分量的值来表示。也就是说,博弈方1只有一个变量,定义为适应度函数中的x。同样,对手的策略是一个二维向量,可以用一个变量表示,定义为适应度函数中的第二个变量y。因此,整个收益函数是二元的。
对于一个有收益矩阵的游戏
,第一方的收益为
3.3. 迭代方程(成功行为的模仿)
由公式3可知,当
时,
增大,说明部分群体倾向于选择策略i。当
时,
减小,说明部分最初选择策略i的群体会减少选择策略i的比例。由此可见,群体中的群体通过模仿成功的行为改变了策略选择。在这里,成功行为在收益层面表示为群体中收益最大所对应的策略选择。以有两种策略的单一种群为例,假设有10个群体,其中5个选择纯策略1,其余选择策略2。群体选择策略1的收益大于群体选择策略2的收益。然后,最初选择纯策略2的群体将进化为选择策略1的策略选择来模仿成功的行为。
为了使粒子模仿成功的行为,需要消除个体记忆对扩散行为的影响。消除单个内存意味着粒子不记得之前迭代的结果。迭代公式去掉群最优点,将全局最优点调整为迭代最优点。同时考虑了自然群体的行为惯性对策略选择的影响,因为行为惯性表示最后一次迭代的模仿。调整后的速度和位置更新方程如下:
其中,
表示在一次迭代中适应度值最优的粒子在种群中的位置。
3.4. 扰动变化
从第2.3节和公式4可以清楚地看出,模拟单个种群的进化必须包括群体将经历突变的情况。在PPSO中,一旦根据粒子间距离检测到粒子收敛,其中一些粒子被初始化为随机粒子,随机粒子是指系统在可行范围内随机生成粒子的位置。然后整个算法继续迭代,达到2.3节中变例的模拟。它的做法如下。
首先,将一组粒子初始化为随机粒子,每个粒子的策略组合为
。经过k次迭代,粒子的位置为
。
假设粒子收敛于以下情况:
,
然后,选择
个粒子成为随机粒子,继续迭代。在学习理论中,学习者在学习刚开始是为了寻找
更好的收益,会不合理地、剧烈地改变策略,这是在算法过程中观察到的变异现象。随着学习次数的增加,学习者的策略选择始终基于追求优势的原则,不再非理性地改变策略。考虑到这种情况,如果总迭
代次数为m,则突变过程只执行前
次迭代,之后不再执行。
4. PPSO计算过程
PPSO的实施步骤如下:
a) 首先确定PPSO的参数值。这些参数包括学习因子c、最大迭代次数
、最大和最小惯性权重
和
、最大和最小速度
和
、搜索空间中
和
的上下精确界限、总体大小n和变分精度
。
b) 第一个变量
随机生成n个粒子,其中
。初始化每个粒子的速度
,使
。
c) 第二个变量y的值根据公式5计算。然后,根据公式6计算每个粒子的适应度,找到粒子的迭代最优点
。
d) 惯性权重w按
计算,其中k为当前迭代次数。
e) 根据公式7更新粒子的速度,并进行边界检查以确保其位于
范围内。
f) 根据公式8更新粒子的位置,并应用边界检查以确保其位于
范围内。这确保了所有粒子都在它们的搜索空间内。
g) 判断在前
次中,粒子之间的距离是否符合公式9。如果是,继续下一步,否则转到步骤i)。
h) 对于第一个种群中的所有粒子:将
个粒子初始化为随机粒子。
i) 计算y的值,
的最大迭代次数按公式5,6计算。
j) 达到最大迭代次数,输出所有迭代的最优适应度值和粒子位置图。否则,算法返回到d)。
5. 仿真实验
为了评价TPPSO算法模拟两个种群进化过程的能力,选取了3个经典的2 × 2博弈(囚徒困境、协调博弈和鹰鸽博弈)作为算例,利用以下收益函数和计算结果,采用TPPSO算法求解。
囚徒困境:
,
,
协调博弈:
,
,
鹰鸽博弈:
,
,
囚徒困境只有一个进化稳定策略
,即小团体和对手都选择策略2,小团体对应的收益为3。采用粒子群算法模拟单个种群的进化过程。在该算法中,
,
,
,
,
,
,
,
,
,
,并在前75次迭代中应用变量。
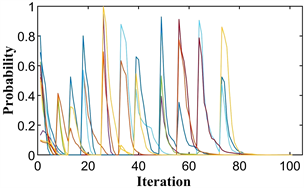
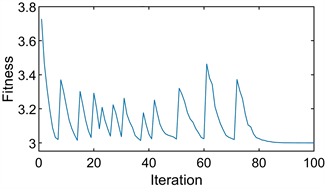
后续仿真实验参数相同。图1(a)显示了进化过程每次迭代的粒子位置。10条曲线代表10个粒子的初始生成,每条曲线代表一个粒子的位置变化。初始位置为
,出现的峰值表明发生了突变,对应于种群中群体策略的突然扰动。在现实中,群体在达到暂时的稳定后,期望获得更多的收益,从而试图改变他们的策略,只是在反复尝试后不稳定,在再次进化后达到稳定点。最终,所有的群体都将停留在那个稳定的点上,不再试图改变他们的策略。图1(b)为最优适应度值在整个进化过程中的变化图像。图1(a)和图1(b)分别对应两次计算的结果。
如图所示,所有粒子都收敛于
,即小群体都选择第二种策略,最佳适应度值为
。这与上面的进化稳定策略几乎相同。由此可见,PPSO清晰地模拟了囚徒困境博弈的整个演化过程,并准确地找到了其进化稳定点。
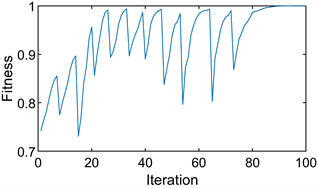
协调博弈有(1, 0)和(0, 1)两个进化稳定的策略,即第一个稳定点表示小团体和对手都选择策略1,第二个稳定点表示小团体和对手都选择策略2。它们是两个纯策略稳定点,前者对应增益2,后者对应增益1。PPSO再次用于模拟单个种群的进化过程。经过多次模拟,得到了两组代表不同结果的图形。
 (a) (b)
(a) (b)
Figure 1. The diagram of prisoner’s dilemma game. (a) Particle location diagram; (b) Optimal fitness diagram
图1. 囚徒困境博弈示意图。(a) 粒子位置图;(b) 最优适应度图
 (a) (b)
(a) (b)
Figure 2. The diagram of the coordination game with evolutionary result
. (a) Particle location diagram; (b) Optimal fitness diagram
图2. 演化结果为
的协调博弈图。(a) 粒子位置图;(b) 最优适应度图

 (a) (b)
(a) (b)
Figure 3. The diagram of the coordination game with evolutionary result
. (a) Particle location diagram; (b) Optimal fitness diagram
图3. 演化结果为
的协调博弈图。(a) 粒子位置图;(b) 最优适应度图
第一个结果对应图2(a)和图2(b),第二个结果对应图3(a)和图3(b)。这两个结果的出现是因为博弈模型有两个稳定点。图2(a)和图3(a)表示进化过程每次迭代的粒子位置图,图2(b)和图3(b)表示最佳适应度变化图。
从图中可以明显看出,图2(a)和图2(b)中的所有粒子都以
的最佳适应度值收敛到
,而图3(a)和图3(b)中的所有粒子都以
的最佳适应度值收敛到
。由此可见,PPSO不仅可以模拟单个纯策略稳定点的种群进化过程,而且可以清晰地处理两个稳定点。同时,精确地导出了两个进化稳定点对应的粒子位置和自适应。
经过300次模拟,发现进入第一个进化稳定点的概率约为
,进入第二个进化稳定点的概率约为
。
我们的分析表明,进化结果很容易落入第一个稳定点,因为第一个稳定点的收益高于第二个稳定点的收益。同时,在此计算中,随着10个粒子的放置,落在第一个稳定点的概率显著增加。
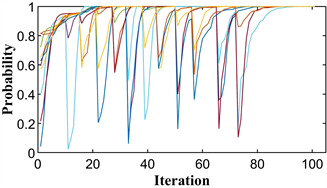
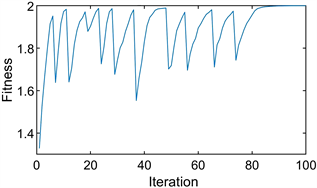
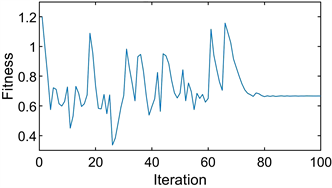
单种群鹰鸽博弈的混合策略进化稳定点为
,即种群中有
个小群体选择策略1,其余小群体选择策略2,小群体对应的收益为
。图4(a)显示了进化过程中每次迭代的粒子位置,图4(b)显示了最佳适应度变化。

 (a) (b)
(a) (b)
Figure 4. The diagram of the hawk-dove game. (a) Particle location diagram; (b) Optimal fitness diagram
图4. 鹰鸽博弈示意图。(a) 粒子位置图;(b) 最优适应度图
由图可知,所有粒子都收敛到
,最佳适应度值为
。由此可见,PPSO不仅可以模拟纯进化稳定策略下的单个种群的进化过程,而且可以清晰地模拟混合策略下的种群。并精确地导出了该稳定点对应的粒子位置和适应度。
6. 参数分析
基于以上的原理分析和对进化路径的模拟,变异在进化过程中起着重要的作用。为了深入探讨变异对进化结果的影响,本节将分析变异程度对进化结果的影响。
PPSO计算过程显示,整个博弈在前75次执行突变操作,选择粒子总数中的
进行突变。这里我
们考虑降低变异度对进化结果的影响。以囚徒困境博弈为例,我们设置10个粒子,迭代次数为30次,在前10次迭代中进行变异。其余参数保持不变,后续仿真实验参数相同。得到的进化路径图如图5(a)和图5(b)所示。
这两幅图共同观察到,在两个实验中只有一个变异的情况下,但进化的结果却完全不同。图5(a)显示了整个博弈最终稳定在一个非进化稳定点。图5(b)显示了博弈在一个进化稳定点稳定下来。为什么在相同的前提条件下会出现不同的结果?通过分析得到,变异的存在并不能决定进化稳定点的成功实现。更深层次的原因是突变粒子的位置。

 (a) (b)
(a) (b)
Figure 5. Particle position diagram of the prisoner’s dilemma game under weak variation. (a) Not evolved to evolutionary stability point; (b) Evolved to evolutionary stability point
图5. 弱变异下囚徒困境博弈的粒子位置图。(a) 没有进化到进化稳定点;(b) 进化到进化稳定点
具体来说,我们将粒子位置分为两部分。第一部分是初始粒子所在的范围,即初始粒子所包围的面积。初始粒子中从粒子顶部位置到粒子底部位置的范围如图5(a)所示。第二部分是初始粒子不存在的范围,即从初始粒子中最低粒子的位置到图5(a)中
的范围。迭代后的第一部分和第二部分也是这样定义的。如果进化稳定点在第二部分,仅受模仿和行为惯性影响的迭代只能保证粒子将第一部分的范围扩展一小部分。膨胀的部分仍然不包含进化稳定点。如图5(a)所示,第一部分经过四次迭代后的范围。粒子迭代到收敛,然后一部分粒子发生突变。如果突变粒子停留在第一部分的范围内,那么整个博弈就不会稳定在进化稳定点,如图5(a)所示。如果突变粒子进入第二部分的范围,则第一部分将被扩展,第一部分将非常接近进化稳定点。例如,在图5(b)的第10次迭代时,橙色粒子在第二部分突变到接近
的位置。在这种情况下,整个游戏可以稳定在进化稳定点。
为什么当第一部分非常接近或包含进化稳定点时,整个博弈模型在进化稳定点稳定?从图中可以看出,粒子越接近进化稳定点,其收益越高,其他粒子越容易模仿和学习。因此其他粒子向它靠近。最终,所有的粒子都稳定在进化稳定点。
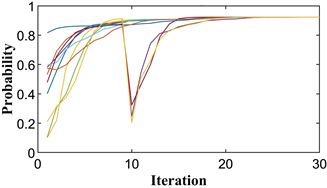
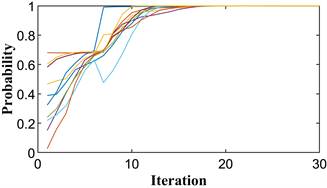 (a) (b)
(a) (b)
Figure 6. Particle position diagram of the coordination game under weak variation. (a) Not evolved to evolutionary stability point; (b) Evolved to evolutionary stability point
图6. 弱变异下协调博弈的粒子位置图。(a) 没有进化到进化稳定点;(b) 进化到进化稳定点
通过以上分析可以得出,只有当第一部分的位置非常接近或包含进化稳定点时,整个博弈才能稳定在进化稳定点。当正常迭代后的第一部分不是很接近或包含进化稳定点时,要求突变粒子的突变位置使第一部分非常接近或包含进化稳定点,则整个博弈在进化稳定点是稳定的。反之它将稳定到非进化稳定点。
下面,我们通过协调博弈和鹰鸽博弈的仿真实验来验证这一结论。
图6(a)和图6(b)显示了两个模拟中只有一个变异的协调博弈的进化路径。第一个图显示了整个博弈稳定在两个图一起观察的非进化稳定点。第二个图表明整个博弈在进化稳定点稳定。在图6(a),变异粒子保持在范围的第一部分。在图6(b)中,变异粒子在第二部分进入
的位置。突变粒子保持在第一部分范围内的模拟稳定在非进化稳定点。突变粒子突变到第二部分范围的模拟在进化稳定点稳定。这一结果与上述囚徒困境博弈模拟结果一致。协调博弈的仿真验证了我们的分析。
 (a) (b)
(a) (b)
Figure 7. Particle position diagram of the hawk-dove game under weak variation. (a) Variant operation exists; (b) No variant operation
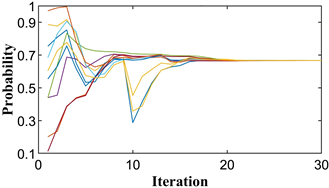
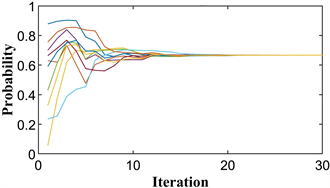
图7. 弱变异条件下鹰鸽博弈的粒子位置图。(a) 存在变异结果;(b) 无变异结果
图7(a)和图7(b)显示了两种模拟下鹰鸽博弈的进化路径。从这两幅图来看,第一幅和第二幅图都表明整个游戏在进化稳定点稳定下来。根据结论,粒子越接近进化稳定点,就越容易模仿和学习其他粒子。所有的粒子都向它靠近,并最终稳定在进化稳定点。在鹰鸽博弈模拟中,初始粒子范围的第一部分直接包含了进化稳定点,因此变异操作并不影响进化稳定点的成功实现。可以看出,所有的粒子都在向进化稳定点靠近,并最终稳定在进化稳定点上。这种现象与结论的内容是一致的。鹰鸽博弈的仿真结果同样验证了我们的分析。
7. 结论
怎么实现种群的进化过程是一个重要的问题。大多数人用博弈论的框架来研究这个问题,得到种群是如何进化到稳定状态的。本文通过对粒子群算法进行改进,进而来研究种群的进化过程。粒子群优化算法的原理是基于对动物群体活动的观察,以及群体中的个体如何利用信息共存来推动整个群体在问题解决空间中的移动。粒子群算法通过速度和位置的迭代公式来找到函数的极值点,用极值点来优化问题。本文利用进化博弈中个体模仿成功行为的特性对粒子群算法进行了改进,即种群粒子群优化算法,从而来解决种群进化问题。
该算法在博弈论框架下成功地模拟了具有收益矩阵的单种群的进化过程,并且用模仿和学习成功的过程来描述行为的扩散。在粒子群算法中,小群体可以看作是一个粒子,群体中所有个体策略的变化都类似于粒子对最优解的搜索。为了寻找更好的收益,还充分考虑了种群有实际的扰动情况。
对三个经典的博弈模型(囚徒困境,协调博弈,鹰鸽博弈)进行仿真实验,来评估PPSO算法的准确性。囚徒困境只有一个进化稳定策略,协调博弈有两个进化稳定策略,鹰鸽博弈有一个混合策略进化稳定策略。PPSO在迭代过程中都清晰地显示了每个粒子的位置,并找到了稳定点的进化路径。所以无论是单点纯策略,单点混合策略,还是多点纯策略,并且模拟结果与理论结果的进化稳定策略几乎一样。本文进一步探讨了变异对进化结果的影响。根据参数分析,发现稳定进化点的实现不仅与突变有关,而且与突变的程度有重要关系。如果初始粒子的范围不包含进化稳定点,则只有当粒子突变到进化稳定策略的选定范围时,整个博弈模型才能最终稳定在进化稳定点。
本文通过改进粒子群算法来研究种群的进化过程,粒子群算法可以适用于研究更新机制是如何促进合作的发展,如模仿过程,Moran过程,愿望驱动。这将是我们接下来更值得研究的问题。
基金项目
国家自然科学基金项目(71961003);贵州省科技厅联合基金项目(黔科合LH字[2017]7223);贵州大学博士基金(贵大人基合字[2019]49)。
致谢
我们衷心感谢匿名编辑和审稿人的热情工作。
NOTES
*通讯作者。