一种分数阶急性虫媒传染病模型的参数识别方法研究

Parameter Identification for a Fractional Dynamical Epidemic Model of Dengue Fever

摘要: 针对分数阶急性虫媒传染病模型系统参数识别问题，基于Gorenflo-Mainardi-Moretti-Paradisi (GMMP)格式和牛顿法，提出了一种求解分数阶急性虫媒传染病模型系统的数值方法。将改进的混合Nelder-Mead单纯形搜索和粒子群算法(PSO)运用到分数阶微分方程的分数阶和系数识别。仿真实验表明，获得的分数阶急性虫媒传染病模型系统比其他模型能提供更符合实际数据的数值结果。

Abstract: In order to solve the problem of parameter identification for a fractional dynamical epidemic model of dengue fever, a numerical technology is proposed based on the Gorenflo-Mainardi-Moretti- Para-disi (GMMP) formula and the Newton method in this paper. The improved algorithm (MH- NMSS-PSO) combining Nelder Mead simplex search and particle swarm optimization is applied to the fractional order and coefficient identification of the fractional differential equations. Simulation experiments show that the obtained fractional dengue fever model can provide better numerical results that agree very well with the real data.

1. 引言

根据世界卫生组织(WHO)的报告，在过去的几十年里，全球每年有近4亿急性虫媒传染病感染病例，其中大多数是儿童，危害严重 [1] 。近年来，众多国内外学者对急性虫媒传染病病毒在宿主和媒介之间传播的数学模型进行了深入细致地研究，得到了一些重要成果。Nishiura研究了急性虫媒传染病传播的数学模型和统计分析 [2] 。Helena et al.研究了经典急性虫媒传染病模型的稳定性 [3] 。Sardar提出了一个具有记忆的急性虫媒传染病传播数学模型 [4] 。分数阶导数比整数阶导数更适合描述与非定域性相关的现象，因为分数阶导数为描述带有记忆和遗传特性的过程提供了一个极好的工具 [5] [6] 。所以，基于流行病系统的分数阶导数也被用于处理一些流行病行为 [7] 的建模。分数阶导数具有与整数阶导数的局部算子相反的非局部运算，而且，当分数阶系统适用于实际数据时，它比整数阶系统多了一个自由度。于是，Pooseh等人 [8] 研究了具有同阶Riemann-Liouville型导数的分数阶急性虫媒传染病模型系统。Diethelm [9] 提出了一种基于Caputo型导数的分数阶模型来模拟急性虫媒传染病暴发，其中一些阶数是相同的。然而，在这些研究论文中，急性虫媒传染病模型的参数是直接给出的，或者模型系统的数值解与实际数据匹配比较差。因此，本文运用Caputo导数提出一个新的通用的分数阶急性虫媒传染病模型系统，为了得到该分数阶急性虫媒传染病模型系统的数值解，修改了Gorenflo-Mainardi-Moretti-Paradisi (GMMP)格式 [10] [11] ，基于Grünwald-Letnikov公式 [6] 和分数阶导数的性质，GMMP格式可以作为隐式差分格式得到，这种隐式差分格式可以看作是一个非线性方程组。在求解非线性方程组时，采用牛顿法求解隐式差分格式。在获得模型数值解的基础上，利用改进的GAM算法及融合Nelder-Mead单纯形搜索和粒子群优化(PSO)的算法(MH-NMSS-PSO)识别模型系统新的分数阶和参数。仿真实验表明获得的分数阶急性虫媒传染病模型系统能够提供比其他模型更符合实际数据的数值结果。

2. 分数阶急性虫媒传染病模型系统

急性虫媒传染病流行病的经典模型 [2] 通常将整个人群 $N_h$ 被分为三类人群：易感人群 $S_h\left(t\right)$ ，感染者 $I_h\left(t\right)$ ，具免疫的感染者(移出者) $R_h\left(t\right)$ 。雌蚊总数 $N_m$ 分为两组：雌蚊敏感 $S_m\left(t\right)$ 和被感染的雌性蚊子 $I_m\left(t\right)$ 。急性虫媒传染病经典模型由五个常微分方程组成，形式如下：

$\{\begin{array}{l}\frac{\text{d}{S}_h}{\text{d}t}={\mu }_h\left(N_h-S_h\right)-\frac{{\beta }_{h}b}{N_h+m}{S}_h{I}_m\hfill \\ \frac{\text{d}{I}_h}{\text{d}t}=\frac{{\beta }_{h}b}{N_h+m}{S}_h{I}_m-\left({\mu }_h+\gamma \right)I_h\hfill \\ \frac{\text{d}{R}_h}{\text{d}t}=\gamma I_h-{\mu }_h{R}_h\hfill \\ \frac{\text{d}{S}_m}{\text{d}t}={\mu }_m\left(N_m-S_m\right)-\frac{{\beta }_{m}b}{N_h}{S}_m{I}_h\hfill \\ \frac{\text{d}{I}_m}{\text{d}t}=\frac{{\beta }_{m}b}{N_h+m}{S}_m{I}_h-{\mu }_m{I}_m\hfill \end{array}$ (1)

在此(1)系统中的参数分别表示不同的含义：

(i) ${\mu }_h$ 是人均死亡率(即平均寿命的倒数)；

(ii) $\gamma$ 是人类的康复率，也就是从被感染到有免疫力的平均时间的倒数；

(iv) b是叮咬率，即每天每只蚊子平均叮咬的次数；

(v) ${\beta }_h$ 和 ${\beta }_m$ 分别表示人与蚊子之间的传播概率，反之亦然；

(vi) m表示可供蚊子选择的(非人类)血液来源的数量。

在文献 [3] 中参数已确定如下数值：

${\mu }_h=\frac{1}{71.365},{\mu }_m=\frac{1}{10},{\beta }_h={\beta }_m=0.36,b=0.7,\gamma =\frac{1}{3},m=0$ . (2)

初始条件如下：

$S_h\left(0\right)=55784,I_h\left(0\right)=216,R_h\left(0\right)=0,S_m\left(0\right)=168000,I_m\left(0\right)=0$ . (3)

这些初始条件表明，这个偏远岛屿(佛得角群岛)上的蚊子种群最初是健康的，病毒是通过被感染的人旅行传入生态系统的。此外，据了解，人类是佛得角群岛蚊子的唯一血液来源，所以在本文中设定 $m=0$ 。利用Matlab中的ODE45函数可以得到微分方程系统(1)的数值解。结果如图1所示，表明该微分方程系统的解与感染人数的实际匹配较差。

Figure 1. Comparison between numerical results of classical model (1) and actual data

图1. 经典模型(1)的数值结果与实际数据比较

近年来，已有不少分数阶传染病模型系统来分析模拟传染病传播行为。与基于整数阶导数的经典模型相比，分数阶模型系统可以在测量数据和模拟数据之间提供更好的一致性 [7] 。由此启发下，提出一个新的通用的分数阶急性虫媒传染病模型系统，使用了不同阶的Caputo导数：

$\{\begin{array}{l}{\lambda }_{\alpha 1}{}_0{}^{C}D{}_t^{\alpha 1}{S}_h={\mu }_h\left(N_h-S_h\right)-\frac{{\beta }_{h}b}{N_h+m}{S}_h{I}_m\hfill \\ {\lambda }_{\alpha 2}{}_0{}^{C}D{}_t^{\alpha 2}{I}_h=\frac{{\beta }_{h}b}{N_h+m}{S}_h{I}_m-\left({\mu }_h+\gamma \right)I_h\hfill \\ {\lambda }_{\alpha 3}{}_0{}^{C}D{}_t^{\alpha 3}{R}_h=\gamma I_h-{\mu }_h{R}_h\hfill \\ {\lambda }_{\alpha 4}{}_0{}^{C}D{}_t^{\alpha 4}{S}_m={\mu }_m\left(N_m-S_m\right)-\frac{{\beta }_{m}b}{N_h}{S}_m{I}_h\hfill \\ {\lambda }_{\alpha 5}{}_0{}^{C}D{}_t^{\alpha 5}{I}_m=\frac{{\beta }_{m}b}{N_h+m}{S}_m{I}_h-{\mu }_m{I}_m\hfill \end{array}$ (4)

其中， ${}_0{}^{C}D{}_t^{\alpha i}$ 为第 ${\alpha }_i$ 阶的Caputo分数阶导数；参数 ${\mu }_h$ 、 ${\beta }_h$ 、b、 $\gamma$ 和 ${\mu }_m$ 如式(1)所示。Pooseh et al. [8] 研究了具有相同阶数的Riemann-Liouville型导数的分数阶急性虫媒传染病模型系统，其中Riemann-Liouville微分方程无法与经典初始条件结合。Diethelm [9] 提出了带有Caputo型导数的分数阶模型来模拟急性虫媒传染病的爆发，其中 ${\alpha }_h={\alpha }_1={\alpha }_2={\alpha }_3$ 且 ${\alpha }_m={\alpha }_4={\alpha }_5$ 。参照文献 [9] 选取 ${\alpha }_h=1$ 和 ${\alpha }_m=0.77$ 的参数，仿真结果如图2所示，表明分数阶模型系统比整数阶模型系统具有更好的匹配性(1)。均方相对误差为 $g=0.988$ ，说明匹配的效果可以进一步提高。

Figure 2. Comparison between numerical results and actual data of fractional order model system [9]

图2. 分数阶模型系统 [9] 的数值结果与实际数据的比较

3. 分数阶微分方程的数值求解方法

目前已有多种数值方法来求解分数阶模型系统(4)，包括幂级数法 [5] 、Millin变换法 [5] 和预估–校正方法 [6] 及其他方法 [9] 。本文采用GMMP格式 [12] 和牛顿法求解(4)式，比其他方法效率更高。

为简单起见，模型系统(4)可改写为 $\lambda {}_a{}^{C}D{}_t^{\alpha }x\left(t\right)=f\left(t,x\left(t\right)\right)$ ，其中 $x\left(t\right)={\left(S_h,I_h,R_h,S_m,I_m\right)}^{\text{T}}$ 。假设在一统一网格上进行 $t_j=a+jh,j=0,1,2,\cdots ,N,Nh=t-a$ ，且 $a>0$ 。那么可以使用以下公式近似计算Riemann-Liouville和Grünwald-Letnikov分数阶导数，

${}_a{}^{RL}D{}_t^{\alpha }x\left(t\right)={}_a{}^{GL}D{}_t^{\alpha }x\left(t\right)=\underset{h\to 0}{\lim }\frac{1}{h^{\alpha }}{\displaystyle \underset{k=0}{\overset{N}{\sum }}{c}_k^{\alpha }}x\left(t_{N-k}\right)\approx \frac{1}{h^{\alpha }}{\displaystyle \underset{k=0}{\overset{N}{\sum }}{c}_k^{\alpha }}x\left(t_{N-k}\right)$ (5)

而Caputo分数阶导数可用下列关系近似表示

${}_a{}^{C}D{}_t^{\alpha }x\left(t\right)\approx \frac{1}{h^{\alpha }}{\displaystyle \underset{k=0}{\overset{N}{\sum }}{c}_k^{\alpha }}\left(x\left(t_{N-k}\right)-{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\frac{{\left(t-a\right)}^j{x}^{\left(j\right)}\left(a\right)}{j!}}\right)$ (6)

其中 $c_k^{\alpha }={\left(-1\right)}^k\left(\begin{array}{c}\alpha \\ j\end{array}\right)$ 是二项式系数。

该方案模式首先在文献 [12] 中引入且在文献 [10] 中称为GMMP方案模式。基于该GMMP格式(6)，提出了数值模拟分数阶微分方程的方法。为说明该方法，考虑分数阶非线性方程(4)如下

$\begin{array}{l}\lambda {}_a{}^{C}D{}_t^{\alpha }x\left(t\right)=f\left(t,x\left(t\right)\right),0\le t\le T\\ x^{\left(k\right)}\left(a\right)=x_0^{\left(k\right)},k=0,1,\cdots ,n-1\end{array}$ (7)

其中 ${}_a{}^{C}D{}_t^{\alpha }$ 表示Caputo定义的分数阶导数。

由式(6)有

$\lambda {\displaystyle \underset{k=0}{\overset{N}{\sum }}{c}_k^{\alpha }}\left(x\left(t_N{}_{-k}\right)-{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\frac{{\left(t-a\right)}^j{x}^{\left(j\right)}\left(a\right)}{j!}}\right)=h^{\alpha }f\left(t_N,x\left(t_N\right)\right)$ , (8)

即

$x\left(t_N\right)=h^{\alpha }/\lambda f\left(t_N,x\left(t_N\right)\right)+{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\frac{{\left(t-a\right)}^j{x}^{\left(j\right)}\left(a\right)}{j!}}-{\displaystyle \underset{k=1}{\overset{N}{\sum }}{c}_k^{\alpha }}\left(x\left(t_N{}_{-k}\right)-{\displaystyle \underset{j=0}{\overset{n-1}{\sum }}\frac{{\left(t-a\right)}^j{x}^{\left(j\right)}\left(a\right)}{j!}}\right)$ . (9)

特别地，若令 $0<\alpha \le 1$ ，则式(9)可简化为

$x\left(t_N\right)=h^{\alpha }/\lambda f\left(t_N,x\left(t_N\right)\right)+x\left(a\right)-{\displaystyle \underset{k=1}{\overset{N}{\sum }}{c}_k^{\alpha }}\left(x\left(t_N{}_{-k}\right)-x\left(a\right)\right)$ . (10)

基于Grünwald-Letnikov公式，提出了一种隐式差分格式(10)。可以把式(10)看成是关于未知变量 $x\left(t_N\right)$ 的方程，该变量位于非线性方程的两侧。那么就可以使用牛顿法通过方程(10)求解 $x\left(t_N\right)$ 的值。牛顿法是求解非线性方程组的一种有效方法，对于非线性方程 $f\left(x\right)=0$ ，牛顿法的公式如下：

$x_{n+1}=x_n-J_F{\left(x_n\right)}^{-1}F\left(x_n\right),n=0,1,2,\cdots$ (11)

其中 $J_F\left(x_n\right)$ 为Jacobian矩阵。为了描述牛顿算法的确定性，这里使用 $J_F\left(x_n\right)$ 的LU因式分解。

4. 分数阶非线性动力系统参数识别

参数识别是很困难的，当参数的范围是未知的并且函数f对于未知参数来说是高度非线性的时候，尤其如此。本节提出一种识别分数阶非线性动力系统参数的方法。该方法确定的分数阶动力系统可以写成具有m个未知参数的系统：

$\begin{array}{l}{}_a{}^{C}D{}_t^{\alpha }x\left(t\right)=f\left(t,x\left(t\right),p_1,p_2,\cdots ,p_m\right),0\le t\le T,\\ x^{\left(k\right)}\left(a\right)=x_0^{\left(k\right)},k=0,1,\cdots ,n-1\end{array}$ (12)

其中 $x={\left(x_1,x_2,\cdots ,x_n\right)}^{\text{T}}$ ， $f={\left(f_1,f_2,\cdots ,f_n\right)}^{\text{T}}$ 是n维函数向量，而 $f_i\left(i=1,2,\cdots ,n\right)$ 对于未知参数 $p_i\left(i=1,2,\cdots ,m\right)$ 有可能是非线性的，m是参数的个数。基于刘发旺教授提出的非线性动力系统中识别参数的网格逼近法(GAM) [11] 。对网格逼近法进行了改进(称为MGAM)，使其能够动态逐步识别参数。

新的算法(MH-HMSS-PSO)是融合Nelder-Mead单纯形搜索方法(NMSS) [13] 和粒子群优化(PSO)算法 [14] 来优化多峰函数的。NMSS侧重于“开发”，PSO侧重于“探索”。NMSS和PSO之间存在一些差异：首先，初始点的选取不一样，初始点在NMSS中是预先确定的，但在粒子群算法中是一组随机点。其次，算法向前迭代的方向和条件也不一样，NMSS的演化是从函数值最差的点开始的，而粒子群算法则是从性能较好的点开始的 [15] 。

设 $\left(p_1,p_2,\cdots ,p_m\right)\in D$ ，其中D是一参数空间的有界域

$D=\left[p_1^{\left(\min \right)},p_1^{\left(\max \right)}\right]\times \left[p_2^{\left(\min \right)},p_2^{\left(\max \right)}\right]\times \cdots \times \left[p_m^{\left(\min \right)},p_m^{\left(\max \right)}\right]$ . (13)

通过优化如下均方根相对误差函数确定近似估计未知参数 $\left(p_1^{\ast },p_2^{\ast },\cdots ,p_m^{\ast }\right)$ 。

$g\left(P^{*}\right)=\underset{P\in D}{\lim }g\left(P\right)=\underset{P\in D}{\lim }\left\{\sqrt{\frac{{\displaystyle {\sum }_{j=0}^N{\left(\left(x\left(t_j\right)-x_j\right)/x_j\right)}^2}}{N+1}}\right\}$ (14)

其中 $x\left(t_j\right)$ 是在给定参数 $P=\left(p_1,p_2,\cdots ,p_m\right)$ 下分数阶系统(4)的数值解，而 $x_j$ 是实际值。具体的算法步骤如下。

步骤1：初始化。产生 $3m+1$ 规模的种群。为最小化m个变量(未知参数)的函数 $g\left(P\right)$ ，产生 $m+1$ 个向量点 $P_i=\left(p_{1,i},p_{2,i},\cdots ,p_{m,i}\right)\in D,\left(i=1,2,\cdots ,m+1\right)$ 形成m维度的单纯形，即

$P_i=\left(p_{1,i},p_{2,i},\cdots ,p_{m,i}\right)\in D,i=1,2,\cdots ,m+1$ (15)

其中

$p_{j,i}=p_j^{\left(\min \right)}+\left(i-1\right)\times \left(p_j^{\left(\max \right)}-p_j^{\left(\min \right)}\right)/\left(m+1\right),j=1,2,\cdots ,m;i=1,2,\cdots ,m+1$ . (16)

在PSO算法部分中，两个粒子随机产生向量点

$P_i=\left(p_{1,i},p_{2,i},\cdots ,p_{m,i}\right)\in D,i=m+2,\cdots ,3m+1$ (17)

其中

$p_{j,i}=p_j^{\left(\min \right)}+Rand\times \left(p_j^{\left(\max \right)}-p_j^{\left(\min \right)}\right),j=1,2,\cdots ,m;i=m+2,\cdots ,3m+1$ , (18)

Rand是(0, 1)中的随机数，粒子在每个维度的初始向量依据下式选择

$V_{j,i}=\left(V_j^{\left(\max \right)}-V_j^{\left(\min \right)}\right)/L_j,j=1,2,\cdots ,m;i=m+2,\cdots ,3m+1$ (19)

其中 $L_j$ 是选取好的整数。

步骤2：评估和排序：评估每个粒子的目标函数值 $g\left(P\right)$ ，根据函数值大小进行排序， $g\left(P_1\right)\le g\left(P_2\right)\le \cdots \le g\left(P_{3m+1}\right)$ 。

步骤3：NMSS算法：运用NMSS算子从 $m+1$ 粒子中找到最佳，并替换第 $m+1$ 个粒子：计算除 $P_{m+1}$ 外所有点的重心 $P_o=\left(p_{1,o},p_{2,o},\cdots ,p_{m,o}\right)\in D$ ，其中 $P_{j,o}={\displaystyle {\sum }_{i=1}^m{p}_{j,i}/m},j=1,2,\cdots ,m$ 。映像点为 $P_r=\left(1+\alpha \right)P_o-\alpha P_{m+1}$ 。

其中 $\alpha$ 是映像参数( $\alpha >0$ )。Nelder和Mead建议取 $\alpha =1$ [13] ，那么分别有三种情形：

情形1： $g\left(P_1\right)\le g\left(P_r\right)\le g\left(P_m\right)$ ，则 $P_r$ 替换 $P_{m+1}$ ；

情形2： $g\left(P_r\right)\le g\left(P_1\right)$ ，则计算扩展点 $P_e=\gamma P_r+\left(1+\gamma \right)P_o$ ；若 $g\left(P_r\right)\le g\left(P_1\right)$ ， $P_e$ 替换 $P_{m+1}$ ，否则 $P_r$ 替换 $P_{m+1}$ 。Nelder和Mead建议取 $\gamma =2$ [13] ；

情形3： $g\left(P_r\right)\ge g\left(P_m\right)$ ，若 $g\left(P_r\right)\le g\left(P_{m+1}\right)$ ， $P_r$ 替换 $P_{m+1}$ 。计算收缩点 $P_c=\beta P_{m+1}+\left(1-\beta \right)P_c$ ；若 $g\left(P_c\right)\le g\left(P_{m+1}\right)$ ， $P_r$ 替换 $P_{m+1}$ ，否则令 $P_i=\sigma P_i+\left(1-\sigma \right)P_1,i=1,2,\cdots ,m+1$ 。Nelder和Mead建议取 $\beta =\sigma =0.5$ [13] 。

步骤4：粒子群优化：应用PSO算子 [15] 对目标函数值最差的2m个粒子进行更新。

步骤5：若停止准则 $S_c<\epsilon$ 满足，则停止迭代，否则转步骤2。这里的停止准则定义如下：

$S_c={\left[{\displaystyle \underset{i=1}{\overset{m+1}{\sum }}\frac{{\left(\bar{g}-\sqrt{g_i}\right)}^2}{m+1}}\right]}^{\frac{1}{2}}$ (20)

其中 $\bar{g}={\displaystyle {\sum }_i^{m+1}\frac{g_i^{*}}{m+1}}$ ， $g_i^{*}=\sqrt{g_i}=\sqrt{g_i\left(p_1,p_2,\cdots ,p_m\right)}$ 。

5. 在分数阶急性虫媒传染病模型系统参数识别中的应用

为了识别分数阶急性虫媒传染病系统的参数，使用Diethelm [9] 给出的佛得角急性虫媒传染病暴发的实际数据作为已知数据来进行参数识别。有五个分数阶和六个需要识别的参数。在求解过程中，取未知参数向量为 $P=\left({\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4,{\alpha }_5,{\mu }_h,{\beta }_h,b,\gamma ,{\mu }_m,{\beta }_m\right)$ 。

使用MH-NMSS-PSO来识别分数阶急性虫媒传染病系统的参数。对于MH-NMSS-PSO方法来说，选择合适的区间是非常重要的，如果区间较窄，则采用MH-NMSS-PSO方法可以快速确定结果，因此首先使用MGAM来选择最佳的区间隔。基于这些区间，使用MH-NMSS-PSO算法来识别分数阶和参数，再根据上述MGAM的结果，选择一些合适的区间和初速度，如下所示：

$\begin{array}{l}0.8\le {\alpha }_1=p_1\le 1,0.8\le {\alpha }_2=p_2\le 1,0.8\le {\alpha }_3=p_3\le 1,\\ 0.7\le {\alpha }_4=p_4\le 1,0.7\le {\alpha }_5=p_5\le 1,3\times {10}^{-5}\le {\mu }_h=p_6\le 7\times {10}^{-5},\\ 0.1\le {\beta }_h=p_7\le 0.5,0.4\le b=p_8\le 0.8,0.2\le \gamma =p_9\le 0.6,\\ 0.001\le {\mu }_m=p_{10}\le 0.2,0.2\le {\beta }_m=p_{11}\le 0.6\end{array}$

而 $V_1=V_2=V_3=V_4=V_5=0.01$ ， $V_6=1\times {10}^{-6}$ ， $V_7=V_8=V_9=V_{10}=V_{11}=0.01$ 。

利用目标函数 $g\left(P\right)$ 潜在的全局最小值，可以进一步得到未知参数 $P^{*}$ 如下所示

$\begin{array}{l}{\alpha }_1=p_1=0.9997,{\alpha }_2=p_2=0.9989,{\alpha }_3=p_3=0.9672,\\ {\alpha }_4=p_4=0.9018,{\alpha }_5=p_5=0.9891,{\mu }_h=p_6=5.1546\times {10}^{-5},\\ {\beta }_h=p_7=0.4942,b=p_8=0.6094,\gamma =p_9=0.4526,\\ {\mu }_m=p_{10}0.0100,{\beta }_m=p_{11}=0.2154\end{array}$

此时的均方根相对误差 $g\left(P^{*}\right)=0.\text{41}5$ 。

图3显示MH-NMSS-PSO法识别参数获得的分数阶模型系统参数 $P^{*}$ 的数值解与实际数据具良好的一致性，该算法的均方根相对误差 $g=0.415$ 小于MGAM算法(图4所示)。在其他参数固定的情况下，还研究了所有参数对感染人数 $I_h\left(t\right)$ 的影响，结果与MGAM算法一致。说明MH-NMSS-PSO在处理分数阶急性虫媒传染病系统的反问题时也是有效的。然而，由于MHNMSS-PSO算法对参数区间内初始点的选择非常敏感，且不能保证达到全局最优，因此在使用MHNMSS-PSO算法时必须小心。

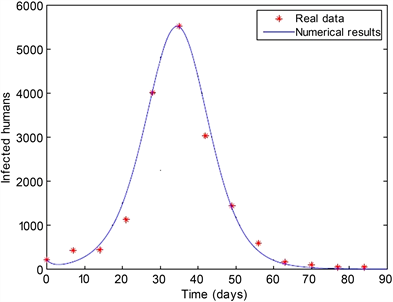
Figure 3. Comparison of numerical results with the estimated parameters obtained by MH-NMSS-PSO with real data

图3. 分数阶系统(MH-NMSS-PSO)的数值结果与实际数据的比较

Figure 4. Comparison of numerical results with the estimated parameters obtained by MGAM with real data

图4. 分数阶系统(MGAM)的数值结果与实际数据的比较

6. 结论

本文提出了一种基于Caputo分数阶导数的急性虫媒传染病模型系统。研究了分数阶急性虫媒传染病模型系统参数识别的逆问题。采用改进的混合Nelder-Mead单纯形搜索和粒子群优化算法对分数阶微分方程进行参数识别。改进的算法比经典算法效率更高，而且获得的分数阶急性虫媒传染病系统能够提供与真实数据更为匹配的数值结果。实验结果还表明，本文提出的模型参数识别方法也可以应用于其他分数阶流行病毒传播模型的刻画。

基金项目

福建省自然科学基金(项目编号：2021J011031)，闽江学院校长基金(项目编号：103952023045)。