单纯形上多元Lagrange插值问题研究

Research on Multivariate Lagrange Interpolation on Simplexes

摘要: 以四面体框架上的Lagrange插值研究为基础，进一步研究了高维空间中单纯形上的Lagrange插值。给出了构造超四面体框架上四元Lagrange插值可解结点组的迭代方法，并给出了n维空间中单纯形上的Lagrange插值算法，最后给出具体实例进行验证。

Abstract: Building upon the research on Lagrange interpolation in the framework of tetrahedra, this study further investigates Lagrange interpolation on simplices in high-dimensional spaces. An iterative method is proposed for constructing solvable node sets for four-element Lagrange interpolation on hyper-tetrahedra frameworks. Additionally, a Lagrange interpolation algorithm on simplices in n-dimensional space is provided. Finally, specific examples are presented to validate the proposed approach.

1. 引言

多元Lagrange插值是计算数学领域的一个重要研究课题(由文献 [1] )，在进行关于多元函数插值的研究时，多元插值函数的适定性问题是一个基本问题。国内外有关这一问题的研究主要分为两类，一类是给定插值空间，去构造适定的插值结点组；另一类是给定结点组，去构造具有最低可能次数的正则插值空间。目前，关于在整个空间进行插值以及关于定义于空间中一般代数流形上进行Lagrange插值的研究比较多 [2] ，在有关单纯形上Lagrange插值问题的研究中，以往的学者研究了三角形网格和四面体框架上的Lagrange插值方法(由文献 [1] [3] [4] )，而在四维空间或更高维空间中的单纯形上进行Lagrange插值的研究并不多见。梁学章等人在 [5] 中讨论了高维空间中代数流形上多元Lagrange插值问题，在 [6] 中讨论了C^s中的多元Lagrange插值及插值适定结点组的构造，张洁琳在 [7] 中深入研究了n元函数的Lagrange插值问题。本文主要讲述高维空间中单纯形上的多元Lagrange插值。

单纯形上的多元Lagrange插值在许多科学研究中有广泛的应用。例如：在材料科学领域，在高维空间中的物理过程建模中，比如四维或更高维的空间，Lagrange插值可用于在单纯形上进行有限元分析，这对于研究人员模拟材料的变形、热传导等物理过程非常有用，有助于优化材料的设计和预测其性能；在医学影像重建中使用高维单纯形上的Lagrange插值可以对离散化的医学影像数据进行插值和重建，从而生成更准确和平滑的图像，改善图像质量、提高分辨率并减少噪声，从而帮助医生进行更准确的诊断和治疗决策。因此，高维空间中单纯形上多元Lagrange插值的研究意义重大。

2. 基本定义和定理

本文主要研究高维空间中单纯形上进行多元Lagrange插值的问题。首先，给出n元Lagrange插值问题的相关定义及定理：

设m为任意整数，n为非负整数， $k,k_1,k_2$ 为自然数，定义符号 $e_m^{\left(n\right)}=\left(\begin{array}{c}m+n\\ n\end{array}\right)$ ，再定义符号 $e_m^{\left(n\right)}\left(k\right)=\left(\begin{array}{c}m+n\\ n\end{array}\right)-\left(\begin{array}{c}m+n-k\\ n\end{array}\right)$ ，及符号

$e_m^{\left(n\right)}\left(k_1,k_2\right)=\left(\begin{array}{c}m+n\\ n\end{array}\right)-\left(\begin{array}{c}m-k_1+n\\ n\end{array}\right)-\left(\begin{array}{c}m-k_2+n\\ n\end{array}\right)+\left(\begin{array}{c}m-k_1-k_2+n\\ n\end{array}\right)$

$P_m^{\left(n\right)}$ 代表所有次数不超过m的n元复系数多项式空间，即

$P_m^{\left(n\right)}=\left\{{\displaystyle \underset{0\le \left|\alpha \right|\le m}{\sum }{a}_{\alpha }}{x}_1^{{\alpha }_1}{x}_2^{{\alpha }_2}\cdots x_n^{{\alpha }_n}|{\alpha }_i\in C\right\}$

其中 $\left|\alpha \right|={\alpha }_1+{\alpha }_2+\cdots +{\alpha }_n$ ， ${\alpha }_i$ 为非负整数。

定义1 ( $P_m^{\left(n\right)}$ 上的插值适定结点组的概念)

设 $A={\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}}$ 是n维复数空间 $C^n$ 中 $e_m^{\left(n\right)}$ 个互不相同的点构成的点集，如果对于任意给定的复数组 ${\left\{q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}}$ ，恒存在一个多项式 $f\left(X\right)\in P_m^{\left(n\right)}$ ，使之满足 $f\left(Q^{\left(i\right)}\right)=q_i,i=1,\cdots ,e_m^{\left(n\right)}$ ，则称 $A={\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}}$ 为 $P_m^{\left(n\right)}$ 上的一个插值适定结点组。

定义2 (k次代数超曲面上的插值适定结点组)

设k为自然数， $P\left(X\right)=0$ 为 $C^n$ 中一个k次无重复分量的代数超曲面，设 $A={\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}\left(k\right)}$ 为超曲面 $P\left(X\right)=0$ 上的 $e_m^n\left(k\right)$ 个互不相同的点构成的点集，若存在一个多项式 $f\left(X\right)\in P_m^{\left(n\right)}$ ，使之对任意给定的复数组 ${\left\{q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}\left(k\right)}$ 都满足插值条件 $f\left(Q^{\left(i\right)}\right)=q_i,i=1,\cdots ,e_m^{\left(n\right)}\left(k\right)$ ，则称 $A={\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}\left(k\right)}$ 为沿k次代数超曲面 $P\left(X\right)=0$ 上的m次插值适定结点组。

定义3 (次数分别为 $k_1,k_2$ 的代数超曲面相交于代数流形上的插值适定结点组)

设 $k_1,k_2$ 为自然数， $S=\left(P_1,P_2\right)$ 为 $C^n$ 中两个次数分别为 $k_1,k_2$ 的无重复分量的代数超曲面 $P_1\left(X\right)=0$ ， $P_2\left(X\right)=0$ 充分相交的代数流形，设 $A={\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}\left(k_1,k_2\right)}$ 为S上的 $e_m^n\left(k_1,k_2\right)$ 个互不相同的点构成的点集，若存在一个多项式 $f\left(X\right)\in P_m^{\left(n\right)}$ ，使之对任意给定的复数组 ${\left\{q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}\left(k_1,k_2\right)}$ 都满足插值条件 $f\left(Q^{\left(i\right)}\right)=q_i,i=1,\cdots ,e_m^{\left(n\right)}\left(k_1,k_2\right)$ ，则称 $A={\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}\left(k_1,k_2\right)}$ 为沿代数流形S上的m次插值适定结点组。

定义4 (单纯形的定义)

定义代数簇 $S_n=\left\{\left(x_1,x_2,\cdots ,x_n\right)\in C^n|x_1+x_2+\cdots +x_n\le 1,x_i\ge 0,i=1,2,\cdots ,n\right\}$ 作为几何对象，称 $S_n$ 为单纯形。

定理1 (基本定理)

${\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}}$ 是 $P_m^{\left(n\right)}$ 中的一个m次插值适定结点组当且仅当 ${\left\{Q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}}$ 不落在 $P_m^{\left(n\right)}$ 中的任意一个m次代数超曲面上。

定理2 ( $P_m^{\left(n\right)}$ 中插值适定结点组的添加代数超曲面法)

$A={\left\{q^{\left(i\right)}\right\}}_{i=1}^{e_m^{\left(n\right)}}$ 是 $P_m^{\left(n\right)}\left(n\ge 2\right)$ 的适定结点组，做一个不通过A中任何点的k次无重复分量的代数超曲面 $Q\left(x\right)=0$ ，任取超曲面 $Q\left(x\right)=0$ 上的m + k次插值适定结点组 $B\in I_{m+k}^n\left(Q\right)$ ，则 $A\cup B$ 必构成 $P_{m+k}^{\left(n\right)}$ 的插值适定结点组。

在高维空间中下面首先给出一个四维空间上构造四元多项式空间 $P_m^{(4)}$ 插值适定结点组的超四面体迭代法，主要研究结果如下：

定理3：在四维空间C⁴上做5个超平面 ${\pi }_i$ ，使其交成一个超四面体(如图1四维空间投影到三维空间的一个超四面体)，在超四面体的10条边上(不过顶点)分别取m − 1个互异点，在每个超平面所在的四个平面(不在边)上分别取沿平面的m-3次插值可解结点组，再在每个超平面 ${\pi }_i$ (不在平面和边)上分别取沿该超平面的m − 4次插值可解结点组。将沿超平面 ${\pi }_i$ 的m − 4次插值可解结点组记为 $A_i$ ，则：

(1) $A_i$ 加上超平面 ${\pi }_i$ 所在的四个平面中任意1个平面的m − 3次插值可解结点组构成 ${\pi }_i$ 的m − 3次插值可解结点组。

(2) $A_i$ 加上超平面 ${\pi }_i$ 所在的四个平面中任意2个平面的m − 3次插值可解结点组，再加上 ${\pi }_i$ 所在的六条边中任意1条边上的m − 1个互异点构成 ${\pi }_i$ 的m − 2次插值可解结点组。

(3) $A_i$ 加上超平面 ${\pi }_i$ 所在的四个平面中任意3个平面的m − 3次插值可解结点组，加上 ${\pi }_i$ 所在的六条边中任意3条边上的m − 1个互异点，再加上 ${\pi }_i$ 所在四个顶点中的任意1个顶点构成 ${\pi }_i$ 的m − 1次插值可解结点组。

(4) $A_i$ 加上超平面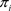所在的四个平面中全部平面的m − 3次插值可解结点组，加上 ${\pi }_i$ 所在的六条边中所有边上的m − 1个互异点，再加上 ${\pi }_i$ 所在的四个顶点构成 ${\pi }_i$ 的m次插值可解结点组。

如果用 $B_i\left(i=1,2,3,4,5\right)$ 表示(4)中所有点共同组成的点集，则：

定理4：如果 $B_0$ 表示超四面体外关于 $P_{m-5}^{\left(4\right)}$ 的一个m − 5次插值适定结点组，则 $B_0\cup B_1\cup B_2\cup B_3\cup B_4\cup B_5$ 必构成 $P_m^{\left(4\right)}$ 的插值适定结点组。

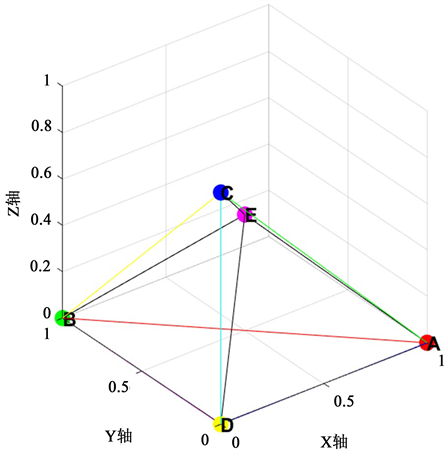
Figure 1. Projection of a hypertetrahedron in three dimensions

图1. 超四面体在三维空间的投影

3. 定理的证明

为了证明本文的研究结果，下面给出与定理3和定理4的证明有关的两个引理：

引理1 [6] ：在四维空间中，超平面 $\pi \left(X\right)=0$ 上的点组 ${\left\{Q_i\right\}}_{i=1}^{e_m^{\left(4\right)}\left(1\right)}$ 能够构成沿超平面 $\pi \left(X\right)=0$ 的m次插值适定结点组的充要条件是： $\forall g\left(X\right)\in P_m^{\left(4\right)}$ 且满足零插值条件 $g\left(Q_i\right)=0,i=1,\cdots ,e_m^{\left(4\right)}\left(1\right)$ ，都存在如下形式的分解：

$g\left(X\right)=\pi \left(X\right)r(\; X\; )$

其中，当 $m\ge 1$ 时， $r\left(X\right)\in P_{m-1}^{\left(4\right)}$ ，当 $m<1$ 时， $r\left(X\right)\equiv 0$ 。

引理2 [6] ：如果四维空间中两超平面 $h_1\left(X\right)=0$ 与 $h_2\left(X\right)=0$ 相交于一个四维空间中平面 $C=S\left(h_1,h_2\right)$ (C表示 $h_1\left(X\right)$ 与 $h_2\left(X\right)$ 公共零点的集合)，那么位于C上的点组 ${\left\{Q_i\right\}}_{i=1}^{e_m^{\left(4\right)}\left(1,1\right)}$ 能做成C的m次插值可解结点组的充要条件是： $\forall g\left(X\right)\in P_m^{\left(4\right)}$ 且满足零插值条件 $g\left(Q_i\right)=0,i=1,2,\cdots ,e_m^{\left(4\right)}\left(1,1\right)$ ，都存在如下形式的分解：

$g\left(X\right)=\alpha \left(X\right)h_1\left(X\right)+\beta \left(X\right)h_2(\; X\; )$

其中 $\alpha \left(X\right)\in P_{m-1}^{\left(4\right)}$ ， $\beta \left(X\right)\in P_{m-1}^{\left(4\right)}$ 。

引理1与引理2的证明分别与文献 [6] 中的引理3.1及引理2.9的证明类似。

定理3的证明：

先证明(1)，设 $A_1={\left\{Q_i\right\}}_{i=1}^{\frac{\left(m-1\right)\left(m-2\right)\left(m-3\right)}{6}}$ 是沿超平面 ${\pi }_1$ 的m − 4次插值适定结点组。取平面ABC上的 $\frac{\left(m-1\right)\left(m-2\right)}{2}$ 个点为 $A={\left\{Q_i\right\}}_{i=1}^{\frac{\left(m-1\right)\left(m-2\right)}{2}}$ ，则A构成沿平面 ${\pi }_1\cap {\pi }_2=ABC$ 上的m − 3次插值适定结点组。

对于 $\forall P\in P_{m-3}^{\left(4\right)}$ 且 $P\left(Q_i\right)=0,\forall Q_i\in A$ ，由引理2得 $P=\alpha {\pi }_1+\beta {\pi }_2$ ，又 $P\left(Q_i\right)=0,\forall Q_i\in A$ ，则 $P\left(Q_i\right)=\alpha \left(Q_i\right){\pi }_1\left(Q_i\right)+\beta \left(Q_i\right){\pi }_2\left(Q_i\right)=0$ 所以， $\beta \left(Q_i\right)=0,\forall Q_i\in A_1$ ，因为 $A_1$ 是沿超平面 ${\pi }_1$ 的m − 4次插值适定结点组， $\beta$ 为m − 4次多项式，那么由引理1可得 $\beta ={\pi }_{1}r$ 。

则 $P=\alpha {\pi }_1+{\pi }_{1}r{\pi }_2=\left(\alpha +r{\pi }_2\right){\pi }_1={\pi }_{1}r$ ，(1)得证，(2) (3) (4)同理可证，定理3证毕。

定理4的证明：

因为 $A_i$ 为超平面 ${\pi }_i$ 上的m − 4次插值可解结点组，又知 $B_0$ 是 $P_{m-5}^{\left(4\right)}$ 的一个m − 5次插值适定结点组，且超平面 ${\pi }_i$ 不通过 $B_0$ 中的点，由定理2可得 $B_0\cup A_i$ 必构成 $P_{m-4}^{\left(4\right)}$ 的插值适定结点组。

然后使用定理3中(1)的方法可得到超平面 ${\pi }_j\left(j\ne i\right)$ 上的一个m − 3次插值可解结点组，记为 $A_j$ ，则 $B_0\cup A_i\cup A_j$ 构成 $P_{m-3}^{\left(4\right)}$ 的插值适定结点组，重复以上的这个过程，并且继续使用定理3可以得到 $B_0\cup A_i\cup A_j\cup A_k\cup A_l\cup A_s\left(i\ne j\ne k\ne l\ne s;i,j,k,l,s=1,2,3,4,5\right)$ 这些点集必构成 $P_m^{\left(4\right)}$ 的插值适定结点组。

$B_0\cup A_i\cup A_j\cup A_k\cup A_l\cup A_s$ 中所含点恰好与 $B_0\cup B_1\cup B_2\cup B_3\cup B_4\cup B_5$ 中所含点相同，且所含点的个数都等于 $P_m^{\left(4\right)}$ 的维数，定理4证毕。

由此研究结果可以得到四维空间中单纯形上Lagrange插值的一个构造算法，进而可以推广到n维空间中单纯形上Lagrange插值的一个构造算法，如下所示。

4. 构造算法及具体实例

假设n维单纯形的n + 1个超平面表示为：

$\begin{array}{l}{S}_{1,0}\left(x_1,x_2,\cdots ,x_n\right)=a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n+a_{1,n+1}=0\\ S_{2,0}\left(x_1,x_2,\cdots ,x_n\right)=a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n+a_{2,n+1}=0\\ ⋮\\ S_{n,0}\left(x_1,x_2,\cdots ,x_n\right)=a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n+a_{n,n+1}=0\\ S_{n+1,0}\left(x_1,x_2,\cdots ,x_n\right)=a_{n+1,1}{x}_1+a_{n+1,2}{x}_2+\cdots +a_{n+1,n}{x}_n+a_{n+1,n+1}=0\end{array}$

用n + 1簇平行的超平面：

$\begin{array}{l}{S}_{1,i_1}\left(x_1,x_2,\cdots ,x_n\right)=a_{11}{x}_1+a_{12}{x}_2+\cdots +a_{1n}{x}_n+a_{1,n+1}+i_1\cdot h_1=0,i_1=0,1,2,\cdots ,m\\ S_{2,i_2}\left(x_1,x_2,\cdots ,x_n\right)=a_{21}{x}_1+a_{22}{x}_2+\cdots +a_{2n}{x}_n+a_{2,n+1}+i_2\cdot h_2=0,i_2=0,1,2,\cdots ,m\\ ⋮\\ S_{n,i_n}\left(x_1,x_2,\cdots ,x_n\right)=a_{n1}{x}_1+a_{n2}{x}_2+\cdots +a_{nn}{x}_n+a_{n,n+1}+i_n\cdot h_n=0,i_n=0,1,2,\cdots ,m\\ S_{n+1,i_{n+1}}\left(x_1,x_2,\cdots ,x_n\right)=a_{n+1,1}{x}_1+a_{n+1,2}{x}_2+\cdots +a_{n+1,n}{x}_n+a_{n+1,n+1}+i_{n+1}\cdot h_{n+1}=0,i_{n+1}=0,1,2,\cdots ,m\end{array}$

将单纯形作剖分。

用 $Q_{1i_1,2i_2,\cdots ,n{i}_n}\left(x_1,x_2,\cdots ,x_n\right)$ 表示为 $S_{1,i_1}\left(x_1,x_2,\cdots ,x_n\right)$ ， $S_{2,i_2}\left(x_1,x_2,\cdots ,x_n\right)$ ， $\cdots$ ， $S_{n,i_n}\left(x_1,x_2,\cdots ,x_n\right)$ 的交点， 则 ${\eta }_n=\left\{Q_{1i_1,2i_2,\cdots ,n{i}_n}|i_1=0,1,\cdots ,n;i_2=0,1,\cdots ,n-i_1;\cdots ;i_n=0,1,\cdots ,n-i_1-i_2-\cdots -i_{n-1}\right\}$ 构成 $P_m^{\left(n\right)}$ 的适定结点组。令：

$\begin{array}{l}{A}_{1,0}\left(x_1,x_2,\cdots ,x_n\right)\equiv 1;A_{1,i_1}\left(x_1,x_2,\cdots ,x_n\right)={\displaystyle \underset{l=0}{\overset{i_1-1}{\prod }}{S}_{1,l}\left(x_1,x_2,\cdots ,x_n\right)}\\ A_{2,0}\left(x_1,x_2,\cdots ,x_n\right)\equiv 1;A_{2,i_2}\left(x_1,x_2,\cdots ,x_n\right)={\displaystyle \underset{l=0}{\overset{i_2-1}{\prod }}{S}_{2,l}\left(x_1,x_2,\cdots ,x_n\right)}\\ ⋮\\ A_{n,0}\left(x_1,x_2,\cdots ,x_n\right)\equiv 1;A_{n,i_n}\left(x_1,x_2,\cdots ,x_n\right)={\displaystyle \underset{l=0}{\overset{i_n-1}{\prod }}{S}_{n,l}\left(x_1,x_2,\cdots ,x_n\right)}\\ A_{n+1,0}\left(x_1,x_2,\cdots ,x_n\right)\equiv 1;A_{n+1,i_{n+1}}\left(x_1,x_2,\cdots ,x_n\right)={\displaystyle \underset{l=0}{\overset{i_{n+1}-1}{\prod }}{S}_{n+1,l}\left(x_1,x_2,\cdots ,x_n\right)}\end{array}$

对应点 $Q_{1i_1,2i_2,\cdots ,n{i}_n}$ 的Lagrange插值基本多项式为：

$\begin{array}{l}{L}_{1i_1,2i_2,\cdots ,n{i}_n}\left(x_1,x_2,\cdots ,x_n\right)\\ =\frac{A_{1,i_1}\left(x_1,x_2,\cdots ,x_n\right)}{A_{1,i_1}\left(Q_{1i_1,2i_2,\cdots ,n{i}_n}\right)}\cdot \frac{A_{2,i_2}\left(x_1,x_2,\cdots ,x_n\right)}{A_{2,i_2}\left(Q_{1i_1,2i_2,\cdots ,n{i}_n}\right)}\cdot \cdots \cdot \frac{A_{n,i_n}\left(x_1,x_2,\cdots ,x_n\right)}{A_{n,i_n}\left(Q_{1i_1,2i_2,\cdots ,n{i}_n}\right)}\cdot \frac{A_{n+1,n-i_1-i_2-\cdots -i_{n-1}}\left(x_1,x_2,\cdots ,x_n\right)}{A_{n+1,n-i_1-i_2-\cdots -i_{n-1}}\left(Q_{1i_1,2i_2,\cdots ,n{i}_n}\right)}\end{array}$

得到 ${\eta }_n$ 上的Lagrange插值公式为：

$P\left(x_1,x_2,\cdots ,x_n\right)={\displaystyle \underset{0\le i_1+i_2+\cdots +i_n\le n}{\sum }f\left(Q_{1i_1,2i_2,\cdots ,n{i}_n}\right)L_{1i_1,2i_2,\cdots ,n{i}_n}\left(x_1,x_2,\cdots ,x_n\right)}$

具体算例：

由于我们无法直观地想象高维空间中的单纯形，在这里，我们举常用到的二维空间及三维空间中有关单纯形上Lagrange插值的具体例子。

例1：利用二维单纯形网格上的Lagrange插值公式构造如下多项式：三角形ABC为直角三角形(如图2)，被插值函数为 $f\left(x,y\right)=\frac{1}{x+y+1}$ ，构造出二元一次插值多项式。

Figure 2. Right-angled triangle ABC

图2. 直角三角形ABC

解：三角形ABC的3条边BC，AC，AB的方程分别为： $S_{10}=y;S_{20}=x+y-1;S_{30}=x$

取直角三角形ABC的三个插值结点(即三角形ABC的三个顶点)分别为：

$Q_{10，20}\left(1,0\right),Q_{10,21}\left(0,0\right),Q_{11，20}\left(0,1\right)$

则：

$\begin{array}{l}{A}_{10}\equiv 1;A_{11}=S_{10}=y;\\ A_{20}\equiv 1;A_{21}=S_{20}=x+y-1;\\ A_{30}\equiv 1;A_{31}=S_{30}=x\end{array}$

对应所取结点的Lagrange插值基本多项式分别为：

$L_{10，20}\left(x,y\right)=x;L_{10，21}\left(x,y\right)=1-x-y;L_{11，20}\left(x,y\right)=y$

函数 $f\left(x,y\right)$ 在所取结点处的函数值分别为： $f\left(Q_{10,20}\right)=\frac{1}{2};f\left(Q_{10,21}\right)=1;f\left(Q_{11,20}\right)=\frac{1}{2}$

得二元一次插值多项式： $P\left(x,y\right)=1-\frac{1}{2}x-\frac{1}{2}y$

经验证被插值函数 $f\left(x,y\right)$ 与所求多项式 $P\left(x,y\right)$ 在插值结点处的结果相等。取点 $\left(0,\frac{1}{2}\right)$ 及 $\left(\frac{1}{2},\frac{1}{2}\right)$ 进行验证，求得 $f\left(0,\frac{1}{2}\right)=\frac{2}{3}$ ， $P\left(0,\frac{1}{2}\right)=\frac{3}{4}$ ， $f\left(\frac{1}{2},\frac{1}{2}\right)=\frac{1}{2}$ ， $P\left(\frac{1}{2},\frac{1}{2}\right)=\frac{1}{2}$ ，在点 $\left(0,\frac{1}{2}\right)$ 处插值误差 $t_1=\left|\frac{2}{3}-\frac{3}{4}\right|=\frac{1}{12}\approx 0.083$ ，在点 $\left(\frac{1}{2},\frac{1}{2}\right)$ 处插值误差 $t_2=\left|\frac{1}{2}-\frac{1}{2}\right|=0$ 。

例2：给定四面体O-ABC，它的三个面OAB，OAC，OBC分别是直角三角形(如图3)，被插值函数为 $f\left(x,y,z\right)=\frac{1}{x+y+z+1}$ ，利用三维单纯形网格上的Lagrange插值公式，构造出三元二次插值多项式。

Figure 3. Tetrahedron O-ABC

图3. 四面体O-ABC

解：四面体O-ABC的四个面OBC，OAC，OAB，ABC的方程分别为：

$S_{10}=z;S_{20}=x;S_{30}=y;S_{40}=x+y+z-2$

用平行平面 $S_{11}=z-1;S_{21}=x-1;S_{31}=y-1;S_{41}=x+y+z-1$ 将该四面体作等距剖分，

取四面体O-ABC的十个插值结点分别为：

$Q_{10,20,30}\left(0,0,0\right),Q_{11,20,30}\left(0,0,1\right),Q_{10,21,30}\left(1,0,0\right),Q_{10,20,31}\left(0,1,0\right),Q_{11,21,30}\left(1,0,1\right)$

$Q_{11,20,31}\left(0,1,1\right),Q_{10,21,31}\left(1,1,0\right),Q_{10,20,32}\left(0,2,0\right),Q_{10,22,30}\left(2,0,0\right),Q_{12,20,30}\left(0,0,2\right)$

则：

$\begin{array}{l}{A}_{10}\equiv 1;A_{11}=S_{10}=z;A_{12}=S_{10}\cdot S_{11}=z\left(z-1\right);\\ A_{20}\equiv 1;A_{21}=S_{20}=x;A_{22}=S_{20}\cdot S_{21}=x\left(x-1\right);\\ A_{30}\equiv 1;A_{31}=S_{30}=y;A_{32}=S_{30}\cdot S_{31}=y\left(y-1\right);\\ A_{40}\equiv 1;A_{41}=S_{40}=x+y+z-2;A_{42}=S_{40}\cdot S_{41}=\left(x+y+z-2\right)\left(x+y+z-1\right)\end{array}$

对应所取结点的Lagrange插值基本多项式分别为：

$\begin{array}{l}{L}_{10,20,30}=\frac{1}{2}\left(x+y+z-2\right)\left(x+y+z-1\right);\\ L_{11,20,30}=-z\left(x+y+z-2\right);\\ L_{10,21,30}=-x\left(x+y+z-2\right);\\ L_{10,20,31}=-y\left(x+y+z-2\right);\\ L_{11,21,30}=xz;L_{11,20,31}=yz;L_{10,21,31}=xy;\\ L_{10,20,32}=\frac{y\left(y-1\right)}{2};L_{10,22,30}=\frac{x\left(x-1\right)}{2};L_{12,20,30}=\frac{z\left(z-1\right)}{2}\end{array}$

函数 $f\left(x,y,z\right)$ 在所取结点处的函数值分别为：

$\begin{array}{l}f\left(Q_{10,20,30}\right)=1;f\left(Q_{11,20,30}\right)=\frac{1}{2};f\left(Q_{10,21,30}\right)=\frac{1}{2};f\left(Q_{10,20,31}\right)=\frac{1}{2};f\left(Q_{11,21,30}\right)=\frac{1}{3};\\ f\left(Q_{11,20,31}\right)=\frac{1}{3};f\left(Q_{10,21,31}\right)=\frac{1}{3};f\left(Q_{10,20,32}\right)=\frac{1}{3};f\left(Q_{10,22,30}\right)=\frac{1}{3};f\left(Q_{12,20,30}\right)=\frac{1}{3}\end{array}$

得三元二次插值多项式：

$\begin{array}{c}P\left(x,y,z\right)=\frac{1}{2}\left(x+y+z-2\right)\left(x+y+z-1\right)-\frac{1}{2}z\left(x+y+z-2\right)-\frac{1}{2}x\left(x+y+z-2\right)\\ -\frac{1}{2}y\left(x+y+z-2\right)+\frac{1}{3}\left(xz+yz+xy\right)+\frac{1}{6}\left(x^2+y^2+z^2-x-y-z\right)\\ =\frac{1}{6}\left(x^2+y^2+z^2\right)-\frac{2}{3}\left(x+y+z\right)+\frac{1}{3}\left(xz+yz+xy\right)+1\end{array}$

经验证被插值函数 $f\left(x,y,z\right)$ 与所求多项式 $P\left(x,y,z\right)$ 在插值结点处的结果相等。取点 $\left(1,1,1\right)$ 及点 $\left(\frac{1}{2},\frac{3}{2},0\right)$ 进行验证，求得 $f\left(1,1,1\right)=\frac{1}{4}$ ， $P\left(1,1,1\right)=\frac{1}{2}$ ， $f\left(\frac{1}{2},\frac{3}{2},0\right)=\frac{1}{3}$ ， $P\left(\frac{1}{2},\frac{3}{2},0\right)=\frac{1}{3}$ ，在点 $\left(1,1,1\right)$ 处插值误差为 $k_1=\left|\frac{1}{2}-\frac{1}{4}\right|=\frac{1}{4}=0.25$ ，在点 $\left(\frac{1}{2},\frac{3}{2},0\right)$ 处插值误差为 $k_2=\left|\frac{1}{3}-\frac{1}{3}\right|=0$ 。

NOTES

^*通讯作者。