关于循环图C(10,3)的交叉点
On the Crossing Points of Circulant Graphs C(10,3)
DOI: 10.12677/AAM.2023.1212515, PDF, HTML, XML, 下载: 84  浏览: 125 
作者: 高 琳：辽宁师范大学数学学院，辽宁 大连
关键词: 交叉数；循环图；好画法；去边数；Crossing Number； Circulant Graph； Good Drawing； Removal Number
摘要: 众所周知，确定循环图交叉数的精确值是非常困难的。即便如此，在这一领域的一些重要结果仍然得到了证明。C(10,3)作为C(3m + 1,3) (m ≥ 3)这一类循环图的证明基础，本文证明了在C(10,3)的最优画法中，主圈上的边最多自交1次。
Abstract: It is well known that determining the exact values of crossing number for circulant graphs is very difficult. Even so, some important results in this field are still proved. C(10,3) as the basis for the proof of C(3m + 1,3) (m ≥ 3), in this paper, we prove that the edges from the principal circle of C(10,3) cross each other at most once in an optimal drawing.
文章引用：高琳. 关于循环图C(10,3)的交叉点[J]. 应用数学进展, 2023, 12(12): 5241-5253. https://doi.org/10.12677/AAM.2023.1212515

1. 引言

本文中所有的图都是简单图。术语和符号可以在 [1] [2] 中找到。在这里我们重复一些定义。循环图 G = C ( n ; S ) 是顶点集 V ( C ( n ; S ) ) = { v i | 0 ≤ i ≤ n − 1 } ，边集 E ( c ( n ; S ) ) = { v s v t | 0 ≤ s ≤ n − 1 ， 0 ≤ t ≤ n − 1 , ( s − t ) mod n ∈ S } ， S = { 1 , 2 , ⋯ , | n / 2 | } 的图。当 S = { 1 , k } 时，对于某些整数k，则 C ( n ; S ) 将被简化为 C ( n , k ) 。对于 C ( n , 3 ) ，环 C n = v 0 , v 1 , ⋯ , v n − 1 , v n , v 0 称为主圈。显然大多数类型的循环图都是非平面的。

图的一个画法是平面中的一种表示，使得其顶点由不同的点表示，其边由连接相应点对的简单连续弧表示。如果一个画法满足以下条件，它就是好的画法：(i) 没有边与自己相交；(ii) 两条边交叉不超过一次；(iii) 三条或三条以上的边不能交叉于一点；(iv) 没有边与顶点相交。一个交叉是两条边的共同的内部点。G的交叉数，写为 c r ( G ) ，是平面上G的所有好画法中交叉的最小值。图G的最优画法是交叉数等于 c r ( G ) 的一个好的画法。在一个好画法D中，如果一条边没有被任何其他边交叉，则称它在画法D中是干净的。否则，称它在画法D中被交叉。

Jordan曲线定理：任意一条简单(自身不相交)闭曲线J把平面分成两个区域，在不同区域的两点若要相连，则连结的弧必与J相交。

显然，当且仅当 c r ( G ) = 0 时，G是平面的。因此，交叉数被认为是图的一个重要拓扑测度。对于一个图来说，计算交叉数是NP完全的 [3] 。因此，只有对于非常有限的循环图类，交叉数的精确值才是已知的。据我们所知，Hao等人 [4] 的这篇文章是我们可以找到的关于这个主题的早期结果。然后H. Ren等人确定了一些 C ( m , 3 ) 的交叉数 [5] [6] 。同时，验证了当 m > 3 时， C ( 3 m , m ) 的交叉数的精确值为m [7] 。2007年，这一结果被扩展到 C ( 3 m + 1 , m ) [8] 。结果表明，当 m > 3 时， c r ( C ( 3 m + 1 , m ) ) = m + 1 。尽管这些确切的数字得到了证实，但这些交叉点是由哪些边相交得到的仍然未知。在本文中，我们证明出在 C ( 10 , 3 ) 的最优画法中，其主圈上的边最多自交1次。事实上，对广义Petersen图和笛卡尔图的类似研究工作也出现在许多论文中。感兴趣的读者可以参考 [9] [10] [11] [12] 了解更多详细信息。

2. 基础引理和主要结果

在这一部分中，我们首先定义证明过程中需要用到的概念及符号，其次列出几个关于 C ( 10 , 3 ) 的引理和本文的目标定理。

C ( 10 , 3 ) 的主圈是环 v 0 v 1 ⋯ v 9 v 0 ，为了便于叙述，用H0表示主圈 v 0 v 1 ⋯ v 9 v 0 ；边 v s v t 称为弦，其中 s + 3 = t ( mod 10 ) , s = 0 , 1 , ⋯ , 9 。为了讨论方便我们用Bs表示弦 v s v t 其中 s + 3 = t ( mod 10 ) , s = 0 , 1 , ⋯ , 9 。例如 B 0 = v 0 v 3 ， B 1 = v 1 v 4 。 B s , t = B s ∪ B s + 1 ∪ B s + 2 ∪ ⋯ ∪ B t 。同时我们可以给 C ( 10 , 3 ) 上色。具体地，主圈H0中的边被分配蓝色，用b表示；弦被指定为红色，用r表示。按照定义，主圈自交n次可以叙述为有n个b-b交点，类似地，n条弦交主圈可以描述为有n个r-b交点，因为一条边只有一个交点。图G的去边数是非负整数，记作 h ( G ) ，如果从图G中最少删去h条边就能得到图G的平面子图，那么 h ( G ) = h 。

引理1 ( [7] ) 对于循环图 C ( 10 , 3 ) ， c r ( C ( 10 , 3 ) ) = 4 且 h ( C ( 10 , 3 ) ) ≥ 4 。

由引理1容易得到下面的引理。

引理2 令D是 C ( 10 , 3 ) 的一个最优画法，那么没有边被交2次。

证明：根据去边数的定义可知 c r ( C ( 10 , 3 ) ) ≥ h ( C ( 10 , 3 ) ) ，又由引理1可得到 4 ≥ h ( C ( 10 , 3 ) ) ≥ 4 。因此， h ( C ( 10 , 3 ) ) = 4 。假设存在一条边可以被交两次，那么删除3条边就能得到平面图，与 h ( C ( 10 , 3 ) ) = 4 矛盾，所以一条边不能被交2次。

引理3 ( [13] ) 如果主圈上的边自交产生n个交点，那么这n个交点将主圈分成n + 1个部分。

将n个交点连成一条线(直线或曲线)，这条线将 S i ( i = 1 , 2 , ⋯ , n + 1 ) 分割成上下两侧。如图1所示，是主圈自交产生n个交点时，主圈的n + 1个部分。

Figure 1. Good drawings of H0 with n crossing points

图1. 有n个交叉点的H0的好的画法

引理4 ( [13] ) 在所有的Si中，两端的Si上至少有一个顶点，内部Si上下两侧，每侧至少有一个顶点。

定理5 在 C ( 10 , 3 ) 的最优画法中主圈最多可以自交1次。

3. 定理5的证明

证明：用反证法。因为 c r ( C ( 10 , 3 ) ) = 4 ，我们要证主圈最多自交一次，所以需要分3种情形讨论即分别讨论 C ( 10 , 3 ) 的最优画法有4，3，2个b-b交点时是否与 c r ( C ( 10 , 3 ) ) = 4 矛盾。

设D是 C ( 10 , 3 ) 的最优画法，当D有4个b-b交点时，由引理3和引理4可知S1和S5上至少有1个顶点， S 2 , S 3 , S 4 的两侧，每侧至少有1个顶点，因此我们能够确定8个顶点的位置，还有2个顶点的位置没确定。定义这两不确定位置的顶点为剩余点，用N表示剩余点的数量。当D有4个b-b交点时， N = 2 。如果两个剩余点都在某个Si上，记作 N i = 2 ，类似地，如果Si上有1个剩余点，记作 N i = 1 。现在我们讨论 N = 2 时，这两个剩余点的位置。因为主圈自交时，主圈的最优画法具有对称性，当 C ( 10 , 3 ) 有4个b-b交点时，S1和S5是对称的，所以我们只需讨论在其中一个 S i ( i = 1 , 5 ) 上的情形即可。类似地， S i ( i = 2 , 3 , 4 ) 的两侧也是对称的。因为图 C ( 10 , 3 ) 是自同构的，任意的顶点 v i ( i = 0 , 1 , ⋯ , 9 ) 都可能在S1上，所以不失一般性设v0在S1上。下面我们将分成3个情形讨论。

3.1. C(10,3)有4个b-b交点

由引理3可知，将H0分成5个部分即 S i ( i = 1 , 2 , 3 , 4 , 5 ) 。由引理4可知 N = 2 ，可分成2个剩余点在一个Si上还是在两个Si上共两种情况进行讨论。

3.1.1. 两个剩余点在同一个Si (i = 1, 2, 3, 4, 5)上

情形1 两点在S1或S5上

不失一般性设两点在S1上。因为4个交点已出现，所以B1是干净的， H 0 ∪ B 1 与图2同构，有B2交 H 0 ∪ B 1 ，产生5个交点，与 c r ( C ( 10 , 3 ) ) = 4 矛盾。

情形2 两点在S2或S4上

不失一般性设两点在S2上。分成S2两侧剩余点数之比为0:2和1:1两种情形讨论。显然B1是干净的，当S2两侧剩余点数之比为0:2时， H 0 ∪ B 1 与图3同构，有B6交 H 0 ∪ B 1 ，产生5个交点，与 c r ( C ( 10 , 3 ) ) = 4 矛盾。当S2两侧剩余点数之比为1:1时， H 0 ∪ B 1 与图4同构，有B2交 H 0 ∪ B 1 ，产生5个交点，矛盾。

Figure 2. Good drawings of H 0 ∪ B 1

图2. H 0 ∪ B 1 的好的画法

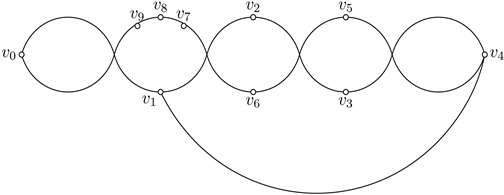
Figure 3. Good drawings of H 0 ∪ B 1

图3. H 0 ∪ B 1 的好的画法

Figure 4. Good drawings of H 0 ∪ B 1

图4. H 0 ∪ B 1 的好的画法

情形3 两点在S3上

分成S3两侧剩余点数之比为0:2和1:1两种情形讨论。显然B1是干净的，当S2两侧剩余点数之比为0:2时， H 0 ∪ B 1 与图5同构，有B6交 H 0 ∪ B 1 ，产生5个交点，矛盾。

S2两侧剩余点数量之比为1:1的情形也可用类似方法得到矛盾。

3.1.2. 两个剩余点在2个Si (i = 1, 2, 3, 4, 5)上

按照两点分别在S1和S2，S1和S3，S1和S4，S1和S5，S2和S3，S2和S4共6种情形讨论。注意当两点分别在S2和S3时，又有两点在S2和S3的同侧和异侧两种子情形，在S2和S4这种情形也是如此。我们这里只讨论两点分别在S1和S2上时，因为4个交点已出现，所以B1是干净的， H 0 ∪ B 1 与图6同构。有B2交 H 0 ∪ B 1 ，产生5个交点，矛盾。剩余5种情形可以用类似方法证明。

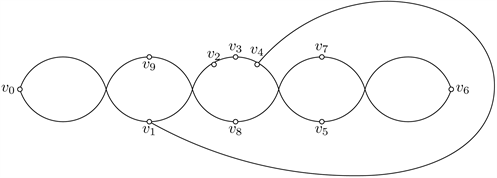
Figure 5. Good drawings of H 0 ∪ B 1

图5. H 0 ∪ B 1 的好的画法

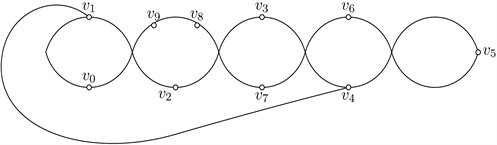
Figure 6. Good drawings of H 0 ∪ B 1

图6. H 0 ∪ B 1 的好的画法

3.2. C(10,3)有3个b-b交点

由引理4可知 N = 4 ，这4个剩余点可能分布在一个，两个，三个或四个Si上。证明方法和思路类似，我们这里只讨论4个剩余点在同一个 S i ( i = 1 , 2 , 3 , 4 ) 上。

3.2.1. 4个剩余点在S1或S4上

不失一般性，假设4个点在S1上。如果没有r-b交点， H 0 ∪ B 3 与图7同构，有B4和B9交B3，与引理2矛盾。所以 { B 3 , B 4 , B 9 } 中有且只有一条边上存在r-b交点。4个交点已出现，所以B7是干净的，有B2交 H 0 ∪ B 7 ，产生5个交点，矛盾。

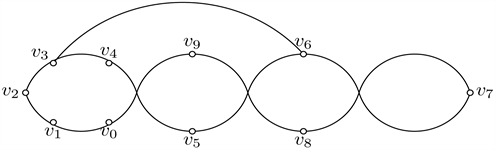
Figure 7. Good drawings of H 0 ∪ B 7

图7. H 0 ∪ B 7 的好的画法

3.2.2. 4个剩余点在S2或S3上

不失一般性，设在4个点在S2上。S2两侧剩余点数之比可能为0:4，1:3或2:2。当S2两侧剩余点数之比为0:4时，如果没有r-b交点， H 0 ∪ B 9 与图8同构，有B4和B3交B9，与引理2矛盾。所以 { B 3 , B 4 , B 9 } 中有且只有一条边上存在r-b交点。4个交点已出现，所以B0是干净的，有B8交 H 0 ∪ B 0 ，产生5个交点，矛盾。当S2两侧剩余点数之比为1:3时，如果没有r-b交点， H 0 ∪ B 7 与图9同构，有S2和B3交B7，与引理2矛盾。所以 { B 3 , B 2 , B 7 } 中有且只有一条边上存在r-b交点。4个交点已出现，所以B6和B9干净， H 0 ∪ B 6 ∪ B 9 与图10同构，有B8交 H 0 ∪ B 6 ∪ B 9 ，产生5个交点，矛盾。可用类似方法证明剩余情况。

Figure 8. Good drawings of H 0 ∪ B 9

图8. H 0 ∪ B 9 的好的画法

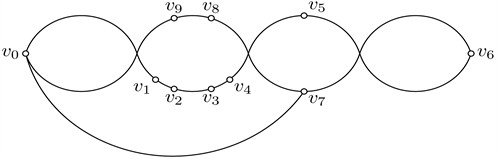
Figure 9. Good drawings of H 0 ∪ B 7

图9. H 0 ∪ B 7 的好的画法

Figure 10. Good drawings of H 0 ∪ B 6 ∪ B 9

图10. H 0 ∪ B 6 ∪ B 9 的好的画法

3.3. C(10,3)有2个b-b交点

由引理3可知 C ( 10 , 3 ) 分成3个部分， S 1 , S 2 , S 3 。由引理4可知 N = 6 ，下面讨论这6个剩余点的位置。这6个点可能在一个，两个或三个 S i ( i = 1 , 2 , 3 ) 上。这里只讨论6个点在1个Si上，其他情况可以用类似方法证明，这里就不一一列举。

3.3.1. 6个剩余点在S1或S3上

不失一般性，设这6个点在S1上。H0与图11同构。如果不存在r-b交点，有B4和B5交B9，与引理2矛盾，所以 { B 4 , B 5 , B 9 } }中至少有一条边上有r-b交点。如果B9没有r-b交点，那么B4和B5交 H 0 ∪ B 9 ，4个交点已出现，所以B2和B3是干净的，v4在环 v 2 v 5 v 6 v 3 v 2 所围成的区域之中，B1交 H 0 ∪ B 2 , 3 ，出现5个交叉点，矛盾。所以B9有r-b交点。如果 { B 4 , B 5 } 中存在一条边上有r-b交点，那么4个交点已出现，B2和B3是干净的，v4在环 v 2 v 5 v 6 v 3 v 2 所围成的区域之中，有B1交 H 0 ∪ B 2 , 3 ，出现5个交叉点，矛盾。所以B4和B5没有r-b交点。 H 0 ∪ B 4 , 5 与图12同构。有B8交 H 0 ∪ B 4 , 5 ，4个交点已出现，所以B2干净，有B3交 H 0 ∪ B 4 , 5 ∪ B 2 ，产生5个交点，矛盾。

Figure 11. Good drawings of H0

图11. H0的好的画法

Figure 12. Good drawings of H 0 ∪ B 4 , 5

图12. H 0 ∪ B 4 , 5 的好的画法

3.3.2. 6个剩余点都在S2上

情形1 S2两侧剩余点数量之比为0:6

假设没有r-b交点，有B0和B7交B9，与引理2矛盾，所以 { B 0 , B 7 , B 9 } 中至少有1条边上有r-b交点。显然B9上一定有r-b交点，否则B0和B7交 H 0 ∪ B 9 ，4个交点已出现，所以B2和B3干净， H 0 ∪ B 2 , 3 与图13同构，有B1交 H 0 ∪ B 2 , 3 ，产生5个交点，矛盾。如果 { B 0 , B 7 } 中存在一条边上有r-b交点，那么4个交点已出现，所以B2、B3干净，有B1交 H 0 ∪ B 2 , 3 ，产生5个交叉点，矛盾。所以B0和B7干净， H 0 ∪ B 7 ∪ B 0 与图14同构。有B2交 H 0 ∪ B 7 ∪ B 0 ，4个交点已出现，所以B6干净，有B8交 H 0 ∪ B 0 ∪ B 6 , 7 。产生5个交点，矛盾。

Figure 13. Good drawings of H 0 ∪ B 2 , 3

图13. H 0 ∪ B 2 , 3 的好的画法

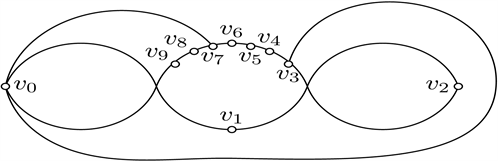
Figure 14. Good drawings of H 0 ∪ B 7 ∪ B 0

图14. H 0 ∪ B 7 ∪ B 0 的好的画法

情形2 S2两侧剩余点数量之比为1:5

假设没有r-b交点，那么 H 0 ∪ B 7 ∪ B 0 ∪ B 3 与图15同构。如果B1上有r-r交点，那么B1交B0和B3，与引理2矛盾，所以B1上没有r-r交点， H 0 ∪ B 7 ∪ B 0 , 1 ∪ B 3 与图16同构，有B2交B1且B9交B0，4个交点已出现，所以B6干净。有B8交B6，产生5个交点，矛盾。所以 { B 3 , B 7 , B 0 , B 1 , B 2 , B 9 , B 8 , B 6 } 中至少有一条边有r-b交点。如果 { B 3 , B 0 , B 1 , B 2 , B 9 } 中存在2条边上同时有r-b交点，那么B7和B8干净，如图17所示，B6交 H 0 ∪ B 7 , 8 ，产生5个交点，矛盾。所以当 { B 3 , B 0 , B 1 , B 2 , B 9 } 中存在一条边上有r-b交点时，另外4条边上不能有r-b交点。

如果 { B 0 , B 1 , B 9 } 中的一条边有r-b交点，那么B3和B2上都不能有r-b交点，如果B2交B3，那么4个交点已出现，B7和B8干净， H 0 ∪ B 7 , 8 与图17同构，有B6交 H 0 ∪ B 7 , 8 ，产生5个交点，矛盾，所以B2与 H 0 ∪ B 3 不交。 H 0 ∪ B 2 , 3 与图18同构，有B4交 H 0 ∪ B 2 , 3 ，4个交点已出现，所以B7和B8干净，有B6交 H 0 ∪ B 7 , 8 ∪ B 2 , 3 ，产生5个交点，矛盾。所以B0，B1和B9上都没有r-b交点，进而 H 0 ∪ B 0 与图19同构。

Figure 15. Good drawings of H 0 ∪ B 7 ∪ B 0 ∪ B 3

图15. H 0 ∪ B 7 ∪ B 0 ∪ B 3 的好的画法

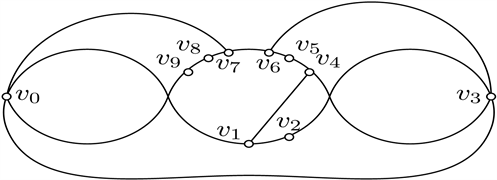
Figure 16. Good drawings of H 0 ∪ B 7 ∪ B 0 , 1 ∪ B 3

图16. H 0 ∪ B 7 ∪ B 0 , 1 ∪ B 3 的好的画法

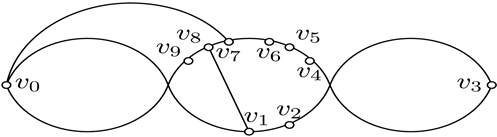
Figure 17. Good drawings of H 0 ∪ B 7 , 8

图17. H 0 ∪ B 7 , 8 的好的画法

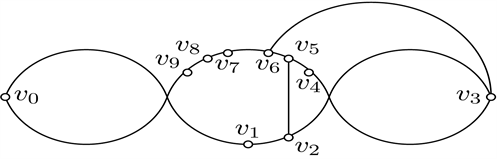
Figure 18. Good drawings of H 0 ∪ B 2 , 3

图18. H 0 ∪ B 2 , 3 的好的画法

Figure 19. Good drawings of H 0 ∪ B 0

图19. H 0 ∪ B 0 的好的画法

由引理2可知， { B 1 , B 9 } 中最多有一条边交B0。如果B1交B0，那么B9与 H 0 ∪ B 0 , 1 不交，有B3和B8交 H 0 ∪ B 0 , 1 ∪ B 9 ，产生5个交点，矛盾。所以B1与 H 0 ∪ B 0 不交。 H 0 ∪ B 0 , 1 与图20同构，有B2和B9交 H 0 ∪ B 0 , 1 ，4个交点已出现，所以B7和B8干净，有B6交 H 0 ∪ B 7 , 8 ∪ B 0 , 1 ，产生5个交点，矛盾。

Figure 20. Good drawings of H 0 ∪ B 0 , 1

图20. H 0 ∪ B 0 , 1 的好的画法

情形3 S2两侧剩余点数量之比为2:4

假设无r-b交点，那么 H 0 ∪ B 0 ∪ B 7 ∪ B 4 与图21同构，因为B1交B0和引理2，所以B0不能再被交叉，因此B8是干净的，如图22中所示。有B6和B9交 H 0 ∪ B 0 ∪ B 7 , 8 ∪ B 4 ，产生5个交点，矛盾。所以 { B 0 , B 7 , B 4 , B 1 , B 8 } 中至少有一条边上有r-b交点。如果 { B 7 , B 4 , B 8 } 中存在两条边上同时有r-b交点，4个交点已出现，那么B0干净，有B1交 H 0 ∪ B 0 ，产生5个交叉点，矛盾。因此，如果 { B 7 , B 4 , B 8 } 中任意一条边上有r-b交点，那么另外两条边上一定没有r-b交点。

如果B7有r-b交点，那么B4无r-b交点， H 0 ∪ B 4 与图23同构。如果B2交 H 0 ∪ B 4 ，那么4个交点已出现，B0干净，有B1交 H 0 ∪ B 0 ∪ B 4 ，产生5个交点，矛盾。所以B2与 H 0 ∩ B 4 不交。 H 0 ∪ B 4 ∪ B 2 与图24同构。有B3交 H 0 ∪ B 2 ∪ B 4 ，4个交点已出现，所以B0干净，有B1交 H 0 ∪ B 0 ∪ B 4 ，产生5个交点，矛盾。因此B7没有r-b交点。根据对称性可知，B4也没有r-b交点。

假设B8存在r-b交点，如果B3有r-b交点，那么4个交点已出现，B0干净，有B1交 H 0 ∪ B 0 ，产生5个交点，矛盾。所以B3与 H 0 ∪ B 7 ∪ B 4 不交， H 0 ∪ B 7 ∪ B 3 , 4 与图25同构。有B2交 H 0 ∪ B 7 ∪ B 3 , 4 ，4个交点已出现，所以B0干净，有B1交 H 0 ∪ B 7 ∪ B 3 , 4 ∪ B 0 ，产生5个交点，矛盾。因此B8没有r-b交点。所以 { B 0 , B 1 } 中至少有一条边上有r-b交点。如果B0和B1都有r-b交点，那么4个交点已出现，B3干净， H 0 ∪ B 7 ∪ B 3 , 4 与图25同构，有B2交 H 0 ∪ B 7 ∪ B 3 , 4 ，产生5个交点，矛盾。所以 { B 0 , B 1 } 中有且只有一条边上有r-b交点。

Figure 21. Good drawings of H 0 ∪ B 0 ∪ B 7 ∪ B 4

图21. H 0 ∪ B 0 ∪ B 7 ∪ B 4 的好的画法

Figure 22. Good drawings of H 0 ∪ B 0 ∪ B 7 , 8 ∪ B 4

图22. H 0 ∪ B 0 ∪ B 7 , 8 ∪ B 4 的好的画法

Figure 23. Good drawings of H 0 ∪ B 4

图23. H 0 ∪ B 4 的好的画法

Figure 24. Good drawings of H 0 ∪ B 4 ∪ B 2

图24. H 0 ∪ B 4 ∪ B 2 的好的画法

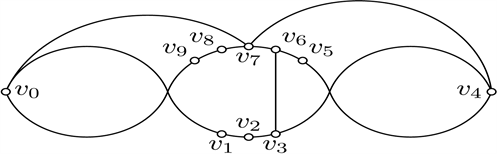
Figure 25. Good drawings of H 0 ∪ B 7 ∪ B 3 , 4

图25. H 0 ∪ B 7 ∪ B 3 , 4 的好的画法

因为B0和B1对称，不失一般性，假设B1有r-b交点，那么B0没有， H 0 ∪ B 7 ∪ B 4 ∪ B 0 与图26同构。显然B3与 H 0 ∪ B 7 ∪ B 4 ∪ B 0 不交，否则4个交点已出现，B8干净，有B9交B8，产生5个交点，矛盾。因此，有B2交 H 0 ∪ B 7 ∪ B 3 , 4 ∪ B 0 ，产生5个交点，矛盾。所以，B1没有r-b交点。又根据对称性，B0也没有r-b交点，与 { B 0 , B 1 } 中有且只有一条边有r-b交点矛盾。

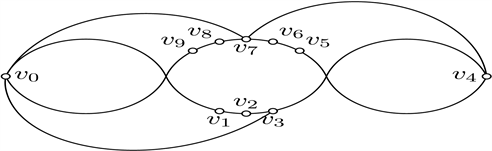
Figure 26. Good drawings of H 0 ∪ B 7 ∪ B 4 ∪ B 0

图26. H 0 ∪ B 7 ∪ B 4 ∪ B 0 的好的画法

情形4 S2两侧剩余点数量之比为3:3

如果没有r-b交点， H 0 ∪ B 7 ∪ B 0 与图27同构。有B7交B5，B0交B2，4个交点已经出现。所以B6干净，有B8交B6，产生5个交点，矛盾。因此 { B 7 , B 0 } 中至少存在一条边上有r-b交点。

如果B7和B0上都存在r-b交点，4个交点已出现，所以B2，B5和B3干净， H 0 ∪ B 2 , 3 ∪ B 5 与图28同构。有B1交 H 0 ∪ B 2 , 3 ∪ B 5 ，产生5个交点，矛盾。所以 { B 7 , B 0 } 中有且只有一条边上存在r-b交点。

如果B7上有r-b交点，那么B0上不存在r-b交点。 H 0 ∪ B 0 与图29同构，有B2交 H 0 ∪ B 0 ，4个交点已经出现，所以B1是干净的。此时，B2交 H 0 ∪ B 0 , 1 ，产生5个交叉点，矛盾。因此，B7上没有r-b交点。又由对称性可知，B0上也没有r-b交点，与 { B 7 , B 0 } 中有且只有一条边上存在r-b交点矛盾。

综上所述，3.3证明完毕。

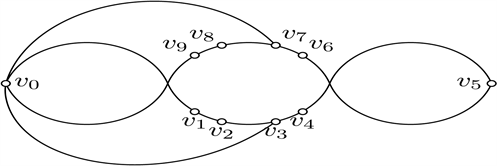
Figure 27. Good drawings of H 0 ∪ B 7 ∪ B 0

图27. H 0 ∪ B 7 ∪ B 0 的好的画法

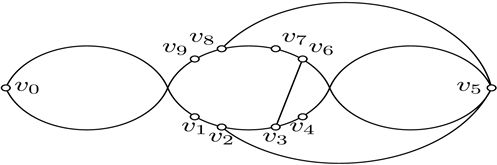
Figure 28. Good drawings of H 0 ∪ B 2 , 3 ∪ B 5

图28. H 0 ∪ B 2 , 3 ∪ B 5 的好的画法

Figure 29. Good drawings of H 0 ∪ B 0

图29. H 0 ∪ B 0 的好的画法

3.4. C(10,3)有1个b-b交点

C ( 10 , 3 ) 有1个b-b交点的最优画法如图30所示。

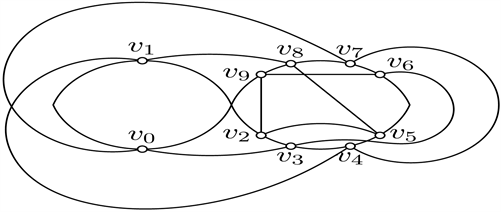
Figure 30. Good drawings of C ( 10 , 3 ) with a b-b crossing point

图30. 有1个b-b交点的 C ( 10 , 3 ) 好的画法

4. 结论

对于循环图 C ( 10 , 3 ) 交叉点的性质，本文证明当 C ( 10 , 3 ) 的主圈分别自交4次，3次，2次时， C ( 10 , 3 ) 的最优画法中的交叉数都与 c r ( C ( 10 , 3 ) ) = 4 矛盾。因为 C ( 10 , 3 ) 的交叉数是4，所以其主圈最多自交4次，进而得到结论 C ( 10 , 3 ) 的最优画法中主圈最多自交1次。

参考文献

[1] Bondy, J.A. and Murty, U.S.R. (1976) Graph Theory with Applications. Macmilan Ltd. Press, New York.
[2] Mohar, B. and Thomassen, C. (2001) Graphs on Surfaces. Johns Hopkins University Press, Baltimore.
https://doi.org/10.56021/9780801866890
[3] Garey, M.R. and Johnson, D.S. (1983) Crossing Number Is NP-Complete. SIAM Journal on Algebraic Discrete Methods, 4, 312-316.
https://doi.org/10.1137/0604033
[4] Hao, R.X. and Liu, Y.P. (1999) New Upper Bounds on Crossing Number of Circular Graph. OR Transactions, 3, 1-6.
[5] Lu, J.J., Ren, H. and Ma, D.J. (2004) On the Crossing Number of C(m, 3). Journal of Systems Science and Mathematical Sciences, 24, 504-512.
[6] Lu, J.J., Wu, Y.R. and Ren, H. (2005) Crossing Number of Certain Circular Graphs. Journal of East China Normal University, 16-22.
[7] Lin, X.H., Yang, Y.S., Lv, J.G. and Hao, X. (2005) The Crossing Number of C(mk;{1, k}). Graphs and Combinatorics, 21, 89-96.
https://doi.org/10.1007/s00373-004-0597-5
[8] Ho, P.T. (2007) The Crossing Number of the Circular Graph C(3k + 1;{1, k}). Discrete Mathematics, 307, 2771-2774.
https://doi.org/10.1016/j.disc.2007.02.001
[9] McQillan, D. and Richter, R.B. (1992) On the Crossing Numbers of Certain Generalized Petersen Graphs. Discrete Mathematics, 104, 311-320.
https://doi.org/10.1016/0012-365X(92)90453-M
[10] Richter, R.B. and Salazar, G. (2002) The Crossing Number of P(N, 3). Graphs and Combinatorics, 18, 381-394.
https://doi.org/10.1007/s003730200028
[11] Székely, L.A. (2004) A Successful Concept for Measuring Non-Planarity of Graphs: The Crossing Number. Discrete Mathematics, 276, 331-352.
https://doi.org/10.1016/S0012-365X(03)00317-0
[12] Salazar, G. (2005) On the Crossing Numbers of Loop Net-works and Generalized Petersen Garaphs. Discrete Mathematics, 302, 243-253.
https://doi.org/10.1016/j.disc.2004.07.036
[13] Lu, W., Li, F., Ren, H., et al. (2023) On the Crossing Points of Circulant Graphs C(9, 3). International Journal of Mathematics and Systems Science, 6, 206-211.

为你推荐