1. 引言
若一个图G有一棵支撑树T (树T是无圈连通图且树T与图G的顶点集相同)使得支撑树T的最大顶点度至多为k,则称此树T是图G的一棵支撑k-树。图的支撑树特征问题一直是结构图论中一个重要的研究课题。该问题的产生和发展与结构图论中著名的哈密尔顿问题的研究密切相关,因此受到国内外许多图论专家的关注。若非平凡的图中存在一条哈密尔顿路(经过图中每个顶点恰好一次的路),则该图中存在恰好两个叶子的支撑树且最大度至多为2。这很自然地引出了如下问题:给出保证图中存在至多k个叶子的支撑树或者支撑k-树的条件。目前在图中是否存在具有和哈密尔顿性相关的特征的支撑树问题的研究主要从参数的角度进行刻画,运用独立数、连通度、邻域并、度和等条件,集中讨论图中是否存在以下五类特征的支撑树的充分条件:1) 图中存在支撑k-树;2) 图中存在至多k个叶子的支撑树;3) 图中存在至多k个分支点的支撑树;4) 给定连通度条件下,
-free图中存在至多k个叶子的支撑树;5) 图中存在以任意k个顶点作为叶子集(树中度为1的顶点的集合)的支撑树。
支撑树在网络中也有具体的应用。比如,当网络中存在物理环路时,会导致广播风暴,会产生巨大的网络流量,极其容易造成交换机死机。现在是一个信息化飞速发展的时代,企业网络在设计时往往对网络稳定性的要求比较高,要求其网络架构多点互联,多机热备。支撑树技术能够在二层交换网中保证企业网络多点互联,同时也能够避免出现交换网络中的环路。此外,支撑树的计数或者限定条件的支撑树的计数也是图论研究中的一个热门问题。
2. 预备知识
在这篇文章中,我们只考虑有限无向简单图,对于一些没有给出的术语和符号可以参考文献 [1] 。设G为一个有限无向简单图,用
和
分别表示图G的顶点集和边集。定义
和
分别为图G的阶数和边数。对于
,
表示顶点v在图G中的邻点的集合。
表示顶点v在图G中关联的边的数目,定义为顶点v在图G中的度。一般地,
和
分别简记为
和
。对于顶点集
,
表示为顶点集X的基数。符号
表示以X为顶点集,以图G中两端点均在X中的边的全体为边集所构成的子图,称为X在G中的导出子图。
表示从图G中删除边
得到的图,
表示从图G中增添边
得到的图。对于两个图G和H,
表示为图G和图H的并,即令图G和图H中顶点集的并和边集的并分别作为
的顶点集和边集。记
和
。定义
和
,其中整数
。
对于顶点集
,若X中任意两顶点在图G中均不相邻,则称X为G的一个独立顶点集。图G中最大独立顶点集的基数称为独立数,记为
。对于一个整数
,当
时,我们定义
以及
,否则定义
。显然,
。完全图是指图G中的任意两点均有连边,
表示阶数为n的完全图。二部图又称二分图,是指一个图G,其顶点集
可分解为两个互不相交的非空子集A和B,并且图中的每条边所关联的两个顶点分别属于这两个不同的顶点集A和B。记二部图G为
,此时也称
为图G的一个二分类。若图G为具有二分类
的简单二部图,且分部A中每个顶点都与B中每个顶点相连,则称图G为完全二部图。若
,
,则记图
为
。常见的完全二部图
称为爪。如果图G中不含同构于H的导出子图,则称图G是H-free图。特别地,若图G是
-free图,则称其为无爪图。
连通无圈的图称为树,通常用符号T表示。若树T包含图G中的所有顶点,则称T为图G的支撑树。树T中度数为1的顶点称为树T的叶子,树T中度数至少为3的顶点称为树T的分支点。符号
表示起点为u且终点为v的路,其长度等于路中边的条数。特别地,由于树T是连通无圈的,连接T中任意两顶点u和v的路是唯一确定的,用符号
表示。符号
表示顶点u和顶点v在树T中的距离。
经过图G中每个顶点恰好一次的路称为图G的一条哈密尔顿路。关于哈密尔顿路的许多研究都基于下面Ore [2] 的结果。
定理1 [2] 令图G是阶数为n的连通图。若
,则图G中存在一条哈密尔顿路。
显然,一条非平凡的哈密尔顿路都含有恰好两个叶子。对于图G中含至多有限个叶子的支撑树问题,主要从参数角度,利用度和、独立数、邻域并等条件进行了研究。最早,Win在 [3] 中得到了一个关于独立数条件的结论。
定理2 [3] 令图G是k-连通图。对于整数
,若
,则图G中存在至多m个叶子的支撑树。
Broersma和Tuinstra在 [4] 中考虑了度和条件,得到了下面的定理。
定理3 [4] 令图G是阶数为n的连通图。对于整数
,若
,则图G中存在至多m个叶子的支撑树。
Flandrin等学者在 [5] 中利用邻域并得到了一个关于图中存在至多k个叶子的支撑树的充分条件。
定理4 [5] 令图G是阶数为n的连通图。对于整数
,若
,则图G中存在至多k个叶子的支撑树。
对于连通无爪图,Kano在 [6] 中以及陈晓东在 [7] 中分别给出了下面的定理。
定理5 [6] 令图G是阶数为n的连通无爪图。对于整数
,若
,则图G中存在至多m个叶子的支撑树。
定理6 [7] 令图G是阶数为n的k-连通无爪图。若
,则图G中存在至多3个叶子的支撑树。
对于连通
-free图,Kyaw [8] [9] 给出了下面两个定理。
定理7 [8] 令图G是阶数为n的连通
-free图。若
,则图G中存在至多3个叶子的支撑树。
定理8 [9] 令图G是阶数为n的连通
-free图。
1) 若
,则图G中存在哈密尔顿路;
2) 若
,其中
,则图G中存在至多m个叶子的支撑树。
对于包含至多k个分支点的支撑树问题,Gargano等学者在 [10] 中研究了连通无爪图和
-free图中存在至多k个分支点的支撑树的充分条件,并说明了结论中的界是最好可能的。Matsuda等学者在 [11] 中分别利用独立数条件和度和条件得到了下面两个结论,并且说明了结论中的界是最好可能的。
定理9 [11] 令图G是连通无爪图。若
,则图G中存在至多k个分支点的支撑树。
定理10 [11] 令图G是阶数为n的连通无爪图。若
,则图G中存在至多1个分支点的支撑树。
对于连通
-free图,陈园在 [12] 中证明了下面这个定理。
定理11 [12] 令图G是阶数为n的连通
-free图。若
,则图G中存在至多4个叶子的支撑树。
受到上面这些结果的启发,在这篇文章中,我们考虑了邻域并条件来确保阶数为n的连通
-free图G中存在至多3个叶子的支撑树,得到了下面的结果。
定理12:令图G是阶数为n的连通
-free图。若
,则图G中存在至多3个叶子的支撑树。
显然,如果一个树至多有k(
)个叶子,那么这个树至多有
个分支点。因此,我们可以直接得到下面的推论。
推论13:令图G是阶数为n的连通
-free图,若
,则图G中存在至多1个分支点的支撑树。
下面我们举例来说明定理12中的邻域并条件“
”是最好可能的。对于
,设H1,H2,H3,H4是4个顶点不交的完全图
,xy是一条边并且顶点x和y都不在顶点集
中。如图1所示,令图G是通过连接x和
中的所有顶点以及y和
中的所有顶点所得到的图。显然,图G是一个连通
-free图,图G的顶点数目
以及
。但是,图G的每个支撑树都至少有4个叶子。

Figure 1. An infinite family of connected
-free graphs G having no span ning tree with at most 3 leaves
图1. 不存在至多3个叶子的支撑树的连通
-free图类
3. 主要结果的证明
为了完成证明,我们需要用到下面这个引理。
引理14 [8] :设图G是一个连通图使得图G中不存在至多3个叶子的支撑树且T是图G中含有4个叶子的最大树,那么图G中不存在至多3个叶子的树
使得
。
定理12的证明:我们用反证法来证明此定理。假设图G不存在至多3个叶子的支撑树,选取图G中包含4个叶子的最大树T,令集合
是T中度为1的顶点的集合。根据T的选择,我们有
。因为T含有4个叶子,所以T中至多含有两个分支点。下面我们根据T的分支点的个数进行分类讨论。
情形1:T包含2个分支点。
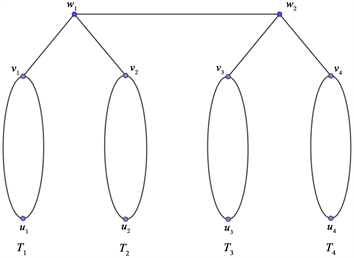
Figure 2. A maximal tree T of G with 4 leaves
图2. 图G中包4个叶子的最大树T
如图2所示,设
和
是T中的两个分支点使得
。对于
,令
是
的连通分支的顶点集使得
,
是集合
中的唯一顶点。不失一般性,不妨设
,
。对于
,
和
分别表示x在
(或者
)上的前继顶点和后继顶点。
和
分别表示
上
的后继顶点和
的前继顶点。定义
。在情形1中,我们选取T使得
尽可能小,其中
是顶点
和
在T中的距离。
断言1:如果
,那么
,
并且
。
证明:设
,则
对于某些
。不失一般性,不妨设
。若
,则图G中存在树
使得
有3个叶子并且
,这与引理14的结论矛盾。若
,则图G中存在树
使得
有3个叶子并且
,这与引理14的结论矛盾。若
,则存在
使得
,此时图G中存在树
使得
有3个叶子并且
,与引理14的结论矛盾。□
断言2:
。
证明:假设断言2不成立,即存在点
使得
。不失一般性,不妨设
,则图G中存在树
使得
有4个叶子并且
,此时
有两个分支点
和x,
,以及
,这与T的选取矛盾。□
断言3:
。
证明:假设
,则由断言1可得
以及
,此时图G中存在导出子图
,这与图G是
-free图矛盾。假设
,不失一般性,不妨设
,则存在一个点顶
使得
以及
。若
,即
,则图G中存在树
使得
有3个叶子并且
,这与引理14的结论矛盾;若
,则存在顶点
使得
。因为T的选取使得
尽可能小,所以
,此时图G中存在导出子图
,这与图G是
-free图矛盾。□
对于
,由断言1可知
,
,
和
是
中两两互不相交的子集,其中
,所以
因此,
. (1)
显然,
.
定义
,根据断言2得,
.
因此,
. (2)
综合(1) (2)两式可得,
由于
,所以
.
这与定理1中的条件
矛盾。
情形2:T包含1个分支点。
设r是T的分支点使得
。因为图G是
-free图,所以存在不同的
使得
。令
,如果
是叶子,那么
是G中含有3个叶子的树使得
,这与引理14的结果矛盾。所以假设
,那么
是G中含有4个叶子的树使得
,此时
有两个分支点r和
,且
,这与情形1类似,同样可以得出矛盾。
综上,对于阶数为n的连通
-free图G,如果
,那么图G中存在至多3个叶子的支撑树。■
4. 总结
图的结构问题的研究是图论研究中的热点领域,其中图中存在给定特征的支撑树是结构图论中重要的研究课题。众所周知,判定一个图是否含有一条哈密尔顿路从算法复杂性来讲是NP-完全的。对于图G,给图G的每个顶点均加上
条悬挂边得到图
,显然图
中存在支撑k-树的充要条件是图G中含有一条哈密尔顿路。类似地,任取图G中一个顶点v,在顶点v上增添
条悬挂边得到图
,显然图
中存在至多k个叶子的支撑树的充要条件是图G中含有一条哈密尔顿路。于是图中是否存在支撑k-树或至多k个叶子的支撑树问题也是NP-完全的 [13] 。所以对于诸类问题的研究主要集中在给出判定一个图是否含有上述特征支撑树的充分条件。2009年,Kyaw在 [8] 中给出了
-free图中存在至多3个叶子的支撑树的度和条件。Flandrin等学者在 [5] 中利用邻域并得到了一个关于图中存在至多k个叶子的支撑树的充分条件。受到这些结果的启发,在这篇文章中我们考虑了邻域并条件来确保阶数为n的连通
-free图G中存在至多3个叶子的支撑树,且该条件的下界是最好可能的。
本文在解决问题的过程中,首先通过构造一个反例图类(不存在至多3个叶子的支撑树的连通
-free图类),计算出该图类中任意4个独立顶点的邻域并的基数,然后猜测确保连通
-free图存在至多3个叶子的支撑树的邻域并条件最好的下界形式,最后我们通过反证法证明定理12中的邻域并条件是最好可能的。在定理12的证明过程中,对于给定的图G,我们假设图G不存在至多3个叶子的支撑树,选取图G中包含4个叶子的最大树T,通过计算树T的阶数
,建立其与图G中4个独立顶点的邻域并的基数之间的数量关系,很显然有
,从而得到了与定理12中给定邻域并条件相矛盾的结果,完成了主要结果的证明。
基金项目
国家自然科学基金(12101126)。