基于Logistic回归和局部多项式回归的疾病风险预测

Disease Risk Prediction Based on Logistic Regression and Local Polynomial Regression

摘要: 出血性脑卒中一种危险的神经系统疾病，由脑部血管破裂引起出血，病情急剧进展，病死率高，对患者和社会带来沉重负担。因此，研究出血性脑卒中的诊疗至关重要，可改善患者预后、减少残疾和死亡率，提高医疗系统效率和质量。本文利用Logistic回归、局部多项式回归对血肿扩张和血肿周围水肿两个指标建模，研究出血性脑卒中患者血肿扩张风险、血肿周围水肿发生及演进规律，最终结合临床和影像信息，预测出血性脑卒中患者的临床预后，并据此优化临床决策。

Abstract: Hemorrhagic stroke is a dangerous neurological disease with bleeding caused by rupture of a blood vessel in the brain, which is rapidly progressive and has a high mortality rate, imposing a heavy burden on patients and society. Therefore, it is crucial to study the diagnosis and treatment of hemorrhagic stroke to improve patient prognosis, reduce disability and mortality, and improve the efficiency and quality of the healthcare system. In this paper, we used Logistic regression and local polynomial regression to model two indicators, hematoma expansion and perihematoma edema, to study the risk of hematoma expansion, the occurrence and evolution of perihematoma edema in hemorrhagic stroke patients, and finally to predict the clinical prognosis of hemorrhagic stroke patients by combining clinical and imaging information, and to optimize clinical decision-making accordingly.

1. 引言

脑卒中是一种严重的神经系统疾病，通常是由于脑部的血液供应中断或血管破裂而引起的，是一种紧急情况，需要迅速识别和治疗，因为它可能导致严重的后果，包括永久的脑损伤甚至死亡。而出血性脑卒中是脑卒中较为严重的情况，它是由于脑部血管破裂导致的出血而引起的。出血性脑卒中起病急、进展快，预后较差，急性期内病死率高达45%~50%，约80%的患者会遗留较严重的神经功能障碍，同时也具有高复发性特征。上述严重的临床后果对患者生命和生活质量的影响很大，因此，预防、早期诊断和有效治疗对于减轻出血性脑卒中带来的负担至关重要。因为它有助于改善患者的预后、减少残疾和死亡率，同时也有助于提高医疗系统的效率和质量。

血肿扩张和血肿周围水肿的发生及发展是出血性脑卒中的两个关键事件，它们提供了关于病变严重程度、患者预后和治疗效果的关键信息。出血性脑卒中后，血肿范围扩大是预后不良的重要危险因素之一，短时间内，血肿范围可能因脑组织受损、炎症反应等因素逐渐扩大，导致颅内压迅速增加，从而引发神经功能进一步恶化，甚至危及患者生命。因此，通过监测血肿扩张的速度和程度，研究人员和医生可以更好地了解出血性脑卒中的病理生理过程。此外，血肿周围的水肿作为脑出血后继发性损伤的标志，在近年来引起了临床广泛关注。血肿周围的水肿可能导致脑组织受压，进而影响神经元功能，使脑组织进一步受损，进而加重患者神经功能损伤。通过对血肿周围水肿的研究有助于理解脑组织对于出血性损伤的反应，同时也为设计治疗策略提供了依据。因此，监测和控制血肿及血肿周围水肿的扩张是临床关注的一个重点。

医学影像技术的飞速进步，为无创动态监测出血性脑卒中后脑组织损伤和演变提供了有力手段。本文通过对真实临床数据的分析，研究出血性脑卒中患者血肿扩张风险、血肿周围水肿发生及演进规律，最终结合临床和影像信息(见图1脑出血患者CT平扫)，预测出血性脑卒中患者的临床预后，并据此优化临床决策具有重要的临床意义。

总之，研究出血性脑卒中的临床诊疗对于提高患者的生存率、康复机会和生活质量具有重要意义。这项工作有助于医疗界更好地了解如何应对这种严重的神经系统疾病，以及如何改善患者的护理和治疗。这也有助于推动医学进步，改进医疗实践，为患者提供更好的医疗服务。

2. 数据介绍

本文所用数据采用2023年中国研究生数学建模竞赛E赛题提供的医学影像数据。该数据包括160例(100例训练数据集 + 60例独立测试数据集)出血性脑卒中患者的个人史、疾病史、发病及治疗相关信息、多次重复的影像学检查(CT平扫)结果及患者预后评估。对于影像学检查数据，包括各个时间点血肿/水肿的体积、位置、形状特征及灰度分布等信息。

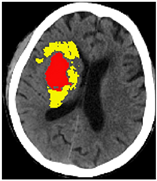
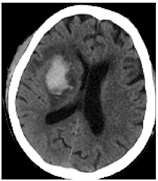(a) (b)

Figure 1. (a) The patient with cerebral hemorrhage has a CT plain scan; (b) The red is the hematoma, and the yellow is the edema around the hematoma

图1. 左图(a)脑出血患者CT平扫；右图(b)红色为血肿，黄色为血肿周围水肿

经过数据处理，形成样本量为160，变量个数为18的患者个人信息数据集1，变量包括发病到首次检查时间、年龄、性别、血压、吸烟史、饮酒史、高血压病史、卒中病史、糖尿病史、房颤史、冠心病史、脑室引流、止血治疗、降颅压治疗、降压治疗、镇静镇痛治疗、止吐护胃和营养神经，其中年龄、发病到首次检查时间与血压为连续型数据，其余皆为二元离散型数据，表示为1和0。

患者影像信息血肿及水肿的体积及位置数据是样本量为160，变量个数为22的数据集2。包含160名患者多次检查每个时间点血肿(Hemo)总体积及水肿(ED)总体积及不同位置的占比。此数据集中患者随访次数最多为6次，最少为3次，数据全部为连续型。

对于患者影像信息血肿及水肿的形状及灰度分布包含了每个时间点血肿及水肿的形状及灰度特征，灰度特征是基本的度量值，能够反映目标区域内体素强度的分布(17个字段)；形状特征是对目标区域三维形状的描述(14个字段)，得到样本量为160，变量个数为31的数据集3，数据全部为连续型。此数据只给出了流水号信息并未标注患者，后续研究数据需进行自行提取对应。

3. 基于Logistic回归预测血肿扩张

本节要研究48小时内发生血肿扩张概率，首先根据首次检查数据信息判断48小时内血肿是否扩张并构建Logistic模型预测所有患者发生血肿扩张的概率。具体建模步骤如下：

1) 判断患者是否发生血肿扩张事件获取更新后的数据集。

2) 划分训练集和测试集，将训练集的个人史、疾病史和首次影像特征整理为自变量X (利用随机森林筛选相关性高的20个指标)；将训练集的血肿扩张标记(1或0)作为目标变量。

3) 对自变量和目标变量进行Logistic回归拟合，使用极大似然估计获得变量系数 $b_0,b_1,\cdots ,b_n$ 。

4) 根据拟合模型对测试集进行预测，最后进行模型评价。

3.1. 选择Logistic回归的依据

Logistic回归作为一种广泛应用于分类问题的统计学习方法，它具有高度解释性特征，让我们能够理解每个特征对分类结果的影响程度，这有助于解释模型的决策过程。其次，逻辑回归在训练和预测速度迅速，特别适用于处理大规模数据集。同时又对异常值不敏感，不容易受到极端值的影响。此外，逻辑回归通常不需要对指示变量(也称为二元变量或虚拟变量)进行额外的处理，因为逻辑回归模型的数学表达能够有效地处理它们。因此，我们选用Logistic模型进行建模。

Logistic回归模型的构建

假设有一个特征向量X包含n个特征，以及对应的权重向量W，还有一个偏置项b。一般线性回归的模型可以表示为：

$Z=b+{\displaystyle {\sum }_{i=1}^n{W}_i{X}_i}$

其中：z是线性组合的结果。 $W_i$ 是第i个特征的权重。 $X_i$ 是第i个特征的取值。b是偏置项。然后，将z代入Sigmoid函数中，得到分类为1的概率 $P\left(Y=1|X\right)$ ：

$P\left(Y=1|X\right)=\frac{1}{1+{\text{e}}^{-Z}}$

相应地，分类为0的概率 $P\left(Y=0|X\right)$ 为：

$P\left(Y=0|X\right)=\frac{{\text{e}}^{-Z}}{1+{\text{e}}^{-Z}}$

这两个概率之和总是等于1，因为样本要么属于类别1，要么属于类别0。逻辑回归模型通过最小化损失函数来拟合训练数据，常用的损失函数是交叉熵损失函数。通过梯度下降等优化算法来找到最优的权重W和偏置项b，使得模型的预测尽可能接近实际标签。

3.2. 数据预处理

由于数据类型不同且数量不同，首先需要对数据进行统计，进行异常值处理和数据转换。

3.2.1. 数值计算

针对患者各个随访时间点相应的水肿体积数据，将随访时间点转化为与发病时间之间的时间间隔数据，获得“发病与每次检查之间的时间间隔”数据集。部分数据见表1：

Table 1. The time interval between onset and each examination

表1. 发病与每次检查之间的时间间隔

由于有些患者没有进行随访，表中时间数据为空值。

3.2.2. 数据提取对应

由于血肿扩张数据只给出了患者每次检查的流水号信息，并未明确标记患者信息，要对应患者信息进行血肿数据提取对应。

3.3. 血肿扩张判断

判断48小时内血肿发生情况

判断48小时内血肿是否发生，可以根据血肿体积前后变化，具体地说，当后续检查比首次检查绝对体积增加 ≥ 6 mL或相对体积增加 ≥ 33%即可认为发生血肿扩张。

首先对符号进行定义，见表2：

Table 2. Symbol definition

表2. 符号定义

定义变量：发病到首次影像检查时间间隔为O，每个患者的首次影像检查时的血肿体积(HM volume)记为 $X_0$ ，第n次随访时的血肿体积记为 $X_n$ 。

计算每个患者的血肿体积差值 ${\hat{\Delta }}_i$ ：

${\hat{\Delta }}_i=X_i-X_0,i=1,\cdots ,8$

如果 $X_i$ 不存在则输出一个空值。

血肿扩张指标：后续检查比首次检查绝对体积增加 ≥ 6 mL或相对体积增加 ≥ 33%。

将首次影像检查时间以及后续随访检查时间筛选出来满足血肿扩张的患者对应编号，再计算发生血肿扩张时的时间距离首次影像检查时的时间，再加上刚才定义的时间T，如果大于48则继续输出空值，小于48则输出结果。

显然我们可以得到 $V{D}_{i\left(j\right)}$ 和 $T{D}_{i\left(j\right)}$ 的计算公式为：

$V{D}_{i\left(j\right)}=V_{i\left(j\right)}-V_{i(\; 0\; )}$

$T{D}_{i\left(j\right)}=T_{i\left(j\right)}-T_{i(\; 0\; )}$

以下是判断第i个患者是否在发病48时内发生血脉扩张的算法流程图，见图2：

判断是否发生血肿主要用到发病到首次检查时间，各时间点血肿体积(HM_volume)，后续随访影像检查时间，利用Python计算各时间点血肿体积与首次检查体积变化差值，对比指标得到最终结果。具体结果见表3，这里只展示部分数据：

综合分析血肿扩张结果表格，前100名患者中在48小时内发生血肿扩张的共计22人，血肿发生时间处于6~41小时之间，平均血肿发生时间为21.18小时。

Figure 2. Algorithm flowchart

图2. 算法流程图

Table 3. Hematoma dilatation

表3. 血肿扩张情况

3.4. 基于特征筛选的扩张概率模型

3.4.1. 基于随机森林的特征选择

由于数据类型及指标较多，我们需要对其进行筛选，选择出与血肿发生高度相关的指标进行建模。对于预处理的数据中众多数值型特征进行特征筛选，这里方法选用随机森林 [1] [2] ，随机森林是一种强大的机器学习算法，它通常提供高度准确的预测性能，能够有效地降低过拟合风险，并处理高维数据集。此外，随机森林对异常值和噪声有较高的容忍度，易于使用，可并行化处理，适用于多种任务。基于特征重要性，共筛选了与血肿扩张相关的20个指标。

特征筛选的特征重要性见图3：

3.4.2. 基于Logistic回归模型的扩张概率

利用随机森林所选指标构造模型，基于因变量血肿扩张概率和自变量(20个相关性指标，即 $n=20$ )，构建Logistic回归模型 [3] [4] [5] ：

$P\left(Y=1|X\right)=\frac{1}{1+{\text{e}}^{-\left(b_0+b_1{x}_1+\cdots +b_n{x}_n\right)}}$

最终通过逻辑回归构建回归模型计算血肿扩张概率结果，预测的概率部分结果显示见表4，实际预测概率与血肿扩张情况基本一致。

Figure 3. Importance of features

图3. 特征重要性

Table 4. Probability of hematoma dilatation

表4. 血脉扩张概率

3.4.3. 模型评价

针对分类效果，我们要通过分类性能指标进行评估。在介绍评估指标之前首先介绍混淆矩阵，混淆矩阵见表5：

Table 5. Confusion matrix

表5. 混淆矩阵

由表可知：TP + FP + TN + FN等于样本总数，TP + FN为实际正样本数，FP + TN为实际负样本数。根据混淆矩阵可以计算出下列指标：

1) 召回率(True Positive Rate)：分类器正确分类的正样本数与真实样本数的比值，值越大说明分类效果越好。

$\text{Recall}=\frac{\text{TP}}{\text{TP}+\text{FN}}$

上式表示分类器对正例分类的效果，在类别非常不均衡也具有较好的后果。

2) 误报率(False Positive Rate)：分类器错误分类的样本数与真实样本数的比值，值越小说明分类效果越好。

3) ROC曲线 [6] (Receiver Operating Characteristic curve)

ROC曲线是用于评估二元分类模型性能的图形工具，它显示了模型在不同阈值下的召回率(True Positive Rate)与误报率(False Positive Rate)之间的关系。ROC曲线越靠近左上角，表示模型性能越好。

4) AUC (Area Under the ROC Curve)

AUC是ROC曲线下面积的度量，用于量化模型性能，AUC越接近1表示模型性能越好，0.5表示随机分类器，1表示完美分类器。

ROC曲线和AUC是评估分类模型性能的重要工具，尤其适用于处理类别不平衡问题。通过对Logistic回归模型结果评估，得到ROC曲线。此预测模型的ROC曲线见图4。ROC曲线下面积(AUC)：0.8945。通过指标评估可以看出通过Logistic回归预测血肿扩张是有效可行的。

Figure 4. ROC curve

图4. ROC曲线图

当发生出血性脑卒中时，应注重检测血肿扩张是否发生，患者48小时内发生血肿扩张较多，要做到及时检测及干预，抓住治疗的黄金时间。

4. 基于局部多项式回归拟合水肿体积进展曲线

局部多项式回归是一种非参数化的回归方法，它通过在数据集的不同局部区域上拟合多项式来建模数据。相对于全局多项式回归，局部多项式回归关注于数据的局部结构，从而更灵活地捕捉数据中的非线性关系。在局部权重的计算中，通常使用核函数来衡量一个点相对于拟合点的距离。常用的核函数包括高斯核和二次核。这些核函数赋予距离拟合点较近的数据点更高的权重，而远离点则权重逐渐减小。总体而言，局部多项式回归是一种适用于非线性和局部结构的回归方法，它在某些情况下能够更好地捕捉数据的特征，但需要小心调整带宽参数以避免过度拟合或欠拟合。因此，通过局部多项式回归拟合水肿体积进展曲线在理论上可行。

本节基于局部多项式回归建立水肿体积及时间拟合曲线，并利用多项式方法分析不同治疗方法对水肿体积进展模式的影响，最后利用皮尔森相关系数计算不同治疗方法下血肿体积、水肿体积之间的线性相关关系，并进行对比，进而考察不同治疗方法对水肿、血肿体积之间相关关系的影响。

4.1. 局部多项式回归的构建

考虑到所讨论的数据在X轴0点左侧无观测点，因此所拟合的曲线应当在边界处拟合误差较小的局部多项式拟合。

已知观测样本集 ${\left\{x_i,y_i\right\}}_{i=0}^N$ ， $x_i$ 表示发病到影像检查时间间隔(单位：小时h)， $y_i$ 表示水肿体积(单位：10⁻³ ml)，拟合采用多项式模型：

$\phi \left(x\right)={\displaystyle \underset{n=0}{\overset{M}{\sum }}{a}_n}{\phi }_n=a_0{\phi }_0\left(x\right)+\cdots +a_M{\phi }_M(\; x\; )$

其中 ${\phi }_0\left(x\right)=1$ 和 ${\phi }_n\left(x\right)=x^n,n=1~M$ 。

采用M阶多项式模型来求加权最小二乘解，就是求每个观测点 $x_i$ 的加权最小二乘解，其损失函数表达式为：

$\begin{array}{c}{J}_i\left(\theta \right)={\displaystyle \underset{x_j\in {\mathbb{N}}_i}{\sum }K\left(x_i,y_j\right)}{\left[y_j-{\displaystyle \underset{n=0}{\overset{M}{\sum }}{a}_n\left(x_i\right)x_j^n}\right]}^2\\ ={\displaystyle \underset{x_j\in {\mathbb{N}}_i}{\sum }K\left(x_i,y_j\right)}{\left[y_j-{\theta }_i^{\text{T}}\varphi \left(x_j\right)\right]}^2\end{array}$

${\theta }_i={\left[a_0\left(x_i\right),\cdots ,a_p\left(x_p\right)\right]}^{\text{T}},\varphi \left(x\right)={\left[1,x,x^2,\cdots ,x^p\right]}^{\text{T}}$

$k_h\left(x_i,y_i\right)=K_h\left(\Vert x-x_i\Vert \right)$ 为高斯核函数，用于刻画目标点 $x_i$ 的邻域位置 $x\in {{\rm N}}_i=\left\{x|\Vert x-x_i\Vert <\delta \right\}$ 处观测数据的权值，作为加权最小二乘解中的权值。通过求使损失函数达到最小的 $\theta$ 作为 $\theta$ 的估计值，其目标函数形式为

$\hat{\theta }\left(x\right)=\underset{\theta }{\min }{\displaystyle \underset{i=1}{\overset{N}{\sum }}{\left\{y_i-{\theta }_0-{\theta }_1\left(x_i-x\right)-\cdots -{\theta }_1{\left(x_p-x\right)}^p\right\}}^2{K}_h\left(x-x_i\right)}$

根据加权最小二乘估计可以得到 $2\hat{\theta }$ ，

$\hat{\theta }=X^{\text{T}}WX-X^{\text{T}}WY$

其中，

$x=\left(\begin{array}{cccc}1& x_1-x& \cdots & {\left(x_1-x\right)}^p\\ 1& x_2-x& \cdots & {\left(x_2-x\right)}^p\\ ⋮& ⋮& \ddots & ⋮\\ 1& x_n-x& \cdots & {\left(x_N-x\right)}^p\end{array}\right)$ ， $y=\left(\begin{array}{c}{y}_1\\ y_2\\ ⋮\\ y_N\end{array}\right)$ ， $W=\left(\begin{array}{cccc}{K}_h\left(x-x_1\right)& 0& \cdots & 0\\ 0& K_h\left(x-x_2\right)& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & K_h\left(x-x_N\right)\end{array}\right)$

4.2. 窗宽选择对水肿体积进展模式影响分析

由于带宽参数的选择会影响拟合效果，因此要比对不同带宽选择的拟合曲线。利用160名患者每次随访数据拟合曲线，利用局部多项式方法拟合所得全体患者水肿体积随时间进展模式在窗宽选择分别为20、50、100、150的情况下的拟合曲线见图5，数据中存在异常点(4307.583, 72247)，具体含义为第81号病人在第四次随访时的水肿体积检查结果，在此处为了优化曲线拟合效果，对此异常点采取删除处理，获得新的拟合数据集。在获得新的拟合数据集的基础上，利用局部多项式方法拟合所得新数据集中患者水肿体积随时间进展模式，在窗宽选择分别为20、50、100、150的情况下的拟合曲线图5(b)。

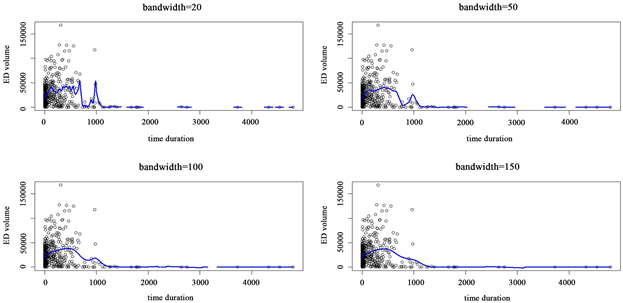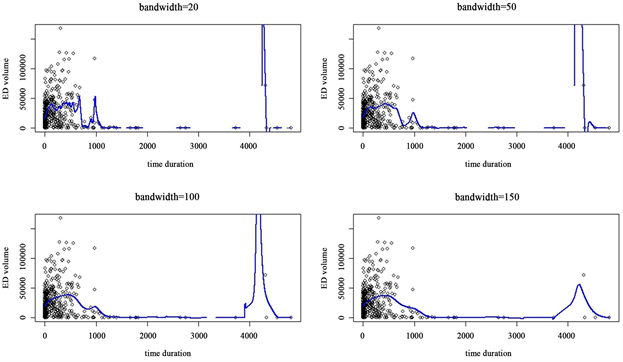(a)(b)

Figure 5. (a), (b) Progress model fitting diagram

图5. (a)、(b)进展模式拟合图

基于对不同窗宽对比可知，当窗宽选择为100时，拟合曲线效果较好，因此选取窗宽为100的局部多项式回归方法，所得具体拟合所得进展模式见图6：

Figure 6. Progression model fitting diagram

图6. 进展模式拟合图

4.3. 残差计算

在统计学和机器学习中，残差是指观测值与模型预测值之间的差异。通过分析残差，我们可以对模型的性能和拟合程度进行评估，并检测模型是否存在系统性的预测错误。残差计算公式如下：

$\overline{re{s}_i}=\frac{{\displaystyle \underset{j\in n_i}{\sum }re{s}_j}}{n_i},i=1,\cdots ,100$

其中， $n_i$ 表示每位患者的随访次数。通过计算结果，所得全体患者不同时间点下的水肿体积拟合曲线残差见图7，计算出残差可知在时间间隔在200小时至1000小时之间，曲线拟合残差呈现先增加后减少的态势。

Figure 7. Residual plot

图7. 残差图

5. 治疗方法对血肿体积、水肿体积影响

进一步的，为了讨论血肿体积、水肿体积和治疗方法之间的相关性，首先讨论全体患者血肿体积与水肿体积之间的相关关系，计算pearson相关系数，绘制相关关系图像，Pearson相关系数的计算公式：

${\rho }_{X,Y}=\frac{\mathrm{cov}\left(X,Y\right)}{{\sigma }_X{\sigma }_Y}=\frac{E\left[\left(X-EX\right)\left(Y-EY\right)\right]}{{\sigma }_X{\sigma }_Y}=\frac{E\left(XY\right)-E\left(X\right)E\left(Y\right)}{\sqrt{E\left(X^2\right)-E^2\left(X\right)}\sqrt{E\left(Y^2\right)-E^2(\; Y\; )}}$

其中X为血肿体积，Y 为水肿体积。全体患者水肿体积与血肿体积之间的相关关系图见图8：

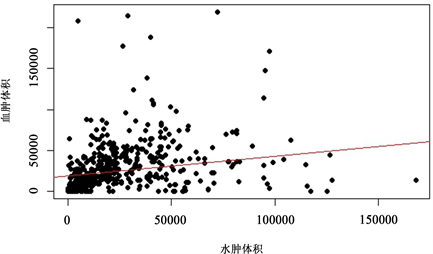
Figure 8. The correlation between edema volume and hematoma volume in all patients

图8. 全体患者水肿体积与血肿体积之间的相关关系图

在此基础上，讨论在不同治疗方案下的血肿体积与水肿体积的相关关系，分别计算在七种不同治疗方案下血肿体积与水肿体积之间的pearson相关系数，并绘制相关性图像，七种不同治疗方案下，水肿体积与血肿体积之间的相关系数见表6：

Table 6. Correlation coefficient between edema volume and hematoma volume under different treatment methods

表6. 不同治疗方法下水肿体积与血肿体积之间的相关系数

通过上述相关关系哦比较分析，可以得到当患者采用脑房引流治疗方法时，水肿体积与血肿体积之间的线性相关关系较强，由此可知，脑房引流治疗方法对于患者血肿体积和水肿体积影响较大，在临床治疗中应注重此治疗手段。

6. 总结与展望

脑卒中是一种危险的神经系统疾病，常因脑部血液供应中断或血管破裂引发，具有严重的后果，如永久脑损伤或死亡。血肿扩张和血肿周围水肿作为出血性脑卒中的两个关键事件，需得到监测和控制。通过本文研究，可知采用随机森林算法进行特征筛选，利用Logistic回归模型构建出血肿发生概率预测模型，结果预测准确率高，也从一定程度上反映出血肿扩张这一指标在判断和治疗出血性脑卒中具有重要意义。在对患者进行一段时间治疗后，检测多次随访数据，基于局部多项式回归建立水肿体积及时间拟合曲线，所拟合的曲线结果显示水肿体积随时间进展模式呈现先增长后下降的趋势，说明患者采取的治疗手段对水肿体积控制较为有效，因此，通过水肿体积可以作为衡量患者治疗的预后效果的一项指标。

通过多项式方法分析不同治疗方法对水肿体积进展模式的影响，结果显示脑房引流对其影响最为显著；利用皮尔森相关系数计算不同治疗方法下血肿体积、水肿体积之间的线性相关关系，并进行对比，进而考察不同治疗方法对水肿、血肿体积之间相关关系的影响，结果都说明脑房引流治疗方法下，水肿体积与血肿体积之间的相关关系较强。所以在出血性脑卒中的治疗过程中要重视这一治疗手段的应用。因此，通过真实临床数据分析，研究血肿扩张风险和血肿周围水肿演变规律，结合临床和影像信息，预测患者预后，将对临床决策产生积极影响。

总之，通过统计方法研究出血性脑卒中的临床诊疗对提高患者生存率、康复机会和生活质量至关重要。这项工作将帮助医疗界更好地理解如何应对这一重大神经系统疾病，改善患者护理和治疗，推动医学进步，提供更出色的医疗服务。

参考文献