一类斐波那契相似立方体及其计数性质

A Class of Fibonacci Similar Cubes and Their Counting Properties

摘要: L-si-Fibonaccene是一个基于Fibonaccene简单变形得到的六角系统，在其内对偶图上建立了一种特殊偏序，命名为L-栅栏。根据偏序L-栅栏的所有滤子按照反包含关系形成的滤子格，得到了一类新的匹配型分配格，忽略掉其Hasse图中的方向后就得到一个结构和性质都与斐波那契立方体相似的新立方体，并计算了它的秩生成函数、立方体多项式和极大立方体多项式.本文的研究不但为匹配型分配格增加了一类新成员，而且其导出的立方体还可以作为新的内联网的模型。

Abstract: L-si-Fibonaccene is a hexagonal system based on the simple deformation of Fibonaccene, and a special partial order is established on its dual graph, which is named L-fence. According to the filter lattice formed by all the filters of the partially ordered L-barrier according to the inverse inclusion relation, a new class of matched distributive lattices is obtained. After ignoring the direction in its Hasse diagram, a new cube with similar structure and properties to the Fibonacci cube is obtained, and its rank generating function, cube polynomial and maximal cube polynomial are calculated. The research in this paper not only adds a new class of members to the matching distributive lattice, but also the derived cube can be used as a new model of the intranet.

1. 引言

1993年，作为内联网模型，Hsu定义了Fibonacci立方体 ${\Gamma }_n$ [1] 。由于该立方体具有类似超立方的良好性质，可以承载许多超立方上的算法 [2] ，进而引发了对其相关图类及其性质的一系列研究。Munarini和Zagaglia Salvi定义了卢卡斯立方体 ${\Lambda }_n$ [3] [4] 。此外，Fibonacci立方体和卢卡斯立方体的秩生成函数 [5] 、立方体多项式 [6] [7] 、最大立方体多项式 [8] 、不相交立方体多项式 [9] [10] 和度序列多项式 [11] 也得到了研究。同时，Klavžar，Munarini等人 [3] [6] [8] [10] [11] [12] 研究了大量与卢卡斯立方体相关的性质，及其无向Hasse-图上的计数性质；Munarini等人 [5] 还研究了其有向Hasse-图上的秩多项式等计数性质。张和平等人 [13] [14] 在平面基本二部图的完美匹配集合上建立了一个有限分配格——匹配型分配格的概念，并研究了其一些基本性质。Klavžar和Žigert Pleteršek [15] 发现了Fibonacci立方体是Fibonaccenes的共振图。Yao和Zhang进一步证明了定向的Fibonacci立方体都是匹配型分配格 [16] [17] ，其Hasse图同构于Fibonaccenes的共振有向图。然而与斐波那契立方体结构和性质相似的匹配型分配格和立方体的研究成果非常少。本文主要通过提出一个新的偏序集，从而得到了一类新的匹配型分配格，忽略掉其Hasse图中的方向后就得到一个结构和性质都与斐波那契立方体相似的新立方体——L-斐波那契相似立方体，并研究了L-斐波那契相似立方体的一些计数性质。

2. 预备知识

如果一个集合P的序关系 ≤ 满足自反性，反对称性和传递性，那这个集合称为偏序集。设Q是偏序集P的一个子集，则Q也满足P中的偏序关系：任给 $x,y\in Q$ ，若在Q中 $x\le y$ 当且仅当在P中 $x\le y$ 。 $x\prec y$ 表示x被y覆盖或y覆盖x，如果 $x<y$ 且x与y之间再无其它元素 [18] 。设K(可能为空)为偏序集P的一个子集，若 $a,b\in K$ ， $x\in P$ 且 $a\le x\le b$ 时，有 $x\in K$ ，则称K为凸的 [19] 。设集合Q是偏序集P的一个子集，若 $y\in Q$ 且 $y\le z$ 则 $z\in Q$ ，那么Q称为P的一个滤子 [18] ， $\mathcal{F}\left(P\right)$ 表示一个偏序集P的所有滤子。所有滤子 $\mathcal{F}\left(P\right)$ 按照反包含关系( $Y^{\prime }\le Y$ 当且仅当 $Y^{\prime }\supseteq Y$ )构成的偏序集是个分配格，称为滤子格，而且 $\mathcal{F}\left(P\right):=\left(\mathcal{F}\left(P\right),\supseteq \right)$ 是一个有限分配格。在有限分配格 $\mathcal{F}\left(P\right)$ 中， $\hat{1}$ (或 $\hat{0}$ )表示最大(或最小)元 [19] 。若分配格仅含有一个元素，则称分配格是平凡的。设L是一个有限分配格，如果存在一个平面弱基本二部图G使得 $L\cong M\left(G\right)$ ，则称L为匹配型分配格，其中 $M\left(G\right)$ 是在图G的所有完美匹配上建立的有限分配格 [13] 。

设L是一个有限分配格，K是L的一个凸子格(即区间)，若L的任意极大链至少包含K的一个元素，则称K为L的一个割。L关于K的凸扩张 $L⊞K$ 是集合 $L\cup K^{\prime }$ ( $K^{\prime }\cong K$ 是K的拷贝)上的一个分配格( [20] )，其导出关系为：

$x\le y$ ，在L中，若 $x\le y$ ，

$x^{\prime }<y$ ，在L中，若 $x\le y$ 且 $x\in K$ ，

$x<y^{\prime }$ ，在L中，若 $x<y$ 且 $y\in K$ ，

$x^{\prime }\le y^{\prime }$ ，在K中，若 $x\le y$ 。

本文中用到但没解释的概念见文献 [18] [19] 。

一个六角系统是一个没有割点的有限连通平面图，它的每个内面都被边长为1的正六边形包围 [21] 。Fibonaccenes或“Zigzag”六角形链在六角系统中被广泛研究。斐波那契立方体是“Zigzag”六角形链的Z-变换图或共振图 [15] 。我们将“Zigzag”六角形链简单修改得到了一种新的六角系统，并从其内对偶图上得到了一个偏序集，该偏序集的滤子格同构于该六角系统的匹配型分配格(其Hasse图同构于共振有向图 [13] )。

定义2.1 “L-si-Fibonaccene”是在Fibonaccene的左端第二个六角形下面连接了一个额外六角形的Cata型六角系统，如下图1所示。本文中我们将有 $n\left(\ge 3\right)$ 个六角形的L-si-Fibonaccene记为 $Y_n$ 。

Figure 1. L-si-Fibonaccene and its inner dual graph

图1. L-si-Fibonaccene及其内对偶图

Figure 2. Poset ${\psi }_n$

图2. 偏序集 ${\psi }_n$

定义2.2 设 $n\ge 3$ ，称在 $Y_n$ 的内对偶图上的如图2所示的偏序集为L-栅栏，它是由“栅栏”(即“Zigzag”偏序)添加一个极大元得到的，记为 ${\psi }_n$ 。

定理2.3 [14] 设 $n\ge 3$ ， $M\left(Y_n\right)\cong \mathcal{F}\left({\psi }_n\right)$ 是L-si-Fibonaccene $Y_n$ 的匹配型分配格，其Hasse图同构于 $Y_n$ 的有向Z-变换图。

定义2.4 将L-栅栏的滤子格 $\mathcal{F}\left({\psi }_n\right)$ 称为L-斐波那契相似立方体，记为 ${\Psi }_n$ ，为方便计， ${\Psi }_n$ 同时也表示 $\mathcal{F}\left({\psi }_n\right)$ 的Hasse图。

前七个L-斐波那契相似立方体 ${\Psi }_0$ ， ${\Psi }_1$ ， ${\Psi }_2$ ， ${\Psi }_3$ ， ${\Psi }_4$ ， ${\Psi }_5$ ， ${\Psi }_6$ ，如图3所示(其中 ${\Psi }_0$ 表示只有一个顶点的平凡格或图)。

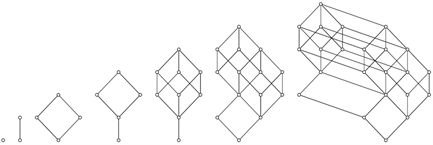
Figure 3. L-Fibonacci similar cube ${\Psi }_0$ , $\cdots$ , ${\Psi }_6$

图3. L-斐波那契相似立方体 ${\Psi }_0$ ， $\cdots$ ， ${\Psi }_6$

引理2.5 [20] 滤子格 $\mathcal{F}\left(P\right)$ 是可以由分配格的凸扩张得到，对任意的 $x\in P$ 有，

$\mathcal{F}\left(P\right)\cong \mathcal{F}\left(P-x\right)⊞\mathcal{F}\left(P\ast x\right)$ ，

其中 $P-x$ 和 $P\ast x$ 分别表示 $P\backslash \left\{x\right\}$ 和 $P\backslash \left\{y\in P|y\le x或x\le y\right\}$ 上的子偏序集。

定理2.6 当 $n\ge 5$ 时有，

${\Psi }_n\cong {\Psi }_{n-1}⊞{\Psi }_{n-2}\cong \left({\Psi }_{n-2}⊞{\Psi }_{n-3}\right)⊞{\Psi }_{n-2}$ .

证明 在 ${\Psi }_n$ 和 ${\Psi }_{n-1}$ 中，分别令 $x=x_n$ 和 $x=x_{n-1}$ ，则根据引理2.5得

$\begin{array}{c}{\Psi }_n=\mathcal{F}\left({\psi }_n\right)=\mathcal{F}\left({\psi }_n-x_n\right)⊞\mathcal{F}\left({\psi }_n\ast x_n\right)\\ =\mathcal{F}\left({\psi }_{n-1}\right)⊞\mathcal{F}\left({\psi }_{n-2}\right)\\ =\left(\mathcal{F}\left({\psi }_{n-1}-x_{n-1}\right)⊞\mathcal{F}\left({\psi }_{n-1}\ast x_{n-1}\right)\right)⊞\mathcal{F}\left({\psi }_{n-2}\right)\\ =\left(\mathcal{F}\left({\psi }_{n-2}\right)⊞\mathcal{F}\left({\psi }_{n-3}\right)\right)⊞\mathcal{F}\left({\psi }_{n-2}\right).\end{array}$

定理2.6得证。

注释2.7 根据上述定理的证明和n的奇偶性，我们得到 ${\Psi }_n$ 的递归结构。当n为偶数时， ${\Psi }_n$ 的所有滤子分为以下三类：不含 $x_{n-1}$ ， $x_n$ 的滤子(因而是 ${\Psi }_{n-2}$ 的滤子，故其导出子格同构于 ${\Psi }_{n-2}$ )；含 $x_n$ 但不含 $x_{n-1}$ 的滤子(因为 $x_n$ 是个极大元，所以删除 $x_n$ 之后是 ${\Psi }_{n-2}$ 的滤子，反之亦然，故其导出子格同构于 ${\Psi }_{n-2}$ )；同时包含 $x_{n-1}$ 和 $x_n$ 的滤子(因为 $x_n$ 是个极大元， $x_{n-1}$ 是个极小元，所以删除 $x_{n-1}$ (同时必须删去 $x_n$ 和 $x_{n-2}$ )之后是 ${\Psi }_{n-3}$ 的滤子，反之亦然，故其导出子格同构于 ${\Psi }_{n-3}$ )。由反包含关系可以得知第一类中的滤子大于第二类中对应的滤子，第二类中的滤子大于第三类中对应的滤子(如图4(a)所示)。当n为奇数时， ${\Psi }_n$ 的所有滤子分为以下三类：不含 $x_{n-2}$ ， $x_{n-1}$ ， $x_n$ 的滤子(因而是 ${\Psi }_{n-3}$ 的所有滤子，故其导出子格同构于 ${\Psi }_{n-3}$ )；含 $x_{n-1}$ 但不含 $x_n$ 的滤子(因为 $x_{n-1}$ 是个极大元，所以删除 $x_{n-1}$ 之后是 ${\Psi }_{n-2}$ 的所有滤子，反之亦然，故其导出子格同构于 ${\Psi }_{n-2}$ )；同时包含 $x_{n-1}$ 和 $x_n$ 的滤子(因为 $x_{n-1}$ 是个极大元， $x_n$ 是个极小元，所以删除 $x_n$ 和 $x_{n-1}$ 之后是 ${\Psi }_{n-2}$ 的所有滤子，反之亦然，故其导出子格同构于 ${\Psi }_{n-2}$ )。由反包含关系可以得知第一类中的滤子大于第二类中对应的滤子，第二类中的滤子大于第三类中对应的滤子(如图4(b)所示)。

3. 计数性质

3.1. 秩生成函数

设 ${\Psi }_n$ 的秩生成函数为 $R_n^L\left(x\right):=R\left({\Psi }_n,x\right)={\displaystyle \underset{k\ge 0}{\sum }{r}_{n,k}^L}{x}^k$ ，其中 $r_{n,k}^L:=r_k\left({\Psi }_n\right)$ 表示 ${\Psi }_n$ 中秩为k的元素的数目。其中部分 ${\Psi }_n$ 的秩生成函数如下：

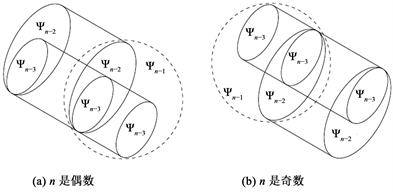
Figure 4. The recursive structure diagram of ${\Psi }_n$

图4. ${\Psi }_n$ 的递归结构图

$\begin{array}{c}{R}_0^L\left(x\right)=1,\\ R_1^L\left(x\right)=1+x,\\ R_2^L\left(x\right)=1+2x+x^2,\\ R_3^L\left(x\right)=1+x+2x^2+x^3,\end{array}$

$\begin{array}{c}{R}_4^L\left(x\right)=1+x+3x^2+3x^3+x^4,\\ R_5^L\left(x\right)=1+2x+3x^2+4x^3+3x^4+x^5,\\ R_6^L\left(x\right)=1+2x+4x^2+5x^3+6x^4+4x^5+x^6,\\ R_7^L\left(x\right)=1+3x+5x^2+8x^3+8x^4+7x^5+4x^6+x^7.\end{array}$

引理3.1 [20] 设L是一个有限分配格且K是L的一个割，则 $L⊞K$ 的秩生成函数为

$R\left(L⊞K,x\right)=\{\begin{array}{l}R\left(L,x\right)+x^{h_L\left({\hat{0}}_K\right)+1}R\left(K,x\right),\text{if}{\hat{1}}_K={\hat{1}}_L;\\ R\left(K,x\right)+xR\left(L,x\right),\text{if}{\hat{0}}_K={\hat{0}}_L.\end{array}$

其中 $h_L\left(x\right)$ 表示L中任意元素x的高。

由引理3.1我们有如下命题。

命题3.2 当 $n\ge 4$ 时，

$R_n^L\left(x\right)=\{\begin{array}{l}x{R}_{n-1}^L\left(x\right)+R_{n-2}^L\left(x\right),n为奇数,\\ R_{n-1}^L\left(x\right)+x^2{R}_{n-2}^L\left(x\right),n为偶数.\end{array}$

换句话说，当 $m\ge 2$ 时，

$\{\begin{array}{l}{R}_{2m+1}^L\left(x\right)=x{R}_{2m}^L\left(x\right)+R_{2m-1}^L\left(x\right),\\ R_{2m}^L\left(x\right)=R_{2m-1}^L\left(x\right)+x^2{R}_{2m-2}^L\left(x\right).\end{array}$

设 $A_m\left(x\right)=R_{2m}^L\left(x\right)$ ， $B_m\left(x\right)=R_{2m+1}^L\left(x\right)$ ，当 $m\ge 2$ 时，我们有

$\{\begin{array}{l}{A}_m\left(x\right)=B_{m-1}\left(x\right)+x^2{A}_{m-1}\left(x\right),\\ B_m\left(x\right)=x{A}_m\left(x\right)+B_{m-1}\left(x\right).\end{array}$

我们有 $A_m\left(x\right)$ 和 $B_m\left(x\right)$ 的递推关系。

命题3.3 设 $A_m\left(x\right)=R_{2m}^L\left(x\right)$ ， $B_m\left(x\right)=R_{2m+1}^L\left(x\right)$ ，

$\{\begin{array}{l}{A}_m\left(x\right)=\left(1+x+x^2\right)A_{m-1}\left(x\right)-x^2{A}_{m-2}\left(x\right),\left(m\ge 3\right),\\ B_m\left(x\right)=\left(1+x+x^2\right)B_{m-1}\left(x\right)-x^2{B}_{m-2}\left(x\right),\left(m\ge 3\right).\end{array}$

证明 由上述得，当 $m\ge 3$ 时，

$\begin{array}{c}{A}_m\left(x\right)=B_{m-1}\left(x\right)+x^2{A}_{m-1}\left(x\right)\\ =x{A}_{m-1}\left(x\right)+B_{m-2}\left(x\right)+x^2{A}_{m-1}\left(x\right)\\ =x{A}_{m-1}\left(x\right)+A_{m-1}\left(x\right)-x^2{A}_{m-2}\left(x\right)+x^2{A}_{m-1}\left(x\right)\\ =\left(1+x+x^2\right)A_{m-1}\left(x\right)-x^2{A}_{m-2}(\; x\; )\end{array}$

相似地，我们可得到 $B_m\left(x\right)$ 的递推关系。

由命题3.3可得 $A_m\left(x\right)$ 和 $B_m\left(x\right)$ 的生成函数，也可通过当 $n\ge 10$ 时，

$\begin{array}{c}P\left({\Psi }_n\right)=\left(2xy+x+y\right)P\left({\Psi }_{n-2}\right)-xy\left(xy+2x+2y-1\right)P\left({\Psi }_{n-4}\right)\\ +xy\left(x^{2}y+x{y}^2-x-y+1\right)P\left({\Psi }_{n-6}\right)-x^2{y}^2\left(1-x\right)\left(1-y\right)P\left({\Psi }_{n-8}\right),\end{array}$

直接得到。

定理3.4 $A_m\left(x\right)$ 和 $B_m\left(x\right)$ 的生成函数为

${\displaystyle \underset{m\ge 0}{\sum }{A}_m}\left(x\right)z^m=\frac{1+xz-2x{z}^2}{1-\left(1+x+x^2\right)z+x^2{z}^2}$

且

${\displaystyle \underset{m\ge 0}{\sum }{B}_m}\left(x\right)z^m=\frac{1+x-xz+x^3{z}^2}{1-\left(1+x+x^2\right)z+x^2{z}^2}.$

证明 由命题3.3得，

$\begin{array}{c}{\displaystyle \underset{m\ge 0}{\sum }{A}_m}\left(x\right)z^m={\displaystyle \underset{m\ge 3}{\sum }{A}_m}\left(x\right)z^m+A_2\left(x\right)z^2+A_1\left(x\right)z+A_0\left(x\right)\\ ={\displaystyle \underset{m\ge 3}{\sum }\left(\left(1+x+x^2\right)A_{m-1}-x^2{A}_{m-2}\right)z^m}+A_2{z}^2+A_{1}z+A_0\\ =\left(1+x+x^2\right)z{\displaystyle \underset{m\ge 2}{\sum }{A}_m}\left(x\right)z^m-x^2{z}^2{\displaystyle \underset{m\ge 1}{\sum }{A}_m}\left(x\right)z^m+A_2\left(x\right)z^2+A_1\left(x\right)z+A_0\left(x\right)\\ =\left(1+x+x^2\right)z{\displaystyle \underset{m\ge 0}{\sum }{A}_m}\left(x\right)z^m-x^2{z}^2{\displaystyle \underset{m\ge 0}{\sum }{A}_m}\left(x\right)z^m+1+xz-2x{z}^2\end{array}$

同理可得 $B_m\left(x\right)$ 的生成函数。

证明完毕。

设 $\left(\begin{array}{c}n;3\\ k\end{array}\right)$ [22] 表示 ${\left(1+x+x^2\right)}^n$ 中 $x^k$ 的系数，并且有

$\left(\begin{array}{c}n;3\\ k\end{array}\right)={\displaystyle \underset{i=0}{\overset{\lfloor \frac{k}{2}\rfloor }{\sum }}\left(\begin{array}{c}n\\ k-i\end{array}\right)}\left(\begin{array}{c}k-i\\ i\end{array}\right),$

在OEIS [23] 中参考数列A027907。

定理3.5

$\begin{array}{c}{r}_{2m,k}^L={\displaystyle \underset{i=0}{\overset{\lfloor \frac{m}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i\\ i\end{array}\right)\left(\begin{array}{c}m-2i;3\\ k-2i\end{array}\right)+{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-1}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-1\\ i\end{array}\right)\left(\begin{array}{c}m-2i-1;3\\ k-2i-1\end{array}\right)\\ -2{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-2}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-2\\ i\end{array}\right)\left(\begin{array}{c}m-2i-2;3\\ k-2i-1\end{array}\right).\end{array}$

且

$\begin{array}{c}{r}_{2m+1,k}^L={\displaystyle \underset{i=0}{\overset{\lfloor \frac{m}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i\\ i\end{array}\right)\left(\left(\begin{array}{c}m-2i;3\\ k-2i\end{array}\right)+\left(\begin{array}{c}m-2i;3\\ k-2i-1\end{array}\right)\right)\\ -{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-1}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-1\\ i\end{array}\right)\left(\begin{array}{c}m-2i-1;3\\ k-2i-1\end{array}\right)+{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-2}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-2\\ i\end{array}\right)\left(\begin{array}{c}m-2i-2;3\\ k-2i-3\end{array}\right).\end{array}$

证明 其中多项式 $\left\{g_n\left(x\right)\right\}$ 可如下定义

${\displaystyle \underset{n\ge 0}{\sum }{g}_n}\left(x\right)z^n=\frac{1}{1-\left(1+x+x^2\right)z+x^2{z}^2}$

所以有

$g_n\left(x\right)={\displaystyle \underset{i=0}{\overset{\lfloor \frac{n}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}n-i\\ i\end{array}\right)x^{2i}{\left(1+x+x^2\right)}^{n-2i}.$

此外， $g_n\left(x\right)$ 中 $x^k$ 的系数可如下得到

$\left[x^k\right]g_n\left(x\right)={\displaystyle \underset{i=0}{\overset{\lfloor \frac{n}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}n-i\\ i\end{array}\right)x^{2i}{\left(1+x+x^2\right)}^{n-2i}={\displaystyle \underset{i=0}{\overset{\lfloor \frac{n}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}n-i\\ i\end{array}\right)\left(\begin{array}{c}n-2i;3\\ k-2i\end{array}\right).$

所以，由 $A_m\left(x\right)=g_m\left(x\right)+x{g}_{m-1}\left(x\right)-2x{g}_{m-2}\left(x\right)$ ，我们有

$\begin{array}{c}{r}_{2m,k}^L=\left[x^k\right]A_m\left(x\right)=\left[x^k\right]g_m\left(x\right)+\left[x^{k-1}\right]g_{m-1}\left(x\right)-2\left[x^{k-1}\right]g_{m-2}\left(x\right)\\ ={\displaystyle \underset{i=0}{\overset{\lfloor \frac{m}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i\\ i\end{array}\right)\left(\begin{array}{c}m-2i;3\\ k-2i\end{array}\right)+{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-1}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-1\\ i\end{array}\right)\left(\begin{array}{c}m-2i-1;3\\ k-2i-1\end{array}\right)\\ -2{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-2}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-2\\ i\end{array}\right)\left(\begin{array}{c}m-2i-2;3\\ k-2i-1\end{array}\right).\end{array}$

同理， $r_{2m+1,k}^L$ 可由 $B_m\left(x\right)=g_m\left(x\right)+x{g}_m\left(x\right)-x{g}_{m-1}\left(x\right)+x^3{g}_{m-2}\left(x\right)$ 得到。

$\begin{array}{c}{r}_{2m+1,k}^L=\left[x^k\right]A_m\left(x\right)=\left[x^k\right]g_m\left(x\right)+\left[x^{k-1}\right]g_{m-1}\left(x\right)-2\left[x^{k-1}\right]g_{m-2}\left(x\right)\\ ={\displaystyle \underset{i=0}{\overset{\lfloor \frac{m}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i\\ i\end{array}\right)\left(\left(\begin{array}{c}m-2i;3\\ k-2i\end{array}\right)+\left(\begin{array}{c}m-2i;3\\ k-2i-1\end{array}\right)\right)\\ -{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-1}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-1\\ i\end{array}\right)\left(\begin{array}{c}m-2i-1;3\\ k-2i-1\end{array}\right)+{\displaystyle \underset{i=0}{\overset{\lfloor \frac{m-2}{2}\rfloor }{\sum }}{\left(-1\right)}^i}\left(\begin{array}{c}m-i-2\\ i\end{array}\right)\left(\begin{array}{c}m-2i-2;3\\ k-2i-3\end{array}\right)\end{array}$

证毕。

由定理3.4我们可得到关于 $R_n^L\left(x\right)$ 的生成函数的结论。

定理3.6 $R_n^L\left(x\right)$ 的生成函数为

${\displaystyle \underset{n\ge 0}{\sum }{R}_n^L}\left(x\right)y^n=\frac{1+\left(1+x\right)y+x{y}^2-x{y}^3-2x{y}^4+x^3{y}^5}{1-\left(1+x+x^2\right)y^2+x^2{y}^4}.$

证明 由 $A_m\left(x\right)$ 和 $B_m\left(x\right)$ 的定义，

$\begin{array}{c}{\displaystyle \underset{n\ge 0}{\sum }{R}_n^L}\left(x\right)y^n={\displaystyle \underset{m\ge 0}{\sum }{A}_m}\left(x\right)y^{2m}+{\displaystyle \underset{m\ge 0}{\sum }{B}_m}\left(x\right)y^{2m+1}\\ ={\displaystyle \underset{m\ge 0}{\sum }{A}_m}\left(x\right)y^{2m}+y{\displaystyle \underset{m\ge 0}{\sum }{B}_m}\left(x\right)y^{2m}\\ =\frac{1+x{y}^2-2x{y}^4}{1-\left(1+x+x^2\right)y^2+x^2{y}^4}+y\frac{1+x-x{y}^2+x^3{y}^4}{1-\left(1+x+x^2\right)y^2+x^2{y}^4}\\ =\frac{1+\left(1+x\right)y+x{y}^2-x{y}^3-2x{y}^4+x^3{y}^5}{1-\left(1+x+x^2\right)y^2+x^2{y}^4}\end{array}$

证毕。

在秩生成函数中取 $x=1$ 我们有 ${\Psi }_n$ 的顶点生成函数为

推论3.7

${\displaystyle \underset{n\ge 0}{\sum }{R}_n^L}\left(1\right)y^n=\frac{1+y+y^2-y^3}{1-y-y^2}=-2+y+\frac{3-2y}{1-y-y^2}$

因此有顶点的递推关系为

$\{\begin{array}{l}{R}_n^L\left(1\right)=R_{n-1}^L\left(1\right)+R_{n-2}^L\left(1\right)\left(n\ge 4\right),\\ R_2^L\left(1\right)=4,R_3^L\left(1\right)=5.\end{array}$

顶点序列中去掉 $R_0^L\left(1\right)=1$ ， $R_1^L\left(1\right)=2$ 得到OEIS中的类斐波那契数列A104449 (去掉前两项：(3, 1) 4, 5, 9, 14, 23, 37, 60, 97...)。

3.2. 立方体多项式

设 ${\Psi }_n$ 的立方体多项式为 $Q_n^L\left(x\right)={\displaystyle \underset{k\ge 0}{\sum }{q}_{n,k}^L}{x}^k$ ，其中 $q_{n,k}^L:=q_k\left({\Psi }_n\right)$ 表示 ${\Psi }_n$ 中k维立方体的个数。其中部分立方体多项式 $Q_n^L\left(x\right)$ 如下：

$\begin{array}{l}{Q}_0^L\left(x\right)=1\\ Q_1^L\left(x\right)=2+x\\ Q_2^L\left(x\right)=4+4x+x^2\\ Q_3^L\left(x\right)=5+5x+x^2\\ Q_4^L\left(x\right)=9+13x+6x^2+x^3\\ Q_5^L\left(x\right)=14+23x+12x^2+2x^3\\ Q_6^L\left(x\right)=23+45x+31x^2+9x^3+x^4\end{array}$

引理3.8. [20] 设L是一个有限分配格且K是L的一个割。则

$q_k\left(L⊞K\right)=q_k\left(L\right)+q_k\left(K\right)+q_{k-1}\left(K\right).$

由引理3.8我们可得 $q_{n,k}$ 的递推关系。

命题3.9 当 $n\ge 4$ 时，

$q_{n,k}^L=q_{n-1,k}^L+q_{n-2,k}^L+q_{n-2,k-1}^L.$

由此易得 $Q_n\left(x\right)$ 的递推关系。

命题3.10 当 $n\ge 4$ 时，

$Q_n^L\left(x\right)=Q_{n-1}^L\left(x\right)+\left(1+x\right)Q_{n-2}^L\left(x\right).$

证明 由命题3.9可得，

$\begin{array}{c}{Q}_n^L\left(x\right)={\displaystyle \underset{k\ge 0}{\sum }{q}_{n,k}^L}{x}^k={\displaystyle \underset{k\ge 0}{\sum }\left(q_{n-1,k}^L+q_{n-2,k}^L+q_{n-2,k-1}^L\right)x^k}\\ ={\displaystyle \underset{k\ge 0}{\sum }{q}_{n-1,k}^L}{x}^k+{\displaystyle \underset{k\ge 0}{\sum }{q}_{n-2,k}^L}{x}^k+x{\displaystyle \underset{k\ge 0}{\sum }{q}_{n-2,k-1}^L}{x}^{k-1}\\ =Q_{n-1}^L\left(x\right)+\left(1+x\right)Q_{n-2}^L(\; x\; )\end{array}$

证毕。

定理3.11 $Q_n^L\left(x\right)$ 的生成函数为

${\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n=\frac{y^2{\left(1+x\right)}^2+1+\left(1+x\right)y-y^3{\left(1+x\right)}^2}{1-y-y^2-x{y}^2}.$

证明

$\begin{array}{c}{\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n={\displaystyle \underset{n\ge 4}{\sum }{Q}_n^L}\left(x\right)y^n+{\displaystyle \underset{n=0}{\overset{3}{\sum }}{Q}_n^L}\left(x\right)y^n\\ ={\displaystyle \underset{n\ge 4}{\sum }\left(Q_{n-1}^L\left(x\right)+\left(1+x\right)Q_{n-2}^L\left(x\right)\right)y^n}+Q_3^L\left(x\right)y^3+Q_2^L\left(x\right)y^2+Q_1^L\left(x\right)y+Q_0^L\left(x\right)\\ ={\displaystyle \underset{n\ge 4}{\sum }{Q}_{n-1}^L}\left(x\right)y^n+{\displaystyle \underset{n\ge 4}{\sum }{Q}_{n-2}^L}\left(x\right)y^n+{\displaystyle \underset{n-2}{\sum }x}{Q}_{n-2}^L\left(x\right)+Q_3^L\left(x\right)y^3+Q_2^L\left(x\right)y^2\\ +Q_1^L\left(x\right)y+Q_0^L(\; x\; )\end{array}$

$\begin{array}{c}=y\left({\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n-Q_2^L\left(x\right)y^2-Q_1^L\left(x\right)y-Q_0^L\left(x\right)\right)+y^2{\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n-Q_1^L\left(x\right)y^3\\ -Q_0^L\left(x\right)y^2+x{y}^2\left({\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n-Q_1^L\left(x\right)y-Q_0^L\left(x\right)\right)\\ +Q_2^L\left(x\right)y^2+Q_1^L\left(x\right)y+Q_0^L\left(x\right)\\ =\left(y+y^2+x{y}^2\right){\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n+y^2{\left(1+x\right)}^2+1+\left(1+x\right)y-y^3{\left(1+x\right)}^2\end{array}$

证毕。

立方体多项式可从 $Q_n^L\left(x\right)$ 的生成函数中导出。

推论3.12 当 $n\ge 3$ 时，

$\begin{array}{c}{Q}_n^L\left(x\right)={\displaystyle \underset{j=\lfloor \frac{n-1}{2}\rfloor }{\overset{n}{\sum }}\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}{\left(1+x\right)}^{n-j}+{\displaystyle \underset{j=\lfloor \frac{n-2}{2}\rfloor }{\overset{n-2}{\sum }}\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}{\left(1+x\right)}^{n-j}\\ -{\displaystyle \underset{j=\lfloor \frac{n-3}{2}\rfloor }{\overset{n-3}{\sum }}\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}{\left(1+x\right)}^{n-j-1}\end{array}$

并且有

$\begin{array}{c}{q}_{n,k}^L={\displaystyle \underset{j=\lfloor \frac{n}{2}\rfloor }{\overset{n}{\sum }}\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}\left(\begin{array}{c}n-j\\ k\end{array}\right)+{\displaystyle \underset{j=\lfloor \frac{n-2}{2}\rfloor }{\overset{n-2}{\sum }}\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}\left(\begin{array}{c}n-j\\ k\end{array}\right)\\ -{\displaystyle \underset{j=\lfloor \frac{n-3}{2}\rfloor }{\overset{n-3}{\sum }}\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}\left(\begin{array}{c}n-j-1\\ k\end{array}\right).\end{array}$

证明

$\begin{array}{c}{\displaystyle \underset{n\ge 0}{\sum }{Q}_n^L}\left(x\right)y^n=\frac{1+\left(1+x\right)y+y^2{\left(1+x\right)}^2-y^3{\left(1+x\right)}^2}{1-y-\left(1+x\right)y^2}\\ =\left(1+\left(1+x\right)y+y^2{\left(1+x\right)}^2-y^3{\left(1+x\right)}^2\right){\displaystyle \underset{j\ge 0}{\sum }{\left(y+\left(1+x\right)y^2\right)}^j}\\ ={\displaystyle \underset{j\ge 0}{\sum }{y}^j}{\left(1+\left(1+x\right)y\right)}^{j+1}+y^2{\left(1+x\right)}^2{\displaystyle \underset{j\ge 0}{\sum }{y}^j}{\left(1+\left(1+x\right)y\right)}^j\\ -y^3{\left(1+x\right)}^2{\displaystyle \underset{j\ge 0}{\sum }{y}^j}{\left(1+\left(1+x\right)y\right)}^j\end{array}$

$\begin{array}{c}={\displaystyle \underset{j\ge 0}{\sum }{\displaystyle \underset{n-j\ge 0}{\sum }\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}}{\left(1+x\right)}^{n-j}{y}^n+{\left(1+x\right)}^2{\displaystyle \underset{j\ge 0}{\sum }{\displaystyle \underset{n-j-2\ge 0}{\sum }\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}}{\left(1+x\right)}^{n-j-2}{y}^n\\ -{\left(1+x\right)}^2{\displaystyle \underset{j\ge 0}{\sum }{\displaystyle \underset{n-j-3\ge 0}{\sum }\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}}{\left(1+x\right)}^{n-j-3}{y}^n\\ ={\displaystyle \underset{n\ge 0}{\sum }{\displaystyle \underset{j=\lfloor \frac{n}{2}\rfloor }{\overset{n}{\sum }}\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}}{\left(1+x\right)}^{n-j}{y}^n+{\displaystyle \underset{n\ge 0}{\sum }{\displaystyle \underset{j=\lfloor \frac{n-2}{2}\rfloor }{\overset{n-2}{\sum }}\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}}{\left(1+x\right)}^{n-j}{y}^n\\ -{\displaystyle \underset{n\ge 0}{\sum }{\displaystyle \underset{j=\lfloor \frac{n-3}{2}\rfloor }{\overset{n-3}{\sum }}\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}}{\left(1+x\right)}^{n-j-1}{y}^n\end{array}$

所以，

$\begin{array}{c}{Q}_n^L\left(x\right)={\displaystyle \underset{j=\lfloor \frac{n}{2}\rfloor }{\overset{n}{\sum }}\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}{\left(1+x\right)}^{n-j}+{\displaystyle \underset{j=\lfloor \frac{n-2}{2}\rfloor }{\overset{n-2}{\sum }}\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}{\left(1+x\right)}^{n-j}-{\displaystyle \underset{j=\lfloor \frac{n-3}{2}\rfloor }{\overset{n-3}{\sum }}\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}{\left(1+x\right)}^{n-j-1}\\ ={\displaystyle \underset{j=\lfloor \frac{n}{2}\rfloor }{\overset{n}{\sum }}{\displaystyle \underset{k=0}{\overset{n-j}{\sum }}\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}}\left(\begin{array}{c}n-j\\ k\end{array}\right)x^k+{\displaystyle \underset{\lfloor \frac{n-2}{2}\rfloor }{\overset{n-2}{\sum }}{\displaystyle \underset{k=0}{\overset{n-j}{\sum }}\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}}\left(\begin{array}{c}n-j\\ k\end{array}\right)x^k\\ -{\displaystyle \underset{j=\lfloor \frac{n-3}{2}\rfloor }{\overset{n-3}{\sum }}{\displaystyle \underset{k=0}{\overset{n-j-1}{\sum }}\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}}\left(\begin{array}{c}n-j-1\\ k\end{array}\right)x^k\\ ={\displaystyle \underset{k\ge 0}{\sum }{\displaystyle \underset{j=\lfloor \frac{n}{2}\rfloor }{\overset{n}{\sum }}\left(\begin{array}{c}j+1\\ n-j\end{array}\right)}}\left(\begin{array}{c}n-j\\ k\end{array}\right)x^k+{\displaystyle \underset{k\ge 0}{\sum }{\displaystyle \underset{j=\lfloor \frac{n-2}{2}\rfloor }{\overset{n-2}{\sum }}\left(\begin{array}{c}j\\ n-j-2\end{array}\right)}}\left(\begin{array}{c}n-j\\ k\end{array}\right)x^k\\ -{\displaystyle \underset{k\ge 0}{\sum }{\displaystyle \underset{j=\lfloor \frac{n-3}{2}\rfloor }{\overset{n-3}{\sum }}\left(\begin{array}{c}j\\ n-j-3\end{array}\right)}}\left(\begin{array}{c}n-j-1\\ k\end{array}\right)x^k.\end{array}$

因此，可得 $Q_n^L\left(x\right)$ 。

3.3. 极大立方体多项式

极大立方体是指不包含在其他更高维立方体中的立方体。设的极大立方体多项式为 $H_n^L\left(x\right)={\displaystyle \underset{k\ge 0}{\sum }{h}_{n,k}^L}{x}^k$ ，其中 $h_{n,k}^L:=h_k\left({\Psi }_n\right)$ 表示 ${\Psi }_n$ 中极大k维立方体的数目，其部分极大立方体多项式 $H_n^L\left(x\right)$ 如下：

$\begin{array}{l}{H}_0^L\left(x\right)=1\\ H_1^L\left(x\right)=x\\ H_2^L\left(x\right)=x^2\\ H_3^L\left(x\right)=x+x^2\\ H_4^L\left(x\right)=x+x^3\\ H_5^L\left(x\right)=x^2+2x^3\\ H_6^L\left(x\right)=2x^2+x^3+x^4\\ H_7^L\left(x\right)=x^2+x^3+3x^4\\ H_8^L\left(x\right)=3x^3+3x^4+x^5\end{array}$

由定理2.6和注释2.7可得 $h_{n,k}^L$ 的递推关系。

命题3.13 当 $n\ge 4$ 时，

$h_{n,k}^L=h_{n-2,k-1}^L+h_{n-3,k-1}^L.$

由命题3.13易得 $H_n^L\left(x\right)$ 递推关系。

命题3.14 当 $n\ge 5$ 时，

$H_n^L\left(x\right)=x{H}_{n-2}^L\left(x\right)+x{H}_{n-3}^L\left(x\right).$

推论3.15 当 $n\ge 4$ 时，我们有

$H_n^L\left(1\right)=H_{n-2}^L\left(1\right)+H_{n-3}^L\left(1\right).$

$\left(1,0,0\right)$ -Padovan数列 $a\left(n\right)$ 定义为： $a\left(0\right)=1$ ， $a\left(1\right)=a\left(2\right)=0$ ， $a\left(n\right)=a\left(n-2\right)+a\left(n-3\right)$ ，其中 $n\ge 0$ (在OEIS [23] }中参考数列A000931)。因此我们有如下推论。

推论3.16 当 $n\ge 0$ 时，

$H_n^L\left(1\right)=a\left(n+5\right).$

此外，由命题3.14我们可得 $H_n^L\left(x\right)$ 的生成函数。

定理3.17 $H_n^L\left(x\right)$ 的生成函数为

${\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{H}_n^L\left(x\right)y^n}=\frac{1+xy+x^2{y}^2+x{y}^4-x{y}^2-x^2{y}^4}{1-\left(x{y}^2+x{y}^3\right)}$

证明 由命题3.14得，

$\begin{array}{c}{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{H}_n^L\left(x\right)y^n}={\displaystyle \underset{n=5}{\overset{\infty }{\sum }}{H}_n^L\left(x\right)y^n}+{\displaystyle \underset{n=0}{\overset{4}{\sum }}{H}_n^L}\left(x\right)y^n\\ ={\displaystyle \underset{n=5}{\overset{\infty }{\sum }}\left(x{H}_{n-2}^L\left(x\right)+x{H}_{n-3}^L\left(x\right)\right)y^n}+{\displaystyle \underset{n=0}{\overset{4}{\sum }}{H}_n^L}\left(x\right)y^n\\ =x{\displaystyle \underset{n=5}{\overset{\infty }{\sum }}{H}_{n-2}^L}\left(x\right)y^n+x{\displaystyle \underset{n=5}{\overset{\infty }{\sum }}{H}_{n-3}^L}\left(x\right)y^n+{\displaystyle \underset{n=0}{\overset{4}{\sum }}{H}_n^L}\left(x\right)y^n\\ =x{y}^2{\displaystyle \underset{n=5}{\overset{\infty }{\sum }}{H}_{n-2}^L}\left(x\right)y^{n-2}+x{y}^3{\displaystyle \underset{n=5}{\overset{\infty }{\sum }}{H}_{n-3}^L}\left(x\right)y^{n-3}+{\displaystyle \underset{n=0}{\overset{4}{\sum }}{H}_n^L}\left(x\right)y^n\\ =x{y}^2{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{H}_n^L}\left(x\right)y^n-x{y}^2{H}_0^L\left(x\right)-x{y}^2{H}_1^L\left(x\right)y-x{y}^2{H}_2^L\left(x\right)y^2\\ +x{y}^3{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{H}_n^L}\left(x\right)y^n-x{y}^3{H}_0^L\left(x\right)-x{y}^3{H}_1^L\left(x\right)y+H_0^L\left(x\right)\\ +H_1^L\left(x\right)y+H_2^L\left(x\right)y^2+H_3^L\left(x\right)y^3+H_4^L\left(x\right)y^4\\ =\left(x{y}^2+x{y}^3\right){\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{H}_n^L}\left(x\right)y^n+1+xy+x^2{y}^2+x{y}^4-x{y}^2-x^2{y}^4.\end{array}$

将 ${\displaystyle \underset{n\ge 0}{\sum }{H}_n^L}\left(x\right)y^n$ 利用二项式展开可得如下结论。

推论3.18 当 $n\ge 4$ 时，

$\begin{array}{c}{H}_n^L\left(x\right)={\displaystyle \underset{k=\lfloor \frac{n}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}k\\ n-2k\end{array}\right)x^k}+{\displaystyle \underset{k=\lfloor \frac{n+2}{3}\rfloor }{\overset{\frac{n+1}{2}}{\sum }}\left(\begin{array}{c}k-1\\ n-2k+1\end{array}\right)x^k}+{\displaystyle \underset{k=\lfloor \frac{n+4}{3}\rfloor }{\overset{\frac{n+2}{2}}{\sum }}\left(\begin{array}{c}k-2\\ n-2k+2\end{array}\right)x^k}\\ +{\displaystyle \underset{k=\lfloor \frac{n-1}{3}\rfloor }{\overset{\frac{n-2}{2}}{\sum }}\left(\begin{array}{c}k-1\\ n-2k-2\end{array}\right)x^k}-{\displaystyle \underset{k=\lfloor \frac{n+1}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}k-1\\ n-2k\end{array}\right)x^k}-{\displaystyle \underset{k=\lfloor \frac{n+2}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}k-2\\ n-2k\end{array}\right)x^k}.\end{array}$

证明 此证明分为两部分进行

${\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{H}_n^L}\left(x\right)y^n=\frac{1+xy+x^2{y}^2+x{y}^4-x{y}^2-x^2{y}^4}{1-x{y}^2\left(1+y\right)}=\frac{1+xy+x^2{y}^2}{1-x{y}^2\left(1+y\right)}+\frac{x{y}^4-x{y}^2-x^2{y}^4}{1-x{y}^2\left(1+y\right)}.$

其中第一部分为

$\begin{array}{l}\frac{1+xy+x^2{y}^2}{1-x{y}^2\left(1+y\right)}\\ =\left(1+xy+x^2{y}^2\right){\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\left(x{y}^2\left(1+y\right)\right)}^j}\\ ={\displaystyle \underset{j\ge 0}{\sum }{x}^j{y}^{2j}{\left(1+y\right)}^j}+{\displaystyle \underset{j\ge 0}{\sum }{x}^{j+1}{y}^{2j+1}{\left(1+y\right)}^j}+{\displaystyle \underset{j\ge 0}{\sum }{x}^{j+2}{y}^{2j+2}{\left(1+y\right)}^j}\\ ={\displaystyle \underset{j\ge 0}{\overset{}{\sum }}{\displaystyle \underset{n-2j=0}{\overset{j}{\sum }}\left(\begin{array}{c}j\\ n-2j\end{array}\right)x^j{y}^n}}+{\displaystyle \underset{j\ge 0}{\overset{}{\sum }}{\displaystyle \underset{n-2j-1=0}{\overset{j}{\sum }}\left(\begin{array}{c}j\\ n-2j-1\end{array}\right)x^{j+1}{y}^n}}+{\displaystyle \underset{j\ge 0}{\overset{}{\sum }}{\displaystyle \underset{n-2j-1=0}{\overset{j}{\sum }}\left(\begin{array}{c}j\\ n-2j-2\end{array}\right)x^{j+2}{y}^n}}\\ ={\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{j=\lfloor \frac{n}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}j\\ n-2j\end{array}\right)x^j{y}^n}}+{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{j=\lfloor \frac{n-1}{3}\rfloor }{\overset{\frac{n-1}{2}}{\sum }}\left(\begin{array}{c}j\\ n-2j-1\end{array}\right)x^{j+1}{y}^n}}+{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{j=\lfloor \frac{n-2}{3}\rfloor }{\overset{\frac{n-2}{2}}{\sum }}\left(\begin{array}{c}j\\ n-2j-2\end{array}\right)x^{j+2}{y}^n}}\\ ={\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{k=\lfloor \frac{n}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}k\\ n-2k\end{array}\right)x^k{y}^n}}+{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{k=\lfloor \frac{n+2}{3}\rfloor }{\overset{\frac{n+1}{2}}{\sum }}\left(\begin{array}{c}k-1\\ n-2k+1\end{array}\right)x^k{y}^n}}+{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{k=\lfloor \frac{n+4}{3}\rfloor }{\overset{\frac{n+2}{2}}{\sum }}\left(\begin{array}{c}k-2\\ n-2k+2\end{array}\right)x^k{y}^n}}.\end{array}$

第二部分为

$\begin{array}{l}\frac{x{y}^4-x{y}^2-x^2{y}^4}{1-x{y}^2\left(1+y\right)}\\ =\left(x{y}^4-x{y}^2-x^2{y}^4\right){\displaystyle \underset{j=0}{\overset{\infty }{\sum }}{\left(x{y}^2\left(1+y\right)\right)}^j}\\ ={\displaystyle \underset{j\ge 0}{\sum }{x}^{j+1}{y}^{2j+4}{\left(1+y\right)}^j}-{\displaystyle \underset{j\ge 0}{\sum }{x}^{j+1}{y}^{2j+2}{\left(1+y\right)}^j}-{\displaystyle \underset{j\ge 0}{\sum }{x}^{j+2}{y}^{2j+4}{\left(1+y\right)}^j}\\ ={\displaystyle \underset{j\ge 0}{\overset{}{\sum }}{\displaystyle \underset{n-2j+4=0}{\overset{j}{\sum }}\left(\begin{array}{c}j\\ n-2j-4\end{array}\right)x^j{y}^n}}-{\displaystyle \underset{j\ge 0}{\overset{}{\sum }}{\displaystyle \underset{n-2j-2=0}{\overset{j}{\sum }}\left(\begin{array}{c}j\\ n-2j-2\end{array}\right)x^{j+1}{y}^n}}-{\displaystyle \underset{j\ge 0}{\overset{}{\sum }}{\displaystyle \underset{n-2j-4=0}{\overset{j}{\sum }}\left(\begin{array}{c}j\\ n-2j-4\end{array}\right)x^{j+2}{y}^n}}\\ ={\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{j=\lfloor \frac{n-4}{3}\rfloor }{\overset{\frac{n-4}{2}}{\sum }}\left(\begin{array}{c}j\\ n-2j-4\end{array}\right)x^{j+1}{y}^n}}-{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{j=\lfloor \frac{n-2}{3}\rfloor }{\overset{\frac{n-2}{2}}{\sum }}\left(\begin{array}{c}j\\ n-2j-2\end{array}\right)x^{j+1}{y}^n}}-{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{j=\lfloor \frac{n-4}{3}\rfloor }{\overset{\frac{n-4}{2}}{\sum }}\left(\begin{array}{c}j\\ n-2j-4\end{array}\right)x^{j+2}{y}^n}}\\ ={\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{k=\lfloor \frac{n-1}{3}\rfloor }{\overset{\frac{n+1}{2}}{\sum }}\left(\begin{array}{c}k-1\\ n-2k-2\end{array}\right)x^k{y}^n}}-{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{k=\lfloor \frac{n+1}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}k-1\\ n-2k\end{array}\right)}}{x}^k{y}^n-{\displaystyle \underset{n\ge 0}{\overset{}{\sum }}{\displaystyle \underset{k=\lfloor \frac{n+2}{3}\rfloor }{\overset{\frac{n}{2}}{\sum }}\left(\begin{array}{c}k-2\\ n-2k\end{array}\right)x^k{y}^n}}.\end{array}$

证毕。

基金项目

国家自然科学基金项目(NO. 12161081)。

NOTES

^*通讯作者。