基于流体方法的排队系统容量设置研究

Research on Capacity Setting of Queuing Sys-tem Based on the Fluid Method

摘要: 在日益多变的市场环境中，提升服务质量对于各大企业来说至关重要。迫于资源有限、需求不定，服务系统常常超负荷运转，导致顾客无效等待严重、服务质量不佳。因此，本文基于容量可变的拥挤型服务系统，考虑顾客多行为模式的存在，构建了基于流体方法的排队系统容量设置模型，以最优化服务质量。通过算法求解及数值分析，验证了该模型对于服务质量提升的价值，并为企业运营提供了指导方向。

Abstract: During the increasingly volatile market environment, improving service quality is crucial for major enterprises. Due to limited resources and uncertain demand, the service system is often overload-ed, resulting in serious customer waiting and poor service quality. In this paper, a capacity setting model based on the fluid method is constructed to improve the service quality for queuing systems with variable capacity, while considering the multi-behavioral patterns of customers. Through algorithm solving and numerical analysis, the value of the model for service quality improvement is verified, and a guiding direction is provided for enterprise operation.

1. 引言

市场环境日趋激烈，服务质量提升已逐步成为各大企业的核心战略之一。迫于资源有限、需求不定，服务系统常常在拥挤环境中运行。由于部分排队队列不可见，顾客无法及时做出正确选择，从而导致无效等待严重、服务质量不佳 [1] 。

在拥挤环境下，顾客重试行为较为强烈 [2] ，传统排队方法已无法完成模型构建及分析。近年来，一类确定型流体方法得到广泛运用，用以准确刻画顾客多行为模式下的排队系统 [3] [4] 。但该方法在轻负载或轻度拥挤情况下准确度不高 [5] [6] 。因此，本文引入了平均资源利用率系数，以克服容量设置变动对流体方法的影响。

本文以容量可变的拥挤型服务系统为研究对象，考虑构建了基于流体方法的容量设置模型，利用蒙特卡洛搜索算法求解稳态方程组，验证了模型的价值并进行了敏感性分析，为企业实践提供了指导方向。

2. 文献综述

服务质量是影响顾客满意度及公司盈利的关键要素之一 [7] 。增加服务资源、提供延迟公告等都能在一定程度上提升服务质量 [8] [9] 。同时，探索容量设置及优化也是可行之策：2020年，胡蓉等 [10] 以休假延迟和Min (N, V)–策略控制的M/G/1排队系统为例，推导稳态队长表达式，讨论了系统容量优化设计问题；2023年，万思燕等人 [11] 研究具有耐烦服务员的M/G/1休假排队系统，推导稳态性能指标，并分析了系统容量优化设计问题。

近年来，关于拥挤型服务系统的研究多集中于顾客多行为模式下的重负载极限推导。2015年，Ding等 [12] 考虑客户重拨及重连接行为，使用流体方法近似排队模型，以推导重负载下的稳态到达率、服务水平和放弃率；2018年，Yu等人 [13] 利用流体近似方法构造了等待提示策略下考虑客户重拨行为的连续排队模型，通过数值分析验证了流体近似方法在重负载环境下的适用性和精确性。

3. 基础模型

3.1. 模型假设

考虑一个容量可变的拥挤型服务系统，如图1所示。系统内共有s个代理，服务规则为先到先服务。假定顾客首次到达服从 $\lambda$ 的泊松分布，所有顾客接受服务过程均服从 $\mu$ 的指数分布。顾客初始耐心值T_k服从 $\gamma$ 的指数分布，其中，k代表顾客在系统中所处位置。假定放弃顾客存在p的概率选择重试，其余则退出系统。为便于分析，假定顾客重试到达服从 $\delta$ 的指数分布，首次到达与重试到达相互独立，且系统所提供的服务完全相同，由于顾客到达方式分为首次和重试，定义 ${\lambda }_0$ 为系统可观测的顾客总到达率。

当顾客到达系统时，若系统总顾客数未超出固定容量N，则该顾客可进入系统。否则，将被迫选择放弃(即被阻塞出系统)，假设p^a(m)为稳态下的阻塞概率，其中m为稳态下系统总顾客数；进入系统后，若存在任意空闲服务台，则该顾客可被立即服务；否则将进入等候区等待；此时，“极端不耐烦”顾客由于耐心程度十分有限，将选择直接放弃；剩余顾客则进入队列开始等待。一旦实际等待时间超出耐心时间，顾客将会选择中途放弃，假定概率为r(n)，其中n为系统中排队等候的顾客数。

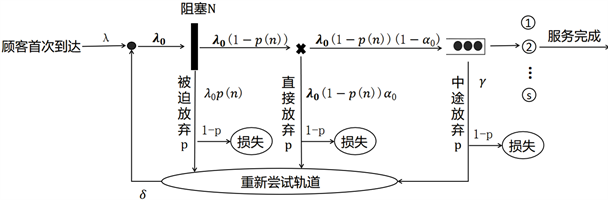
Figure 1. Diagram of the base queuing model considering system capacity settings

图1. 考虑系统容量设置的基础排队模型图示

3.2. 流体模型构建

由于系统负载及顾客的多重行为，使用流体方法近似上述排队模型。考虑系统负载随系统容量变动，本文引入平均资源利用率参数 $c\left(0\le c\le 1\right)$ ，以确保系统容量设置决策的准确性。

定义 $x_1$ ， $x_2$ 分别为稳态下真实顾客人数及重试轨道顾客人数。根据排队分析，可推导出上述排队模型的稳态方程组：

$\{\begin{array}{l}{\lambda }_0\left(1-p^a\left(x_1\right)\right)\left(1-{\alpha }_0\right)r\left(x_1-s\times c\right)=\gamma \left(x_1-s\times c\right)\\ {\lambda }_0\left(1-p^a\left(x_1\right)\right)\left(1-{\alpha }_0\right)-\gamma \left(x_1-s\times c\right)=\mu s\times c\\ p\left({\lambda }_0\left(p^a\left(x_1\right)+\left(1-p^a\left(x_1\right)\right){\alpha }_0\right)+\gamma \left(x_1-s\times c\right)\right)=\delta x_2\\ s.t.x_1\ge s\times c\end{array}$ (3-1)

然后，根据Erlang-A近似公式 [14] 可推导出相关参数：

$p^a\left(m\right)={\displaystyle {\sum }_{i=N}^{\infty }{\pi }_i}$ (3-2)

${\pi }_i=\{\begin{array}{l}{\pi }_s\frac{s!}{i!{\left({\lambda }_0{}^{\text{'}}/\mu \right)}^{s-i}}\begin{array}{cc}& 0\le i\le s\end{array}\\ {\pi }_s\frac{{\left({\lambda }_0{}^{\text{'}}/\gamma \right)}^{s-i}}{{\displaystyle \underset{k=1}{\overset{i-s}{\prod }}\left(\frac{s\mu }{\gamma }+k\right)}}\begin{array}{cc}& i\ge s+1\end{array}\end{array}$ (3-3)

${\pi }_s=\frac{E_{1,s}}{1+\left[A\left(\frac{s\mu }{\gamma },\frac{{\lambda }_0{}^{\text{'}}}{\gamma }\right)-1\right]E_{1,s}}$ (3-4)

其中， ${\lambda }_0^{\text{'}}=\left(1-p\left(m\right)\right)\left(1-{\alpha }_0\right){\lambda }_0$ 代表双轨道环境下顾客的实际到达率， $\rho ={\lambda }_0^{\text{'}}/s\mu$ 代表系统实际负载， $E_{1,s}$ 是指经典Erlang-B模型下的阻塞概率。

$\begin{array}{l}A\left(x,y\right)=1+{\displaystyle \underset{i=1}{\overset{\infty }{\sum }}\frac{y^i}{{\displaystyle {\prod }_{k=1}^i\left(x+k\right)}}}\begin{array}{cc}& \end{array}x>0,y>0\\ E_{1,s}=\frac{\frac{{\left({\lambda }_0^{\text{'}}/\mu \right)}^s}{s!}}{{\displaystyle {\sum }_{i=0}^s\frac{{\left({\lambda }_0^{\text{'}}/\mu \right)}^i}{i!}}}\end{array}$ (3-5)

定义实际等待时间为 $d_n$ ，可近似为虚拟等待时间的平均值 $D_n$ ，则有：

$d_n=E\left(D_n\right)={\displaystyle \underset{i=0}{\overset{n}{\sum }}\frac{1}{s\mu +i\gamma }}$ (3-6)

$\begin{array}{c}r\left(n\right)=P\left(T_k<d_n\right)=1-e^{-\gamma d_n}\\ =1-e^{-\gamma }{}^{E\left(D_n\right)}=1-e^{-\gamma {\displaystyle {\sum }_{i=0}^n\frac{1}{s\mu +i\gamma }}}\end{array}$ (3-7)

$x_1=L={\displaystyle \underset{i=0}{\overset{\infty }{\sum }}i{\pi }_i}$ (3-8)

$x_2=\frac{{\lambda }_0-\lambda }{\delta }$ (3-9)

$c=\frac{{\displaystyle {\sum }_{i=0}^{s-1}i{\pi }_i+s\times \left(1-{\displaystyle {\sum }_{i=0}^{s-1}i{\pi }_i}\right)}}{s}$ (3-10)

以限定时间内服务顾客数为服务质量评定的标准，定义限定时间内完成服务的顾客为优质服务顾客。令T为系统限定的服务完成时间， $P_w$ 为顾客在限定时间T内被服务的概率， $P\left\{Ab\right\}$ 为顾客中途退出的概率， $P\left(W\le T\right)$ 为顾客等待时间小于等于T的概率，则：

$P_w=P\left\{W\le T;Sr\right\}=\left(1-P\left\{Ab\right\}\right)\times P\left(W\le T\right)$ (3-11)

$\begin{array}{c}P\left\{Ab\right\}=P\left[Ab|W>0\right]\times P\left\{W>0\right\}\\ =\left(\frac{1}{\rho A\left(s\mu /\gamma ,{\lambda }_0^{\text{'}}/\gamma \right)}+1-\frac{1}{\rho }\right)\times \frac{A\left(s\mu /\gamma ,{\lambda }_0^{\text{'}}/\gamma \right)E_{1,s}}{1+\left(A\left(s\mu /\gamma ,{\lambda }_0^{\text{'}}/\gamma \right)-1\right)E_{1,s}}\end{array}$ (3-12)

$P\left\{W\le T\right\}={\displaystyle {\sum }_{i=0}^x{\pi }_i}$ (3-13)

其中， $x=s+n_1$ 。根据式(3-6)，通过遍历法可求出 $n_1$ 的值。

定义 $P_B$ ， $P_R$ ， $P_S$ ， $P_L$ ，顾客的直接放弃概率，中途放弃概率，服务顾客概率，以及损失顾客概率。其表达式推导如下：

$P_B=p^a\left(m\right)+\left(1-p^a\left(m\right)\right){\alpha }_0$ (3-14)

$P_R=\left(1-p^a\left(m\right)\right)\left(1-{\alpha }_0\right)r\left(n\right)$ (3-15)

$P_S=1-P_B-P_R$ (3-16)

$P_L=\left(1-p\right)\left(p^a\left(m\right)+\left(1-p^a\left(m\right)\right){\alpha }_0+\left(1-p^a\left(m\right)\right)\left(1-{\alpha }_0\right)r\left(n\right)\right)$ (3-17)

4. 数值分析

以容量可变的拥挤型呼叫中心为例进行数值分析，设计蒙特卡洛算法并利用PyCharm求解计算。全局参数固定为：系统服务人员数目 $s=20$ ，顾客接受服务服从 $\mu =1$ 的指数分布，“极端不耐烦顾客”的比例 $\alpha =0.05$ ，顾客初始耐心值服从 $\gamma =0.8$ 的指数分布，重试行为服从 $\delta =0.5$ 的指数分布。对比分析主要性能指标：优质服务顾客数目(Well-Served)、总服务顾客数(Total-Served)、总损失顾客数(Total-Lost)、直接放弃顾客数(Balking)、中途退出顾客数(Reneging)、重试顾客数(Retrying)。

首先，令系统负载 $\lambda =30$ ，顾客选择重试的概率 $p=0.5$ ，限定完成服务时间 $T=0.5$ ，探索容量设置策略对于服务质量的影响。

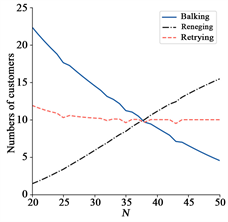
Figure 2. Impact of system capacity settings on service quality and customer behavior

图2. 系统容量设置对于服务质量和顾客行为的影响

如图2，在实验数据范围内，随着容量设置值增大，优质服务顾客数目呈现先增后减的趋势，顾客行为也会受到明显影响。随着N的不断增大，直接放弃顾客数逐步减少，中途放弃顾客数逐步增加，重试顾客数略微减少。同时，由于蒙特卡洛的仿真搜索特性，各指标曲线并不完全光滑。

4.1. 限定服务时间的敏感性分析

Table 1. Results under different limited times

表1. 不同限定完成时间下的结果

考虑到不同系统的需求，分析不同限定完成服务时间下的容量设置策略。固定 $\lambda =30$ ， $p=0.5$ ，限定时间 $T\in \left\{0.1,0.3,0.5,0.8,1.0\right\}$ 。结果如表1所示。

观察表格数据可知：随着系统限定完成服务时间的增大，最佳系统容量值 $N^{*}$ 逐步增大，系统服务质量也越来越好。当服务时间非常紧迫时，适当减小系统容量，可以引导更多耐心不足的顾客尽早离开，为进入系统的顾客争取足够的服务资源；而当时间较为宽松时，服务系统可适当扩大系统容量，让更多顾客进入系统等待，以系统争取更多的服务机会。

4.2. 初始到达率下的敏感性分析

令限定时间 $T=0.5$ ，顾客重试概率 $p=0.5$ ，初始到达率 $\lambda \in \left\{22,25,30,35,40\right\}$ 。

Figure 3. Optimal system capacity value for different initial arrival rates

图3. 不同初始到达率下的最佳系统容量值设置

根据上图3可知：1) 无论顾客的初始到达率为何值，该服务质量优化模型都能计算出最佳的系统容量值 $N^{*}$ ，使得系统的服务质量最佳；2) 对于系统负载越大的系统而言，系统容量的设置尤为重要，如 $\lambda =40$ 时，N的变动使得优质服务顾客数变化非常明显；3) 随着顾客初始到达率的不断增大，最佳系统容量设置值 $N^{*}$ 应适当减小。由于顾客到达率的不断增大，系统非常拥挤，因此限制系统容量可以劝退顾客，以免产生无效等待和不满情绪。

4.3. 重试行为的敏感性分析

分析最佳系统容量值对于顾客选择重试的概率的敏感程度，固定限定时间 $T=0.5$ ，初始到达率 $\lambda =30$ ，顾客重试概率 $p\in \left\{0,0.3,0.5,0.8\right\}$ 。

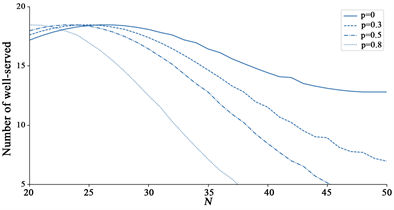
Figure 4. Effect of retry probability on the optimal system capacity setting value

图4. 重试概率对最佳系统容量设置值的影响

如图4，随着重试概率的增大，最佳系统容量设置值 $N^{*}$ 逐步变小。当顾客选择重试的概率越大时，即便顾客因为阻塞放弃掉，也会极大概率选择重试，因此，系统容量值应设置得更小，以便系统资源能更好地服务于耐心充足的顾客；而如果顾客选择重试的概率越小，意味着其一旦放弃便大概率退出系统，此时，将系统容量设置得更大以免顾客流失从而造成服务资源的浪费。

Table 2. Impact of retry behavior on optimal system capacity settings under different loads

表2. 不同负载下重试行为对最佳系统容量设置值的影响

考虑到不同负载下顾客选择重试的概率，进一步探索不同负载下重试行为对最佳系统容量设置值的影响：固定参数 $T=0.5$ ， $p\in \left\{0,0.3,0.5,0.8\right\}$ ， $\lambda \in \left\{22,25,30,40,50\right\}$ 。模型结果如表2所示。

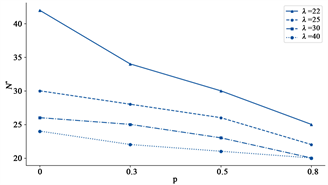
Figure 5. Impact of retry probability under different loads

图5. 不同负载下重试概率的影响分析

结合表2和图5分析可知：1) 无论p值如何变动，该流体模型都能帮助计算出最佳的系统容量值，从而使得系统服务质量水平较为平稳。2) 相较于重拥挤型服务系统而言，系统容量有限的轻拥挤型服务系统需更加关注顾客重试概率的变化：以 $\lambda =22$ 为例，当顾客重试概率p从0增加到0.8时，最佳系统容量值 $N^{*}$ 的变化幅度较大。

5. 结论与展望

基于容量可变的拥挤型服务系统，本文利用Fluid方法构建了容量设置优化模型，证实了该模型对于服务质量提升的意义。通过分析，得出以下几点结论：1) 一旦系统参数固定，该容量设置模型均能帮助获取最佳系统容量值，从而提升服务质量；2) 当限定完成时间较短、顾客的初始到达率较大、顾客重试行为更明显时，最佳系统容量值更小；3) 相较于重拥挤型服务系统而言，系统容量有限的轻拥挤型服务系统需更加注重顾客重试概率的变化。在未来研究中，可进一步优化服务评估方法、改进流体模型，并追求服务质量和服务效率的统一。

参考文献

NOTES

^*通讯作者。