用新激活函数加快新ZNN模型求解时变矩阵Moore-Penrose逆

Accelerating the New ZNN Model to Solve the Moore-Penrose Inverse of Time-Varying Matrix by Using a New Activation Function

摘要: 基于梯度的神经网络(GNN)和张神经网络(ZNN)是两种可用于求解时变矩阵Moore-Penrose逆问题的递归神经网络。与GNN相比，ZNN的计算精度更高。此外，本文提出了一种新的ZNN模型。因此，本文主要利用带有新优化激活函数的ZNN模型来求解时变行满秩(或列满秩)矩阵Moore-Penrose逆问题。这种带有新优化激活函数的ZNN模型可以在有限时间内加速求解时变矩阵的Moore-Penrose逆。通过Lyapunov理论分析，得到了收敛时间的上限。仿真结果进一步证实了理论分析，并证明了采用新优化的激活函数的ZNN模型在求解时变矩阵Moore-Penrose逆时的有效性。

Abstract: Gradient-based neural networks (GNN) and Zhang neural networks (ZNN) are two types of recurrent neural networks that can be used to solve online time-varying matrix Moore-Penrose inverse problems. Compared with GNN, ZNN has higher computational accuracy. Moreover, a new ZNN model is proposed in this paper. Therefore, this paper focuses on solving the online time-varying full row-rank (or full column-rank) matrix Moore-Penrose inverse by using ZNN models with newly optimized activation functions. This ZNN model with the newly optimized activation functions can accelerate the Moore-Penrose inverse of time-varying matrices in finite time. An upper bound on the convergence time is obtained by Lyapunov theoretical analysis. Simulation results further confirm the theoretical analysis and demonstrate the effectiveness of the ZNN model with the newly optimized activation functions for solving time-varying matrix Moore-Penrose inverse.

1. 引言

设 $A\in R^{m\times n}$ 表示为一个定义在实数域上 $m\times n$ 阶的矩阵，如果矩阵 $X\in R^{n\times m}$ 可以同时满足以下四个方程：

1) $AXA=A$ , 2) $XAX=X$ , 3) ${\left(AX\right)}^{\text{T}}=AX$ , 4) ${\left(XA\right)}^{\text{T}}=XA$ ,

其中 $A^{\text{T}}$ 称为矩阵A的转置。称矩阵X是矩阵A的Moore-Penrose逆 [1] 。根据Moore-Penrose逆的性质，可以得到新的方程：

1) $A^{\text{T}}AX=A$ , 2) $XA{A}^{\text{T}}=X$

因此，对于一个给定的行满秩(或列满秩)矩阵 $A\in R^{m\times n}$ ，由于 $A^{\text{T}}A$ 和 $A{A}^{\text{T}}$ 是非退化的，矩阵A的Moore-Penrose逆可以写成以下形式：

$A^{†}=\{\begin{array}{l}{A}^{\text{T}}{\left(A{A}^{\text{T}}\right)}^{-1},m<n;\\ A^{-1},m=n;\\ {\left(A^{\text{T}}A\right)}^{-1}{A}^{\text{T}},m>n.\end{array}$

Moore-Penrose逆经常出现在科学与工程领域，如信号处理、优化以及生物学等。因此，为了能够计算出矩阵Moore-Penrose逆，出现了许多算法，如牛顿迭代法、奇异值分解法等。但是，这些方法的弊端在于只能求解恒定矩阵。因此，设计出新的方法来求解时变矩阵的Moore-Penrose逆是十分重要的。

2011年，ZNN模型首次被Zhang等人提出，用来求解时变行满秩(或列满秩)的矩阵的Moore-Penrose逆 [2] 。不同于GNN这种基于梯度算法常用于静态系统的神经网络，ZNN是基于矩阵值的误差函数可用于求解时变问题的神经网络。并且，他们证明了用神经网络计算时变矩阵Moore-Penrose逆时，ZNN模型的准确度会比GNN模型更高。因此，本文参考文献 [3] 中误差函数的构造方法，将Zhang等人提出的模型进行适当变化，研究新模型计算时变矩阵Moore-Penrose的收敛特性。由于矩阵行满秩的性质与列满秩的性质是类似的，本文主要讨论行满秩的情况。由于在机器控制等方面需要用到求解时变矩阵Moore-Penrose逆，因此如何加快模型求解时变问题是值得研究的。

2014年，Liao等人通过设计出一种新型的激活函数来加快ZNN模型的收敛速度，并且通过李雅普诺夫函数计算得出了在使用这种激活函数时，ZNN模型计算时变矩阵Moore-Penrose逆的收敛时间上界 [4] 。为此，可以继续寻找一种新的激活函数，来加快模型的收敛速度。因此，本文将会用到文献 [4] 中的激活函数以及一种新激活函数：

a) Li激活函数：

$f\left(x\right)=a_1{\left|x\right|}^k\text{sign}\left(x\right)+a_3{\left|x\right|}^{\frac{1}{k}}\text{sign}\left(x\right)$ ,

其中， $a_1,a_3>0$ ， $0<k<1$ ， $\text{sign}\left(x\right)$ 表示符号函数。

b) 激活函数：

$f\left(x\right)=a_1{\left|x\right|}^k\text{sign}\left(x\right)+a_{2}x+a_3{\left|x\right|}^{\frac{q}{k}}\text{sign}\left(x\right)$ ,

其中， $a_1,a_2,a_3>0$ ， $0<k<1$ ， $0<q<k$ 。

本文根据将现有激活函数进行改进来加快神经网络的收敛，并且提出了两种新的ZNN模型来研究求解时变矩阵Moore-Penrose逆的收敛性。

2. 模型设计

当矩阵是行满秩的时候，根据Zhang所提出的误差函数：

$E\left(t\right)=X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)-A^{\text{T}}\left(t\right)$ ,

其中t表示时间， $X\left(t\right)$ 就是所要求解的时变矩阵 $A\left(t\right)$ 的Moore-Penrose逆。并且他给出了误差函数的求导公式 [2] ：

$\stackrel{\dot{}}{E}\left(t\right)=-\Gamma \phi \left(E\left(t\right)\right)$ , (1)

其中设计参数 $\gamma$ ( $\gamma \in R$ , $\gamma >0$ )是影响神经网络收敛速度的一个重要因素，通常都会将他设计的充分大。由此，可以通过将现有的误差函数进行修改，可以得到以下两种新的误差函数：

$E\left(t\right)=X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)-A^{\text{T}}\left(t\right)A\left(t\right)$ , (2)

$E\left(t\right)=X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)-A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)$ , (3)

接着，对上式的两种误差函数分别进行求导，可以得到如下对应的ZNN模型：

$\begin{array}{c}\stackrel{\dot{}}{X}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)=-\Gamma \phi \left(X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)-A^{\text{T}}\left(t\right)A\left(t\right)\right)+{\stackrel{\dot{}}{A}}^{\text{T}}\left(t\right)A\left(t\right)+A^{\text{T}}\left(t\right)\stackrel{\dot{}}{A}\left(t\right)\\ -X\left(t\right)\left(\stackrel{\dot{}}{A}\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)+A\left(t\right){\stackrel{\dot{}}{A}}^{\text{T}}\left(t\right)A\left(t\right)+A\left(t\right)A^{\text{T}}\left(t\right)\stackrel{\dot{}}{A}\left(t\right)\right),\end{array}$ (4)

$\begin{array}{l}\stackrel{\dot{}}{X}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)\\ =-\Gamma \phi \left(X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)-A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)\right)+{\stackrel{\dot{}}{A}}^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)\\ -X\left(t\right)(\stackrel{\dot{}}{A}\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)+A\left(t\right){\stackrel{\dot{}}{A}}^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)+A\left(t\right)A^{\text{T}}\left(t\right)\stackrel{\dot{}}{A}\left(t\right)A^{\text{T}}\left(t\right)\\ +A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right){\stackrel{\dot{}}{A}}^{\text{T}}\left(t\right))+A^{\text{T}}\left(t\right)\stackrel{\dot{}}{A}\left(t\right)A^{\text{T}}\left(t\right)+A^{\text{T}}\left(t\right)A\left(t\right){\stackrel{\dot{}}{A}}^{\text{T}}\left(t\right).\end{array}$ (5)

3. 主要结论

引理1 [4] 对于一个给定的光滑时变行满秩(或列满秩)矩阵，当使用一个单调增加的奇函数时，ZNN模型中的状态矩阵X(t)会从任意初始状态收敛到时变矩阵Moore-Penrose逆的理论解。

定理2 对于一个给定的光滑时变行满秩(或列满秩)矩阵，当使用激活函数(b)时，ZNN模型(4)中的状态矩阵 $X\left(t\right)$ 会从任意初始状态收敛到时变矩阵Moore-Penrose逆的理论解，并且这个收敛时间上界 $t_1$ 为：

$t_1\le \{\begin{array}{ll}\frac{2}{\left(1-k\right){\beta }_2}\ln \left(\frac{{\beta }_2}{{\beta }_1}m{\left(0\right)}^{1-k}+1\right),\hfill & m\left(0\right)\le 1\hfill \\ \frac{2k}{\left(k-q\right){\beta }_2}\ln \left(\frac{{\beta }_2}{{\beta }_3}m{\left(0\right)}^{\frac{k-q}{k}}+1\right),\hfill & m\left(0\right)>1\hfill \end{array}$ ;

其中 ${\beta }_1=2\Gamma a_1$ ， ${\beta }_2=2\Gamma a_2$ ， $m\left(0\right)$ 表示初始误差矩阵 $E\left(0\right)$ 矩阵元素中绝对值最大的一个。

证明 令 ${\beta }_1=2\Gamma a_1$ ， ${\beta }_2=2\Gamma a_2$ ， $e_{ij}\left(0\right)$ 表示初始误差矩阵 $E\left(0\right)$ 的第ij个元素， $m\left(0\right)=\max \left\{\left|e_{ij}\left(0\right)\right|\right\}$ ，表示初始误差矩阵元素中绝对值最大的一个。接着根据误差函数定义李雅普诺夫函数 $l_1\left(t\right)={\left|e_r\left(t\right)\right|}^2$ 和 $l_2\left(t\right)={\left|m\left(t\right)\right|}^2$ 。显然，当 $l_2\left(t\right)$ 随着时间t增加趋于0时， $l_1\left(t\right)$ 也能趋于0。因此，接下来只需证明 $l_2\left(t\right)$ 能够随着t的增加而收敛，即只需证明 ${\stackrel{\dot{}}{l}}_2\left(t\right)\le 0$ 。因此，对 $l_2\left(t\right)$ 求导，并根据文献 [3] 中将其放大可得：

${\stackrel{\dot{}}{l}}_2\left(t\right)=-2\Gamma m\left(t\right)\phi \left(m\left(t\right)\right)\le -{\beta }_1{l}_2^{\frac{k+1}{2}}-{\beta }_2{l}_2\left(t\right)-{\beta }_3{l}_2^{\frac{k+q}{2k}}$ . (6)

显然， ${\stackrel{\dot{}}{l}}_2\left(t\right)\le 0$ ，当且仅当 $e\left(0\right)=0$ 时，等式成立。以上证明了误差能在有限时间内收敛，接下来根据文献 [5] ，通过计算的出其收敛时间上界。

1) 当 $m{\left(0\right)}^2\le 1$ 时，不等式(6)可继续放大为：

${\stackrel{\dot{}}{l}}_2\left(t\right)\le -{\beta }_1{l}_2^{\frac{k+1}{2}}-{\beta }_2{l}_2\left(t\right)$ ,

求解这个微分方程可得：

$t_1\le \frac{2}{\left(1-k\right){\beta }_2}\ln \left(\frac{{\beta }_2}{{\beta }_1}m{\left(0\right)}^{1-k}+1\right)$ .

2) 当 $m{\left(0\right)}^2>1$ 时，不等式(6)可继续放大为：

${\stackrel{\dot{}}{l}}_2\left(t\right)\le -{\beta }_2{l}_2\left(t\right)-{\beta }_3{l}_2^{\frac{k+q}{2k}}$ ,

用同样的方法求解这个微分方程不等式，可以得到：

$t_1\le \frac{2k}{\left(k-q\right){\beta }_2}\ln \left(\frac{{\beta }_2}{{\beta }_3}m{\left(0\right)}^{\frac{k-q}{k}}+1\right)$ .

定理3 对于一个给定的光滑时变行满秩(或列满秩)矩阵，当使用激活函数(b)时，ZNN模型(5)中的状态矩阵X(t)会从任意初始状态收敛到时变矩阵Moore-Penrose逆的理论解，并且这个收敛时间上界为：

$t_2\{\begin{array}{ll}\frac{2}{\left(1-k\right){\beta }_2}\ln \left(\frac{{\beta }_2}{{\beta }_1}m{\left(0\right)}^{1-k}+1\right),\hfill & m\left(0\right)\le 1\hfill \\ \frac{2k}{\left(k-q\right){\beta }_2}\ln \left(\frac{{\beta }_2}{{\beta }_3}m{\left(0\right)}^{\frac{k-q}{k}}+1\right),\hfill & m\left(0\right)>1\hfill \end{array}$ ;

证明类似定理2，此处不再赘述。

4. 仿真实验

以下通过两个例子求解一个时变矩阵方程，从而证明了使用两种新的ZNN模型以及新的激活函数求解时变矩阵Moore-Penrose逆能够达到全局收敛。并且，为了比较模型之间的收敛速度以及激活函数改变后收敛速度的改进，以下仿真实验将对理论部分进行验证，假设时变矩阵 $A\left(t\right)$ 和它的时变Moore-Penrose逆矩阵如下所示：

$A\left(t\right)=\left[\begin{array}{ccc}\cos 2t& \sin 2t& -\cos 2t\\ -\sin 2t& \cos 2t& \sin 2t\end{array}\right]$ , $A^{†}\left(t\right)=\left[\begin{array}{cc}0.5\cos 2t& -0.5\sin 2\\ \sin 2t& \cos 2t\\ -0.5\cos 2t& 0.5\sin 2t\end{array}\right]$ .

图1为仿真中的两种ZNN模型中状态矩阵 $X\left(t\right)$ 的轨迹变化，描述了使用激活函数(b)的ZNN(4)和ZNN(5)，用来求解时变矩阵方程时状态矩阵 $X\left(t\right)$ 阶段性的变化(两种模型的参数设定中都将设置为 $\Gamma =1000$ ， $a_1=1.1$ ， $a_2=1.2$ ， $a_3=1$ ， $k=0.9$ ， $q=0.01$ )。图中的红色虚线对应的是方程的理论解而蓝色实线对应的是状态矩阵实际解。可以看到，图中的实线与虚线会经过一段时间后重合，这就意味着状态矩阵 $X\left(t\right)$ 会从任意初始状态 $X\left(0\right)$ (在仿真实验时不妨设 $X\left(0\right)=\left[1.10.8;0.90.5;1.80.6\right]$ )，最终收敛到时变矩阵方程的理论解 $A^{†}\left(t\right)$ 。

(a) (b)

Figure 1. Trajectories of the state matrix X(t) of two ZNN models. (a) Theoretical and practical solutions of X(t) in ZNN(4); (b) Theoretical and practical solutions of X(t) in ZNN(5)

图1. 两种ZNN模型中的X(t)轨迹变化。(a) ZNN(4)中X(t)的理论解和实际解；(b) ZNN(5)中X(t)的理论解和实际解

但是，在实际生活中理论解与实际解之间普遍存在误差，因此需要将误差控制的尽可能的小。所以，可以将误差用 ${\Vert X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)-A^{\text{T}}\left(t\right)A\left(t\right)\Vert }_F$ 和 ${\Vert X\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)-A^{\text{T}}\left(t\right)A\left(t\right)A^{\text{T}}\left(t\right)\Vert }_F$ 来近似估计理论解和实际解之间的估计误差。在激活函数方面，由于用激活函数(b)来求解时变矩阵方程时，误差的收敛速度会逐渐增快。将激活函数(b)通过理论计算也可以算出对应的收敛时间上界。因此，用它来和之前的Li激活函数作比较，先通过上述所假设的初始状态矩阵的取值，可以得到对应的初始误差矩阵为 $E\left(0\right)=\left[1.20.8-1.2;1.8-0.5-1.8;4.60.6-4.6\right]$ ，式子中对应的最大项 $m\left(0\right)=4.6$ ，将上述激活函数所设置的参数应用到ZNN(4)中，若使用激活函数(a)可通过文献 [3] 计算得出对应的收敛时间上界为 $t\approx 0.0116\left(\text{s}\right)$ 。若使用激活函数(b)，同样可以通过计算得到 $t_1\approx 0.002\left(\text{s}\right)$ 。图2为仿真中对应ZNN(4)分别使用两种不同激活函数的收敛性比较。通过图2可以看出，当ZNN(4)模型使用两种不同的激活函数时，他们都可以在收敛时间上界内完成收敛，符合预期。并且，激活函数(b)的收敛速度优于激活函数(a)。

图3为仿真中设计参数 $\gamma$ 的收敛性比较，可以看出当使用ZNN(4)模型求解时变矩阵Moore-Penrose逆时，设计参数 $\gamma$ 与收敛速度的变化情况(其他参数保持不变)。显然，可以看到收敛速度会随着设计参数 $\gamma$ 的增加而逐渐增加。

Figure 2. Convergence comparison of two activation functions of ZNN(4)

图2. ZNN(4)中两种激活函数的收敛性比较

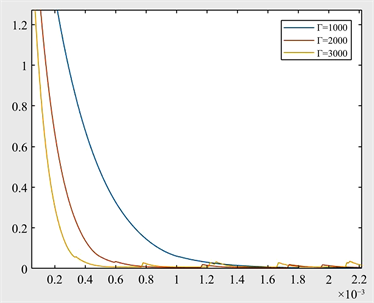
Figure 3. Convergence comparison of parameter Γ in ZNN(4)

图3. ZNN(4)中参数Γ收敛性比较

下面考虑使用ZNN(5)模型时，参数改变对ZNN模型求解时变矩阵Moore-Penrose逆收敛性的影响。与上述ZNN(4)实验类似，当初始状态矩阵不变，可通过计算得ZNN(5)的初始误差矩阵 $E\left(0\right)=\left[2.40.8;3.6-0.5;9.20.6\right]$ ，式子中的最大项 $m\left(0\right)=9.2$ 。将激活函数(a)和(b)分别应用到该模型后，根据文献 [3] 可计算得到使用激活函数(a)后得收敛时间上限为 $t\approx 0.015\left(\text{s}\right)$ 。若使用激活函数(b)，同样可以通过计算得到 $t_1\approx 0.002\left(\text{s}\right)$ 。图4为仿真实验中ZNN(5)中两种激活函数得收敛性比较，可以看出用ZNN(5)模型求解时变矩阵Moore-Penrose逆时，模型得实际收敛时间总是在理论收敛时间内的，符合预期。并且，可以看出使用激活函数(b)的收敛速度总是快于激活函数(a)的。

图5为仿真实验中设计参数Γ的收敛性比较，描述了用ZNN(5)模型求解时变矩阵Moore-Penrose逆时，参数Γ对模型收敛性的影响。在计算收敛时间上界时，可以发现收敛速度会随着处于分母位置的 得增大而减小。从图5中也可以看出，Γ越大，误差的收敛速度越快，证实了这一猜测。

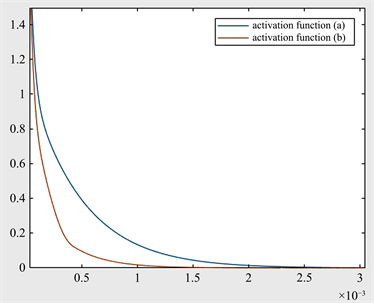
Figure 4. Convergence comparison of two activation functions in ZNN(5)

图4. ZNN(5)中两种激活函数的收敛性比较

Figure 5. Convergence comparison of parameter Γ in ZNN(5)

图5. ZNN(5)中参数Γ收敛性比较

5. 结语

本研究针对时变矩阵方程求解，基于新的误差函数提出了新的ZNN模型，并且将一种新的激活函数应用到该模型中，通过理论分析计算出了收敛时间上界。并且这种激活函数和现有的一种激活函数相比，有着更快的收敛速度。并且通过对模型中参数的研究，可以发现模型的收敛速度会随着参数Γ的增加而加快。理论分析和实验仿真证明了这种方法的有效性。但是由于这种激活函数是非线性的，因此使用这种激活函数还存在着计算复杂度更高这一弊端。未来的研究可能会考虑噪声对两种模型的影响以及扩大矩阵维度运算。

基金项目

国家自然科学基金(No. 12001368)。

NOTES

^*通讯作者。