一种求解带小参数的常微分方程的简化多尺度法

A Simplified Multiscale Method for Solving Ordinary Differential Equations with Small Parameters

摘要: 针对带小参数的微分方程求数值解已经有了很多种数值解法，比如多尺度法(Multiscale Methods)，将微分方程按照时间尺度进行划分，通过分开求解不同时间尺度下的子方程从而求解原方程。但是这种方法划分的尺度过于臃肿，极大的增加了运算时间；其次需要手动处理尺度方程，来避免久期项(secular terms)的影响导致最终求得的数值解有一定的误差。本文提出了一种改进版的多尺度法(Reductive Multiscale Methods)，将时间尺度的划分极大地简化，其次利用欧拉公式和泰勒展开的性质将久期项(secular terms)化到尺度方程内部，从而避免了久期项(secular terms)对数值解的影响。最后将该方法举例得到的数值解与多尺度法(Multiscale Methods)对比，在一定程度下，验证了改进算法的运算量小、高效率的优势。

Abstract: There are many numerical solutions available for solving differential equations with small parame-ters, such as the Multiscale Methods, which divide the differential equations into time scales and solve the original equation by solving sub equations at different time scales separately. However, the scale of this method is too cumbersome, greatly increasing the computational time. Secondly, it is necessary to manually process the scale equation to avoid the influence of the duration term, which may lead to certain errors in the final solution. This article proposes an improved version of the Reduced Multiscale Methods, which greatly simplifies the division of time scales. Secondly, Tay-lor expansion and Euler formula are used to transform the duration terms into the scale equation, thereby avoiding the influence of the duration terms on the numerical solution. Finally, the numer-ical solution obtained by this method was compared with the multiscale methods, thereby verifying to some extent the advantages of the improved algorithm in terms of low computational complexity and high efficiency.

1. 引言

近年来，随着数学和物理的不断发展，非线性振动理论在工程数学中有着越来越广泛的应用，同时从非线性方程中提出的一些数学模型，例如：Duffing方程、Vanderpool方程、和Mathieu方程，在非线性动力学理论中占有很重要的地位，其中一种带小参数的微分方程摄动系统吸引了大家的注意力。由于小参数的影响，摄动方程系统会随之引起波动。

利用何种数学方法来尽量减少小参数对微分方程的影响？近年来国内外针对此求解提出了很多进一步的方法。比如摄动法，或称小参数法，是将非线性因素作为对线性系统的一种摄动，从而在线性解的基础上寻求非线性系统近似解，适用于求解小参数的弱非线性振动系统近似解。为了减少误差，提高系统近似解的精确度，又在摄动法的基础上提出了平均法：近似解形式上与线性系统相同，但是振幅和相位不是常数，而是时间的慢变函数。即将近似解基波的振幅和相位对时间t求导，视作t的函数，并且用一个周期内的平均值作为该函数的近似值。虽然算法简洁计算迅速，但是应用面过于狭窄，无法求解多个精度条件下的系统近似解。

1988年由Diperna R J [1] 和Lions P L [2] 在研究Boltzmann方程时引进的，提出了重正规化法没有考虑到频率对非线性性质的非线性依赖关系。为了考虑这种影响，对自变量引进尺度变量。1999年数学家昂利·庞加莱与安德斯·林德斯泰特 [3] 提出的Lindstedt-Poincare法，是摄动理论中一种当正则摄动法失效时求解常微分方程的近似周期解的方法。于是多尺度法 [4] 应运而生，该方法的核心思想是正则运动在长时间下近似解失效，甚至出现久期项，时间趋向于无穷大时发散，为解决这个问题，引入多重尺度，来分别处理短时间扰动项效应和长时间扰动项效应。数学家基本上一直在如何处理久期项上，不断改进自己的方法，来避免最终算出的系统近似解误差过大。

2. 多尺度法

考虑如下带初始条件的非线性常微分方程(Duffing方程) [5]

$\frac{{\text{d}}^{2}y}{\text{d}{t}^2}+y+\epsilon y^3=0$

$y\left(0\right)=1$

$\frac{\text{d}y}{\text{d}t}\left(0\right)=1$ (2.1)

这里t是关于y的函数 $\epsilon$ 代表小参数。

我们利用多尺度法展开以下形式：

$\begin{array}{c}y\left(t\right)={\displaystyle \underset{n=0}{\overset{N}{\sum }}{\epsilon }^n{y}_n}\left(t_0,t_1,t_2,\cdots \right)\\ =y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+{\epsilon }^2{y}_2\left(t_0,t_1,t_2,\cdots \right)+\cdots \end{array}$ (2.2)

这里时间尺度 $t_0=t;t_1=\epsilon t;t_2={\epsilon }^{2}t;\cdots ;t_n={\epsilon }^{n}t\left(n=0,1,2,3,\cdots ,N\right)$ 。

显然有

$\frac{\text{d}}{\text{d}t}={\partial }_{t_0}+\epsilon {\partial }_{t_1}+{\epsilon }^2{\partial }_{t_2}+\cdots$ (2.3)

将(2.2)和(2.3)代入到方程(2.1)中

$\begin{array}{l}\left({\partial }_{t_0}+\epsilon {\partial }_{t_1}+{\epsilon }^2{\partial }_{t_2}+\cdots \right)\left({\partial }_{t_0}+\epsilon {\partial }_{t_1}+{\epsilon }^2{\partial }_{t_2}+\cdots \right)\\ \left(y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+{\epsilon }^2{y}_2\left(t_0,t_1,t_2,\cdots \right)+\cdots \right)\\ +y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+{\epsilon }^2{y}_2\left(t_0,t_1,t_2,\cdots \right)+\cdots \\ +\epsilon {\left(y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+{\epsilon }^2{y}_2\left(t_0,t_1,t_2,\cdots \right)+\cdots \right)}^3=0\end{array}$

整理得

$\begin{array}{l}\left({\partial }_{t_0{t}_0}+\epsilon \left({\partial }_{t_0{t}_1}+{\partial }_{t_1{t}_0}\right)+{\epsilon }^2\left({\partial }_{t_0{t}_2}+{\partial }_{t_1{t}_1}+{\partial }_{t_2{t}_0}\right)+\cdots \right)\\ \left(y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+{\epsilon }^2{y}_2\left(t_0,t_1,t_2,\cdots \right)+\cdots \right)\\ +\left(y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+{\epsilon }^2{y}_2\left(t_0,t_1,t_2,\cdots \right)+\cdots \right)\\ +\epsilon y_0\left(t_0,t_1,t_2,\cdots \right)+3{\epsilon }^2{y}_0{\left(t_0,t_1,t_2,\cdots \right)}^2{y}_1\left(t_0,t_1,t_2,\cdots \right)+\cdots =0\end{array}$

↓

$\begin{array}{l}{\partial }_{t_0{t}_0}{y}_0\left(t_0,t_1,t_2,\cdots \right)+y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon ({\partial }_{t_0{t}_0}{y}_1\left(t_0,t_1,t_2,\cdots \right)+y_1\left(t_0,t_1,t_2,\cdots \right)\\ +{\partial }_{t_0{t}_1}{y}_0\left(t_0,t_1,t_2,\cdots \right)+{\partial }_{t_1{t}_0}{y}_0\left(t_0,t_1,t_2,\cdots \right))+{\epsilon }^2({\partial }_{t_0{t}_0}{y}_2\left(t_0,t_1,t_2,\cdots \right)+y_2\left(t_0,t_1,t_2,\cdots \right)\\ +{\partial }_{t_0{t}_1}{y}_1\left(t_0,t_1,t_2,\cdots \right)+{\partial }_{t_1{t}_0}{y}_1\left(t_0,t_1,t_2,\cdots \right)+{\partial }_{t_0{t}_2}{y}_0\left(t_0,t_1,t_2,\cdots \right)+{\partial }_{t_1{t}_1}{y}_0\left(t_0,t_1,t_2,\cdots \right)\\ +{\partial }_{t_2{t}_0}{y}_0\left(t_0,t_1,t_2,\cdots \right))+\cdots +\epsilon y_0\left(t_0,t_1,t_2,\cdots \right)+3{\epsilon }^2{y}_0{\left(t_0,t_1,t_2,\cdots \right)}^2{y}_1\left(t_0,t_1,t_2,\cdots \right)+\cdots =0\end{array}$ (2.4)

按照时间尺度t划分为 $t\le {\epsilon }^0、t\le {\epsilon }^1、t\le \cdots$ 得到以下时间尺度方程：

当时间尺度为 $t\le {\epsilon }^0$

${\partial }_{t_0{t}_0}{y}_0\left(t_0,t_1,t_2,\cdots \right)+y_0\left(t_0,t_1,t_2,\cdots \right)=0$ (2.5)

当时间尺度为 $t\le {\epsilon }^1$

${\partial }_{t_0{t}_0}{y}_1\left(t_0,t_1,t_2,\cdots \right)+y_1\left(t_0,t_1,t_2,\cdots \right)=y_0{\left(t_0,t_1,t_2,\cdots \right)}^3-{\partial }_{t_0{t}_1}{y}_0\left(t_0,t_1,t_2,\cdots \right)-{\partial }_{t_1{t}_0}{y}_0\left(t_0,t_1,t_2,\cdots \right)$ (2.6)

当时间尺度为 $t\le {\epsilon }^2$

$\begin{array}{l}{\partial }_{t_0{t}_0}{y}_2\left(t_0,t_1,t_2,\cdots \right)+y_2\left(t_0,t_1,t_2,\cdots \right)\\ =3y_0{\left(t_0,t_1,t_2,\cdots \right)}^2{y}_1\left(t_0,t_1,t_2,\cdots \right)-{\partial }_{t_0{t}_1}{y}_1\left(t_0,t_1,t_2,\cdots \right)-{\partial }_{t_1{t}_0}{y}_1\left(t_0,t_1,t_2,\cdots \right)\\ -{\partial }_{t_1{t}_1}{y}_0\left(t_0,t_1,t_2,\cdots \right)-{\partial }_{t_2{t}_0}{y}_0\left(t_0,t_1,t_2,\cdots \right)\end{array}$ (2.7)

对(2.5)求解得

$y_0\left(t_0,t_1,t_2,\cdots \right)=A_0\left(t_1,t_2,t_3,\cdots \right){\text{e}}^{i{t}_0}+(\ast )$ (2.8)

这里时间尺度 $t_0=t;t_1=\epsilon t;t_2={\epsilon }^{2}t;\cdots ;t_n={\epsilon }^{n}t\left(n=0,1,2,3,\cdots ,N\right)$

$(\ast )$ 是 $A_0\left(t_1,t_2,t_3,\cdots \right){\text{e}}^{i{t}_0}$ 的共轭，即

$(\ast )=A_0^{\text{*}}\left(t_1,t_2,t_3,\cdots \right){\text{e}}^{-i{t}_0}$ (2.9)

将(2.8)代入到尺度方程(2.6)中

${\partial }_{t_0{t}_0}{y}_1\left(t_0,t_1,t_2,\cdots \right)+y_1\left(t_0,t_1,t_2,\cdots \right)=\left(3{\left|A_0\right|}^2{A}_0-2i{\partial }_{t_1}{A}_0\right){\text{e}}^{it}+A_0^3{\text{e}}^{3it}+(\ast )$ (2.10)

这里出现了久期项，或者叫做永年项(secular terms)。这里引入secular terms的定义：

定义1.1：我们把 $f\left(t\right)$ 称为永年项(secular terms) [6] ，如果当 $t\to 0$ 时， $f\left(t\right)$ 无界；换言之：

$f\text{are}\text{secularterms}:=\forall T>0,\forall C>0,\exists t>T:\left|f\left(t\right)\right|>C$

从力学角度来看，当时间t趋近于无穷时，表现出的意义便是系统振幅无穷大，进而能量无穷大，频率相等的项会引起共振，显然这是不可能的。在微分方程的求解中，即使齐次解本身是有界的，永年项(secular terms)的出现会导致非齐次解的无界性。因此求解过程中便想通过控制参数意图消除这样的“永年项(久期项)”，从而减少数值解的误差。

$3{\left|A_0\right|}^2{A}_0-2i{\partial }_{t_1}{A}_0=0$

${\partial }_{t_1}{A}_0=-\frac{3i}{2}{\left|A_0\right|}^2{A}_0$ (2.11)

方程(2.10)化为

${\partial }_{t_0{t}_0}{y}_1\left(t_0,t_1,t_2,\cdots \right)+y_1\left(t_0,t_1,t_2,\cdots \right)=A_0^3{\text{e}}^{3it}+(\ast )$ (2.12)

$y_1\left(t_0,t_1,t_2,\cdots \right)=-\frac{1}{8}{A}_0^3{\text{e}}^{3it}+(\ast )$ (2.13)

将(2.8)、(2.13)代入到(2.7)中

${\partial }_{t_0{t}_0}{y}_2\left(t_0,t_1,t_2,\cdots \right)+y_2\left(t_0,t_1,t_2,\cdots \right)=\left(-\frac{3}{8}{\left|A_0\right|}^4{A}_0-2i{\partial }_{t_2}{A}_0-{\partial }_{t_1{t}_1}{y}_1\right){\text{e}}^{it}+NST$ (2.14)

其中NST [7] 是“非特殊术语”的缩写，方程(2.14)考虑的是在时间尺度 $t\le {\epsilon }^2$ 时。因此我们只需要永年项(secular terms)，并将其余不需要的项分到NST项中。

把(2.14)中永年项(secular terms)取零有

$-\frac{3}{8}{\left|A_0\right|}^4{A}_0-2i{\partial }_{t_2}{A}_0-{\partial }_{t_1{t}_1}{A}_0=0$

$\begin{array}{c}{\partial }_{t_2}{A}_0=\frac{3i}{16}{\left|A_0\right|}^4{A}_0+\frac{i}{2}{\partial }_{t_1{t}_1}{A}_0=\frac{15i}{16}{\left|A_0\right|}^4{A}_0\\ =\frac{3i}{16}{\left|A_0\right|}^4{A}_0-\frac{i}{2}{\partial }_{t_1}\left(-\frac{3i}{2}{\left|A_0\right|}^2{A}_0\right)\\ =\frac{3i}{16}{\left|A_0\right|}^4{A}_0-\frac{i}{2}\frac{9}{4}{\left|A_0\right|}^4{A}_0\\ =-\frac{15i}{16}{\left|A_0\right|}^4{A}_0\end{array}$ (2.15)

当我们划分时间尺度为 $t\le {\epsilon }^2$ ，为了方便令

$A\left(t\right)=A_0\left(t_1,t_2,t_3,\cdots \right)$ (2.16)

方程(2.2)为

$\begin{array}{c}y\left(t\right)=y_0\left(t_0,t_1,t_2,\cdots \right)+\epsilon y_1\left(t_0,t_1,t_2,\cdots \right)+O\left({\epsilon }^2\right)\\ =A\left(t_1,t_2,t_3,\cdots \right){\text{e}}^{it}-\epsilon \frac{1}{8}{A}^3{\text{e}}^{3it}+(\ast )+O\left({\epsilon }^2\right)\end{array}$ (2.17)

通过方程(2.16)发现，想要求出 $y\left(t\right)$ 的解，首先要求函数 $A_0\left(t_1,t_2,t_3,\cdots \right)$ ，有以下方程满足

$\frac{\text{d}A}{\text{d}t}=\left({\partial }_{t_0}+\epsilon {\partial }_{t_1}+{\epsilon }^2{\partial }_{t_2}+\cdots \right)A_0\left(t_1,t_2,t_3,\cdots \right)$

$\frac{\text{d}A}{\text{d}t}={\partial }_{t_0}{A}_0\left(t_1,t_2,t_3,\cdots \right)+\epsilon {\partial }_{t_1}{A}_0\left(t_1,t_2,t_3,\cdots \right)+{\epsilon }^2{\partial }_{t_2}{A}_0\left(t_1,t_2,t_3,\cdots \right)+\cdots$ (2.18)

这里时间尺度 $t_0=t;t_1=\epsilon t;t_2={\epsilon }^{2}t;\cdots ;t_n={\epsilon }^{n}t\left(n=0,1,2,3,\cdots ,N\right)$ 。

保留需要的方程项，截断该方程至时间尺度 $t\le {\epsilon }^2$

$\frac{\text{d}A}{\text{d}t}=0+\epsilon {\partial }_{t_1}{A}_0\left(t_1,t_2,t_3,\cdots \right)+{\epsilon }^2{\partial }_{t_2}{A}_0\left(t_1,t_2,t_3,\cdots \right)$

代入(2.11)和(2.15)

$\frac{\text{d}A}{\text{d}t}=-\epsilon \frac{3i}{2}{\left|A\right|}^{2}A-{\epsilon }^2\frac{15i}{16}{\left|A\right|}^{4}A$ (2.19)

我们对(2.19)两边乘于A的共轭函数 $A^{*}$

$\frac{\text{d}}{\text{d}t}A{A}^{*}=-\epsilon \frac{3i}{2}{\left|A\right|}^{2}A{A}^{*}-{\epsilon }^2\frac{15i}{16}{\left|A\right|}^{4}A{A}^{*}$ (2.20)

同理可得

$\frac{\text{d}}{\text{d}t}A{A}^{*}=\epsilon \frac{3i}{2}{\left|A^{*}\right|}^2{A}^{*}A+{\epsilon }^2\frac{15i}{16}{\left|A^{*}\right|}^4{A}^{*}A$ (2.21)

最后

$\begin{array}{c}\frac{\text{d}}{\text{d}t}{\left|A\right|}^2=\frac{\text{d}}{\text{d}t}A{A}^{*}+\frac{\text{d}}{\text{d}t}A{A}^{*}\\ =-\epsilon \frac{3i}{2}{\left|A\right|}^{2}A{A}^{*}-{\epsilon }^2\frac{15i}{16}{\left|A\right|}^{4}A{A}^{*}+\epsilon \frac{3i}{2}{\left|A^{*}\right|}^2{A}^{*}A+{\epsilon }^2\frac{15i}{16}{\left|A^{*}\right|}^4{A}^{*}A\\ =0\end{array}$ (2.22)

由(2.22)可知 ${\left|A\right|}^2$ 与t无关可视为一个常数，不妨令

${\left|A\right|}^2={\left|A\left(0\right)\right|}^2$ (2.23)

对(2.19)两边对t取积分整理得

$A\left(t\right)=A\left(0\right){\text{e}}^{-\left(\epsilon \frac{3i}{2}{\left|A\right|}^2+{\epsilon }^2\frac{15i}{16}{\left|A\right|}^4\right)t}$ (2.24)

这里代入方程(2.23)

$A\left(t\right)=A\left(0\right){\text{e}}^{-\left(\epsilon \frac{3i}{2}{\left|A\left(0\right)\right|}^2+{\epsilon }^2\frac{15i}{16}{\left|A\left(0\right)\right|}^4\right)t}$ (2.25)

由(2.25)可知，想求出 $A\left(t\right)$ 的解，显然要先求出 $A\left(0\right)$ 的解。

下一步将(2.17)代入到(2.1)的初始条件中

$\{\begin{array}{l}{\left\{A\left(t\right){\text{e}}^{it}-\epsilon \frac{1}{8}A{\left(t\right)}^3{\text{e}}^{3it}+A^{*}\left(t\right){\text{e}}^{-it}-\epsilon \frac{1}{8}{A}^{*}{\left(t\right)}^3{\text{e}}^{-3it}\right\}|}_{t=0}=1\\ \{A^{\prime }\left(t\right)e^{it}+iA\left(t\right){\text{e}}^{it}-\epsilon \frac{3}{8}A{\left(t\right)}^2{A}^{\prime }\left(t\right){\text{e}}^{3it}-\frac{3i}{8}A{\left(t\right)}^3{\text{e}}^{3it}\\ +{A^{*}{}^{\prime }\left(t\right)e^{-it}-i{A}^{*}\left(t\right){\text{e}}^{-it}-\epsilon \frac{3}{8}{A}^{*}{\left(t\right)}^2{A}^{*}{}^{\prime }\left(t\right){\text{e}}^{-3it}+\epsilon \frac{3i}{8}{A}^{*}{\left(t\right)}^3{\text{e}}^{3it}\}|}_{t=0}=0\end{array}$ (2.26)

↓

$\{\begin{array}{l}A\left(0\right)-\epsilon \frac{1}{8}A{\left(0\right)}^3+A^{*}\left(0\right)-\epsilon \frac{1}{8}{A}^{*}{\left(0\right)}^3=1\\ \{A^{\prime }\left(0\right)+iA\left(0\right)-\epsilon \frac{3}{8}A{\left(0\right)}^2{A}^{\prime }\left(0\right)-\frac{3i}{8}A{\left(0\right)}^3\\ +{A^{*}{}^{\prime }\left(0\right)-i{A}^{*}\left(0\right)-\epsilon \frac{3}{8}{A}^{*}{\left(0\right)}^2{A}^{*}{}^{\prime }\left(0\right)+\epsilon \frac{3i}{8}{A}^{*}{\left(0\right)}^3\}|}_{t=0}=0\end{array}$ (2.27)

代入(2.19)和(2.23)

$A^{\prime }\left(0\right)=-\epsilon \frac{3i}{2}{\left|A\left(0\right)\right|}^{2}A\left(0\right)-{\epsilon }^2\frac{15i}{16}{\left|A\left(0\right)\right|}^{4}A\left(0\right)$ (2.28)

将(2.28)代入(2.27)，整理最终得到

$\{\begin{array}{l}A\left(0\right)-\epsilon \frac{1}{8}A{\left(0\right)}^3+A^{*}\left(0\right)-\epsilon \frac{1}{8}{A}^{*}{\left(0\right)}^3=1(2.29)\\ A{\left(0\right)}^2+A^{*}{\left(0\right)}^2=\frac{16}{3\epsilon }(\; 2.30\; )\end{array}$

将(2.30)代入(2.29)中得到一个 $\epsilon$ 关于 $A\left(0\right)$ 的一元多次函数，这里不妨设 $A\left(0\right)=x$

$\frac{{\epsilon }^3}{32}{x}^6-\frac{15{\epsilon }^2}{48}{x}^4+\frac{{\epsilon }^2}{4}{x}^3+\epsilon x^2-2\epsilon x+\epsilon -\frac{16}{27}=0$ (2.31)

我们并不需要求出(2.31)的解，只需要通过(2.30)和(2.31)得到 $\epsilon =0.1$ 、 $\epsilon =0.01$ 、 $\epsilon =0.001$ 时对应的 $A\left(0\right)$ 的值即可。如下表1。

通过求出 $A\left(0\right)$ 在 $\epsilon$ 取不同值时的解，代入到(2.25)中即可得到 $A\left(t\right)$ 的值，从而得到(2.17)中 $y\left(t\right)$ 的解。并在后续环节在一定条件下作图误差分析。

3. 简化多尺度法

在数学中，理解谐振子的运动，实际上是在学习某种微分方程，这种方程式在物理学和其他学科中反复出现。挂在弹簧上的有质量物体的振动、电路中电荷的振荡以及产生声波的音叉的振动等现象，遵循一些类似的方程，这些方程被称作常系数线性微分方程 [8] 。一个常系数线性微分方程中的每一项都是因变量对自变量的微商和一个常数的乘积：

Table 1. The values of A(0) corresponding to ε values

表1. ε取值对应的A(0)的值

$a_n\frac{{\text{d}}^{n}A}{\text{d}{t}^n}+a_{n-1}\frac{{\text{d}}^{n-1}A}{\text{d}{t}^{n-1}}+\cdots +a_1\frac{\text{d}A}{\text{d}t}+a_0=0$ (3.1)

被称作一个n阶常系数线性微分方程。

这里以Duffing方程为例：

$y^{″}\left(t\right)+{\omega }_0^{2}y\left(t\right)=0$ (3.2)

其中 $y\left(t\right)$ 是振荡器在时间t的位移， ${\omega }_0$ 是谐振运动系统的固有频率。

(3.1)的一般解是众所周知的

$y_h\left(t\right)=A\cos \left({\omega }_{0}t\right)+B\sin \left({\omega }_{0}t\right)$

这里A和B是任意常数，可知当所有的 $t\in R$ ，有 $\left|\cos \left({\omega }_{0}t\right)\right|\le 1,\left|\sin \left({\omega }_{0}t\right)\right|\le 1$ 。得到

$\left|y_h\left(t\right)\right|\le A+B$

如果输入一个驱动力，它周期性地以频率 $\omega$ 将能量输入谐振运动系统中，(3.2)的右边就会出现不均匀的振荡

$y^{″}\left(t\right)+{\omega }_0^{2}y\left(t\right)=\cos \left(\omega t\right)$ (3.3)

显然(3.3)的解取决于驱动力的驱动频率 $\omega$ 和谐振运动系统的固有频率 ${\omega }_0$ 。举个例子，这种驱动力可以是一个电磁铁，它被放置在弹簧下面，并产生一个周期性变化的场，以影响悬挂在弹簧上的磁性物质的振荡幅度的变化。

如果 $\left|\omega \right|\to \left|{\omega }_0\right|$ ，也就是驱动力的周期频率 $\omega$ 无限接近谐振运动系统的固有频率 ${\omega }_0$ ；

或者 $\left|\omega \right|\ne \left|{\omega }_0\right|$ ，也就是驱动力的周期频率 $\omega$ 不等于谐振运动系统的固有频率 ${\omega }_0$ ；

会发生什么情况？下面进行分情况讨论：

当 $\left|\omega \right|\ne \left|{\omega }_0\right|$ 时

$y\left(t\right)=A\cos \left({\omega }_{0}t\right)+B\sin \left({\omega }_{0}t\right)+\frac{\cos \left(\omega t\right)}{{\omega }_0^2-{\omega }^2}$ (3.4)

当 $\left|\omega \right|=\left|{\omega }_0\right|$ 时

$y_s\left(t\right)=A\cos \left({\omega }_{0}t\right)+B\sin \left({\omega }_{0}t\right)+\frac{1}{2}t\sin \left(\omega t\right)$ (3.5)

从(3.4)可以发现：等号右边最后一个项分母 $\left|{\omega }_0^2-{\omega }^2\right|\to 0$ 时，由于 $\cos \left(\omega t\right)$ 是有界的，等号右边振荡幅度就会变得越来越大；换言之，当驱动频率 $\omega$ 接近系统的固有频率 ${\omega }_0$ 时，系统从外力中吸收越来越多的能量。

Figure 1. Amplitude y image with t variation

图1. 随着t变化的振幅y图像

令 $A=0,B=1,{\omega }_0=0.5,\omega =0.7$ . 代入到(3.4)和(3.5)，从而得到 $y\left(t\right)$ (红线)和 $y_s\left(t\right)$ (蓝线)，如图1所示。

从图1上显然观察到 $y\left(t\right)$ 在所有的t上都是有界的，而 $y_s\left(t\right)$ 在所有的t上是无界的。我们把引起这种振荡幅度越来越大的，从而导致结果误差越来越大的项称之为久期项，或者叫做永年项(secular terms)，和第一节定义1.1提出的永年项(secular terms)是一个概念，求解微分方程中要意图消除这样的“永年项(久期项)”，从而减少数值解的误差。

下面考虑第一节中同一个带初始条件的非线性常微分方程

$\frac{{\text{d}}^{2}y}{\text{d}{t}^2}+y+\epsilon y^3=0$

$y\left(0\right)=1$

$\frac{\text{d}y}{\text{d}t}\left(0\right)=1$ (3.6)

这里t是关于y的函数 $\epsilon$ 代表小参数。

我们利用简化多尺度法展开为以下形式：

$\begin{array}{c}y\left(t\right)={\displaystyle \underset{n=0}{\overset{N}{\sum }}{\epsilon }^n{y}_n\left(t\right)}\\ =y_0\left(t\right)+\epsilon y_1\left(t\right)+{\epsilon }^2{y}_2\left(t\right)+\cdots \end{array}$ (3.7)

将(3.7)代入(3.6)中有

${\displaystyle \underset{n=0}{\overset{N}{\sum }}{\epsilon }^n{y^{″}}_n\left(t\right)}+{\displaystyle \underset{n=0}{\overset{N}{\sum }}{\epsilon }^n{y}_n\left(t\right)}+\epsilon {\displaystyle \underset{n=0}{\overset{N}{\sum }}{\epsilon }^n{y}_n\left(t\right)}=0$

$={y^{″}}_0\left(t\right)+y_0\left(t\right)+\epsilon \left({y^{″}}_1\left(t\right)+y_1\left(t\right)+y_0^3\left(t\right)\right)+O\left({\epsilon }^2\right)=0$ (3.8)

把(3.8)拆成两个微分方程

$\{\begin{array}{l}{y^{″}}_0\left(t\right)+y_0\left(t\right)=0(3.9\text{a})\\ {y^{″}}_1\left(t\right)+y_1\left(t\right)=-y_0^3\left(t\right)(3.9\text{b})\end{array}$

显然(3.9a)的解为

$y_0\left(t\right)=\cos \left(t\right)$ (3.10)

将(3.10)代入到(3.9b)中

${y^{″}}_1\left(t\right)+y_1\left(t\right)=-{\cos }^3\left(t\right)$ (3.11)

利用三角函数的加法定理

${\cos }^3\left(t\right)=-\frac{1}{4}\cos \left(3t\right)-\frac{3}{4}\cos \left(t\right)$ (3.12)

将(3.12)代入(3.9b)，并拆分成两个线性和非线性微分方程

$\{\begin{array}{l}{y^{″}}_{1a}\left(t\right)+y_{1a}\left(t\right)=-\frac{1}{4}\cos \left(3t\right)(3.13\text{a})\\ {y^{″}}_{1b}\left(t\right)+y_{1b}\left(t\right)=-\frac{3}{4}\cos \left(t\right)(3.13\text{b})\end{array}$

把(3.4)、(3.5)代入到(3.13a)和(3.13b)

$\{\begin{array}{l}{y}_{1a}\left(t\right)=A\cos \left(t\right)+B\sin \left(t\right)-\frac{1}{4}\cdot \frac{\cos \left(3t\right)}{1-3^2}(3.14\text{a})\\ y_{1b}\left(t\right)=C\cos \left(t\right)+D\sin \left(t\right)-\frac{3}{4}\cdot \frac{1}{2}t\sin \left(t\right)(3.14\text{b})\end{array}$

这里A、B、C、D取任意常数

于是有

$\begin{array}{c}{y}_1\left(t\right)=y_{1a}\left(t\right)+y_{1b}\left(t\right)\\ =\tilde{A}\cos \left(t\right)+\tilde{B}\sin \left(t\right)+\frac{1}{32}\cos \left(3t\right)-\frac{3}{8}t\sin \left(t\right)\end{array}$ (3.15)

这里 $\tilde{A}$ 、 $\tilde{B}$ 取任意常数。

将(3.6)中初始条件 $y\left(0\right)=1$ 和 $\frac{\text{d}y}{\text{d}t}\left(0\right)=1$ 代入到(3.15)

$\{\begin{array}{l}\tilde{A}=-\frac{1}{32}\\ \tilde{B}=0\end{array}$ (3.16)

将(3.10)和(3.15)、(3.16)代入到(3.7)中

$\begin{array}{c}y\left(t\right)=y_0\left(t\right)+\epsilon y_1\left(t\right)+O\left({\epsilon }^2\right)\\ =\cos \left(t\right)+\epsilon \left(-\frac{1}{32}\cos \left(t\right)+\frac{1}{32}\cos \left(3t\right)-\frac{3}{8}t\sin \left(t\right)\right)+(\ast )+O\left({\epsilon }^2\right)\end{array}$ (3.17)

发现(3.17)含有 $\epsilon$ 的项仍是一个永年项(secular terms)，下一步要消除掉它。

引入以下概念

$f\left(t\right):={\text{e}}^{-\epsilon t}={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\frac{{\left(-1\right)}^n{\epsilon }^n{t}^n}{n!}}=1-\epsilon t+\frac{1}{2}{\epsilon }^2{t}^2-\frac{1}{6}{\epsilon }^3{t}^3+\frac{1}{24}{\epsilon }^4{t}^4+\cdots +\frac{{\left(-1\right)}^n{\epsilon }^n{t}^n}{n!}$ (3.18)

我们利用泰勒展开的逆变换和欧拉公式 ${\text{e}}^{it}=\cos \left(t\right)+i\sin \left(t\right)$ 将(3.17)中的永年项(secular terms)离散成级数和的形式，即

$A_n{t}^n{\text{e}}^{it}+A_n^{\text{*}}{t}^n{\text{e}}^{-it}$

这里

$A_n=\frac{1}{2}\frac{3i}{8}+\frac{1}{2}\frac{1}{2}\frac{9i}{64}+\cdots =\frac{1}{2}\frac{1}{n!}{\left(\frac{3i}{8}\right)}^n$ (3.19)

最后 $y\left(t\right)$ 化为

$\begin{array}{c}y\left(t\right)={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\epsilon }^n\left\{A_n{t}^n{\text{e}}^{it}+A_n^{*}{t}^n{\text{e}}^{-it}\right\}}\\ ={\displaystyle \underset{n=0}{\overset{\infty }{\sum }}\frac{1}{2}{\epsilon }^n{t}^n}\left(\frac{1}{n!}{\left(\frac{3i}{8}\right)}^n{\text{e}}^{it}+\frac{1}{n!}{\left(-\frac{3i}{8}\right)}^n{\text{e}}^{-it}\right)\\ =\frac{1}{2}\left({\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\epsilon }^n{t}^n}\left(\frac{1}{n!}{\left(\frac{3i}{8}\right)}^n{\text{e}}^{it}\right)+{\displaystyle \underset{n=0}{\overset{\infty }{\sum }}{\epsilon }^n{t}^n}\left(\frac{1}{n!}{\left(-\frac{3i}{8}\right)}^n{\text{e}}^{-it}\right)\right)\\ =\frac{1}{2}\left({\text{e}}^{\frac{3i}{8}\epsilon t}{\text{e}}^{it}+{\text{e}}^{-\frac{3i}{8}\epsilon t}{\text{e}}^{-it}\right)=\frac{1}{2}\left({\text{e}}^{it\left(1+\frac{3}{8}\epsilon \right)}+{\text{e}}^{-it\left(1+\frac{3}{8}\epsilon \right)}\right)\end{array}$ (3.20)

利用欧拉公式 ${\text{e}}^{it}=\cos \left(t\right)+i\sin \left(t\right)$ 将(3.20)化为

$\begin{array}{c}y\left(t\right)=\frac{1}{2}\left(\cos \left(t\left(1+\frac{3}{8}\epsilon \right)\right)+i\sin \left(t\left(1+\frac{3}{8}\epsilon \right)\right)+\cos \left(t\left(1+\frac{3}{8}\epsilon \right)\right)-i\sin \left(t\left(1+\frac{3}{8}\epsilon \right)\right)\right)\\ =\cos \left(t\left(1+\frac{3}{8}\epsilon \right)\right)\end{array}$ (3.21)

最终通过泰勒展开的定义和欧拉公式将永年项(secular terms)化入了整体的函数里面，避免了永年项(secular terms)的出现，导致振荡幅度越来越大，从而使结果误差变得越来越大的风险。

4. 实验结果分析

第一节利用时间尺度t全展开的多尺度法(Multiscale Methods)理论上计算出了在时间尺度 $t\le \frac{1}{{\epsilon }^2}$ 时，考虑当永年项(secular terms)取零，求出了带小参数的常微分方程的数值解；第二节利用只展开时间尺度t的简化多尺度法(Reductive Multiscale Methods)，在时间尺度 $t\le \frac{1}{{\epsilon }^2}$ 时，利用泰勒展开及欧拉公式从另一个角度把永年项(secular terms)化到整体的方程中，避免了永年项的存在。

我们利用四阶龙格库塔算法 [9] 作为参照组，比较以上两种方法在同样条件下的优势。

编写四阶龙格库塔算法时发现步长 $h_{RK}\le \epsilon$ 时，四阶龙格库塔图像才会变得光滑具有周期性，可以很好的用来参照；所以在对比三个算法时要注意多尺度法步长h和四阶龙格库塔算法 $h_{RK}$ 的取值，避免出现参照图像不符，导致最后对比出的结论不正确。

下图2~4都满足：当 $t\in \left[0:100\right]$ ，令 $\epsilon =0.1$ ，对应 $A\left(0\right)=0.1633$ 。

$h=0.01$ (这里h是Multiscale Methods和Reductive Multiscale Methods的步长)。

满足四阶龙格库塔算法步长 $h_{RK}\le \epsilon$ ，这里取0.01。

Figure 2. Amplitude y of fourth orders Runge Kutta and simplified Multiscale Method

图2. 四阶龙格库塔和简化多尺度法的振幅y

图2是四阶龙格库塔和简化多尺度法的振幅y：当黑线为简化多尺度法(Reductive Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅。

Figure 3. Amplitude y of fourth order Runge Kutta and Multiscale Method

图3. 四阶龙格库塔和多尺度法的振幅y

图3是四阶龙格库塔和多尺度法的振幅y：蓝线为多尺度法(Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅。

图4是四阶龙格库塔和多尺度法的振幅y：黑线为简化多尺度法(Reductive Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅；蓝线为多尺度法(Multiscale Methods)的振幅。

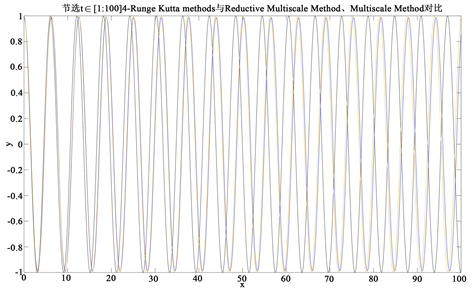
Figure 4. Amplitude y of fourth order Runge Kutta and simplified Multiscale Method and Multiscale Method

图4. 四阶龙格库塔和简化多尺度法、多尺度法的振幅y

由图2~4发现在当 $t\in \left[0:100\right]$ ， $\epsilon =0.1$ ， $h=0.01$ ， $h_{RK}=0.01$ ，时间尺度 $t\le \frac{1}{{\epsilon }^{-2}}$ 时：多尺度法(Multiscale Methods)的振幅图像明显更拟合对照的四阶龙格库塔法的振幅图像，但是还是不够高度拟合；简化多尺度法(Multiscale Methods)的振幅图像明显与对照的四阶龙格库塔法的振幅图像有较大误差；相比较多尺度法而言，在小参数 $\epsilon$ 取值较大时，简化多尺度法误差更大。

下图5~7都满足：当 $t\in \left[0:100\right]$ ，令 $\epsilon =0.01$ ，对应 $A\left(0\right)=0.0516$ 。

$h=0.01$ (这里h是Multiscale Methods和Reductive Multiscale Methods的步长)。

满足四阶龙格库塔算法步长 $h_{RK}\le \epsilon$ ，这里取0.01。

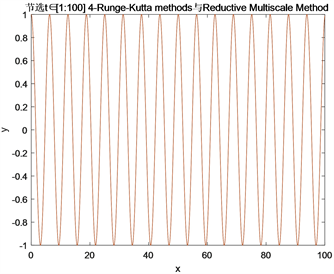
Figure 5. Amplitude y of fourth order Runge Kutta and simplified Multiscale Method

图5. 四阶龙格库塔和简化多尺度法的振幅y

图4是四阶龙格库塔和简化多尺度法的振幅y：当黑线为简化多尺度法(Reductive Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅。

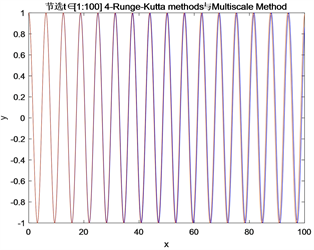
Figure 6. Amplitude y of fourth order Runge Kutta and Multiscale Method

图6. 四阶龙格库塔和多尺度法的振幅y

图6是四阶龙格库塔和多尺度法的振幅y：蓝线为多尺度法(Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅。

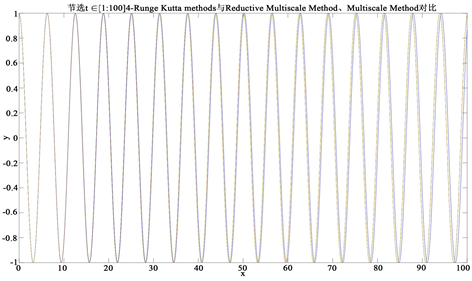
Figure 7. Amplitude y of fourth order Runge Kutta and simplified Multiscale Method and Multiscale Method

图7. 四阶龙格库塔和简化多尺度法、多尺度法的振幅y

图7是四阶龙格库塔和多尺度法的振幅y：黑线为简化多尺度法(Reductive Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅；蓝线为多尺度法(Multiscale Methods)的振幅。

由图5~7发现在当 $t\in \left[0:100\right]$ ， $\epsilon =0.1$ ， $h=0.01$ ， $h_{RK}=0.01$ ，时间尺度 $t\le \frac{1}{{\epsilon }^{-2}}$ 时：当小参数 $\epsilon$ 取值变小时，简化多尺度法(Multiscale Methods)在整个时间尺度t区间上的振幅图像明显更拟合对照的四阶龙格库塔法的振幅图像，有高度拟合的趋势；而多尺度法(Multiscale Methods)的振幅图像明显与对照的四阶龙格库塔法的振幅图像有较小误差，尤其是在时间尺度t区间取50 ( $t<\frac{1}{{\epsilon }^{-1}}$ )之后。总结来说，简化多尺度法(Multiscale Methods)在小参数 $\epsilon$ 取值变小时的图像相比较于多尺度法，振幅图像更加拟合参照振幅图像，具有很大的优势；其次简化多尺度法(Multiscale Methods)和多尺度法(Multiscale Methods)的振幅图像变得更加拟合起来，侧面验证了简化多尺度法(Multiscale Methods)的稳定性。

下图8~10都满足：当 $t\in \left[0:100\right]$ ，令 $\epsilon =0.001$ ，对应 $A\left(0\right)=0.0\text{163}$ 。

$h=0.001$ (这里h是Multiscale Methods和Reductive Multiscale Methods的步长)。

满足四阶龙格库塔算法步长 $h_{RK}\le \epsilon$ ，这里取0.001。

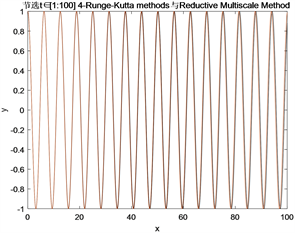
Figure 8. Amplitude y of fourth-order Runge Kutta and simplified Multiscale Method

图8. 四阶龙格库塔和简化多尺度法的振幅y

图8是四阶龙格库塔和简化多尺度法的振幅y：当黑线为简化多尺度法(Reductive Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅。

Figure 9. Amplitude y of fourth-order Runge Kutta and Multiscale Method

图9. 四阶龙格库塔和多尺度法的振幅y

图9是四阶龙格库塔和多尺度法的振幅y：蓝线为多尺度法(Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅。

Figure 10. Amplitude y of fourth order Runge Kutta and simplified Multiscale Method and Multiscale Method

图10. 四阶龙格库塔和简化多尺度法、多尺度法的振幅y

图10是四阶龙格库塔和多尺度法的振幅y：黑线为简化多尺度法(Reductive Multiscale Methods)的振幅，红线为四阶龙格库塔法的振幅；蓝线为多尺度法(Multiscale Methods)的振幅。

由图8~10发现在当 $t\in \left[0:100\right]$ ， $\epsilon =0.001$ ， $h=0.001$ ， $h_{RK}=0.001$ ，时间尺度 $t\le \frac{1}{{\epsilon }^{-2}}$ 时：当小参数 $\epsilon$ 取值变得更小时，简化多尺度法(Multiscale Methods)和多尺度法(Multiscale Methods)的振幅图像变得更加高度拟合，其次两种算法在整个时间尺度t区间上的振幅图像明显更拟合对照的四阶龙格库塔法的振幅图像，有高度拟合的趋势；

总结以上所有的图像来说，在其他条件固定，在小参数 $\epsilon$ 取值变得越来越小时，对照四阶龙格库塔法的振幅图像也正面验证了：简化多尺度法(Multiscale Methods)振幅图像和多尺度法(Multiscale Methods)的振幅图像越来越高度拟合，侧面验证了简化多尺度法(Multiscale Methods)的稳定性。

但是从算法推导设计来看，简化多尺度法(Multiscale Methods)按时间尺度选择性展开，相较于多尺度法(Multiscale Methods)按时间尺度全部展开，极大的减少了臃肿的时间尺度方程，从而减少了运算时间，高效稳定地算出了结果。

5. 总结

本文主要介绍了多尺度法的历史和发展背景，并在此基础上提出了一种改进的方法：简化多尺度法，并且以在带小参数的Duffing方程为例，详细而具体地阐述并求解了这两种方法的推导过程和对比实验结果分析。

从而建立起本文的主要思想：首先建立并推导多尺度法和简化多尺度法的主要原理思想和算法程序，其次利用MATLAB编写代码：用大量数据在一定条件固定下，验证改进后的简化多尺度法在求解某些带小参数的非线性微分方程的数值解，并且利用四阶龙哥库塔法对比，得到相对于原始的多尺度法的优势和不足之处。即第三章我们以带小参数的Duffing方程为例，分别固定其中几个重要参数，训练数据并绘制成图，观察其他参数和数值解图像的关系。经过缜密的分析，我们得到了呈现出和我们预期理论推导一致的图像和结果。通过多次实验结果对比，验证了在一定条件下，简化多尺度法计算出的数值解相较于多尺度法的结果，更有优势：即，将臃肿的时间尺度的划分极大地简化，其次利用欧拉公式和泰勒展开的性质将久期项(secular terms)化到尺度方程内部，从而避免了久期项(secular terms)对数值解的影响，使最后得到改进后的简化多尺度法具有精度更高，算法的运算量大幅度减小、效率更高的优势。因此在一定条件下，计算某些复杂的、光滑的、带小参数的非线性微分方程我们可以利用简化多尺度法来进行计算，极大地减少了运算量和运算时间，提高了运算结果的精度

本文在一定条件下，在运用了简化多尺度法求解某些光滑的、带小参数的非线性微分方程数值解的问题上考虑了一些问题，如果在更为复杂的不光滑的、带小参数非线性微分方程上，简化多尺度法是否还具有同样大的优势？因此接下来的工作将针对以上问题，在相关方面进行具体而详细的推导和分析研究，探索出简化多尺度法在带小参数的微分方程的使用范围和应用限制。