高寒地区路基回弹模量检测方法的对比研究

Comparative Study on Testing Methods for Subgrade Rebound Modulus in High-Altitude and Cold Regions

摘要: 以久马高速公路工程多年冻土路基区段为研究对象，考虑不同的路基土回弹模量检测方法。分别利用贝克曼梁、承载板测定回弹模量两种试验方法测定路基回弹弯沉值，在基于多年冻土路基土在工程设计阶段将两种回弹模量检测方法进行检测，针对本标段已经固化后的路基表面，对两者差异进行分析，并对代表性的测试模量值比较，进行回归换算与对比分析，为供设计与施工参考。

Abstract: Taking the permafrost subgrade section of the Jiuma Expressway project as the research object, different methods for detecting the rebound modulus of subgrade soil are considered. Two testing methods, the Beckman beam and bearing plate, were used to determine the rebound modulus of the roadbed. In the engineering design stage based on permafrost roadbed soil, the two rebound modulus testing methods were tested. The differences between the two methods were analyzed for the solidified roadbed surface of this section, and representative test modulus values were compared for regression conversion and comparative analysis, providing a reference for design and construction.

1. 概述

路基作为路面结构的基础，其稳定性与耐久性决定路面的使用寿命。目前，道路工程中用回弹模量表征路基的强度和变形能力，它是指导路基路面厚度设计与施工质量控制的重要指标之一，准确测试回弹模量对路基质量进行评价非常重要。本研究将基于四川省久马高速公路建设，该项目全长219 km，本工程多标段的路基土处于冻土区域，在土壤含水量、冻结温度、湿度、土壤含水量等条件的影响下，会出现非均匀冻胀现象，造成路基裂缝的主要原因是在春季气温上升后路基冻结层开始融化，如果不能及时排除水分，路基土体将趋于饱和，土粒间的作用力会下降甚至消失，在外部载荷的作用下形成路基下沉、翻浆冒泥等问题，严重影响道路的使用寿命和稳定性 [1] [2] 。须依据设计要求检测出该路段的路基准确的回弹模量值。路基作为路面结构的基础，其稳定性与耐久性决定路面的使用质量。当下的研究表明，公路工程中常用回弹模量来衡量路基的强度和变形能力。路基路面厚度是指导路基路面设计和施工质量控制的重要指标之一 [3] [4] [5] 。回弹模量的准确测定对评价路基质量具有重要意义。考虑会存在不同标段所采用的方法不同的情况，采用了不同的路基土回弹模量检测方法。

基于此，本次研究选取了两个具有代表性的标段，分别利用贝克曼梁、承载板测定回弹模量两种试验方法测定路基回弹弯沉值，在基于多年冻土路基土在工程设计阶段将两种回弹模量检测方法进行检测，承载板法和贝克曼梁法的测定路基土的模量所采用的原理是较为类似的 [6] 。考虑高寒地区路基土性质特殊，基于不同方式回弹模量测试方法的研究将很有必要，尤其是针对本标段已经固化后的路基表面，两者是否存在较大的差异，需要对其测试模量值比较，进行回归换算与对比分析，可为设计提供良好的支撑。

2. 贝克曼梁回弹弯沉试验计算回弹模量值

2.1. 试验方法

贝克曼梁弯沉测量仪，梁的端头穿过测定车后轴双轮轮隙，放在车轮前方约10 cm的路面测量点上 [7] 。在最后三点处，横梁通过支点支撑在基座上。在梁的另一部分设置千分表，以测量端部的上升和下降量。车辆以爬行速度向前移动，当车轮通过末端时，千分表的最大读数被读取；车辆离开后，读取千分表读数；差值的两倍是路面的回弹挠度值L_i。

按下式计算测定值的算术平均值( $\bar{L}$ )、单次测量的标准差(S)和自然误差( $r_0$ )：

$\bar{L}=\frac{{\displaystyle \sum L_i}}{N}$ (1)

$S=\frac{\sqrt{{\displaystyle \sum {\left(L_i-\bar{L}\right)}^2}}}{N-1}$ (2)

$r_0=0.675\times S$ (3)

式中： $\bar{L}$ ——回弹弯沉的平均值(0.01 mm)；

S——回弹弯沉测定值的标准差(0.01 mm)；

r₀——回弹弯沉测定值的自然误差(0.01 mm)；

L_i——各测点的回弹弯沉值(0.01 mm)；

N——测点总数。

计算测量值与每个测量点算术平均值之间的偏差 $d_i=L_i-\bar{L}$ 时，共同计算较大的偏差与自然误差的比值，即d_i/r₀。当某个测点的观测值d_i/r₀的值大于表1的d/r极限值时则应舍弃该测点，然后重复式(1~3)的步骤计算所余各测点的算术平均值( $\bar{L}$ )及标准差(S)。

Table 1. d/r limit values for corresponding different observations

表1. 相应不同观测次数的d/ r极限值

再按下式计算代表弯沉值：

$L_1=\bar{L}+S$ (4)

式中：L₁——计算代表弯沉值；

$\bar{L}$ ——舍弃不合要求的测点后所余各测点弯沉的算术平均值；

S——舍弃不合要求的测点后所余各测点弯沉的标准差。

最后，按下式计算土基的回弹模量(E₀)：

$E_{\text{0}}=\frac{2p\delta }{L_1}\left(1-{\mu }^2\right)a$ (5)

式中：E₀——计算土基的回弹模量(MPa)；

p——测定车轮的平均垂直荷载(MPa)；

δ——测定用标准车双圆荷载单轮传压面当量圆的半径(cm)；

µ——土基的泊松比。一般取为0.35；

a——弯沉系数，为0.712。

2.2. 测点回弹模量值计算整理

贝克曼梁试验法测点所得到的回弹模量值如表2所示。

Table 2. Rebound modulus values of measurement points using Beckman beam test method

表2. 贝克曼梁试验法测点回弹模量值

3. 承载板试验测定回弹模量值

该方法适用于现场的地基基础。将细砂均匀摊铺在已铲平的土基表面，稍微找平，将大承力板放在稳定位置，旋转约半周，然后用水平仪校正，用垂直球检查荷载重心是否与φ30 cm承力板中心对齐。然后放置千斤顶(也要居中)，设置参考桩和参考梁，最后以120˚的角度安装贝克曼梁。安装完成后，以0的荷载将支承板压到靠近土基表面的位置，0.2 MPa。卸载后，计量器设置为零，然后将土壤基础分阶段加载。利用承载板的加载和卸载方法，测量了各荷载作用下地基的回弹变形值。每级加载120分钟后读取沉降值。通过排除有显著偏差的回弹变形异常点，绘制载荷P和回弹变形值L的P~L曲线。如果曲线的初始部分是反向的，则应校正原点。在P~L曲线修正后，根据式(6)计算了各级荷载作用下的地基反弹模量，E_i：

$E_i=\frac{\text{π}D}{4}\cdot \frac{p_i}{L_i}\left(1-{\mu }_0^2\right)$ (6)

式中：E_i——相应于各级荷载下的土基回弹模量值(MPa)；

${\mu }_0$ ——土的泊松比，根据部颁设计规范规定取用；

D——承载板直径30 cm；

P_i ——承载板压力(MPa)；

L_i——相对于荷载P_i时的回弹变形(cm)。

最后，根据线性回归方法，通过等式(7)计算试验结束前的回弹变形值和基于土壤的回弹模量E₀值。

$E_0=\frac{\text{π}D}{4}\cdot \frac{{\displaystyle \sum p_i}}{{\displaystyle \sum L_i}}\left(1-{\mu }_0^2\right)$ (7)

式中：E₀——相应于各级荷载下的土基回弹模量值(MPa)；

${\mu }_0$ ——土的泊松比，土基一般取为0.35；

L_i——结束试验前的各级实测回弹变形值(cm)；

P_i——对应于L_i的各级压力值(MPa)。

大多数P~L曲线略为凸状，少量(土壤干燥且密实时)具有近似线性关系。因此，回弹模量值仍然是一个随荷载压力的增加而减小的变量，应根据路基的实际压力(或回弹弯曲)进行取值。但对于轴承板的测试到底要达到什么目的，目前还没有统一的方法。干、中湿路基应力应变P~L曲线基本呈线性，E₀值变化不大，基本稳定。湿、过湿土地基的应力应变P~L曲线和E₀值随变形量的增加而减小。对于高速、一级和二级公路的半刚性基层，由于路基较厚，模量较高，因此根据多年冻土路基进入到春夏溶解期的实际情况 [8] ，以总变形达到1 mm标志试验结束。

将测点回弹模量值原点修正图和数据计算整理，如图1所示。

Figure 1. Origin correction diagram of rebound modulus value

图1. 修正原点示意图

4. 对比和分析

根据工程实践可知，当软弱土层承载力不足时，采用多年冻土固化的方式可以有效提高地基承载力，但这种方式的离散性较大，因此为了获得更广泛的代表性和数据的准确性，现将检测范围扩大至整个标段，扩大检测面后，试验团队选取了20个检测点后，分别采用贝克曼梁法、承载板法检测现场多年冻土路基的回弹模量值，最终检测结果见图2所示。图中，贝克曼梁法所测回弹模量标记为E₁，承载板法所测回弹模量标记为E₀。

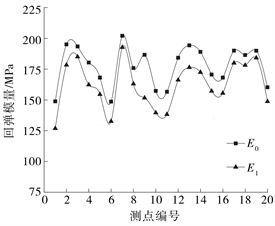
Figure 2. Rebound modulus of roadbed under different detection methods

图2. 不同检测方法下路基回弹模量

从图2可以看出，总体而言贝克曼梁法所测回弹模量值略低于承载板法所测得，从误差分析可以看出，其总体相差值不超过5%，是具有很强的相关性的。数据分析中选取了弯沉L，运用线性、对数和指数的回归模型对两种回弹模量数据E₁和E₀进行模拟，并获取其相关性系数，分析结果如表3所示。

Table 3. Regression models for two types of rebound modulus and deflection values

表3. 两种回弹模量与弯沉值的回归模型

从回归结果可以看出，采用线性和对数的回归模式得到的表达式，使得弯沉和回弹模量具有更好的相关性，其中承载板法的相关性微强于贝克曼梁法。因此在接下来的设计与施工检测过程中，推荐使用。

5. 结论

1) 对于高寒地区的路基回弹模量而言，贝克曼梁试验法与承载板试验法所测值相近，结果相近，贝克曼梁法所测回弹模量值略低于承载板法所测得的回弹模量值，从误差分析可以看出，其总体相差值不超过5%。

2) 在条件恶劣区域，利用贝克曼梁试验法确定土基回弹模量操作相对较易，对于人工操作更为友好，通过数据反算即可得出回弹模量，可提供误差较小的数据。

3) 对于多年冻土路基，贝克曼梁法、承载板法回弹模量变化趋势相近，具有良好的相关性。其中在弯沉和回弹模量的关系中，其关系可通过相关性更强的线性或对数回归模型表示，其中相关性方面承载板法的相关性微强于贝克曼梁法。