含t-积结构的张量广义Krylov子空间方法求解线性离散不适定问题

The Tensor Generalized Krylov Subspace Method with t-Product Structure for Solving Linear Discrete Ill-Posed Problems

摘要: 本文讨论了基于三阶张量的t-积形式，将广义Krylov子空间方法在解决大规模线性离散不适定问题中的应用。针对于离散不适定问题，首先确定正则化参数，并将一系列投影应用到广义的Krylov子空间上。数据张量是一般的三阶张量或由横向定向矩阵定义的张量。在数值例子和彩色图像修复中的应用说明了该方法的有效性。

Abstract: This article discusses the application of the generalized Krylov subspace method in solving large-scale linear discrete ill-posed problems based on the t-product form of third-order tensors. For discrete ill-posed problems, the regularization parameters are first determined, and a series of projections are applied to the generalized Krylov subspace. A data tensor is a general third-order tensor or a tensor defined by a transversely oriented matrix. The application of this method in nu-merical examples and color image restoration demonstrates its effectiveness.

1. 引言

具有张量形式的线性离散不适定问题是彩色图像复原、视频去模糊、目标识别、层析成像图像重建等领域的共性问题，是数值代数的一个重要研究内容之一。许多图像恢复方法通过叠加表示图像的矩阵元素来对每个图像进行向量化。矩阵条目表示编码灰度值的像素值。每一帧表示一个图像，因此，一个视频可以被表示为一个长向量，每个条目表示某一帧中的一个像素值。然而，这种表示破坏了原始视频帧可能拥有的空间相关性和结构复杂性。具有t-积结构的三阶张量系统由Kilmer等人 [1] 提出，该系统避免了矩阵化和向量化，保留了多维结构。t-乘积已被证明有用的应用领域包括面部识别 [2] 、层析图像重建 [3] 、视频补全 [4] 和图像分类 [5] 。用t-积求解大规模离散线性不适定问题的方法有很多。Kilmer等人 [2] 提出了一种张量共轭梯度(t-CG)方法以求解张量线性系统 $\mathcal{A}\ast \stackrel{\to }{\mathcal{X}}=\stackrel{\to }{\mathcal{B}}$ 的最小二乘问题。Zhang等人 [6] 提出了计算超大数据集的随机张量奇异值分解(rtSVD)方法，在图像数据压缩和分析方面具有应用前景。Ugwu和Reichel [7] 提出了一种新的随机张量奇异值分解(R-tSVD)，该方法改进了 [1] 中的截断张量奇异值分解(T-tSVD)。Guide等人 [8] 开发了张量T-全局GMRES算法和张量T-全局Golub-Kahan算法，并使用季洪诺夫正则化技术获得了有效的正则化解。最近，Reichel等人引入了张量Golub-Kahan双对角化方法 [9] 、张量Arnoldi-Tikhonov和张量GMRES-type [10] ，通过将大尺度问题简化为小尺度问题来解决大规模线性不适定问题。Lampe等人 [11] 开发了广义Krylov子空间(GKS)方法来求解大规模Tikhonov正则化问题。

2. 预备知识

对于三阶张量 $\mathcal{A}\in {ℝ}^{l\times m\times n}$ ，图1显示了正面切片 ${\mathcal{A}}_{\left(:,:,k\right)}$ 、横向切片 ${\mathcal{A}}_{\left(:,j,:\right)}$ 和管 ${\mathcal{A}}_{\left(i,j,:\right)}$ 。为了简化，我们缩写为 $A_k={\mathcal{A}}_{\left(:,:,k\right)}$ 。在t-积的定义中广泛地使用循环矩阵

$v={\left[\begin{array}{cccc}{v}_0& v_1& v_2& v_3\end{array}\right]}^{\text{T}}$ ，

则

$\text{circ}\left(v\right)=\left[\begin{array}{cccc}{v}_0& v_3& v_2& v_1\\ v_1& v_0& v_3& v_2\\ v_2& v_1& v_0& v_3\\ v_3& v_2& v_1& v_0\end{array}\right]$

是一个循环矩阵。循环矩阵可以用归一化离散傅里叶变换(DFT)矩阵，它是酉矩阵。特别地，如果v是 $n\times 1$ ， $F_n$ 是 $n\times n$ DFT矩阵， $F_n^{\ast }$ 是它的共轭转置，则

$F_n\text{circ}\left(v\right)F_n$

是对角的。从一个张量的切片中创建一个块循环矩阵。假设块循环是由张量正面切片创建的，我们利用上面的例子得到块–循环矩阵

$\text{bcirc}\left(\mathcal{A}\right)=\left[\begin{array}{ccccc}{A}_1& A_n& A_{n-1}& \cdots & A_2\\ A_2& A_1& A_n& \cdots & A_3\\ ⋮& ⋮& \ddots & \ddots & ⋮\\ A_n& A_{n-1}& \cdots & A_2& A_1\end{array}\right]$ .

一个 $ln\times m$ 矩阵由 $\text{unfold}\left(\mathcal{A}\right)$ 得到，而算子fold将这个矩阵折叠回张量 $\mathcal{A}$ ，即，

$\text{unfold}\left(\mathcal{A}\right)=\left[\begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_n\end{array}\right],\text{fold}\left(\text{unfold}\left(\mathcal{A}\right)\right)=\mathcal{A}.$

定义 给定两个张量 $\mathcal{A}\in {ℝ}^{l\times m\times n}$ 和 $\mathcal{B}\in {ℝ}^{m\times p\times n}$ ，它们之间的t-积 $\mathcal{A}\ast \mathcal{B}$ 被定义为

$\mathcal{A}\ast \mathcal{B}=\text{fold}\left(\text{bcirc}\left(\mathcal{A}\right)\text{unfold}\left(\mathcal{B}\right)\right)=\mathcal{C},$

这里 $\mathcal{C}\in {ℝ}^{l\times p\times n}$ 。

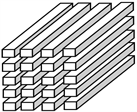
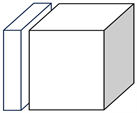
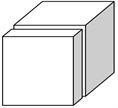(a) (b) (c)

Figure 1. (a) Frontal slices ${\mathcal{A}}_{\left(:,:,k\right)}$ ; (b) Lateral slices ${\mathcal{A}}_{\left(:,j,:\right)}$ ; (c) Tube fibers ${\mathcal{A}}_{\left(i,j,:\right)}$

图1. (a) 正面切片 ${\mathcal{A}}_{\left(:,:,k\right)}$ ；(b) 横向切片 ${\mathcal{A}}_{\left(:,j,:\right)}$ ；(c) 管 ${\mathcal{A}}_{\left(i,j,:\right)}$

张量QR(tQR)的分解由Kilmer等人 [12] 描述。 $\mathcal{A}\in {ℝ}^{l\times m\times n}$ 的QR分解表示为

$\mathcal{A}=\mathcal{Q}\ast \mathcal{R},$

其中张量 $\mathcal{Q}\in {ℝ}^{l\times m\times n}$ 是部分正交的， $\mathcal{R}\in {ℝ}^{m\times m\times n}$ 的每个正面切片是一个上三角形。算法1的tQR分解是在傅里叶域实现tQR分解。

算法1. tQR分解 [1]

表1是本文所使用的符号的说明，

Table 1. Symbol description

表1. 符号说明

3. 张量Tikhonov正则化方法

本文旨在求解张量t-积结构的线性系统

$\mathcal{A}\ast \stackrel{\to }{\mathcal{X}}=\stackrel{\to }{\mathcal{B}},\mathcal{A}={\left[a\right]}_{i,j,k=1}^{l,m,n}\in {ℝ}^{l\times m\times n},\stackrel{\to }{\mathcal{B}}\in {ℝ}^{l\times 1\times n},l\ge m,$ (3.1)

和最小二乘问题

$\underset{\stackrel{\to }{\mathcal{X}}\in {ℝ}^{m\times 1\times n}}{\min }{\Vert \mathcal{A}\ast \stackrel{\to }{\mathcal{X}}-\stackrel{\to }{\mathcal{B}}\Vert }_F^2.$ (3.2)

张量 $\mathcal{A}$ 的管秩的确定不明，即很难有意义地定义 $\mathcal{A}$ 的管秩。具体地说， $\mathcal{A}$ 的奇异管的Frobenius范数随指数数的增加而迅速衰减为零。特别地，它的许多奇异管以不同数量级的微小Frobenius范数的形式存在，使得最小化变得离散不适定，此时称问题(3.1)为张量离散线性不适定问题。它们产生于彩色图像和视频的恢复，如 [1] [9] [10] 。

一般情况下，不适定问题(3.1)的右端张量列 $\stackrel{\to }{\mathcal{B}}$ 是观察得到的数据，假设 ${\stackrel{\to }{\mathcal{B}}}_{ture}$ 是一个未知的、不可用的张量列，则真实解对应的线性方程为 $\mathcal{A}\ast {\stackrel{\to }{\mathcal{X}}}_{ture}={\stackrel{\to }{\mathcal{B}}}_{ture}$ ，在问题(3.1)中， ${\stackrel{\to }{\mathcal{B}}}_{ture}$ 被噪声 $\stackrel{\to }{\mathcal{E}}\in {ℝ}^{m\times 1\times n}$ 污染，即，

$\stackrel{\to }{\mathcal{B}}={\stackrel{\to }{\mathcal{B}}}_{true}+\stackrel{\to }{\mathcal{E}}.$

由于 $\mathcal{A}$ 的某些正面切片的条件数很大以及 $\stackrel{\to }{\mathcal{B}}$ 中噪声 $\stackrel{\to }{\mathcal{E}}$ 的影响，它的直接解是没有意义的。正则化通常是用来减少(3.1)的病态性的影响。我们考虑Tikhonov正则化，并替换问题(3.1)为张量惩罚最小二乘问题

$\underset{\stackrel{\to }{\mathcal{X}}\in {ℝ}^{m\times 1\times n}}{\text{arg}\min }\left\{{\Vert \mathcal{A}\ast \stackrel{\to }{\mathcal{X}}-\stackrel{\to }{\mathcal{B}}\Vert }_F^2+\mu {\Vert \mathcal{X}\Vert }_F^2\right\},$ (3.3)

这里的 $\mu >0$ 为正则化参数。最小化问题(3.3)的正规方程为

$\left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}+\mu \mathcal{I}\right)\ast \stackrel{\to }{\mathcal{X}}={\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}.$ (3.4)

4. 张量广义Krylov子空间方法

本文将矩阵形式的广义Krylov子空间(GKS)方法推广到具有t-积结构的三阶张量系统中，得到了张量广义Krylov子空间投影方法(tGKS)。考虑了tGKS方法来构造(3.4)的子空间。我们在解空间中构造了一组基 ${\mathcal{V}}_k\in {ℝ}^{m\times k\times n}$ ，用张量列 ${\stackrel{\to }{\mathcal{V}}}_j\in {ℝ}^{m\times 1\times n}$ 表示为

${\mathcal{V}}_k=\left[{\stackrel{\to }{\mathcal{V}}}_1,{\stackrel{\to }{\mathcal{V}}}_2,\cdots ,{\stackrel{\to }{\mathcal{V}}}_k\right].$

定理 假设在t-积结构中， $\mathcal{N}\left(\mathcal{A}\right)$ 表示张量 $\mathcal{A}$ 的零空间，当问题(3.3)满足 $\mathcal{N}\left(\mathcal{A}\right)\cap \mathcal{N}\left(\mathcal{I}\right)=\stackrel{\to }{\mathcal{O}},$

且 $\mu >0$ ，最小化问题(3.3)有一个唯一的解

${\stackrel{\to }{\mathcal{X}}}_{\mu }={\left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}+\mu \mathcal{I}\right)}^{-1}\ast {\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}.$

定理证明详见文献 [9] 。使 $\stackrel{\to }{\mathcal{X}}={\mathcal{V}}_k\ast \stackrel{\to }{\mathcal{Y}}\left(k\ll n\right)$ ，则可获得(3.3)的变体

$\underset{\stackrel{\to }{\mathcal{Y}}\in {ℝ}^{k\times 1\times n}}{\arg \min }\left\{{\Vert \mathcal{A}\ast {\mathcal{V}}_k\ast \stackrel{\to }{\mathcal{Y}}-\stackrel{\to }{\mathcal{B}}\Vert }_F^2+{\mu }^{-1}{\Vert {\mathcal{V}}_k\ast \stackrel{\to }{\mathcal{Y}}\Vert }_F^2\right\}$ . (4.1)

${\mathcal{V}}_k$ 是张量列正交的，且满足 ${\mathcal{V}}_k^{\text{T}}\ast {\mathcal{V}}_k=\mathcal{I}$ ，正规方程(3.4)到子空间 ${\mathcal{V}}_k$ 中的投影可以表示为

${\mathcal{V}}_k^{\text{T}}\ast \left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}+{\mu }^{-1}\mathcal{I}\right)\ast {\mathcal{V}}_k\ast {\stackrel{\to }{\mathcal{Y}}}_{\mu }={\mathcal{V}}_k^{\text{T}}\ast {\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}.$ (4.2)

将 $\mu >0$ 设置为一个可用的正则化参数，可以得到

${\stackrel{\to }{\mathcal{Y}}}_{\mu }={\left({\mathcal{V}}_k^{\text{T}}\ast \left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}+{\mu }^{-1}\mathcal{I}\right)\ast {\mathcal{V}}_k\right)}^{-1}\ast {\mathcal{V}}_k^{\text{T}}\ast {\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}.$ (4.3)

直接计算(4.3)的代价是昂贵的，由于张量 $\mathcal{A}$ 的数据量过大，整体计算 ${\mathcal{V}}_k^{\text{T}}\ast \left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}+{\mu }^{-1}\mathcal{I}\right)\ast {\mathcal{V}}_k$ 的t-积的逆会占据过多内存，一种合理的考虑是将 $\mathcal{A}\ast {\mathcal{V}}_k$ 进行分解，可使用张量QR(tQR)分解。即使得

$\mathcal{A}\ast {\mathcal{V}}_k={\mathcal{Q}}_A\ast {\mathcal{R}}_A,$

则可得到

$\left({\mathcal{R}}_A^{\text{T}}\ast {\mathcal{R}}_A+{\mu }^{-1}{\mathcal{V}}_k^{\text{T}}\ast {\mathcal{V}}_k\right)\stackrel{\to }{\mathcal{Y}}={\mathcal{R}}_A^{\text{T}}\ast {\mathcal{Q}}_A^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}.$ (4.4)

对于(4.4)的解并结合 $\stackrel{\to }{\mathcal{X}}={\mathcal{V}}_k\ast \stackrel{\to }{\mathcal{Y}}$ ，获得(3.4)的残差

${\mathcal{R}}_k=\left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}+{\mu }^{-1}\mathcal{I}\right)\ast {\mathcal{V}}_k\ast {\stackrel{\to }{\mathcal{Y}}}_k-{\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}.$ (4.5)

在更新搜索空间 ${\mathcal{V}}_k$ 过程中，不可避免地会出现一个舍入错误。为了增强正交性，将 ${\mathcal{R}}_k$ 重新正交化用于更新 ${\mathcal{V}}_k$ 。因此

${\bar{\mathcal{R}}}_k=\left(\mathcal{I}-{\mathcal{V}}_k\ast {\mathcal{V}}_k^{\text{T}}\right)\ast {\mathcal{R}}_k,\left[{\stackrel{\to }{\mathcal{V}}}_{k+1},~\right]=\text{Normalize}\left({\bar{\mathcal{R}}}_k\right),{\mathcal{V}}_{k+1}=\left[{\mathcal{V}}_k,{\stackrel{\to }{\mathcal{V}}}_{k+1}\right].$ (4.6)

方程(3.1)为标准形式， ${\mathcal{V}}_k$ 的张量列构成k维张量Krylov子空间的标准正交基 ${\mathcal{K}}_{k+1}\left({\mathcal{A}}^{\text{T}}\ast \mathcal{A},{\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}\right)=span\left\{{\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}},\left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}\right)\ast {\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}},\cdots ,{\left({\mathcal{A}}^{\text{T}}\ast \mathcal{A}\right)}^k\ast {\mathcal{A}}^{\text{T}}\ast \stackrel{\to }{\mathcal{B}}\right\}.$

综合(3.1)~(4.6)，得到了算法2的张量广义Krylov子空间-Tikhonov方法(tGKS-T)。

算法2. tGKS-T

5. 数值列子

本节说明了当应用于解决线性离散不适定问题时所描述的方法的性能。本节所有的计算都是在intel core i7和16GB ram的电脑上使用MATLAB 2018进行的。

设 ${\mathcal{X}}_k$ 方法是用所选方法对最小化问题(3.1)的计算解。为了比较计算解的质量，我们评估了相对误差

$E_k=\frac{{\Vert {\mathcal{X}}_k-{\mathcal{X}}_{true}\Vert }_F}{{\Vert {\mathcal{X}}_{true}\Vert }_F},$

以及信噪比

$SNR\left({\mathcal{X}}_k\right)=10{\log }_{10}\frac{{\Vert {\mathcal{X}}_{true}-E\left({\mathcal{X}}_{true}\right)\Vert }_F^2}{{\Vert {\mathcal{X}}_k-{\mathcal{X}}_{true}\Vert }_F^2},$

对于由三阶张量 $\stackrel{\to }{\mathcal{B}}$ 给出的数据的问题的相对误差被类似地确定。

在数值实验中，我们同样考虑作为彩色图像和视频恢复的实验，将三通道的彩色图像通过squeeze和twist算子 [2] 进行与侧向切片的转换，可将三通道彩色图像的恢复问题分解为p个问题(3.1)，我们将三通道彩色图像和视频恢复问题描述为

$\underset{\mathcal{X}\in {ℝ}^{m\times p\times n}}{\min }\left\{{\Vert \mathcal{A}\ast \mathcal{X}-\mathcal{B}\Vert }_F^2+\mu {\Vert \mathcal{X}\Vert }_F^2\right\},$

其中生成一个“噪声”张量 $\mathcal{E}$ ，通过确定横向切片 ${\stackrel{\to }{\mathcal{E}}}_j,j=1,2\text{,}\cdots$ ，模拟数据张量 $\mathcal{B}={\mathcal{B}}_{true}+\mathcal{E}$ 的误差。它们的项以零均值正态分布，并被缩放以对应一个特定的噪声水平 $$ 。因此

${\stackrel{\to }{\mathcal{E}}}_j=\nu \frac{{\stackrel{\to }{\mathcal{E}}}_{r,j}}{{\Vert {\mathcal{E}}_{r,j}\Vert }_F}{\Vert {\mathcal{B}}_{true,j}\Vert }_F,j=1,\cdots ,p,$

其中， ${\stackrel{\to }{\mathcal{E}}}_{r,j}$ 的条目按N(0, 1)分布。

例子5.1 数值恢复

取矩阵 $A_1=baart\left(400\right)$ 由Hansen的正则化工具 [13] 中的函数baart生成，并在MATLAB中定义 $A_2=gallery\left(\text{'}prolate\text{'},400,\alpha \right)$ 。我们取α = 0.50。那么 $A_2$ 是一个对称的正定病态的Toeplitz矩阵。在此，可以定义 $\mathcal{A}$ 为

${\mathcal{A}}_{\left(:,:,i\right)}=A_1\left(i,1\right)A_2.$

确切的数据张量 ${\stackrel{\to }{\mathcal{B}}}_{true}\in {ℝ}^{400\times 1\times 400}$ 由 $\mathcal{A}\ast {\stackrel{\to }{\mathcal{X}}}_{true}={\stackrel{\to }{\mathcal{B}}}_{true}$ 得到，而精确数据 ${\stackrel{\to }{\mathcal{X}}}_{true}\in {ℝ}^{400\times 1\times 400}$ 的所有元素均为1。生成了受噪声污染的数据张量由 $\mathcal{B}={\mathcal{B}}_{true}+\mathcal{E}$ 产生，而张量 $\mathcal{A}$ 的每个正面切片 ${\mathcal{A}}_{\left(:,:,k\right)}$ 的条件数都满足 $cond\left({\mathcal{A}}_{\left(:,:,k\right)}\right)>{10}^7$ 。本文设定的噪音水平在实际计算中设为不可知，正则化参数通过多次实验得到一个合理值，有关正则化参数可以通过L-曲线，差异原理等方式确定，而正则化参数的合理设定以及求解已远远超出本文范围，本文不再讨论。

表2给出了在不同噪声水平下由tGKS方法和一般矩阵系统的广义Krylov子空间方法(GKS)计算出的信噪比和相对误差，所需的迭代次数(子空间维数k)，以及计算时间。表中的数据显示tGKS方法的恢复效果优于GKS。tGKS方法使用了比GKS更多的时间，但tGKS只需要构造少数的子空间，且得到的解的相对误差 $E_k$ 与SNR都优于GKS，这是由于tGKS的张量t-积结构可以整体考虑数据。

Table 2. Result of example 5.1

表2. 例子5.1结果

例子5.2 彩色图像恢复

此示例显示了模糊彩色图像Lena在tGKS方法下的恢复情况。在MATLAB中原始图像数据存储为张量 ${\stackrel{\to }{\mathcal{X}}}_{ori}\in {ℝ}^{256\times 256\times 3}$ ，并将这个张量转换为张量 ${\stackrel{\to }{\mathcal{X}}}_{true}\in {ℝ}^{256\times 3\times 256}$ ，设置 $N=256,\sigma =3$ 和band = 12，定义 $\mathcal{A}\in {ℝ}^{256\times 256\times 256}$ ，其中 $cond\left({\mathcal{A}}_{\left(:,:,k\right)}\right)>{10}^8$ ， $k\le 12$ ，即，

$\begin{array}{l}z=\left[exp\left(-\left({\left[0:band-1\right]}^2\right)/\left(2{\sigma }^2\right)\right),zeros\left(1,N-band\right)\right],\\ A=toeplitz\left(z\right),{\mathcal{A}}_{\left(:,:,i\right)}=\frac{1}{2\pi \sigma }A\left(i,1\right)A,i=1,\cdots ,256.\end{array}$

Table 3. Result of Example 5.2

表3. 例子5.2结果

表3显示了例子5.2的在不同噪音水平下的结果，在噪音水平较小时，所需要的迭代时间更多，这是由于在更小的噪音水平的系统中进行迭代时，要达到设置的收敛条件需要更多次迭代，可以得到更精确的迭代解，因此当满足设置的算法停止标准时，更小的噪音水平的系统的迭代时间虽然更长，但得到的解更精确。

矩阵系统的GKS方法在MATLAB上进行彩色图像的恢复实验中，通常是将彩色图像三通道进行矩阵平展开后进行矢量化，这样的方式意味着要建立更多的子空间。

而tGKS方法的张量t-积考虑了彩色图像三通道之间可能存在的空间结构性，从整体上对模糊和加噪的彩色图像进行恢复，建立了比GKS方法少的子空间，恢复效果也优于GKS方法。

图2给出了彩色图像Lena和被模糊加了噪音的图像，以及tGKS方法和GKS方法下的恢复图像。

Figure 2. The restoration effect of color images in Table 3 with $\delta ={10}^{-3}$

图2. 表3中 $\delta ={10}^{-3}$ 时，彩色图像的恢复效果图

6. 结论

相对于传统方法，即将模糊图像进行矩阵化或者向量化，张量t-积结构考虑了各个通道间的空间结构性。本文介绍的含t-积结构的张量广义Krylov子空间方法在求解离散不适定问题时，建立的Krylov子空间维数较少，通过说明例证明了所提出的方法在数值计算和图像恢复应用中的有效性。值得注意的是，tGKS方法通过相对误差和信噪比值评估，提供了图像恢复算法性能的综合评估，在图像恢复和视频恢复上显示出显著的潜力。

基金项目

四川省中央引导地方科技发展专项项目(2022ZYD0008)。