Cholesky分解的单Pass随机算法

Single-Pass Randomized Algorithm for Cholesky Decomposition

摘要: 对于大规模数据矩阵，数据的读取成本远高于算法本身的成本；对存储在磁盘外部的流型数据，往往只有一次读取数据的机会。而以往的Cholesky分解的随机算法都至少需要读取输入数据两次，难以满足实际应用中的低成本需求。本文基于矩阵分解的单pass随机算法研究，提出了Cholesky分解的单pass随机算法，并给出了该算法的误差上界，最后通过数值实验验证了该算法的可行性以及有效性。

Abstract: For large-scale data matrices, the cost of data reading is much higher than the cost of algorithms. For streaming data stored outside the disk, there is only one chance to read the data. In the past, the randomized algorithm of Cholesky decomposition needed to read the original data at least twice, which was difficult to meet the low-cost requirements in practical applications. Based on the research of single-pass randomized algorithm with matrix decomposition, a single-pass randomized algorithm based on Cholesky decomposition is proposed, and the error upper bound of the algorithm is given, and finally the feasibility and effectiveness of the algorithm are verified by numerical experiments.

1. 问题的提出

矩阵Cholesky分解的算法是数值线性代数的一个重要内容，其在最小二乘、线性回归、非线性优化等科学计算问题中具有广泛的应用。Cholesky分解 [1] 源于矩阵的LU分解，即对对称正定矩阵 $A\in R^{m\times m}$ ，存在唯一的对角元素皆为正的下三角矩阵 $L\in R^{m\times m}$ ，使得A可以分解为 $A=L{L}^{\text{T}}$ 。为了增强数值稳定性，2002年，Hammarling [2] 提出了全主元的Cholesky分解。2004年，Gu和Miranian [3] 又提出了Cholesky分解的秩显算法。2016年，Xiao和Gu [4] 提出了Cholesky分解在分块形式下的低秩逼近算法，进一步给出了谱显分解算法，从而使得算法变得高效稳定。然而，这些确定性算法在矩阵的低秩逼近分解中时间成本过高，导致算法的效率较低。为了改进这些不足，文献 [5] 提出的主元随机Cholesky分解算法不仅有很好的低秩逼近效果，而且节省了大量时间成本。

但是这类随机算法的通病都是至少需要读取输入矩阵两次。而面对存储在内存外部的大规模数据和流型数据时，往往只有一次读取数据的机会。于是就有学者提出将单pass随机算法应用到矩阵分解的低秩逼近随机算法中。2011年，Halko和Martinsson等 [6] 首次提出了将单pass随机算法应用到矩阵的特征值分解，而后Tropp和Yurtsever等 [7] [8] 提出了一种新的SVD分解的单pass随机算法。接着，在2020年Li和Yin [5] 提出了LU分解的单pass随机算法。在此基础上，本文从随机矩阵投影的角度构造了一种新的随机算法——Cholesky分解的单pass随机算法，并给出了相应的误差上界。同时通过数值实验对Cholesky分解的几种算法进行了比较。

2. 预备知识

定义1 [9] 设 $\mu \ge 1$ ， $a_1>0$ ， $a_2>0$ ，亚高斯随机矩阵 $\mathcal{A}\left(\mu ,a_1,a_2,m,n\right)$ 是一个由所有 $m\times n$ 阶随机矩阵 $A=\left({\xi }_{ij}\right)$ 所构成的矩阵集，A中的元素皆为服从i.i.d.的随机变量，且满足下述三个条件:

1) $E\left({\left|{\xi }_{ij}\right|}^3\right)\le {\mu }^3$ ；

2) $E\left({\xi }_{ij}^2\right)\ge 1$ ；

3) $P\left({\Vert A\Vert }_2>a_1\sqrt{m}\right)\le {\text{e}}^{-a_{2}m}$ 。

注1 从文献 [9] 可知，如果A是 $m\times n\left(m>n\right)$ 阶亚高斯随机矩阵，则有 $A\in \mathcal{A}\left(\mu ,a_1,a_2,m,n\right)$ ，且 $a_1=6\mu \sqrt{a_2+4}$ ，若矩阵 $A_{m\times n}\in \mathcal{N}\left(0,1\right)$ 其中 $m>n$ ，有 $A\in \mathcal{A}\left(\mu ,a_1,a_2,m,n\right)$ ，且 $\mu =\sqrt[3]{\frac{4}{\sqrt{2\pi }}}$ 。

引理1 [9] 若矩阵 $A\in \mathcal{A}\left(\mu ,a_1,a_2,m,n\right)$ ，参数m，n满足 $m>\left(1+\frac{1}{\ln n}\right)n$ ，则存在正常数c₁，c₂使得 $P\left({\sigma }_n<c_1\sqrt{m}\right)\le {\text{e}}^{-c_{2}m}$ 成立。

注2 由文献 [10] ，可知引理1中参数c₁，c₂的确切值：

$c_1=\frac{b}{c^2{c}_3}{\left(\frac{b}{3e^2{c}_3{a}_1}\right)}^{\frac{1}{\delta }}$ , $c_2=\min \left(1,\frac{c^{″}}{2{\mu }^6},a^2\right)-\frac{\ln 3}{m}$ ,

其中， $c_3=4\sqrt{\frac{2}{\pi }}\left(\frac{2{\mu }^9}{a_1^3}+\sqrt{\pi }\right)$ ， $b=\min \left(\frac{1}{4},\frac{c^{\prime }}{5a_1{\mu }^3}\right)$ ， $c^{\prime }={\left(\frac{27}{2^{13}}\right)}^{\frac{1}{2}}$ ， $c^{″}=\frac{27}{2^{11}}$ 。

引理2 [11] 设矩阵 $A\in R^{m\times n}$ 的SVD分解为 $A=U\text{Σ}{V}^{\text{T}}$ ，随机矩阵 $\Omega \in R^{n\times k}$ 列满秩， $A\Omega$ 有thin-QR分解 $A\Omega =QR$ ， $V^{\text{T}}\Omega$ 的分块形式为 $V^{\text{T}}\Omega ={\left({\hat{\Omega }}_1^{\text{T}},{\hat{\Omega }}_2^{\text{T}}\right)}^{\text{T}}$ ，其中 ${\hat{\Omega }}_1\in R^{\left(k-p\right)\times k}$ ， ${\hat{\Omega }}_2\in R^{\left(n-k+p\right)\times k}$ 。设 ${\hat{\Omega }}_1$ 行满秩，r是目标秩且满足 $r\le k$ ， $0\le p\le k-r$ ，则有

${\Vert \left(I-Q{Q}^{\text{T}}\right)A\Vert }_F\le \sqrt{\frac{r{\sigma }_1^2{\sigma }_{k-p+1}^2{\Vert {\hat{\Omega }}_2\Vert }_2^2{\Vert {\hat{\Omega }}_1^{†}\Vert }_2^2}{{\sigma }_{k-p+1}^2{\Vert {\hat{\Omega }}_2\Vert }_2^2{\Vert {\hat{\Omega }}_1^{†}\Vert }_2^2+{\sigma }_1^2}+{\displaystyle \underset{i=r+1}{\overset{n}{\sum }}{\sigma }_i^2}}$

3. Cholesky分解的单Pass随机算法(SPRCH)和误差界

3.1. Cholesky分解的单Pass随机算法

本节基于LU分解的单pass随机算法，介绍了一种新的Cholesky分解的单pass随机算法，与算法1相比，它即保留了在低秩逼近算法中较好的效果，又只需对A访问一次，大大的节约了计算成本。类似于算法1的构造，我们可以给出算法2的具体思想如下：

我们可以根据 $PA{P}^{\text{T}}\approx L_y{L}_y^{†}PA{P}^{\text{T}}{\left(L_y^{†}\right)}^{\text{T}}{\left(L_y\right)}^{\text{T}}$ ，然后考虑将算法1中的 $B=L_y^{†}PA{P}^{\text{T}}{\left(L_y^{†}\right)}^{\text{T}}$ 的A替换掉，我们将等式两边同时左乘 $L_y$ ，右乘 $L_y^{\text{T}}$ 得到：

$L_{y}B{L}_y^{\text{T}}\approx L_y{L}_y^{†}PA{P}^{\text{T}}{\left(L_y^{†}\right)}^{\text{T}}{\left(L_y\right)}^{\text{T}}\approx PA{P}^{\text{T}}$

因此我们得到

$L_{y}B{L}_y^{\text{T}}\approx PA{P}^{\text{T}}$

又因为 $Y_2={\Omega }_1^{\text{T}}{Y}_1$ 将等式两边同时左乘 ${\Omega }_1^{\text{T}}{P}^{\text{T}}$ ，右乘 $P{\Omega }_1$ ，我们得到：

${\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_{y}B{L}_y^{\text{T}}P{\Omega }_1\approx {\Omega }_1^{\text{T}}{Y}_1=Y_2$

然后我们得到B的一个近似值：

$B\approx {\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{Y}_2{\left(L_y^{\text{T}}P{\Omega }_1\right)}^{†}$

因此我们就得到了一个新的算法Cholesky分解的单pass随机算法(SPRCH)

取流型数据 $Y_1\leftarrow A{\Omega }_1$ ， $Y_2\leftarrow {\Omega }_1^{\text{T}}{Y}_1$ ，则可通过以下更新公式计算：

$Y_1\left(i,:\right)\leftarrow A\left(i,:\right){\Omega }_1$ , $Y_{2,i+1}\leftarrow Y_{2,i}+{\Omega }_1^{\text{T}}{Y}_1\left(i,:\right)$ , $i=1,2,3,\cdots ,n$ .

3.2. 误差分析

$\begin{array}{c}{\Vert PA{P}^{\text{T}}-L{L}^{\text{T}}\Vert }_F={\Vert PA{P}^{\text{T}}-L_y{L}_b{L}_b^{\text{T}}{L}_y^{\text{T}}\Vert }_F={\Vert PA{P}^{\text{T}}-L_{y}B{L}_y^{\text{T}}\Vert }_F\\ ={\Vert PA{P}^{\text{T}}-L_y{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{Y}_2{\left(L_y^{\text{T}}P{\Omega }_1\right)}^{†}{L}_y^{\text{T}}\Vert }_F\\ \le {\Vert PA{P}^{\text{T}}-L_y{L}_y^{†}PA{P}^{\text{T}}\Vert }_F+{\Vert L_y{L}_y^{†}PA{P}^{\text{T}}-L_y{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{Y}_2{\left(L_y^{\text{T}}P{\Omega }_1\right)}^{†}{L}_y^{\text{T}}\Vert }_F\\ \le \left(1+{\Vert L_y{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{\Omega }_1^{\text{T}}\Vert }_2\right)\cdot {\Vert \left(I-L_y{L}_y^{†}\right)PA\Vert }_F\end{array}$

接下来估计 ${\Vert L_y{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{\Omega }_1^{\text{T}}\Vert }_2$ 的上界，取特殊的p值0，首先对 $L_y$ 做thin-svd分解 $L_y=\hat{U}\hat{\Sigma }{\hat{V}}^{\text{T}}$ ，其中 $\hat{U}\in R^{n\times r}$ ， $\hat{\Sigma }\in R^{r\times r}$ ， $\hat{V}\in R^{r\times r}$ ，即可得到

$\begin{array}{c}{\Vert L_y{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{\Omega }_1^{\text{T}}\Vert }_2={\Vert \hat{U}\hat{\Sigma }{\hat{V}}^{\text{T}}{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}\hat{U}\hat{\Sigma }{\hat{V}}^{\text{T}}\right)}^{†}{\Omega }_1^{\text{T}}\Vert }_2\\ ={\Vert \hat{U}\hat{\Sigma }{\hat{V}}^{\text{T}}{\left(\hat{\Sigma }{\hat{V}}^{\text{T}}\right)}^{-1}{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}\hat{U}\right)}^{†}{\Omega }_1^{\text{T}}\Vert }_2\end{array}$

由于P是置换矩阵，且 $\hat{U}$ 为列正交矩阵，因此， ${\Omega }_1^{\text{T}}{P}^{\text{T}}\hat{U}$ 是一个Gaussian随机矩阵，由引理1，有

${\Vert {\left({\Omega }_1^{\text{T}}{P}^{\text{T}}\hat{U}\right)}^{†}\Vert }_2=\frac{1}{{\sigma }_r\left({\Omega }_1^{\text{T}}{P}^{\text{T}}\hat{U}\right)}\le \frac{1}{c_1\sqrt{l}}$

成立的概率不低于 $1-{\text{e}}^{-c_{2}l}$ 。

类似地，有 ${\Vert {\Omega }_1^{\text{T}}\Vert }_2\le a_1\sqrt{n}$ 成立的概率不低于 $1-{\text{e}}^{-a_{2}n}$ ，则 ${\Vert L_y{\left({\Omega }_1^{\text{T}}{P}^{\text{T}}{L}_y\right)}^{†}{\Omega }_1^{\text{T}}\Vert }_2\le \frac{a_1\sqrt{n}}{c_1\sqrt{l}}$ 成立的概率不低于 $1-{\text{e}}^{-a_{2}n}-{\text{e}}^{-c_{2}l}$ 。接下来估计 ${\Vert \left(I-L_y{L}_y^{†}\right)PA\Vert }_F$ 的上界。

对算法2，考虑对PY进行QR分解，即 $PY=QR$ ，则相应的可以得到 $L_y{L}_y^{†}=Q{Q}^{\text{T}}$ ，此外将引理2中的 $\Omega$ 用算法2中的 ${\Omega }_1$ 替换，同时取特殊的p值0，则有以下结论成立：

${\Vert \left(I-L_y{L}_y^{†}\right)PA\Vert }_F\le \sqrt{\frac{r{\sigma }_1^2{\sigma }_{r+1}^2{\Vert {\tilde{\Omega }}_2\Vert }_2^2{\Vert {\tilde{\Omega }}_1^{†}\Vert }_2^2}{{\sigma }_{r+1}^2{\Vert {\tilde{\Omega }}_2\Vert }_2^2{\Vert {\tilde{\Omega }}_1^{†}\Vert }_2^2+{\sigma }_1^2}+{\displaystyle \underset{i=r+1}{\overset{n}{\sum }}{\sigma }_i^2}}$

综上所述，可以得到算法2的误差界有如下结论。

定理1 在算法2的假设条件下，Cholesky分解的随机算法误差界满足：

${\Vert PA{P}^{\text{T}}-L{L}^{\text{T}}\Vert }_F\le \left(1+\frac{a_1\sqrt{n}}{c_1\sqrt{l}}\right)\sqrt{\frac{r{\sigma }_1^2{\sigma }_{r+1}^2{\Vert {\hat{\Omega }}_2\Vert }_2^2{\Vert {\hat{\Omega }}_1^{†}\Vert }_2^2}{{\sigma }_{r+1}^2{\Vert {\hat{\Omega }}_2\Vert }_2^2{\Vert {\hat{\Omega }}_1^{†}\Vert }_2^2+{\sigma }_1^2}+{\displaystyle \underset{i=r+1}{\overset{n}{\sum }}{\sigma }_i^2}}$

成立的概率不低于 $1-{\text{e}}^{-a_{2}n}-{\text{e}}^{-c_{2}l}$ 。

4. 数值结果

4.1. 不同过采样参数选取对于算法的精度及运行时间的影响

取固定阶数为1000 × 1000的奇异值快速下降的数据矩阵A，对于不同的参数用两种随机算法做十次独立的实验，并记录误差和运行时间分别取平均值为 $e_{RCH}$ 和 $e_{SPRCH}$ ， $t_{RCH}$ 和 $t_{SPRCH}$ 。

从图1中可以看出两种算法的误差精度都很高。但随着p值增加，SPRCH的误差逐渐减小而RCH的误差逐渐增大。图2中可以发现SPRCH在时间成本上更有优势。需要指出的是，大规模数据计算中读取成本比算法运行成本高很多，新算法SPRCH只需要读取原始矩阵A一次，而RCH至少要读取两次，新算法总体成本比RCH算法成本低。

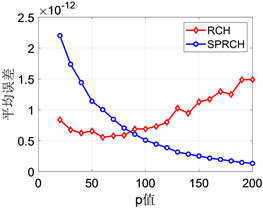
Figure 1. Error line chart for two algorithms for p from 20 to 200

图1. 参数p从20到200时两种不同算法的误差折线图

Figure 2. Line chart of running time for two algorithms for p from 20 to 200

图2. 参数p从20到200时两种不同算法的运行时间折线图

4.2. 不同规模矩阵对于算法的精度及运行时间的影响

根据上节选取合适的过采样参数，将这两种不同的算法和matlab中自带的Cholesky分解作比较，进行独立的十次实验，然后记录运行时间及误差分别取平均值为 $t_{CH}$ 、 $t_{RCH}$ 、 $t_{SPRCH}$ 和 $e_{CH}$ 、 $e_{RCH}$ 、 $e_{SPRCH}$ 。

Table 1. Comparison of three algorithms under different scale matrices

表1. 不同规模矩阵下三种算法的比较

从表1可以看出，随着矩阵规模不断增大，本文所提算法——Cholesky分解的单pass随机算法相对于传统的Cholesky分解以及主元随机Cholesky分解(RCH)算法在时间成本和误差上有着较大的优势。故新算法在应对大规模数据和流型数据矩阵的问题中有更好的应用前景。