材料弹性常数关系推导在材料力学教学中的应用研究

Research on the Application of Deriving the Relationship between Elastic Constants of Materials in the Teaching of Mechanics of Materials

摘要: 弹性模量、剪切模量和泊松比等弹性常数是材料力学和弹性力学中重要的知识点，也是后续力学课程学习的基础。各向同性线弹性材料只有两个独立的弹性常数，因此其弹性模量、剪切模量和泊松比之间具有直接关联关系。在力学基础教学中充分利用这一关系的不同推导方法，可将相关力学知识串联融合，加深学生的理解，同时也可拓展教师授课的深度和广度。鉴于此，本文分别梳理了在单向拉伸应力状态、纯剪切应力状态和一般应力状态下各向同性材料弹性常数之间关系的多种推导方法，并揭示了该关系式实质上是各向同性线弹性体弹性完全对称性的反映，以丰富教学素材，培养学生举一反三的创新实践能力。

Abstract: Elastic constants such as elastic modulus, shear modulus, and Poisson’s ratio are important knowledge points in the mechanics of materials and elasticity, and are also the foundation for subsequent mechanics courses. Isotropic linear elastic materials have only two independent elastic constants, so there is a relation between the elastic modulus, shear modulus, and Poisson’s ratio. By fully utilizing the different derivation methods of this relationship in basic mechanics teaching, relevant mechanical knowledge can be connected and integrated. This can deepen students’ understanding, and also expand the depth and breadth of teachers’ teaching. In view of this, this article summarizes various derivation methods for the relationship between the elastic constants of isotropic materials under different conditions such as uniaxial tensile stress state, pure shear stress state, and general stress state, and reveals that the relation between the elastic modulus, shear modulus, and Poisson’s ratio is essentially a reflection of the full symmetry of the isotropic linear elasticity, which can enrich teaching materials and cultivate students’ innovative practical ability.

1. 引言

弹性体的应力和应变之间通过弹性常数关联。常用的弹性常数有弹性模量E、剪切模量G和泊松比ν等，是材料力学和弹性力学等力学课程中的核心基本概念，对后续塑性力学、断裂力学、复合材料力学和机械设计等一系列力学及相关课程内容的理解也非常重要。各向同性线弹性材料只有两个独立的弹性常数，因此弹性模量、剪切模量和泊松比三者之间存在必然的联系，通常表示为：

$G=\frac{E}{2\left(1+\nu \right)}$ (1)

一些工科类的工程力学和弹性力学教程对这一关系不作推导，直接给出。面向力学专业的材料力学教材中，一般将这一关系的推导放在复杂应力章节介绍。尽管推导该关系式对力学初学者有一定难度，但可以加深其对应力、应变、弹性常数等概念的理解，也有利于提高其解决问题的综合能力，激发其探究意识和创新思维。因此，在材料力学教学中适时引入这一关系的推导，可提升课程内容的深度和广度，加强课程学习的挑战性和研究性。

鉴于此，本文系统梳理了多种推导弹性模量、剪切模量和泊松比之间关系的方法，由浅入深、从特殊到一般，并以推导过程为纽带，尽量将相关知识点融合串联起来，力图引导学生在推导过程中对所学知识举一反三、融会贯通。对应材料力学知识体系，文章分别在单向拉伸应力状态、纯剪切应该状态和一般应力状态进行弹性常数关系式的推导。第2节单向拉伸应力状态与第3节纯剪切应该状态下，都首先给出基于力平衡与几何关系分析的推导，便于初学者理解且物理意义清晰；后续的推导方法需要学习复杂应力状态、应变能密度和胡克定律。在第4节，在一般应力状态下推导出三个弹性常数关系式。

2. 在单向拉伸应力状态下推导

单向拉伸应力状态是学生最早接触也是最简单的应力状态。在此状态下推导弹性常数间的关系，可巩固学生对正应力和正应变、切应力和切应变、斜截面上的应力、泊松效应以及简单应力状态下的胡克定律等知识的理解。

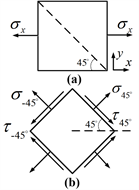
Figure 1. (a) Uniaxial tensile stress state; (b) 45˚ direction element

图1. (a) 单向拉伸应力状态；(b) 45˚方向微元体

取坐标系如图1(a)所示。单向拉伸应力状态下，微元体只有x (拉伸)方向存在正应力 ${\sigma }_x$ ，y方向正应力为零( ${\sigma }_y=0$ )，微元体上切应力为零( $\tau =0$ )。推导弹性常数的基本思路是利用45˚斜截面上(图1(b))的切应力( ${\tau }_{45°}$ )与单向拉伸正应力( ${\sigma }_x$ )关系(2)，以及45˚斜截面上切应变( ${\gamma }_{45°}$ )与单向拉伸正应变( ${\epsilon }_x$ )之间的关系(3)：

${\tau }_{45°}=\frac{{\sigma }_x}{2}$ (2)

${\gamma }_{45°}=\left(1+v\right){\epsilon }_x$ (3)

再将单向拉伸胡克定律 $\sigma =E\epsilon$ 、剪切胡克定律 $\tau =G\gamma$ 代入(2)与(3)，联立求得 $1/G=2\left(1+v\right)/E$ ，即三个弹性常数关系式(1)。

下文将给出关系式(2)、(3)的推导，其中2.1节和2.2节方法适合材料力学初学者，2.3和2.4节方法用到了复杂应力状态、应变能密度和广义胡克定律知识。

2.1. 分析法

首先用力平衡法推导45˚斜截面上的切应力与单向正应力之间的关系式(2)。取以x方向平面、y方向平面和45˚斜截面构成的三角形体元为研究对象(图1)，在45˚斜截面切向做力平衡分析，有 ${\tau }_{{45}^{\circ }}\sqrt{2}={\sigma }_x\sin 45˚$ ，简化即得到切应力与单向正应力关系(2)。

然后通过几何分析推导45˚斜截面上的切应变与单向正应变的关系(3) [1] 。如图2所示，假设边长为1的微元体在单向应力状态下，沿应力作用方向的单向正应变为 ${\epsilon }_x$ 。由于泊松效应，垂直于单向应力方向的正应变为 $-\nu {\epsilon }_x$ 。根据切应变定义(直角的变化量)，45˚斜截面上的切应变可由下式计算：

${\gamma }_{45°}/2=\pi /4-\arctan \frac{1-\nu {\epsilon }_x}{1+{\epsilon }_x}$ (4)

在小变形( ${\epsilon }_x$ << 1)情况下， $\frac{1-\nu {\epsilon }_x}{1+{\epsilon }_x}\approx \frac{\left(1-\nu {\epsilon }_x\right)\left(1-{\epsilon }_x\right)}{1-{\epsilon }_x^2}\approx \left(1-\nu {\epsilon }_x\right)\left(1-{\epsilon }_x\right)\approx 1-\left(1+\nu \right){\epsilon }_x$ ，因此 $\arctan \frac{1-\nu {\epsilon }_x}{1+{\epsilon }_x}\approx \frac{\pi }{4}-\frac{\left(1+\nu \right){\epsilon }_x}{2}$ 。代入(4)式，可得 ${\gamma }_{45°}=\left(1+\nu \right){\epsilon }_x$ ，即得到了切应变与单向正应变关系(3)。

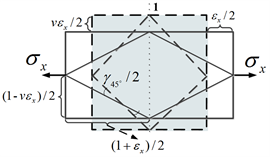
Figure 2. Deformation of element under the uniaxial tensile stress state

图2. 单向拉伸应力状态下的微元体变形

2.2. 公式法

根据材料力学知识 [2] [3] ，在单向拉伸应力状态下，方位角为α的斜截面上的切应力和切应变分别为：

${\tau }_{\alpha }=\frac{{\sigma }_x}{2}\sin 2\alpha$ (5)

${\gamma }_{\alpha }=\frac{{\epsilon }_x\text{-}{\epsilon }_y}{2}\sin 2\alpha$ (6)

直接可计算得到45˚斜截面上(图1(b)) ${\tau }_{45°}=\frac{{\sigma }_x}{2}$ ， ${\gamma }_{45°}=\left(1+v\right){\epsilon }_x$ ，即得到了切应力与单向正应力关系(2)和切应变与单向正应变关系(3)。

2.3. 应变能密度等效

单向拉伸应力状态下(图1(a))应变能密度可直接写为：

$u=\frac{1}{2}{\sigma }_x{\epsilon }_x=\frac{1}{2E}{\sigma }_x^2$ (7)

利用45˚方向微元体(图1(b))上的应力值 ${\sigma }_{{45}^{\circ }}={\sigma }_{-{45}^{\circ }}=\frac{{\sigma }_x}{2}$ ， ${\tau }_{45°}=\frac{{\sigma }_x}{2}$ 以及相应的应变值 ${\epsilon }_{{45}^{\circ }}={\epsilon }_{-{45}^{\circ }}=\frac{{\sigma }_x}{2E}\left(1-\nu \right)$ ， ${\gamma }_{{45}^{\circ }}=\frac{{\tau }_{{45}^{\circ }}}{G}=\frac{{\sigma }_x}{2G}$ ，可得：

$u=\frac{1}{2}{\sigma }_{{45}^{\circ }}{\epsilon }_{{45}^{\circ }}+\frac{1}{2}{\sigma }_{-{45}^{\circ }}{\epsilon }_{-{45}^{\circ }}+\frac{1}{2}{\tau }_{{45}^{\circ }}{\gamma }_{{45}^{\circ }}=\frac{{\sigma }_x^2}{4E}\left(1-\nu \right)+\frac{{\sigma }_x^2}{8G}$ (8)

由两种方式计算出的应变能密度相等，即 $\frac{1}{2E}{\sigma }_x^2=\frac{1}{4E}{\sigma }_x^2\left(1-v\right)+\frac{1}{8G}{\sigma }_x^2$ ，整理后可得到弹性模量、剪切模量和泊松比关系式(1)。

2.4. 广义胡克定律取单向拉伸应力状态

不少弹性力学教材在介绍广义胡克定律时，取单向拉伸应力状态代入广义胡克定律，并与简单拉伸实验结果对比，得到各向同性线弹性体弹性常数间的关系 [4] [5] [6] [7] 。为与弹性力学衔接，在此简单介绍这种处理方式。

将单向拉伸应力状态下的应力 ${\sigma }_x$ 、 ${\sigma }_y={\tau }_{xy}=0$ ，代入弹性力学中各向同性线弹性体广义胡克定律公式(见第3节)可得：

$\{\begin{array}{l}{\epsilon }_x=\frac{\lambda +\mu }{\mu \left(3\lambda +2\mu \right)}{\sigma }_x,{\epsilon }_y=\frac{-\lambda }{2\mu \left(3\lambda +2\mu \right)}{\sigma }_x\\ {\gamma }_{xy}=0\end{array}$ (9)

其中，λ和μ为拉梅系数，将在第3节作更多介绍。再根据单向拉伸实验结果，有：

$\{\begin{array}{l}{\epsilon }_x=\frac{1}{E}{\sigma }_x,{\epsilon }_y=-\frac{v}{E}{\sigma }_x\\ {\gamma }_{xy}=0\end{array}$ (10)

比较两式，并用工程参数表示拉梅系数为 $\lambda =\frac{Ev}{\left(1+v\right)\left(1-2v\right)}$ ， $\mu =\frac{E}{2\left(1+v\right)}$ ，另外拉梅系数μ就是剪切模量，即 $\mu =G$ 。这样就可以得到 $G=\frac{E}{2\left(1+v\right)}$ ，即得到弹性模量、剪切模量和泊松比关系式(1)。

3. 在纯剪切应力状态下推导

纯剪切状态(图3(a))是典型的简单平面应力状态，在此应力状态下推导弹性模量、剪切模量和泊松比之间的关系，简洁明了，易于理解。由材料力学定义，切应力为零的面为主平面，其上的正应力为主应力。图3(b)为纯剪切应力状态下的主应力微元体(微元体面上只有正应力没有切应力)。

Figure 3. Pure shear stress state

图3. 纯剪切应力状态

在纯剪切应力转态下证明弹性常数关系式(1)的基本思路是利用主应力( ${\sigma }_1$ , ${\sigma }_3$ )和切应力 $\tau$ 之间的关系(11)、主应变(ε₁或ε₃)和切应变γ之间的关系(12)，以及应力应变关系(广义胡克定律)来联立获得三个弹性常数之间的关系。根据材料力学知识(详见下文推导)，可知：

${\sigma }_1=\tau ,{\sigma }_3=-\tau$ (11)

${\epsilon }_1=\gamma /2$ (12)

同时，由广义胡克定律，有：

${\epsilon }_1=\frac{1}{E}\left({\sigma }_1-\nu {\sigma }_3\right),\gamma =\frac{\tau }{G}$ (13)

将式(11)、(13)，代入(12)，即可得到弹性常数相互关系(1)。

在复杂应力状态学习之前，学生尚未掌握广义胡克定律，因此需要利用叠加原理简单推导一下纯剪切状态下主应变和主应力之间的关系。根据简单拉伸状态下的胡克定律，由主应力 ${\sigma }_1$ 和 ${\sigma }_3$ 在第一主方向(±45˚斜截面法向)引起的正应变分别为：

${\epsilon }_{\pm 45˚}^{\left(1\right)}=\frac{{\sigma }_1}{E},{\epsilon }_{\pm 45˚}^{\left(3\right)}=-\nu \frac{{\sigma }_3}{E}$ (14)

基于线弹性小变形假设，由各应力引起的应变可进行叠加，于是有：

${\epsilon }_1={\epsilon }_{\pm 45°}^{}={\epsilon }_{\pm 45°}^{(1)}+{\epsilon }_{\pm 45°}^{(3)}=\frac{1}{E}\left({\sigma }_1-\nu {\sigma }_3\right)$ (15)

此即式(13)中的第一式。

下文将给出主应力和切应力关系(11)、主应变和切应变关系(12)的推导过程，学生掌握材料力学单向拉压和扭转章节知识后，就可以进行3.1节中的推导证明。3.2节的推导需要学生先学习复杂应力章节的相关公式。3.3和3.4是利用应变能密度和广义胡克定律进行证明。

3.1. 分析法

Figure 4. Deformation of element under the pure shear stress state

图4. 纯剪切应力状态下的微元变形

主平面(±45˚和±135˚斜截面)上的正应力(即主应力)可通过力平衡分析得到。如图3(c)所示，在45˚截面上由x和y方向的面力平衡，有 ${\sigma }_{1x}\sqrt{2}=\tau$ ， ${\sigma }_{1y}\sqrt{2}=\tau$ ，可得 ${\sigma }_{\text{1}}=\tau$ 。类似推导，可得 ${\sigma }_3=-\tau$ 。

这样就得到主应力和切应力关系式(11)。

主应变和切应变之间的关系(12)可通过对微元体的剪切变形作几何分析得到。如图4所示，设变形前微元的边长为1，切应变为γ，主应变为 ${\epsilon }_1=-{\epsilon }_3$ ，则有 $\frac{OD}{OC}=\tan \left(\frac{\pi }{4}-\frac{\gamma }{2}\right)=\frac{1/2+{\epsilon }_3/2}{1/2+{\epsilon }_1/2}=\frac{1-{\epsilon }_1}{1+{\epsilon }_1}$ ，在小变形(γ << 1)情况下 $tg\left(\frac{\pi }{4}-\frac{\gamma }{2}\right)=\frac{\tan \frac{\pi }{4}-\tan \frac{\gamma }{2}}{1+\tan \frac{\pi }{4}\tan \frac{\gamma }{2}}=\frac{1-\frac{\gamma }{2}}{1+\frac{\gamma }{2}}$ ，相互比较可得主应变与切应变关系 ${\epsilon }_1=\frac{\gamma }{2}$ ，此即主应变和切应变之间的关系(12)。

材料力学教程中基于几何分析获得主应变和切应变之间的关系式(12)的方法比较多，Timoshenko [8] 、Gere和Timoshenko [9] 认为，直接观测纯剪切应力状态下微元的变形即可得到关系式(12)，这需要一定的力学基础，材料力学初学者不一定好理解。Belyaev [3] 、Singh [10] 和同济大学的材料力学 [11] 采用做辅助线，Timoshenko和Goodier [12] 通过应用三角形正切公式，Gere和Goodno [13] 、文毅等 [14] 通过余弦公式，Philpot和Thomas [15] 通过应用正弦公式，分别对变形后的微元进行几何分析，得到主应变和切应变之间的关系式(12)，感兴趣的读者可以自行查阅资料。需要注意的是，这些几何分析中有些是基于简单剪切变形几何分析，这在小变形情况下是可以的。但在有限变形时，需要区分简单剪切与纯剪切，简单剪切会引起的Kelvin效应和Poynting效应 [16] [17] 。

3.2. 公式法

根据材料力学知识，纯剪切状态下，方位角为α的斜截面上的正应力和切应力分别表示为 [18] [19] [20] [21] ：

${\sigma }_{\alpha }=\tau \sin \left(2\alpha \right),{\tau }_{\alpha }=\tau \cos \left(2\alpha \right)$ (16)

显然，±45˚和±135˚斜截面上只有正应力没有切应力(图3(b))，因此是主平面，其上的正应力即为主应力，可求得为：

${\sigma }_1={\tau }_{\pm 45˚}=\tau ,{\sigma }_3={\tau }_{\pm 135˚}=-\tau$ (17)

即主应力和切应力之间的关系(2)。当然，上式也可直接应用材料力学中的主应力公式得到 [22] ，或者利用莫尔应力圆得到 [23] [24] 。

根据坐标变换下应变的变换公式，方位角为α的斜截面上的正应变和切应变分别表示为 [18] [19] [20] [21] ：

${\epsilon }_{\alpha }=\frac{\gamma }{2}\sin \left(2\alpha \right),{\gamma }_{\alpha }=\frac{\gamma }{2}\cos \left(2\alpha \right)$ (18)

因此，可得沿主平面(±45˚和±135˚斜截面)法向的正应变(即主应变)为：

${\epsilon }_1={\epsilon }_{\pm 45˚}=\gamma ,{\epsilon }_3={\epsilon }_{\pm 135˚}=-\frac{\gamma }{2}$ (19)

上式即给出了主应变和切应变之间的关系。应用材料力学中主应变的表达式 [22] ，或利用材料力学莫尔应变圆 [23] [24] 也可以得到主应变和切应变之间的关系式(12)。

3.3. 应变能密度等效分析

国内不少材料力学教材在介绍复杂应力状态下应变能密度时，通过对纯剪切应力状态下应变能密度分析来证明弹性常数相互关系式 [2] ，作为复杂应力状态下应变能密度应用的例子。为帮助学生更好地理解相关知识并把知识点相互联系，这里给出纯剪切应力状态下应变能密度等效的证明方式，并指出该推导方式与3.1和3.2节的分析是一致的。

纯剪切状态的应变能密度可用切应力和剪切模量表示 [2] 为：

$u=\frac{{\tau }^2}{2G}$ (20)

同时，也可通过主应力和弹性模量表示为：

$u=\frac{1}{2E}\left({\sigma }_1^2+{\sigma }_3^2-2\nu {\sigma }_1{\sigma }_3\right)=\frac{\left(1+\nu \right){\tau }^2}{E}$ (21)

两式比较，即推导得到弹性常数之间的关系式(1)。

换个角度看，将纯剪应力状态下微元体主应力的值代入到应变能密度公式：

$u=\frac{1}{2}\left({\sigma }_1{\epsilon }_1+{\sigma }_3{\epsilon }_3\right)$ (22)

再将主应力和切应力关系(11)代入(22)，可得到 $u=\tau {\epsilon }_1$ ，则直接有 $u=\tau {\epsilon }_1=\frac{1}{2}\tau \gamma$ ，化简后为 ${\epsilon }_1=\frac{1}{2}\gamma$ ，即主应变和切应变关系(12)。因此，应用应变能密度公式推导，实际也是把主应变和切应变关联起来，与3.1和3.2节的推导思路一致。

3.4. 广义胡克定律取纯剪切应力状态分析

取纯剪切应力状态下的主应力微元(图3(b))，将主应力 ${\sigma }_1=\tau ,{\sigma }_3=-\tau$ 代入弹性力学中各向同性线弹性体广义胡克定律公式(见第4节)有 ${\epsilon }_1=\frac{\tau }{2\mu }$ ， ${\epsilon }_2=-\frac{\tau }{2\mu }$ 。从主拉应力 ${\sigma }_1=\tau$ ，与主压应力 ${\sigma }_3=-\tau$ 线性叠加的效果，可得应变为 ${\epsilon }_1=\frac{\tau }{E}\left(1+v\right)$ ， ${\epsilon }_2=-\frac{\tau }{E}\left(1+v\right)$ 。相互比较，可得：

$\frac{\tau }{2\mu }=\frac{\tau }{E}\left(1+v\right)$ (23)

即有 $\mu =\frac{E}{2\left(1+v\right)}$ 。又 $\mu =G$ ，就可得 $G=\frac{E}{2\left(1+v\right)}$ ，即得到了弹性常数关系式(1)。

4. 在一般应力状态下推导

4.1. 对比弹性力学广义胡克定律与材料力学三向应力状态胡克定律分析

由弹性力学 [7] 知识可知，小变形情况下线弹性材料的应力应变关系满足 [4] [5] [6] [7] ：

${\sigma }_{ij}=E_{ijkl}{\epsilon }_{kl}$ (24)

其中， ${\sigma }_{ij}$ 为应力张量(表示法向为i的平面上沿j方向的应力分量，当i、j同向时为正应力分量简记为 ${\sigma }_i$ ，当i、j不同向时为切应力分量简记为 ${\tau }_{ij}={\tau }_{ji}$ )， $E_{ijkl}$ 为弹性张量(或刚度张量)， ${\epsilon }_{kl}$ 为应变张量(当i、j同向时为正应变分量简记为 ${\epsilon }_i$ ，当i、j不同向时为切应变分量简记为 ${\epsilon }_{ij}={\epsilon }_{ji}={\gamma }_{ij}/2$ )，重复下标遵守爱因斯坦求和约定。对完全各向异性材料，弹性张量含有21个独立分量。当材料为各向同性弹性体时，利用对称性可证明弹性张量只包含两个独立分量λ和μ (称为拉梅系数) [4] [5] [6] [7] 。此时，广义胡克定律表示为：

$\{\begin{array}{l}{\sigma }_x=2\mu {\epsilon }_x+\lambda \left({\epsilon }_x+{\epsilon }_y+{\epsilon }_z\right),{\tau }_{yz}=\mu {\gamma }_{yz}\\ {\sigma }_y=2\mu {\epsilon }_y+\lambda \left({\epsilon }_x+{\epsilon }_y+{\epsilon }_z\right),{\tau }_{zx}=\mu {\gamma }_{zx}\\ {\sigma }_z=2\mu {\epsilon }_z+\lambda \left({\epsilon }_x+{\epsilon }_y+{\epsilon }_z\right),{\tau }_{xy}=\mu {\gamma }_{xy}\end{array}$ (25)

材料力学中，直接从各向同性线弹性和小变形假设出发，利用叠加原理，得到三向应力状态下胡克定律：

$\{\begin{array}{l}{\sigma }_x=\frac{E}{1+v}\left[{\epsilon }_x+\frac{\nu }{1-2\nu }\left({\epsilon }_x+{\epsilon }_y+{\epsilon }_z\right)\right],{\tau }_{yz}=G{\gamma }_{yz}\\ {\sigma }_y=\frac{E}{1+v}\left[{\epsilon }_y+\frac{\nu }{1-2\nu }\left({\epsilon }_x+{\epsilon }_y+{\epsilon }_z\right)\right],{\tau }_{zx}=G{\gamma }_{zx}\\ {\sigma }_z=\frac{E}{1+v}\left[{\epsilon }_z+\frac{\nu }{1-2\nu }\left({\epsilon }_x+{\epsilon }_y+{\epsilon }_z\right)\right],{\tau }_{xy}=G{\gamma }_{xy}\end{array}$ (26)

两相比较 [25] ，马上可得：

$2\mu =\frac{E}{1+\nu },\lambda =\frac{E\nu }{\left(1+\nu \right)\left(1-2\nu \right)},\mu =G$ (27)

随即可得三个常用弹性常数之间的关系(1)。

4.2. 材料力学三向应力状态胡克定律完全弹性对称分析

材料力学中三向应力状态下胡克定律(26)是由线性叠加得到，不含对各向同性情况下弹性对称性的描述。假设将坐标系Oxyz绕Oz轴旋转任意的角度θ，得到新坐标系 $O{x}^{\prime }{y}^{\prime }{z}^{\prime }$ ，有 $x^{\prime }=x\cos \theta +y\sin \theta$ ， $y^{\prime }=-x\sin \theta +y\cos \theta$ ， $z^{\prime }=z$ 。利用坐标变换下应力与应变的变换公式，得到：

$\{\begin{array}{c}{{\tau }^{\prime }}_{xy}=\frac{1}{2}\left({\sigma }_y-{\sigma }_x\right)\sin 2\theta +{\tau }_{xy}\cos 2\theta \\ {{\gamma }^{\prime }}_{xy}=\left({\epsilon }_y-{\epsilon }_x\right)\sin 2\theta +{\gamma }_{xy}\cos 2\theta \end{array}$ (28)

由于各向同性线弹性体在任何方向都是弹性对称的，三向应力状态下胡克定律(26)在新坐标下依然成立，即有 ${{\tau }^{\prime }}_{xy}=G{{\gamma }^{\prime }}_{xy}$ 。将(28)代入其中，并取 $\theta ={45}^{\circ }$ 可得 ${\sigma }_y-{\sigma }_x=2G\left({\epsilon }_y-{\epsilon }_x\right)$ 。另外，由(26)直接有 ${\sigma }_y-{\sigma }_x=\frac{E}{1+v}\left({\epsilon }_y-{\epsilon }_x\right)$ 。相互比较即得到弹性常数关系式(1)。

可以看到，完整的各向同性线弹性体本构关系由使用两个拉梅系数的弹性力学广义胡克定律(25)描述。使用工程弹性常数的材料力学中胡克定律(26)式，需要加上弹性常数关系式(1)，才是完整的各向同性线弹性体本构关系。换句话说，弹性模量、剪切模量和泊松比之间的关系，本质上是各向同性线弹性体弹性对称性的必然要求。

5. 结语

本文对弹性模量、剪切模量和泊松比相互关系式的各种推导方法进行了全面梳理，有利于在教学中引导学生对该问题的拓展思考。其中，基于应力平衡和几何分析的方法，尤其适合力学初学者独立推导，可帮助其理解相关概念和方法的物理含义。基于应变能密度和广义胡克定律的方法，可开拓学生视野，启发其创新思维。教学过程中，对力学理论基础较薄弱的非力学专业学生，可用2.1和3.1节中特殊情况下的推导方法，培养学生解决问题的能力；对力学专业和力学基础较好的学生，可引导其探索复杂应力状态下的推导，将相关知识点融会贯通，强化研究性教学，提升课程的高阶性、创新性和挑战度。

推导过程中涉及的应力状态、应变状态、复杂应力、坐标变换等概念，有助于学生将材料力学与弹性力学相关知识点相互关联，加强其对力学基本概念的掌握。此外，本文各推导过程覆盖大部分材料力学知识，涉及不少弹性力学基本概念，可以用在机械、船舶和土木类等研究生弹塑性力学课程中，帮助学生补基础。我们的教学实践表明，在研究生弹塑性力学教学时引入本文作为教学内容，可以帮助学生巩固基础和建立知识结构，取得较好的教学效果。

基金项目

宁波大学教研项目一般项目(JYXMXZD2022115)；浙江省自然科学基金基金(LY20A020002)；浙江省“十四五”研究生教学改革项目(机械类研究生弹塑性力学教学改革)；国家自然科学基金(12132008)。

NOTES

^*通讯作者。