基于模糊PID的折叠机控制方法研究

Research on the Control Method of Folding Machine Based on Fuzzy PID

摘要: 针对家纺产品折叠机在高速状态下折叠精度不足的问题，提出一种基于模糊PID算法的家纺产品折叠变频控制方案。根据折叠机系统的预横折模块，通过对折叠工艺，机械结构等分析，构建了变频电机控制传递函数的数学模型，设计了模糊PID控制器，制定了模糊规则。基于MATLAB和Simulink模块仿真，通过对精度误差和误差变化率的在线修正，得出PID和模糊PID的仿真结果。对比分析表明：在阶跃信号作用下，模糊PID控制所需上升时间和调节时间比PID控制的时间分别减少了56.7%和59.6%；加入扰动信号作用后，模糊PID控制表现了良好的抗干扰能力，扰动撤除后仅用0.018 s便回归稳态，比PID控制响应时间提升了74%，PID控制回归稳态后有微量稳态误差，且模糊PID鲁棒性更好。实验结果表明：模糊PID的折叠精度提高了44.4%，可以完成高质量的折叠。

Abstract: A frequency conversion control scheme for home textile product folding based on a fuzzy PID algo-rithm is proposed to address the issue of insufficient folding accuracy of home textile product fold-ing machines at high speeds. Based on the pre-folding module of the folding machine system, a mathematical model for the transfer function of variable frequency motor control was constructed by analyzing the folding process, mechanical structure, etc. A fuzzy PID controller was designed and fuzzy rules were formulated. Based on MATLAB and Simulink module simulation, the simulation results of PID and fuzzy PID are obtained through online correction of accuracy error and error rate of change. Comparative analysis shows that under the action of step signals, the rise time and ad-justment time required by fuzzy PID control are reduced by 56.7% and 59.6%, respectively, com-pared to PID control; After adding disturbance signals, the fuzzy PID control showed good an-ti-interference ability. After the disturbance was removed, it only took 0.018 seconds to return to a steady state, which increased the response time by 74% compared to PID control. After PID control returned to a steady state, there was a slight steady-state error, and the fuzzy PID robustness was better. The experimental results show that the folding accuracy of fuzzy PID has been improved by 44.4%, and high-quality folding can be achieved.

1. 引言

国内现有的折叠机，折叠工艺相对简单，折叠效率较低，只能满足特定的折叠需求。在此基础上，开发了一种可以包含不同折叠工艺的、多工序并行的纺品折叠机。为提高折叠机的折叠精度和运行速度，对折叠机的折叠变频控制方法进行研究，来实现高速运行状态下，折叠出的纺品能否符合折叠要求，达到折叠良品率，便于纺品的后续包装。

近年来，科研人员对家纺产品折叠控制策略进行了一系列研究。徐学正 [1] 通过输送带传送毛巾，当传感器检测毛巾到位后进行折叠，对折叠精度有了一定的提高，由于是开环控制，并不能满足很好的折叠精度需求，且只能完成一种特定种类的折叠方式。周杰 [2] 将电机和皮带搭建了毛巾折叠输送带，用编码器形成闭环以解决传统折叠方式精度不高的问题，有一定参考价值，但在精度上仍有一定的误差。

相关研究者从精度控制算法着手，将模糊PID控制算法用于变频电机的精度控制，取得了不错的控制效果。赵秉鑫 [3] 利用模糊PID设计了升降机的联动机构，提升了系统的响应速度。董红平 [4] 设计了一种恒张力模糊PID的纱布折叠机，稳态误差小，张力实时性好，满足了纱布折叠的生产需求，但是不能满足大型纺品的折叠需求。

本文基于折叠机系统的精度控制要求，为解决折叠过程中，由于高速折叠带来的折叠精度不足，折叠质量达不到要求的问题，设计模糊PID控制系统，搭建折叠机控制系统模型，通过系统动态性能、抗干扰性能以及鲁棒性仿真测试，通过对折叠系统进行试验，对折叠精度进行测量和分析，验证了系统的有效性，达到提高折叠精度的目的。

2. 折叠机核心机构

折叠机采用了功能模块设计，整体拼装的方式。针对不同的家纺产品，根据折叠工艺，可以设计不同的折叠流程。

折叠机预横折模块

折叠机由预横折、横折、二次横折、纵折、二次纵折、堆垛、下衬板和控制柜组成，如图1(a)所示为折叠机总体结构。

折叠模块利用传送带控制纺品向前运动，在控制点位上通过控制不同的折叠单元，来使纺品折叠到位，其控制原理有一定的共性，故选用其中折叠精度要求较高的预横折模块进行控制分析。当折叠尺寸不同，折叠时进料状态的不同、气刀吹气干扰等情况下，折叠机构的控制精度决定了纺品折叠的质量。

预横折模块将纺品折叠两次，纺品从左侧传送带经过传感器进入左折叠单元，通过推杆和气刀，将纺品中间送入折叠机构，通过传送带的运行来折叠纺品，折叠后进入右侧折叠单元。右侧折叠单元通过推爪和气刀对纺品进行换向，使纺品向折叠平台上运动，到达设定折叠尺寸后，通过变频电机的反向运动，使平台上的纺品和传送带上的纺品有重叠部分，完成折叠。通过搭建控制系统模型，结合模糊PID算法，提高纺品的折叠尺寸精度。如图1(b)为预横折模块装置结构图。

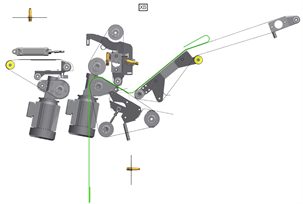
(a) 折叠机总体结构 (b)预横折模块装置结构

Figure 1. Overall structure diagram of folding machine and structure diagram of pre transverse folding module device

图1. 折叠机总体结构及预横折模块装置结构图

3. 预横折模块系统建模

3.1. 预横折模块右折叠单元模糊PID控制器

模糊PID算法是基于固定参数的传统PID算法 [5] ，将输入的误差和误差变化率精确量转换成为模糊化量，然后基于模糊逻辑关系及推理规则来模拟人的基于模糊概念的推理能力；再通过清晰化把模糊的控制量变换为实际用于控制的清晰量，通过知识库中的数据库和模糊控制规则库对PID参数进行整定，整定公式为：

$K_p=K_p+\Delta K_p$ (1)

$K_{\text{i}}=K_i+\Delta K_i$ (2)

$K_d=K_d+\Delta K_d$ (3)

式中 ${K^{\prime }}_P$ 、 ${K^{\prime }}_I$ 、 ${K^{\prime }}_D$ 分别为PID控制器中的整定参数初始值；ΔK_P、ΔK_I、ΔK_D分别为K_P、K_I、K_D的在线变化值。本文将模糊PID算法应用于纺品折叠控制系统中，选取了二输入三输出响应的模糊PID控制系统，预横折模块右折叠单元模糊PID变频控制系统框图如图2所示。

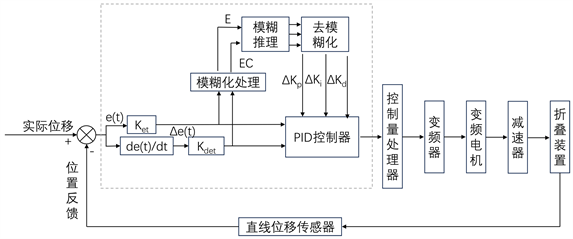
Figure 2. Block diagram of fuzzy PID variable frequency control system

图2. 模糊PID变频控制系统框图

根据折叠机构精度控制要求和实验可得，定义输入变量et( )、Det( )语言变量为E与EC，选取E与EC的基本论域分别为[−6, 6]和[−2, 2]，输入语言变量E和EC的论域均为[−6, 6]；定义ΔK_P、ΔK_I、ΔK_D对应输出语言变量为K_P、K_I、K_D，基本论域分别为[−30, 30]、[−20, 20]和[−0.2, 0.2]，输出语言变量K_P、K_I、K_D论域均为[−1, 1]。由上述变量论域可得输入变量e(t)和De(t)的量化因子为：K_et = 6/6=1，K_det = 6/2 = 3；输出变量ΔK_P、ΔK_I、ΔK_D的比例因子分别为：K₁ = 30/1 = 30，K₂ = 20/1 = 20，K₃ = 0.2/1 = 0.2。将输入与输出变量的论域均划分为7个模糊子集{NB (负大)、NM (负中)、NS (负小)、ZE (零)、PS (正小)、PM (正中)、PB (正大)}，输入参数的隶属函数要求在误差较小时具有高分辨率，从而拥有形状较尖的隶属函数；在误差较大时需要低分辨率模糊集，以稳定控制性能 [6] 。根据上述条件选用三角形和高斯相结合的隶属函数曲线作为控制器输入与输出变量的隶属函数，建立模糊论域与模糊语言变量等级之间的关系 [7] 。如图3和图4为对应的隶属度函数图。

Figure 3. E、EC membership functions

图3. E、EC隶属度函数

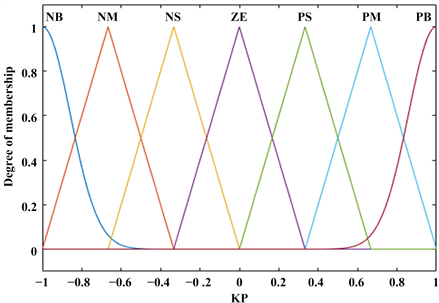
Figure 4. K_P、K_I、K_D membership functions

图4. K_P、K_I、K_D隶属度函数

依据K_P、K_I、K_D三个参数变化时对控制系统产生的不同影响，结合折叠控制经验，制定出以下三条调整规则 [8] ：

① 当位置误差│E│数值偏大时，为确保系统有较好的快速跟踪性能，增大K_P的数值加快系统响应速度，尽快消除偏差，减小K_D的数值来减小超调；同时减小K_I的数值，调小积分作用防止超范围控制。

② 当位置误差│E│和误差变化率│EC│数值为中等大小时，K_P的数值应减小，使系统有较小的超调量，而K_I和K_D的数值要适中，保证取值对系统的有较为合适的响应速度。其中K_D的取值对系统响应的影响较大。

③ 当位置误差│E│数值偏小时，K_P和K_I的数值都要增大，以确保系统有较好的稳态性能；当误差变化率│EC│偏小时，为避免系统在设定值附近有振荡，增强系统的抗干扰能力，当│EC│较小时，K_D的数值应增大；当│EC│较大时，K_D的数值应减小。

以上述制定的规则为基准，采用“IF A and B THEN C and D and E”多重多维条件语句的形式，得到关于参数K_P、K_I和K_D的模糊控制规则表，如表1所示。

Table 1. Fuzzy control rule table for parameters KP, KI, and KD

表1. 参数K_P、K_I和K_D的模糊控制规则表

3.2. 预横折模块右折叠单元传递函数

预横折模块右折叠单元控制系统是由主控模块、变频电机、变频器、减速器、传送带机构、直线编码器等组成的闭环控制系统，总传递函数表示为：

$G(S)=\frac{G_P\left(s\right)G_V\left(s\right)G_M\left(s\right)G_R\left(s\right)G_T\left(s\right)}{1+G_P\left(s\right)G_V\left(s\right)G_M\left(s\right)G_R\left(s\right)G_T\left(s\right)G_E\left(s\right)}$ (4)

G_P(s)、G_V(s)、G_M(s)、G_R(s)、G_T(s)、G_E(s)表示主控模块、变频器、变频电机、减速器、传送带机构、以及直线编码器的传递函数。主控模块将给定纺品运动距离的脉冲值与直线编码器反馈的纺品实际位置脉冲值的差值转化为控制电机运动的实际脉冲数，其传递函数可以当作比例环节，表示为： $G_P\left(s\right)=1/\left(100k{\theta }_1\right)$ ，将k以及q₁的值代入得其传递函数为： $G_P\left(s\right)=0.08$ 。

减速器可以近似为比例环节，可得其传递函数为： $G_R\left(s\right)=1/n_0$ ，代入减速比n₀的值可得： $G_R\left(s\right)=0.2$ 。

传送折叠装置将减速器减速后的齿轮带动皮带轮转动角位移转化为传送带带动纺品的直线位移，可以当作比例环节，比例值定义为k，则： $k=\left(\text{π}{d}_{0}i\right)/360$ ，代入d₀值得其传递函数为： $G_T\left(s\right)=k=4.707$ 。

直线编码器可以当作比例环节，其传递函数为： $G_E\left(s\right)=100$ 。

对于变频器的传递函数 [9] 设计，过推导可以得到其传递函数：

$G_V\left(s\right)=\frac{Y\left(s\right)}{U\left(s\right)}=\frac{K_1\left(1-{\text{e}}^{-\tau s}\right)}{s}$ (5)

可以把该系统近似为一个一阶的惯性环节，得到变频器的传递函数：

$G_V\left(s\right)=\frac{K_2}{T_{2}s+1}$ (6)

其中K₂为电压频率转换系数。变频器的电压范围为0~5 V，频率范围在0~50 Hz之间，因此其比例K₂ = 10 Hz/V。根据关系，设置加速时间为t为0.5，则T₂ = 0.6t。代入公式得到变频器的传递函数为：

$G_V\left(s\right)=\frac{10}{0.3s+1}$ (7)

系统采用DMA2-90L-8型三相异步变频电机，变频电机参数如表2所示。

Table 2. Variable frequency motor parameter table

表2. 变频电机参数表

忽略涡流损耗和磁滞效应等因素，根据电机运动方程简化其传递函数 [10] 为：

$G_M\left(s\right)=\frac{n\left(s\right)}{U\left(s\right)}=\frac{k_Q}{J_{Q}s+\frac{k_Q{U}_{N}p}{60f_N}}$ (8)

式中，P_N为电机的额定功率，U_N为电机的额定电压，J_Q为转动惯量。K_Q为变频的调速增益。p为电机的极对数。

代入表2变频电机参数到式，通过计算得到变频电机传递函数为：

$G_M\left(s\right)=\frac{1.75}{s+0.93}$ (9)

将G_P(s)、G_V(s)、G_M(s)、G_R(s)、G_T(s)、G_E(s)各环节传递函数代入式(4)中，得控制系统总传递函数为：

$G\left(s\right)=\frac{1.32}{0.3s^2+0.28s+132.73}$ (10)

基于MATLAB/Simulink仿真平台结合MATLAB/Fuzzylogic工具箱进行仿真设计，使用加权平均法去模糊化代入各环节传递函数 [11] ，搭建出右折叠单元控制系统仿真模型，如图5所示。

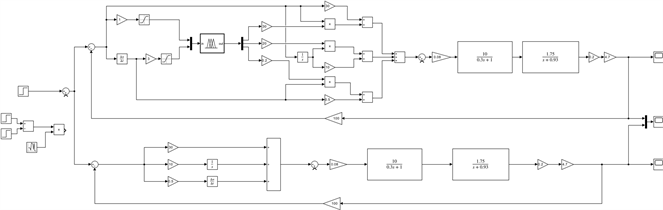
Figure 5. Simulation model of right folding unit control system

图5. 右折叠单元控制系统仿真模型

4. 模糊PID仿真及实验分析

4.1. 仿真分析

在t = 0 s时，输入一个单位阶跃信号，将求得的各环节传递函数写入Simulink仿真控制系统，根据经验试凑法 [12] 整定PID控制器参数。根据优化规则，经参数调试及响应曲线图效果分析，当K_P = 30、K_I = 10、K_D = 0.5时系统接近无超调量、响应速度快且调节时间短，控制效果最好，因此选取K_P = 30、K_I = 10、K_D = 0.5为整定好的初始值，仿真曲线如图6所示。

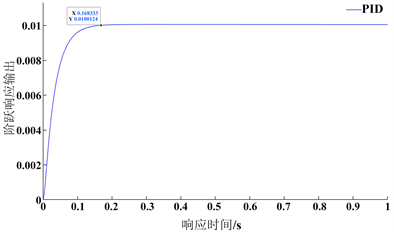
Figure 6. PID control simulation curve after parameter tuning

图6. 参数整定后 PID 控制仿真曲线

将整定的最优PID参数初始值K_P = 30、K_I = 10、K_D = 0.5分别输入到PID控制器和模糊PID控制器仿真平台中，在t = 0 s时输入单位阶跃信号，设1 s仿真时间，在理想测试环境下，模拟两种不同控制器系统的动态性能，得到仿真曲线和性能指标如图7所示。

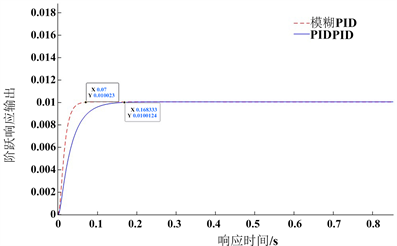
Figure 7. Dynamic performance test curve of PID control and fuzzy PID control

图7. PID 控制与模糊PID控制的动态性能测试曲线

由图7可知，PID控制系统与模糊PID控制系统的输出达到稳态值的90%，时间分别为0.0739 s与0.0320 s，两个系统分别在0.1683 s与0.0680 s输出达到稳态；对比PID控制，模糊PID控制所需的上升时间减少了56.7%，调节时间减少了59.6%，系统响应速度更快，上升时间和调节时间更短，动态性能和稳定性能更好，有利于折叠精度更高。

输入为阶跃信号时，得到的是理想环境下系统的动态性能，但纺品输送时有一定的干扰，如气刀的吹气次数，吹气间隔，吹气时间都会影响纺品的精度。为测试系统近似于实际工作时的控制效果和抗干扰能力，以单位阶跃信号作为输入，且PID参数初始值不变，仿真时间设为2 s，待系统跟踪阶跃信号达到稳定后，在t = 1 s加入方差为0.3、采样时间为0.01的正态分布随机扰动信号到控制系统中，作用时间设为0.3 s，得到系统抗干扰能力测试曲线如图8所示。测试结果表明，PID控制抗干扰能力较差，当受到扰动信号时，产生了较大振荡，超调量最大达到14%，且当扰动信号停止作用后，系统恢复稳态时间久，并伴有微量稳态误差；而模糊PID控制抗干扰能力较强，在扰动信号作用下影响较小，超调量最大达到5%，但是撤除扰动信号后仅用0.018 s就完全恢复稳态，相比PID控制响应时间提升了74%。模糊PID控制能减少外界因素带来的干扰，有更强的抗干扰能力，能够提升折叠质量。

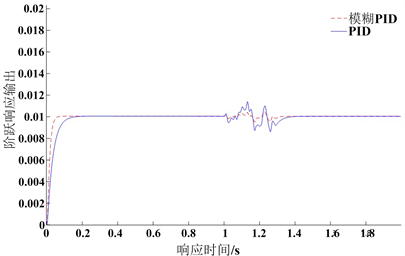
Figure 8. Test curve for anti-interference ability of PID and fuzzy PID control

图8. PID和模糊PID控制的抗干扰能力测试曲线

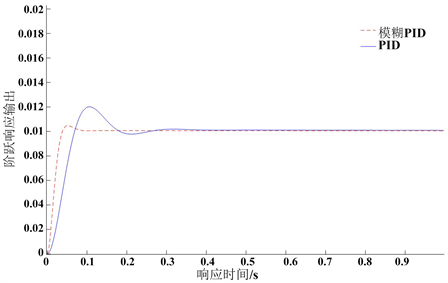
Figure 9. System response output curve with increasing moment of inertia

图9. 转动惯量增加时系统响应输出曲线

三相异步变频电机为折叠控制系统中主要的被控对象，系统实际工作时，由于减速器的作用和纺品进传送带的不同状态和类型，加上变频电机自身的非线性因素，会对其数学模型带来一定的变化。为进一步验证模糊PID控制策略的鲁棒性，在两控制器参数稳定不变的情况下，将变频电机传递函数的转动惯量的值增加20%，进行仿真测试。PID控制和模糊PID控制在转动惯量增加时的系统响应输出曲线和性能指标如图9所示。

在转动惯量增加20%的情况下，PID控制的超调量增加了20%，调节时间增加了38.4%；模糊PID控制的超调量增加了4%，调节时间增加了27.6%，变化率均小于PID控制。仿真测试表明了模糊PID控制鲁棒性更优越，能够适应高速度下的折叠。

4.2. 折叠实验分析

设定折叠尺寸在500 mm~1500 mm，间隔100 mm，做一次折叠实验，测量折叠精度，实验结果如表3所示。

Table 3. Variable frequency motor parameter table

表3. 折叠实验结果表

折叠结果表明普通PID控制的最大折叠误差为5.4 mm，模糊PID控制的最大折叠误差为3.0 mm，折叠精度提高了44.4%。模糊PID控制下的折叠尺寸误差均小于PID控制，故模糊PID控制下的折叠精度较高。

5. 结论

本文针对家纺产品折叠机的工作模式，进行折叠控制系统建模，通过PID控制和模糊PID控制算法对控制系统进行仿真分析和实验，得到如下主要结论：

① 基于折叠精度控制要求，设计了折叠机控制系统，并求解出系统传递函数，采用模糊PID算法来实现折叠精度控制，创建了折叠单元的数学模型，通过模糊推理方法在线整定PID参数，提高了系统的稳定性和抗干扰性。

② 通过MATLAB/Simulink仿真平台搭建步进定位控制系统仿真模型，以单位阶跃信号作为系统输入量，经调试确定PID参数初始值为K_P = 30、K_I = 10、K_D = 0.5。仿真结果表明，模糊PID控制所需上升时间和调节时间分别为0.0320 s与0.0680 s，PID控制所需上升时间和调节时间分别为0.0739 s和0.1683 s。加入扰动作用后，模糊PID控制恢复稳态仅需0.018 s，PID控制所需时间相对较长，且恢复稳态后有微量稳态误差。对比PID控制，模糊PID控制响应速度快、抗干扰能力和鲁棒性强，满足折叠装置的定位要求，为后续床单折叠和包装提供了基础。

③ 折叠实验结果表明：在设定尺寸为1500 mm时，普通PID最大误差为5.5 mm，模糊PID最大误差为3 mm，模糊PID算法的折叠精度相对于普通PID提高了44.4%。本文采用模糊PID控制算法来提高折叠机的折叠精度，为解决高速状态下折叠质量不高的问题提供了参考。

致谢

首先，感谢我的导师史伟民老师，在项目上和论文的选题、构思、定稿中悉心的指导。其次，感谢孙磊师兄和屠佳佳师兄，对我在项目上的帮助和在论文撰写期间提出的修改意见。同时，也感谢宏华数码股份有限公司在项目期间提供的帮助。我会继续努力，不断提高自己的学术水平。