基于数据幂变换的EEWMA高质量过程控制

EEWMA High-Quality Process Control Based on Data Power Transformation

摘要: 针对高质量过程的改进或恶化的监控问题，以服从指数分布的事件间隔时间(TBE)为监控指标，通过对TBE样本数据进行幂次为3.6的幂变换使其近似服从正态分布以改善分布的偏态性，在图统计量中同时考虑TBE的历史、当前以及最新变化信息以提高对TBE均值变化的敏感度，开发了基于数据幂变换的扩展指数加权移动平均控制图(PT-based EEWMA)，实现了对过程恶化、改进的监控。数值实验表明，相比于现有基于幂变换的EWMA、DEWMA控制图，PT-based EEWMA控制图在监测TBE均值偏移时，对不同方向、大小的偏移均表现出更好的ARL性能。更进一步，通过数值实验分析了真实分布为威布尔分布时，分布的形状、尺度参数的变化对指数分布下PT-based EEWMA控制图性能的影响。结果表明，该控制图对威布尔分布也具有一定的稳健性。

Abstract: Aiming at the problem of improvement or deterioration of high-quality processes, a power trans-formation-based extended exponentially weighted moving average control chart (PT-based EEWMA) is proposed, in which introducing the time between events (TBE) that follows an exponential dis-tribution as the monitoring indicator, transforming the TBE sample data with a power 3.6 to weak-en the skewness of its original distribution, and integrating the historical, current, and latest changes information of TBE in the control chart statistic to raise the sensitivity to shifts in the mean value of TBE, and at last the monitoring of process deterioration and improvement is achieved. Nu-merical experiments show that compared with the existing EWMA and DEWMA control charts, the proposed PT-based EEWMA control chart presents a better ARL performance for TBE mean shifts in different directions and sizes. Furthermore, the influence of the shape and scale parameters of the real distribution on the performance of PT-based EEWMA control chart under exponential distribu-tion is analyzed through numerical experiments. The results show that the control chart is also ro-bust to Weibull distribution.

1. 引言

随着科技的飞速发展，许多制造业、非制造业领域中的事件(如不合格品、缺陷)发生率低至百万分之一，这样被监测事件发生率极低的生产过程被称为高质量过程 [1] ，高质量过程中既定单位时间内事件的平均发生次数几乎为零，所以被观测事件的发生呈现低概率特性，这使得基于传统属性控制图(c控制图、p控制图、np控制图)存在高误报率、低检测效率等风险。幸运的是，事件的低发生概率恰恰对应大间隔时间，通过转换监测特征尺度，以两个相邻事件发生的间隔时间(Time Between Events, TBE)为质量特征，可以克服传统控制图缺陷，提高高质量过程监控性能 [2] 。另一方面，由于TBE的降低、增加分别意味着过程可能发生改进、恶化，而过程的恶化、改进与保证产品质量、改良生产设备等密切相关，所以及时监测过程的恶化、改进十分有必要。因此，开发基于TBE的双边控制图，以实现及时监测过程的改进、恶化情况 [3] 。

在事件发生率恒定的情况下，TBE可以用指数分布很好建模。而指数分布具有偏态性特点，这使得TBE不能直接应用基于正态分布传统控制图进行监测 [4] [5] 。Chan等 [6] [7] 先后提出了累积质量(Cumulative quantity control, CQC)控制图、累积概率控制(Cumulative probability control, CPC)图；C. W. Zhang等 [8] 发现这些基于传统概率极限的指数图存在平均运行长度(Average Run Length, ARL)偏差问题。Johnson [9] 指出若X服从尺度参数为的 $\theta$ 指数分布，则变换后的变量 $Y=X^{1/\alpha }$ 服从形状参数 $\alpha$ 和尺度参数 ${\theta }^{*}={\theta }^{1/\alpha }$ 的威布尔分布。Nelson、Liu [10] [11] 经分析发现幂次为3.6或2.5的变换，能够使得指数分布下的随机变量近似正态分布。2005年Montgomery [12] 解释了利用变量变换构建TBE控制图的思想并建议利用在小偏移监测方面表现良好的累计和(Cumulative sum, CUSUM)、指数加权移动平均(Exponentially weighted moving average, EWMA)控制图来进行监测。McCool等 [13] 证明了恰当的幂变换可以有效地提高EWMA控制图的性能。Santiago和Smith (2013) [14] 提出了添加运行规则后的休哈特控制图，进一步，为监测到小偏移，Aslam等 [15] 提出了变量变换下双边的双指数移动平均(double exponentially weighted moving average, DEWMA)控制图，发现其控制图的性能优于文献 [13] 。考虑到正态分布下DEWMA控制图比 EWMA控制图更灵敏的优点，Adeoti [5] 提出了基于变量变换的双边DEWMA控制图来监测遵循指数分布的质量特性，以改进文献 [15] 提出的EWMA控制图。

在高质量过程中，尽早发现过程恶化或过程的改进对减少生产过程中带来的损失或降低生产成本具有重要的意义。另一方面，考虑到高质量过程中突发事件可能引发灾难性损失，而这类事件会导致样本的最新差异信息陡变。Naveed (2018)等 [16] 提出的扩展指数加权移动平均(Extended Exponentially Weighted Moving Average, EEWMA)控制图，其是EWMA控制图的一种扩展形式，其利用了当前、过去的信息和当前的最新变化信息，实验证明，相对于EWMA控制图，EEWMA控制图对正态分布下的小偏移更具有灵敏性。

此外，注意到文献 [5] 、 [15] 分别利用概率的方法计算了所提控制图的ARL。Maragavio、Adams等 [17] [18] 指出，采用概率方法计算ARL不适用于CUSUM、EWMA等记忆型控制图。Haq等 [19] 指出，针对EWMA控制图以及其一些改进形式，在假设信号事件可以由一系列独立的伯努利随机变量表示下近似计算的ARL可能非常不准确，并认为需要使用马尔可夫链或计算机仿真模拟来重新评估。

综上，本文针对高质量过程中TBE的监控问题，结合EEWMA控制图的优点，并以指数分布下TBE作为过程质量的量化指标。通过幂次为3.6的幂变换，实现数据近似正态化，开发了指数分布下基于幂变换的EEWMA控制图，简称为PT-based EEWMA控制图。考虑到实际生产中事件发生率可能变化，因此分析了所提控制图在威布尔分布下的稳健性。同时，通过蒙特卡洛模拟重新评估了指数分布下基于3.6幂变换的EWMA和DEWMA控制图的ARL性能，并与变量变换后的PT-based EEWMA控制图进行比较。

2. 指数分布下基于数据幂变换的EEWMA控制图的设计

2.1. 现有正态分布下的双边EEWMA控制图

在本节我们简要介绍Naveed [16] 提出的正态分布下监控均值偏移的EEWMA控制图。假设随机样本 $X_t$ ， $t=1,2,\cdots$ 独立且服从正态分布，过程受控时均值、方差分别为 ${\mu }_0$ 、 ${\sigma }_0^2$ 。EEWMA控制图统计量定义为

$M_t={\lambda }_2\left(X_t-X_{t-1}\right)+\left({\lambda }_1-{\lambda }_2\right)X_t+\left[1-\left({\lambda }_1-{\lambda }_2\right)\right]M_{t-1}$ ， (1)

其中， ${\lambda }_1$ 和 ${\lambda }_2$ 为平滑系数， $\text{0}<{\lambda }_1\le 1$ ， $\text{0}\le {\lambda }_2<{\lambda }_1$ ，设 $M_0=X_0={\mu }_0$ ，“ $X_t-X_{t-1}$ ”表示当前最新的变化信息。整理(1)式可得

$M_t={\lambda }_1{X}_t-{\lambda }_2{X}_{t-1}+\left(1-{\lambda }_1+{\lambda }_2\right)M_{t-1}$ ， (2)

EEWMA控制图统计量的均值和方差分别为

$E\left(M_t\right)={\mu }_0$ ， (3)

$D\left(M_t\right)=\left[\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}\right]{\sigma }_0^2$ ， (4)

其中， ${\lambda }_3=1-{\lambda }_1+{\lambda }_2$ 。当 ${\lambda }_2=0$ 时，EEWMA控制图简化为具有时变控制限的EWMA控制图。EEWMA控制图的控制限表示为

$UCL={\mu }_0+k{\sigma }_0\sqrt{\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}}$ ， (5)

$LCL={\mu }_0-k{\sigma }_0\sqrt{\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}}$ ， (6)

k为控制系数，其值可通过指定的受控平均运行长度ARL₀确定。

2.2. 指数分布下基于幂变换的EEWMA控制图的设计

在高质量过程中，将事件间隔时间TBE记为随机变量X，则 $X~Exp\left(\theta \right)$ ，其概率密度函数为

$f\left(x\right)=\{\begin{array}{ll}\frac{1}{\theta }{\text{e}}^{-\frac{x}{\theta }}\hfill & x>0\hfill \\ 0\hfill & x\le 0\hfill \end{array}$ ， (7)

其中，尺度参数 $\theta >0$ ，X的期望 $E\left(X\right)$ 和方差 $V\left(X\right)$ 分别为 $\theta$ 和 ${\theta }^2$ 。设 $\theta =k{\theta }_0$ ， $k=1$ 表示过程处于受控状态， $k\ne 1$ 表示过程处于失控状态。 $X_t,t=1,2,3,\cdots$ 为X独立同分布的随机样本。

已知均值为 $\theta$ 的指数分布是尺度参数为 $\theta$ 、形状参数为1时的威布尔分布，即 $W\left(\theta ,1\right)$ 。并且经过幂变换 $Y=X^{1/\alpha }$ 后的变量Y仍服从威布尔分布，其形状参数和尺度参数分别为 $\alpha$ 和 ${\theta }^{*}={\theta }^{1/\alpha }$ ，根据文献 [10] ，经过 $\alpha =3.6$ 幂变换后的数据能够近似正态分布，因此，令

$Y=X^{1/3.6}$ ， (8)

其均值和方差分别为

$E\left(Y\right)={\theta }^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)$ ， (9)

$V\left(Y\right)={\left({\theta }^{1/3.6}\right)}^2\Gamma \left(1+\frac{2}{3.6}\right)-{\left[{\theta }^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)\right]}^2$ ， (10)

构建PT-based EEWMA控制图的统计量

$M_t={\lambda }_1{Y}_t-{\lambda }_2{Y}_{t-1}+\left(1-{\lambda }_1+{\lambda }_2\right)M_{t-1}$ (11)

$\text{0}<{\lambda }_1\le 1$ ， $\text{0}\le {\lambda }_2<{\lambda }_1$ ，令 $M_0=X_0={\theta }^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)$ 。PT-based EEWMA控制图统计量的均值和方差分别

$E\left(M_t\right)=E\left(Y_t\right)={\theta }^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)$ ， (12)

$\begin{array}{c}V\left(M_t\right)=\left[\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}\right]{\sigma }_Y^2\\ =\left[\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}\right]\left\{{\left({\theta }^{1/3.6}\right)}^2\Gamma \left(1+\frac{2}{3.6}\right)-{\left[{\theta }^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)\right]}^2\right\}\end{array}$ ， (13)

基于式(12)、(13)，构建在t点处的控制限

$UC{L}_t={\theta }^{1/3.6}\left\{\Gamma \left(1+\frac{1}{3.6}\right)+{\rho }_M\sqrt{\left[\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}\right]\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]}\right\}$

$LC{L}_t={\theta }^{1/3.6}\left\{\Gamma \left(1+\frac{1}{3.6}\right)-{\rho }_M\sqrt{\left[\left({\lambda }_1^2+{\lambda }_2^2\right)\frac{1-{\lambda }_3^{2t}}{1-{\lambda }_3^2}-2{\lambda }_1{\lambda }_2{\lambda }_3\frac{1-{\lambda }_3^{2t-2}}{1-{\lambda }_3^2}\right]\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]}\right\}$

其中， ${\rho }_M$ 表示控制图系数，当 $M_t>UC{L}_t$ 或 $M_t<LC{L}_t$ 时，控制图在t点发出失控信号。

3. 性能评价

通常利用平均运行长度(ARL)对控制图的性能进行评价，ARL是控制图从开始监测到失控信号发出的TBE平均观测样本数，ARL₀指过程实际处于受控状态时的平均运行长度，所以ARL₀越大越好，使得控制图具有尽可能小的误报率；而ARL₁是过程处于失控状态时的平均运行长度，我们希望其越小越好，以保证控制图尽早检测到过程的偏移。

Margavio [17] 证明了在假设运行长度RL服从参数为p的几何分布背景下，利用 $\text{ARL}=\frac{1}{p}$ 计算ARL的方法不适用于记忆性控制图，Abbasi [19] 、Haq [20] 等人也指出这种利用概率近似求EWMA及其一些改进形式的控制图的ARL方法存在问题。因此我们用蒙特卡洛模拟方法重新计算文献 [5] 、 [15] 所提控制图的ARL，并与新提出的控制图进行比较分析。

3.1. 现有控制图

本小节主要对文献 [5] 、 [15] 提出的指数分布下基于3.6幂变换的EWMA、DEWMA控制图进行简单介绍。

3.1.1. 现有基于幂变换的EWMA控制图

Alsam等人 [15] 首先对指数分布的数据进行幂次为3.6的幂变换，基于式(8)经变换得到的 $Y_t$ ，定义在t时间点的图统计量

$E_t=\lambda Y_t+\left(1-\lambda \right)E_{t-1}$ ， (14)

其中平滑系数 $\lambda \in \left(0,1\right]$ ，统计量的均值和方差分别为 ${\mu }_E={\theta }_0^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)$ ， ${\sigma }_E^2=\frac{\lambda {\theta }_0^{1/3.6}}{2-\lambda }\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]$ ，控制限为

$UCL={\mu }_E+{\rho }_E{\sigma }_E={\theta }^{1/3.6}\left\{\Gamma \left(1+\frac{1}{3.6}\right)+{\rho }_E\sqrt{\frac{\lambda }{2-\lambda }\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]}\right\}$ ， (15)

$LCL={\mu }_E-{\rho }_E{\sigma }_E={\theta }^{1/3.6}\left\{\Gamma \left(1+\frac{1}{3.6}\right)-{\rho }_E\sqrt{\frac{\lambda }{2-\lambda }\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]}\right\}$ ， (16)

其中， ${\rho }_E$ 为控制图系数，当 $E_t>UCL$ 或 $E_t<LCL$ 时，控制图发出失控信号。

3.1.2. 现有基于幂变换的DEWMA控制图

Adeoti等人 [5] 开发了对指数分布数据进行幂次为3.6的幂变换下的DEWMA控制图，基于式(8)经变换得到的 $Y_t$ ，图统计量定义为

$\begin{array}{l}{E}_t={\lambda }_1{Y}_t+\left(1-{\lambda }_1\right)Y_{t-1}\begin{array}{cc}& 0<{\lambda }_1\end{array}\le 1\\ D_t={\lambda }_2{E}_t+\left(1-{\lambda }_2\right)D_{t-1}\begin{array}{cc}& 0<{\lambda }_2\end{array}\le 1\end{array}$ ， (17)

文献 [5] 分别对 ${\lambda }_1={\lambda }_2$ 、 ${\lambda }_2\ne {\lambda }_2$ 下的控制图性能进行了比较分析，结果表明， ${\lambda }_1={\lambda }_2$ 时控制图具有更好的监测性能。因此本文关注 ${\lambda }_1={\lambda }_2$ 时控制图的性能，设 ${\lambda }_1={\lambda }_2=\lambda$ ，此时图统计量的均值和方差分别为：

${\mu }_D={\theta }_0^{1/3.6}\Gamma \left(1+\frac{1}{3.6}\right)$ ， ${\sigma }_D^2=\frac{\lambda \left(2-2\lambda +{\lambda }^2\right){\theta }_0^{1/3.6}}{2-\lambda }\left(\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right)$

控制限为：

$UCL={\theta }_0^{1/3.6}\left\{\Gamma \left(1+\frac{1}{3.6}\right)+{\rho }_D\sqrt{\frac{\lambda \left(2-2\lambda +{\lambda }^2\right)}{2-\lambda }\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]}\right\}$

$LCL={\theta }_0^{1/3.6}\left\{\Gamma \left(1+\frac{1}{3.6}\right)-{\rho }_D\sqrt{\frac{\lambda \left(2-2\lambda +{\lambda }^2\right)}{2-\lambda }\left[\Gamma \left(1+\frac{2}{3.6}\right)-{\Gamma }^2\left(1+\frac{1}{3.6}\right)\right]}\right\}$

其中， ${\rho }_D$ 为控制图系数，当 $D_t>UCL$ 或 $D_t<LCL$ 时，控制图发出失控信号。

3.2. 控制图的性能比较

本节以ARL作为衡量指标，利用Monte Carlo模拟10,000次，指定 ${\text{ARL}}_0=370$ ，选取PT-based EEWMA控制图中 ${\lambda }_{\text{1}}=0.05,0.1,0.3,0.5$ ，对应 ${\lambda }_2$ 在 $\left(0,{\lambda }_1\right)$ 的范围内取不同的值，以实现在不同平滑系数下对控制图监测性能的全面分析，表1~4分别展示了新提出的PT-based EEWMA控制图与文献 [5] 、 [15] 提出的指数分布下基于3.6幂变换的EWMA、DEWMA控制图在不同平滑系数和不同大小、方向偏移下的ARL₁值。

Table 1. When λ 1 = λ = 0.05 , the ARL of EEWMA, EWMA, and DEWMA control chart

表1. ${\lambda }_1=\lambda =0.05$ 时，数据幂变换下EEWMA、EWMA、DEWMA控制图的ARL值

Table 2. When λ 1 = λ = 0.1 , the ARL of EEWMA, EWMA, and DEWMA control chart

表2. ${\lambda }_1=\lambda =0.1$ 时，数据幂变换下EEWMA、EWMA、DEWMA控制图的ARL值

Table 3. When λ 1 = λ = 0.3 , the ARL of EEWMA, EWMA, and DEWMA control chart

表3. ${\lambda }_1=\lambda =0.3$ 时，数据幂变换下EEWMA、EWMA、DEWMA控制图的ARL值

Table 4. When λ 1 = λ = 0.5 , the ARL of EEWMA, EWMA, and DEWMA control chart

表4. ${\lambda }_1=\lambda =0.5$ 时，数据幂变换下EEWMA、EWMA、DEWMA控制图的ARL值

模拟结果显示(见表1~4)：

1) 对于较大尺度的上、下偏移， ${\lambda }_1$ 固定时， ${\lambda }_2$ 越小，PT-based EEWMA控制图的ARL₁越小。而对于较小尺度的上、下偏移，相对较大的 ${\lambda }_2$ 对应的控制图ARL₁较低。此外，当 ${\lambda }_2$ 固定时， ${\lambda }_1$ 越小，PT-based EEWMA控制图的ARL₁越小。例如在k = 0.5的偏移下， ${\lambda }_2$ 固定为0.03， ${\lambda }_1$ 取0.05、0.1、0.3、0.5对应的ARL₁值分别为：18.11、21.32、50.56、107.46。

2) 对比指数分布下基于幂变换的EWMA控制图，除了当 ${\lambda }_1=0.5,{\lambda }_2=0.25$ 对应的PT-based EEWMA控制图在个别较大偏移下(如k = 0.1、5、7)的ARL₁略高于该EWMA控制图以外，对于其他不同大小的上下偏移，不同的平滑系数下的PT-based EEWMA控制图ARL₁均低于该EWMA控制图。

3) 对比指数分布下基于幂变换的DEWMA控制图，当 ${\lambda }_1$ 取值较小时，PT-based EEWMA控制图在大部分偏移下的ARL₁值都低于该DEWMA控制图(如 ${\lambda }_1=0.05,0.1$ )，对于较大的 ${\lambda }_1$ 取值(如 ${\lambda }_1=0.3,0.5$ )，PT-based EEWMA控制图在TBE均值的下偏移监测方面不如该DEWMA控制图表现好，但在TBE均值发生上偏移时，PT-based EEWMA控制图的性能均优于该DEWMA控制图。总的来看，较小的 ${\lambda }_1$ 值对应的PT-based EEWMA控制图的性能优于指数分布下基于幂变换的DEWMA控制图，并且当 ${\lambda }_1$ 取值较大时，在监测下偏移方面，控制图也具有更好的监测性能。

总的来说，针对TBE均值不同大小、方向下的偏移，PT-based EEWMA控制图整体上表现更好，并且两个平滑系数的引入使得控制图能够更加灵活地用于对不同大小偏移的监测。

4. PT-based EEWMA控制图对威布尔分布的稳健性分析

上述内容是基于事件发生率不变，即事件间隔(TBE)服从指数分布的假设下进行的研究，鉴于实际高质量生产过程中，事件发生率可能随着时间发生变化，此时威布尔分布是拟合TBE更好的模型。Liu等 [11] 分析了当TBE真实分布为威布尔分布时，指数分布下基于幂变换的EWMA图的稳健性。在本节我们假设事件之间的时间服从指数分布，分析当真实分布为威布尔分布时，指数分布下PT-based EEWMA控制图的稳健性。

威布尔分布 $W\left(\theta ,\beta \right)$ 的密度函数如下所示：

$f\left(x\right)=\frac{\beta }{\theta }{\left(\frac{x}{\theta }\right)}^{\beta -1}{\text{e}}^{-{\left(x/\theta \right)}^{\beta }}$

其中， $x>0,\theta >0$ ， $\theta$ 是尺度参数， $\beta$ 为形状参数。当 $\beta =1$ 时，威布尔分布简化为指数分布。设 $X~W\left(\theta ,\beta \right)$ ，已知经过 $Y=X^{1/3.6}$ 变换后，Y仍服从威布尔分布，即 $W\left({\theta }^{1/3.6},3.6\beta \right)$ ，其均值和方差分别为：

$E\left(Y\right)={\theta }^{1/3.6}\Gamma \left(1+\frac{1}{3.6\beta }\right)$

$D\left(Y\right)={\theta }^{{\left(1/3.6\right)}^2}\left[\Gamma \left(1+\frac{2}{3.6\beta }\right)-{\Gamma }^2\left(1+\frac{1}{3.6\beta }\right)\right]$

文献 [11] 利用马尔可夫链方法分析了对指数分布数据进行双平方根变换后的EWMA控制图的ARL性能，发现其受控ARL仅与平滑系数、控制图系数有关，与尺度参数的大小无关，且此结论对真实分布为威布尔分布的情况也成立，即当形状参数固定不变时，尺度参数的变化不影响其受控ARL的值。

在本文我们利用蒙特卡洛方法验证了对指数分布TBE数据进行幂次为3.6的幂变换后的PT-based EEWMA控制图来说，上述性质同样成立。PT-based EEWMA控制图的受控ARL值仅与平滑系数 ${\lambda }_1$ 、 ${\lambda }_2$ 以及控制图系数的取值有关，不受指数分布下尺度参数变化的影响，且当真实分布为威布尔分布且形状参数不变时，控制图的受控ARL不受尺度参数变化的影响。然而在威布尔分布下，形状参数的变化会导致受控ARL发生变化。不失一般性，假设 ${\theta }_0=1$ ，展示当真实分布为威布尔分布时，不同的 ${\lambda }_1$ 和 ${\lambda }_2$ 平滑参数下形状参数 $\beta$ 变化对控制图的受控ARL性能的影响，详细见表5

从表5中可以发现， ${\lambda }_1$ 越小，控制图的稳健性越好。并且当 ${\lambda }_1$ 固定时， ${\lambda }_2$ 越小，控制图的稳健性越好，如 ${\lambda }_1=0.05,{\lambda }_2=0.01$ 时，对于(0.6, 4)范围内的 $\beta$ ，受控ARL始终在500的3%以内。

Table 5. When the real distribution is the Weibull distribution, the ARL0 of the EEWMA control chart based on the data power transformation

表5. 真实分布为威布尔分布时，数据幂变换下EEWMA控制图的ARL₀

表6、表7分析了在不同形状参数以及不同平滑系数选取下，面对不同大小、方向的偏移时控制图的性能。结果表明，形状参数 $\beta$ 的取值对失控情况下控制图的监测性能具有显著影响。对于不同大小的偏移， $\beta >1$ 时控制图对偏移的敏感度优于均比 $\beta <1$ ，此外， $\beta <1$ 时存在极大ARL₁值的现象，如 ${\lambda }_1=0.3$ ， ${\lambda }_2=0.03$ ， $\beta =0.7$ 时，ARL₁的值达到了1471.88。此外，随着形状参数的增大，控制图的监测性能越好。

Table 6. When the real distribution is the Weibull distribution, the ARL1 of the EEWMA control chart based on the data power transformation ( λ 1 = 0.1 )

表6. 真实分布为威布尔分布时，数据幂变换下EEWMA控制图的ARL₁ ( ${\lambda }_1=0.1$ )

Table 7. When the real distribution is the Weibull distribution, the ARL1 of the EEWMA control chart based on the data power transformation ( λ 1 = 0.3 )

表7. 真实分布为威布尔分布时，数据幂变换下EEWMA控制图的ARL₁ ( ${\lambda }_1=0.3$ )

5. 应用

在本节中，我们运用模拟数据集以及与尿路感染(UTI)相关的真实数据集来展示PT-based EEWMA控制图的实施过程，验证了PT-based EEWMA控制图相比于现有指数分布下基于幂次为3.6幂变换的EWMA控制图具有更好的监测性能。

5.1. 实例应用

利用构建的PT-based EEWMA控制图来实施对尿路感染(UTI)情况的监测，数据是来自文献 [14] 使用的来自大型医院系统的真实数据，此数据也先后被文献 [5] [15] 使用，该医院着重关注尿路感染的高发率，并通过监测在医院期间尿路感染患者的出院频率，以及时发现感染率是否有上升或下降的趋势。本节针对男性进行分析，数据见表8，已知男性UTI患者之间的平均时间为0.21天，我们可以假设受控状态的 ${\theta }_0=21$ 。不失一般性，指定 ${\text{ARL}}_0=370$ ，选取PT-based EEWMA控制图平滑系数 ${\lambda }_1=0.1$ ， ${\lambda }_2=0.05$ ，在选取指数分布下基于幂变换的EWMA控制图的平滑系数 $\lambda =0.1$ ，其控制图系数分别为2.688、2.687下，讨论我们的方法并与EWMA控制图进行比较分析，详细见图1。

Table 8. Urinary tract infection data

表8. 尿路感染(UTI)数据

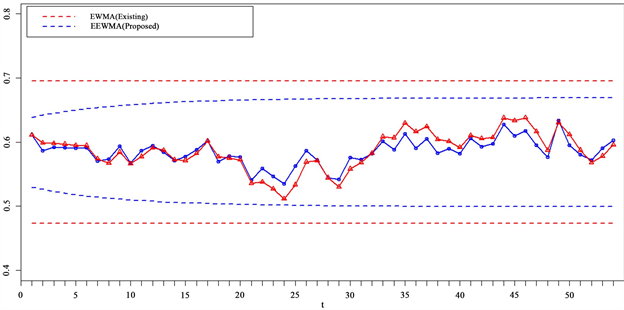
Figure 1. EWMA and EEWMA control charts based on the UTI data power transformation for monitoring data in Table 8

图1. 幂变换下用于监控表8中UTI数据的EWMA、EEWMA控制图

图1展示了利用PT-based EEWMA控制图、基于幂变换的EWMA控制图对UIT进行监测的实施过程，我们可以看到结果与原文献一致，即处于受控状态，可将PT-based EEWMA控制图用于对将来过程的监控。

5.2. 模拟应用

本节通过模拟数据来分析控制图的失控性能，假设两个连续事件之间的时间服从 ${\theta }_0=0.15$ 的指数分布，利用R软件生成54个来自 ${\theta }_1=0.15\times 1.7$ 指数分布下的模拟数据，将其视为来自失控过程的TBE观测值，即过程中发生了向上的偏移。实施基于幂次为3.6的幂变换下的EWMA、PT-based EEWMA方案，指定 ${\text{ARL}}_0=370$ ，选取PT-based EEWMA、EWMA控制图平滑系数分别为 ${\lambda }_1=0.1$ ， ${\lambda }_2=0.05$ ，详细的实施过程见图2

Figure 2. EWMA and EEWMA control charts based on the data power transformation for monitoring simulated data

图2. 幂变换下用于监控模拟数据的EWMA、EEWMA控制图

如图2所示，可以发现PT-based EEWMA控制图与幂变换下的EWMA控制图在监测性能方面存在差异，PT-based EEWMA控制图在第15个点处的值超出控制限，即发出失控信号，幂变换下的EWMA控制图在第21个点处发出失控信号，说明PT-based EEWMA控制图更早监测出偏移，即PT-based EEWMA控制图的监测性能优于幂变换下的EWMA控制图。

6. 结论

在高质量过程中，尽早发现过程的恶化或改进对减少生产过程中带来的损失或降低生产成本具有重要的意义。本文对服从指数分布的TBE进行幂次为3.6的幂变换使其近似服从正态分布，结合EEWMA控制图引入两个平滑系数、利用最新差异信息使控制图更加灵活且对中、小偏移更加敏感的优点提出了针对高质量过程监控的PT-based EEWMA控制图。数值实验验证了相比于EWMA，PT-based EEWMA控制图对各种尺度的均值偏移均具有较优的ARL性能。此外，在 ${\lambda }_1$ 值较小时，PT-based EEWMA控制图对上下偏移的敏感度优于相应的DEWMA控制图，并且当 ${\lambda }_1$ 取值较大时，PT-based EEWMA控制图在监测下偏移方面也表现出更好的监测性能。最后进一步研究了事件发生率随时间变化因而TBE服从威布尔分布的情形。数值实验表明，具有较小平滑系数的PT-based EEWMA控制图，对于服从威布尔分布的TBE数据亦具有相当的稳健性。

基金项目

长安大学中央高校基本科研业务费专项资金资助项目(310812163504)。

NOTES

^*通讯作者。