低速车辆在非结构化道路中的轨迹规划

Trajectory Planning of Low-Speed Vehicles on Unstructured Roads

摘要: 随着汽车保有量的不断增加，导致停车场数量逐渐减少。对于新手驾驶员而言，难以熟练地完成泊车活动。基于此现象，自动泊车技术得到了迅速发展。论文主要对自动泊车的轨迹规划算法进行了研究，通过联立最优控制问题中的车辆运动学约束、起始点约束、车辆速度及加速度约束以及代价函数，完成轨迹规划命题的建模。在命题求解时，选用全联立正交配置有限元法将其离散化为NLP问题，并对代价函数参数进行优化。通过Matlab和AMPL联合仿真求解得出符合约束条件的变量，并使得代价函数最小。实验结果表明，代价函数的优化方法使得车辆在泊车时具有更小的车辆运动前轮转角角速度变化，具备更优的行驶平顺性。

Abstract: With the increasing number of cars, the number of parking lots is gradually decreasing. It is difficult for novice drivers to skillfully complete parking activities. Based on this phenomenon, automatic parking technology has developed rapidly. This paper mainly studies the trajectory planning algorithm of automatic parking, and completes the modeling of trajectory planning proposition through simultaneous constraints of vehicle kinematics, starting point, vehicle speed and acceleration and cost function in the optimal control problem. When solving the proposition, the fully simultaneous orthogonal collocation finite element method is used to discretize it into NLP problem, and the parameters of the cost function are optimized. Through the joint simulation of Matlab and AMPL, the variables that meet the constraint conditions are obtained and the cost function is minimized. The experimental results show that the optimization method of cost function makes the vehicle have less angular velocity change of front wheel angle and better ride comfort when parking.

1. 引言

随着计算机科学技术、人工智能技术的不断发展，具有自主导航功能的移动机器人得到了广泛应用。轨迹规划是实现移动机器人自主导航的一项关键技术，其主要作用是基于车辆所处的环境，规划出一条满足机器人运动学约束的轨迹规划。

对于局部路径规划而言，文献 [1] 对全局路径进行分段，提取关键子节点，基于关键子节点通过DWA算法进行局部路径规划。文献 [2] 对DWA算法的评价函数进行了优化，提高了无人车的避障效率，提高了路径质量。文献 [3] 提出一种融合全局路径和局部路径的全局动态路径规划方法，提高了动态障碍物下较大较多环境下机器人的避障功能。对于采样的轨迹规划算法，Chu等人 [4] 提出一种在弗莱纳坐标系下基于全局参考路径进行横向采样的静态障碍物避障路径规划方法，通过对路径的横向偏移量进行等间距采样，并采用三次参数样条拟合生成候选避障路径。Werling等人 [5] 通过分别对横向轨迹的位移、速度、加速度和纵向轨迹的时间、速度、加速度进行多重采样和轨迹拟合，并通过将纵、横向最优轨迹依据时间进行合并，得到最终的最优局部轨迹。Lim等人 [6] 采用先采样再优化的分层轨迹规划方法，上层行为规划通过在搜索空间中进行采样确定换道、车道保持、绕障等行为，根据上层采样结果，下层轨迹规划采用数值优化方法生成最优轨迹。对于基于样条曲线的轨迹规划算法，Gonzalez等人 [7] 在局部规划中采用Beziers曲线规划转弯场景下的路径，此类曲线的优点是计算成本低，不足是生成的路径不经过中间路径点，不能保证碰撞安全。Ziegler [8] 等在2014年提出了基于BERTHA持续优化的轨迹规划方法，并构建了基于车辆运动学和动力学的约束条件，同时加入了自车运行的舒适条件，用凸多边形表示静动态障碍物，最后设计出新的权重函数，此种优化方法类似于Bemporad教授的凸近似原理。彭晓燕、谢浩等在2020年提出一种基于离散优化的局部路径规划算法，该算法通过权重函数加权得到局部最优路径 [9] 。人工势场法具有计算量小、反应速度快、生成路径平滑等优点，被广泛用于运动规划系统的移动机器人中 [10] 。对于复杂环境下的轨迹规划算法，李柏研究了复杂约束下自动驾驶车辆运动规划方法研究，提高了自动驾驶车辆在复杂场景中的应用 [11] 。

本文采用全联立正交配置有限元法求解轨迹规划命题，并对目标车辆进行了运动学建模分析。在此基础上，增加了起始点约束、车辆速度及加速度约束，并设计合理的代价函数，其优势主要体现在可以满足多个约束的前提下，规划出合理的轨迹。然后对代价函数参数进行优化，使得车辆在泊车时具有更小的车辆运动前轮转角角速度变化，从而使得车辆在行驶过程中具有更优的平顺性。

2. 轨迹规划命题的构建

2.1. 最优控制问题的确立

车辆的轨迹规划任务是指在车辆的起始时刻运动状态与终止时刻运动状态之间计算出符合约束条件的行驶轨迹，其中约束条件主要体现在车辆内在的运动能力限制。另一方面，满足上述约束条件的轨迹往往不止一条，应通过某一指标式筛选优质的轨迹作为最终结果。由于轨迹规划任务中存在硬性约束条件和用于寻优的指标式，因此适合通过建立最优控制表达式来进行轨迹规划。求解连续最优控制问题，即求取控制变量 $u\left(t\right)$ 并确定终止时刻 $t_f$ ，使得代价函数如下所示：

$J=\varphi \left(x\left(0\right),u\left(t_f\right),t_f\right)+{\displaystyle {\int }_0^{t_f}L\left(x\left(t\right),u\left(t\right),t\right)\text{d}t}$ (1)

沿着相应的状态变量所形成的集合 $x\left(t\right)$ 取得最小值。其中 $x\left(t\right)$ 产生制约的因素包括：

车辆运动学约束：

$\frac{\text{d}x\left(t\right)}{\text{d}t}=f\left(x\left(t\right),u\left(t\right),t\right),t\in \left[0,t_f\right]$ (2)

起始点约束：

$\phi \left(t_f,x\left(0\right),x\left(t_f\right),u\left(0\right),u\left(t_f\right)\right)=0$ (3)

车辆速度及加速度约束：

$g\left(x\left(t\right),u\left(t\right),t\right)\le 0,t\in \left[0,t_f\right]$ (4)

2.2. 车辆运动学约束

车辆在车速不高的工况下，应用车辆运动学模型已能够符合实际需求，将车辆的前后轮分别向车体纵轴方向合并为虚拟单轮，通过确定虚拟前轮的转动角速度以及虚拟后轮的线加速度变量，可以以间接确定车辆的前轮转角、行驶速度等，进而实现车辆运动。具体车辆运动学模型如图1所示：

Figure 1. Vehicle kinematics model

图1. 车辆运动学模型

将自动驾驶车辆称为车辆i。根据运动学模型，车辆i在惯性坐标系中的运动过程受到以下微分方程组的限制：

$\frac{\text{d}}{\text{d}t}\left[\begin{array}{c}{x}_i\left(t\right)\\ y_i\left(t\right)\\ {\theta }_i\left(t\right)\\ v_i\left(t\right)\\ {\varphi }_i\left(t\right)\end{array}\right]=\left[\begin{array}{c}{v}_i\left(t\right)\cos {\theta }_i\left(t\right)\\ v_i\left(t\right)\sin {\theta }_i\left(t\right)\\ v_i\left(t\right)\tan {\varphi }_i\left(t\right)/L_w\\ a_i\left(t\right)\\ {\omega }_i\left(t\right)\end{array}\right]$ (5)

式中， $t\in \left[0,t_f\right]$ ； $\left(x_i\left(t\right),y_i\left(t\right)\right)$ 代表车辆的后轮轴中点坐标； $v_i\left(t\right)$ 及 $a_i\left(t\right)$ 分别代表车体纵轴方向的速度及加速度，以使车辆前进的方向为正方向； ${\varphi }_i\left(t\right)$ 为车辆前轮偏转角； ${\omega }_i\left(t\right)$ 为前轮偏转角速度； ${\theta }_i\left(t\right)$ 代表车辆姿态角， $L_f$ 为车辆前悬距离， $L_r$ 为后悬距离， $L_w$ 为前后轮轴距， $L_b$ 为车宽。

2.3. 起始点约束

在车辆运动的起始时刻 $t=0$ ，指定车辆所处的运动状态。以车辆i为例，则有

$\left[v_i\left(0\right),{\varphi }_i\left(0\right),x_i\left(0\right),y_i\left(0\right),{\theta }_i\left(0\right)\right]=\left[v_{0i},p_{0i},x_{0i},y_{0i},{\theta }_{0i}\right]$ (6)

式中， $\left[v_{0i},p_{0i},x_{0i},y_{0i},{\theta }_{0i}\right]$ 对应着车辆的运动状态信息。

在车辆运动的终止时刻，对车辆运动状态进行限制，车辆 在终止时刻停止可描述为：

$v_i\left(t_f\right)=0$ (7)

$a_i\left(t_f\right)=0$ (8)

${\omega }_i\left(t_f\right)=0$ (9)

${\varphi }_i\left(t_f\right)=0$ (10)

2.4. 车辆速度及加速度约束

车辆在运动过程中，它们能够将状态、控制变量限制在一定区间内，一般包括：

$\left|\varphi \left(t\right)\right|\le {\Phi }_{\max }$ (11)

$\left|a_i\left(t\right)\right|\le a_{\max }$ (12)

$\left|v_i\left(t\right)\right|\le v_{\max }$ (13)

$\left|{\omega }_i\left(t\right)\right|\le {\Omega }_{\max }$ (14)

式中， ${\Phi }_{\max }$ 、 $a_{\max }$ 、 $v_{\max }$ 、 ${\Omega }_{\max }$ 分别为各状态、控制变量的最值。 ${\Phi }_{\max }$ 代表车辆前轮转角 ${\varphi }_i\left(t\right)$ 的偏转角度最值； $v_{\max }$ 是车辆在低速场景中的最大安全行驶速度； $a_{\max }$ 与 ${\Omega }_{\max }$ 分别为线加速度、前轮转角速度设置的最值。

2.5. 代价函数表达式

满足车辆轨迹规划任务约束条件的轨迹不止一条，因此还需要设计特定的代价函数求解出最优的轨迹，可通过代价函数来进行最优轨迹的选取。

$J=w_1{J}_1+w_2{J}_2$ (15)

式中 $w_1$ 、 $w_2$ 为各性能指标函数对应的权重函数，相对较大的权重表示在整个代价函数中该部分所占的比重更大。

3. 轨迹规划命题的数值求解

3.1. 最优控制问题简化

为解决最优控制问题式中的代价函数式包含不利于统一求解的积分项部分，引入新的状态变量将积分型性能指标统一转化为末值型性能指标，因此最优控制问题式则可进一步抽象为以下形式：

$\min J\left(x\left(t_f\right),u\left(t_f\right)\right)$ (16)

$\frac{\text{d}x}{\text{d}t}=F\left(x\left(t\right),u\left(t\right)\right)$ (17)

$G\left(x\left(t\right),u\left(t\right)\right)\le 0,t\in \left[0,t_f\right]$ (18)

式中， $x\left(t\right)$ 代表被微分的状态变量； $u\left(t\right)$ 代表控制变量；J为代价函数；F代表常微分方程组中的代数函数部分；G包含了车辆起始点约束及车辆速度及加速度约束； $t_f$ 代表动态过程的终止时刻。求解最优控制问题时，需在满足约束条件的控制变量 $u\left(t\right)$ 以及 $t_f$ 的前提下，使得设计的代价函数最小，从而实现最优命题的求解。

3.2. 离散化处理

实验采用直接法将最优控制命题中的连续变量全部离散化，将其转化为非线性规划问题，通过求解非线性规划问题的数值最优解可间接得到最优控制命题的最优解。

全联立正交配置有限元法是用配置点上的插值函数来逼近原问题，在配置点上无离散化误差拉格朗日插值函数用于数值逼近，由于高阶插值会导致龙格现象，因此分段低阶插值是常用方式，通过选择正交配置点可使拉格朗日插值提高求解精度。同时将最优控制命题中的状态变量以及控制变量进行离散化，将其全部视为决策变量来进行求解，具体方法如下。

将时域 $\left[0,t_f\right]$ 划分为 $N_{fe}$ 段时长相等的有限元 $\left[t_{i-1},t_i\right]$ ：

$t_i-t_{i-1}=\frac{t_f}{N_{fe}},i=1,\cdots ,N_{fe}$ (19)

在有限元 $\left[t_{i-1},t_i\right]$ 上，采用拉格朗日插值函数形式对各变量进行描述，其中K取3进行计算。

$x\left(t\right)=\underset{j=0}{\overset{K}{{\displaystyle \sum }}}{l}_{xj}\left(\tau \right)x_{i,j}$ (20)

$u\left(t\right)=\underset{j=1}{\overset{K}{{\displaystyle \sum }}}{l}_{uj}\left(\tau \right)u_{i,j}$ (21)

$t=t_{i-1}+\left(t_i-t_{i-1}\right)\tau ,\tau \in \left[0,1\right]$ (22)

式中， $l_{xj}\left(\tau \right)$ 为微分变量 $x\left(t\right)$ 的拉格朗日基函数； $x_{i,j}$ 为微分变量的离散配置点； $l_{uj}\left(\tau \right)$ 为非微分变量 $u\left(t\right)$ 对应的拉格朗日基函数； $u_{i,j}$ 为非微分变量 $u\left(t\right)$ 的离散配置点；其中拉格朗日基函数 $l_{xj}\left(\tau \right)$ 、 $l_{uj}\left(\tau \right)$ 应满足以下关系：

$l_{xj}\left(\tau \right)=\underset{k=0,k\ne j}{\overset{K}{{\displaystyle \prod }}}\frac{\tau -{\tau }_k}{{\tau }_j-{\tau }_k}$ (23)

$l_{xj}\left(\tau \right)=\{\begin{array}{l}1,k=j\\ 0,k\ne j\end{array}$ (24)

$l_{uj}\left(\tau \right)=\underset{k=1,k\ne j}{\overset{K}{{\displaystyle \prod }}}\frac{\tau -{\tau }_k}{{\tau }_j-{\tau }_k}$ (25)

$l_{uj}\left(\tau \right)=\{\begin{array}{l}1,k=j\\ 0,k\ne j\end{array}$ (26)

拉格朗日插值多项式的具有一定的优势，其优势在于变量在各个配置点上的值恰好与其系数相等，如下式所示：

$t_{i,j}=t_{i-1}+\left(t_i-t_{i-1}\right){\tau }_j$ (27)

$x\left(t_{i,j}\right)=x_{i,j}$ (28)

$u\left(t_{i,j}\right)=u_{i,j}$ (29)

由于状态变量可导，所以相邻有限元连接处的节点上状态变量值也应该连续，故有下面的连续性条件：

$x_{i+1,0}=x_{i,k}=\underset{j=0}{\overset{K}{{\displaystyle \sum }}}{l}_{xj}\left(1\right)x_{i,j},j=1,\cdots ,N_{fe}-1$ (30)

完整的非线性规划问题如下：

$\min J\left(t_f\right)$ (31)

$\underset{k=0}{\overset{K}{{\displaystyle \sum }}}\left({\frac{d\left({{\displaystyle \prod }}_{m=0,m\ne j}^K\frac{\tau -{\tau }_m}{{\tau }_j-{\tau }_m}\right)}{\text{d}\tau }|}_{\tau ={\tau }_j}{x}_{i,k}\right)=\left(t_i-t_{i-1}\right)F\left(x_{i,j},u_{i,j}\right)$ (32)

$G\left(x_{i,j},u_{i,j}\right)\le 0$ (33)

$t_i-t_{i-1}=\frac{t_f}{N_{fe}},t_0=0,t_{N_{fe}}=t_f$ (34)

$i=1,\cdots ,N_{fe};j=0,\cdots ,K$ (35)

求解各有限元配置点 $x_{i,j}$ 、 $u_{i,j}$ 、 $t_f$ ，使得代价函数取得极小值，即完成非线性规划问题的求解。

4. 仿真实验与分析

4.1. 参数优化前的仿真实验结果

为了验证算法的有效性，在Matlab平台下进行仿真实验。设计代价函数如下：

$J=10t_f+{\displaystyle {\int }_0^{t_f}{\omega }_i^2\left(t\right)\text{d}t}$ (36)

选择车辆运动前轮转角角速度作为控制变量的代表性变量，选择车辆运动速度作为状态变量的代表性变量。将上述轨迹规划命题在Matlab中进行输出，可得到车辆运动前轮转角角速度与运动时间曲线、车辆运动速度与运动时间曲线以及车辆行驶轨迹曲线。从车辆运动前轮转角角速度曲线当中可以看出，角速度变化率相对较大，车辆泊车活动过程中平顺性相对较差，仿真实验结果如图2所示。

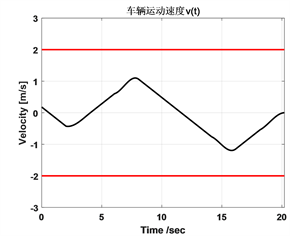
(a) (b)

Figure 2. Vehicle velocity curve before parameter optimization

图2. 参数优化前的车辆运动速度曲线

4.2. 参数优化后的仿真实验结果

上述实验中车辆运动前轮转角角速度变化较大，超出了边界值。对代价函数进行参数优化，调大车辆运动前轮转角角速度权重系数，如下所示。

$J=10t_f+10{\displaystyle {\int }_0^{t_f}{\omega }_i^2\left(t\right)\text{d}t}$ (37)

对代价函数参数进行优化后的车辆运动前轮转角角速度与运动时间曲线可以得出，车辆运动前轮转角角速度变化率相对较小，车辆运动平顺性相对较好，有利于增加驾驶员或乘客的舒适性，仿真实验结果如图3所示。

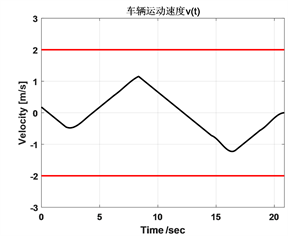
(a) (b)

Figure 3. Vehicle velocity curve after parameter optimization

图3. 参数优化后的车辆运动速度曲线

5. 结论

全联立正交配置有限元法可以在满足车辆运动学约束的基础之上，同时满足车辆起始点约束、车辆速度及加速度约束，并设计符合泊车条件的代价函数。提出了全联立正交配置有限元法代价函数的优化方法，通过对代价函数中的车辆运动前轮转角角速度参数进行调节，从而优化车辆运动轨迹。在上述设计下，车辆在泊车时具有更小的车辆运动前轮转角角速度变化，从而使得车辆在行驶过程中具有更优的平顺性，提高驾驶员以及乘客舒适性。