并联水库群调度规则提取的机理神经网络研究

Research on Mechanism Neural Network for Extracting Operation Rules of Parallel Reservoirs

摘要: 本文提出了基于理论指导的深度学习方法，提取并联供水水库联合调度规则，该方法以损失函数惩罚项的形式，将成员水库蓄水期弃水概率相等且供水期达到死库容状态概率相等、蓄水量边界约束和供水量边界约束加入到机器学习模型中。结果表明，在纯机器学习模型中耦合适当的调度机理知识可以提高其模拟水库调度规则的精度。在三种约束中，成员水库蓄水期弃水概率相等且供水期达到死库容状态概率相等对模拟结果的改善效果最佳。此外，同时耦合三种约束的场景模拟结果最优。

Abstract: In this paper, a theory-guided deep learning method is proposed for extracting the joint scheduling rules of parallel water supply reservoirs, which incorporates the equal probability of abandonment of the member reservoirs during the storage period, the equal probability of reaching the dead capacity state during the supply period, and the boundary constraints on the water supply into the machine learning model in the form of a penalty term of the loss function. The results show that coupling an appropriate amount of scheduling mechanism knowledge in the machine learning model can improve its accuracy in simulating reservoir scheduling rules. Among the three constraints coupled, equal probability of abandonment of member reservoirs during the impoundment period has the best improvement effect on the simulation results. In addition, the scenario that is coupled with the three constraints at the same time has the best simulation results.

1. 引言

水库群调度规则是指导水库群调度运行的重要工具，其基于当前时段的水库蓄水量、面临时段来水量等水文状况，对当前时段水库的出库流量、出力负荷等做出决策，进而达到提升水库的兴利效益。水库群调度规则提取的隐随机优化方法主要分为“模拟–优化”和“优化–拟合”两类。其中，“优化–拟合”方法是通过确定性优化模型，对具有长系列径流资料的水库进行优化调度，从而获得长系列最优调度决策过程。但是该优化方法主要用于确定水库群的最优调度决策过程，很难直接提取水库群的联合调度规则 [1] 。因此，需要利用回归分析、数据挖掘等方法，从长系列最优调度决策过程中提取出决策变量(如供水量、出库流量等)和运行要素(如水库当前时段蓄水量、用水户需水量、水库入库流量等)之间的函数关系(即调度规则)，进而对水库群进行优化调度。

基于“优化–拟合”方法提取水库调度规则的研究主要可以分为利用传统回归分析方法和神经网络等数据挖掘方法两类。Young [2] 首先提出通过最小二乘回归方法，确定调度策略和运行要素之间的函数关系，从而提取出水库调度规则。Karamouz等 [3] 应用线性回归方法，提取了水库蓄水量、入库流量和出库流量之间的函数关系。田峰巍等 [4] 提出了用于提取梯级水库群联合调度规则的多变量因子分析法和逐步回归分析法。然而传统方法在提取调度规则时往往存在选择基函数与求解系数的困难，难以准确提取复杂的非线性的调度规则。胡铁松等 [5] 首次提出使用BP神经网络方法提取水库群调度规则，为水库群调度函数的深入研究和实际应用开辟了一条全新且有效的途径。畅建霞等 [6] 基于改进的BP神经网络方法提取了西安市城市供水的三个水库的联合调度规则。吴佰杰等 [7] 运用改进的BP神经网络方法提取了六个水库组成的梯级水库群的调度规则。Zhang等 [8] 研究了ANN、SVM和LSTM模型三种人工智能模型的参数设置对模型在水库运行模拟中的性能的影响，并探讨了LSTM模型在水库运行模拟中的适用性。

然而，纯粹的机器学习模型只关注模型的输入项和输出项，计算过程缺乏水文见解，提取的调度规则可能违背客观规律或不符合调度原则 [9] 。Zheng等 [10] 将水库调度的水量平衡约束、单调性约束、出库流量边界约束整合到LSTM的损失函数惩罚项中，该模型的模拟结果更符合调度原理。据目前已有研究所知，Zheng等的工作是水库调度领域唯一使用理论指导的机器学习方法的研究。此外，现有的利用深度学习模型提取水库调度规则的研究多是针对单个水库或者将水库群系统等效为单库，对多水库系统调度规则提取的研究相对较少。然而现实中大多数库坝工程的建设运行多为并联或串联的形式，单库的研究成果在指导水库群联合调度的工程实践上存在局限性。因此，有必要提取多水库系统(尤其是并联水库系统)的运行规则，以克服单库调度规则难以指导多水库系统联合调度的不足。

针对上述问题和挑战，本文将机理知识纳入到深度学习模型中，提出了一种基于理论指导的LSTM模型，用于模拟和提取并联供水水库群的联合调度规则。

2. 理论指导的深度学习模型

2.1. 并联供水水库调度规则

仅有一个共同用水户的并联水库群系统，首先应确定共同用水户的总供水量，然后根据蓄水量空间分配规则进行供水任务的分配。本文采用的并联水库联合调度规则，组合使用供水与分配水规则进行联合调度。该规则基于两阶段调度模型，目标函数是使成员水库蓄水量尽量达到理想蓄水量，且供水总量尽量达到用水户的需水量。模型的约束条件包括水量平衡方程、成员水库蓄水量不超过水库最大库容且不低于死库容、供水量非负、总供水量不超过用水户的最大需水要求 [11] 。当所有成员水库都向用水户供水时，将水库群视为一个等效水库，以限制供水规则作为总供水量确定规则 [12] ，以参数式规则作为蓄水量分配规则组合构成并联水库联合调度规则 [13] 。优化得到的并联供水水库联合调度规则，可以使成员水库在蓄水期，同时发生弃水的概率相等，且在供水期，同时达到死库容状态的概率相等。

2.2. 理论指导的LSTM模型

传统的LSTM模型的损失函数仅考虑模拟值与真实值之间的误差，导致模拟出的水库供水量往往不具有物理一致性，不符合理论规则，提取出的调度规则也往往不够合理。因此，本文将水库调度的先验知识(Priori knowledge, PK)和边界约束(Boundary constraint, BC)转化为损失函数形式，并整合为LSTM模型损失函数的惩罚项，从而将先验知识和约束植入LSTM中得到一个改进的模型，用于提取水库调度规则。本文将该改进模型命名为理论指导的LSTM模型(Theory-guided LSTM, TG-LSTM)。

结合供水水库群联合调度的理论实际，本研究在深度学习模型中不仅使用了用于回归任务，计算预测值与真实值之间均方根误差的无机理约束损失函数，还集成了先验知识和边界约束两个部分。先验知识是指成员水库达到弃水状态的概率相等和达到死库容状态的概率相等，边界约束是指蓄水量边界约束和总供水量边界约束条件。建立的LSTM模型和TG-LSTM模型均为三层网络，包括一个输入层，一个隐藏层和一个输出层，所使用的无机理约束损失函数表示如下：

$Los{s}_{data}={\displaystyle \underset{i=1}{\overset{n}{\sum }}\sqrt{\frac{1}{n_t}{\left({\displaystyle \underset{t=1}{\overset{n_t}{\sum }}\left({\hat{R}}_{i,t}-R_{i,t}\right)}\right)}^2}}$ (1)

式中： $R_{i,t}$ 和 ${\hat{R}}_{i,t}$ 分别为t时段第i个成员水库供水量的实际值和模拟值； $n_t$ 为总时段数；n为并联水库系统中成员水库总数。

在并联水库调度中，为了使供水短缺最小化，需要各个成员水库的累计弃水量的期望值最低，即所有成员水库具有相同的弃水概率。如果每个成员水库都有相同的弃水概率，则意味着所有水库都在承担相同的弃水风险，从而确保不会存在某个水库频繁弃水而其他水库却蓄水过少的情况。通过均衡弃水概率，可以确保整个系统在满足用水需求的同时，最大程度地减少水资源的浪费 [14] 。而对于以供水为目标的并联水库系统，需要满足下式约束：

$P_i^{Max}\left(I_{i,t}>S_i^{Max}-S_{i,t}+E_{i,t}+R_{i,t}\right)={\lambda }^{Max},\forall i$ (2)

式中： $I_{i,t}$ 为第i个成员水库在第t时段的来水量， $S_i^{Max}$ 为第i个成员水库的总库容(最大蓄水量)， $S_{i,t}$ 为第i个成员水库在第t时段末的蓄水量， $P_i^{Max}$ 为第i个成员水库的弃水概率，各个成员水库的这一概率应相同，这样做的目的是防止某些水库比其他水库更频繁地面临蓄水量极端匮乏的情况，从而确保整个系统的稳定运行和供水安全 [14] 。同理，各个成员水库达到死库容状态的概率也应满足下式约束：

$P_i^{Min}\left(I_{i,t}<S_i^{Min}-S_{i,t}+E_{i,t}+R_{i,t}\right)={\lambda }^{Min},\forall i$ (3)

式中： $P_i^{Min}$ 为第i个成员水库达到死库容状态的概率，各个成员水库的这一概率应相同。将这两个先验知识约束整合到损失函数中可以写成 $Los{s}_{PK}$ ，如下式所示：

$Los{s}_{PK}=D\left({\hat{P}}_i^{Max}\right)+D\left({\hat{P}}_i^{Min}\right)$ (4)

式中： $D\left({\hat{P}}_i^{Max}\right)$ 和 $D\left({\hat{P}}_i^{Min}\right)$ 分别表示模拟结果所计算出的各个成员水库的弃水概率和死库容概率的方差。

各成员水库蓄水量边界约束，即各水库蓄水量应介于其死库容和最大库容之间。该约束可以表述为：

$S_i^{Min}\le {\hat{S}}_{i,t}\le S_i^{Max}$ (5)

将并联系统各成员水库的蓄水量约束整合到损失函数中，可以写为 $Los{s}_{BCS}$ ：

$g\left({\hat{S}}_{i,t}\right)=\{\begin{array}{l}{\hat{S}}_{i,t}-S_i^{Max},S_i^{Max}\le {\hat{S}}_{i,t}\\ 0,S_i^{Min}\le {\hat{S}}_{i,t}\le S_i^{Max}\\ S_i^{Min}-{\hat{S}}_{i,t},{\hat{S}}_{i,t}\le S_i^{Min}\end{array}$ (6)

$Los{s}_{BCS}=\sqrt{\frac{1}{n\times n_t}{\left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{t=1}{\overset{n_t}{\sum }}g\left({\hat{S}}_{i,t}\right)}}\right)}^2}$ (7)

并联水库系统总供水量边界约束条件，即各成员水库总供水量应不小于0且不大于共同用水户的需水量。该约束可以表述为：

$0\le R_t^{total}\le D_t$ (8)

式中： $R_t^{total}$ 为第t时段并联水库系统对共同用水户的总供水量，定义为成员水库供水量之和。 $D_t$ 为第t时段共同用水户的需水量。将并联系统总供水量约束整合到损失函数中，可以写为 $Los{s}_{BCR}$ ：

$h\left({\hat{R}}_t^{total}\right)=\{\begin{array}{l}{\hat{R}}_t^{total}-D_t,D_t\le {\hat{R}}_t^{total}\\ 0,D_t^{Min}\le {\hat{R}}_t^{total}\le D_t\\ -{\hat{R}}_t^{total},{\hat{R}}_t^{total}\le 0\end{array}$ (9)

$Los{s}_{BCR}=\sqrt{\frac{1}{n_t}{\left({\displaystyle \underset{t=1}{\overset{nt}{\sum }}h\left({\hat{R}}_t^{total}\right)}\right)}^2}$ (10)

因此，整合了先验知识和约束的TG-LSTM模型的损失函数可以写为：

$Loss={\lambda }_{data}Los{s}_{data}+{\lambda }_{PK}Los{s}_{PK}+{\lambda }_{BCS}Los{s}_{BCS}+{\lambda }_{BCR}Los{s}_{BCR}$ (11)

式中： ${\lambda }_{data}$ 、 ${\lambda }_{PK}$ 、 ${\lambda }_{BCS}$ 和 ${\lambda }_{BCR}$ 为超参数，控制损失函数中每一项的权重，并且可以在训练过程中进行调整。通常，最初可以对所有项使用相等的权重，并且可以基于损失函数值进行进一步的调整以实现更理想的性能。

TG-LSTM的训练方法与LSTM类似，都是通过使用优化算法最小化损失函数来进行训练。

3. 研究区域概况及模型参数设置

3.1. 研究区域概况

辽宁省大连市是我国东北地区重要的港口与贸易城市。在大连市的水资源管理中，碧流河水库和英那河水库构成的并联水库系统扮演着至关重要的角色，在城市的用水、灌溉、环境和工业供水等方面发挥着重要作用(如图1所示)。其中，碧流河水库控制流域面积2085 km²，水库正常库容为71,459万m³，死库容为7000万m³，英那河水库控制流域面积692 km²，水库正常库容为23,766万m³，死库容为2208万m³。大连市供水的设计保证率为90%。

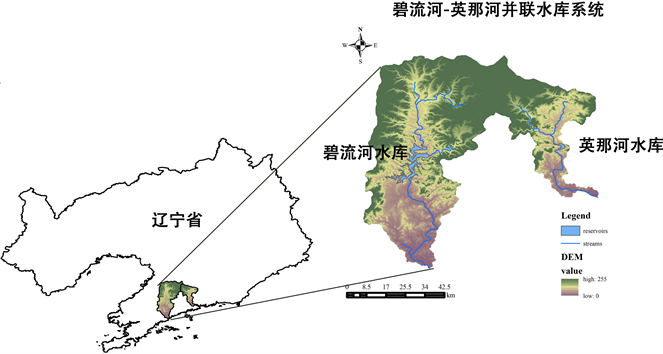
Figure 1. The location of the Biliu River-Yingna River parallel reservoir system

图1. 碧流河–英那河并联水库系统的地理位置

使用碧流河–英那河并联水库系统1951~2000年共50年的逐日实测来水量和需水量数据，计算出遵循该联合调度规则的逐日供水量，根据各成员水库的表面积计算得到各自的蒸发损失量。

3.2. 模型构建与输入

本研究采用了基于Python的TensorFlow框架来构建深度学习模型，用于提取水库调度规则。根据普遍接受的“6:2:2”分割规则 [15] ，将1951年至1980年共30年的逐日数据用作验证数据集，共10,958天；1981至1990年共10年的逐日数据作为验证数据集，共3652天；1991年至2000年共10年的逐旬数据作为测试数据集，共3653天。

水库运行数据作为输入(决策变量)和输出(目标变量)导入模型。具体而言，输入包括各成员水库第t时段的入库流量、各成员水库第t时段初的蓄水量、各成员水库第t时段的蒸发量、用水户对各成员水库的第t时段单独需水量(成员水库各自的库下工业需水量以及农业灌溉需水量等)以及t时段用水户对并联水库系统的需水量(直供工业需水量)。因此，模型中包括9个输入。模型输出是水库的第t时段供水量。

为了与模型的一致性相匹配，所有原始数据都在−1.0到1.0的范围内进行了标准化，然后在模拟后转换为原始值，标准化方程如下：

$X=\frac{X_{ori}-\bar{X}}{\sigma }$ (12)

式中：X是标准化值， $X_{ori}$ 是原始值， $\bar{X}$ 是原始数据的平均值， $\sigma$ 为原始数据的标准差。所有模型的输入结构都是标准化的，以确保各模型之间公正的比较。

为了评估不同的约束对TG-LSTM性能的影响，本研究定义了以下5个场景：

S0：TG-LSTM的训练没有任何约束，即传统的LSTM；

S1：TG-LSTM的训练只考虑成员水库弃水概率相等和达到死库容概率相等约束；

S2：TG-LSTM的训练只考虑成员水库蓄水量边界约束；

S3：TG-LSTM的训练只考虑水库群的总供水量边界约束；

S4：TG-LSTM的训练同时考虑上述三种约束。

3.3. 模型精度评估指标

本文使用纳什效率系数(Nash efficiency coefficient, NSE)、均方根误差(Root mean square error, RMSE)、平均绝对误差(Mean absolute error, MAE)评估了不同模型模拟的精度。

1) 纳什效率系数(NSE)：

$\text{NSE}=1-\frac{{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(R_{i,t}-{\hat{R}}_{i,t}\right)}^2}}{{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(R_{i,t}-{\bar{R}}_{i,t}\right)}^2}}$ (13)

2) 均方根误差(RMSE)：

$\text{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}{\left(R_{i,t}-{\hat{R}}_{i,t}\right)}^2}}$ (14)

3) 平均绝对误差(MAE)：

$\text{MAE}=\frac{1}{n}{\displaystyle \underset{t=1}{\overset{n}{\sum }}\left|R_{i,t}-{\hat{R}}_{i,t}\right|}$ (15)

4. 结果

4.1. 不同场景模拟精度对比

表1总结了在训练和测试阶段五种场景模拟结果的平均精度。五种场景下，两水库在训练期的模拟结果都略优于测试期的模拟结果，这表明各个场景的模型泛化能力均较好。

在模拟精度方面，无任何约束的传统LSTM模型的模拟结果并不一定比有约束的场景的模拟结果更差。在加入了单一约束的三种场景中，S1表现出最优的性能，对碧流河水库模拟结果的纳什效率系数为0.79，比S0，S2和S3模拟结果的纳什效率系数分别高出0.06，0.09和0.05；对英那河水库模拟结果的纳什效率系数为0.77，比S0，S2和S3模拟结果的纳什效率系数分别高出0.06，0.09和0.05，这表明在LSTM中分别加入合适的单一约束可以提高模拟精度。同时加入三种约束的S4场景，模拟精度优于只加入一种约束的场景，是所有五种场景中模拟精度最高的。

Table 1. Evaluation of the accuracy of simulation results for each scenario

表1. 各场景模拟结果精度评估

4.2. 不同模型提取的调度规则对比

4.2.1. 总供水量确定规则

由于用水户逐月需水量差距较大，本文采用总供水量与总需水量的比值即供水率来衡量总供水量。优化调度策略和5种场景提取的总供水量确定规则图如图2所示，从图中可知，在总可利用水量较小时，S2和S4提取的总供水量确定规则与优化调度策略较为接近，S1提取的规则偏差较大，但这三种场景的供水率都是随着总可利用水量的降低而降低；而S0和S3场景无法正确提取总供水量确定规则，即使面对总可利用水量很小的情况，这两种场景依然按照较高的供水率供水。在总可利用水量较大，足以满足用水户需水量时，S0、S1、S2均有明显的供水率大于1的时段出现，而S3和S4场景则没有出现这种异常的时段，这表明耦合了供水量边界约束的场景可以有效减少供水量大于用水户需水量的时段。耦合了合适的机理知识的场景提取的总供水量确定规则更加接近优化调度策略，而同时耦合三种机理的场景提取结果最接近。

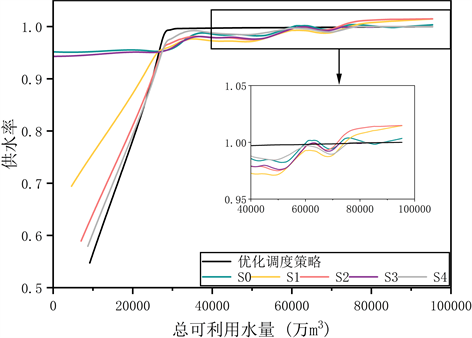
Figure 2. Rules of determining total water supply extracted by optimal operating strategy and each scenario

图2. 优化调度策略及各场景提取的总供水量确定规则

4.2.2. 蓄水量空间分配规则

图3给出了优化调度策略和五种场景提取得到的蓄水量空间分配规则。从图3可以看出，两座水库蓄水量均随着系统总蓄水量的增加而呈现出增加的趋势，并且在5种场景中，S1和S4的散点分布相对较集中，与优化调度策略更接近。S0、S1和S3的提取结果出现了成员蓄水量小于水库死库容甚至小于0的情况，这与实际的调度常识严重不符，这是因为在面对极端干旱情况时，耦合了蓄水量下限约束的场景(S2, S4)可以通过减少供水量来避免蓄水量低于死库容，而其他场景则不具有这种能力。

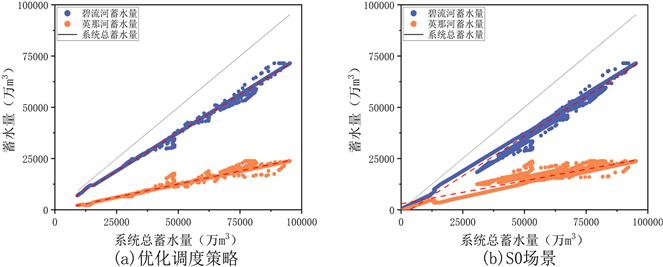
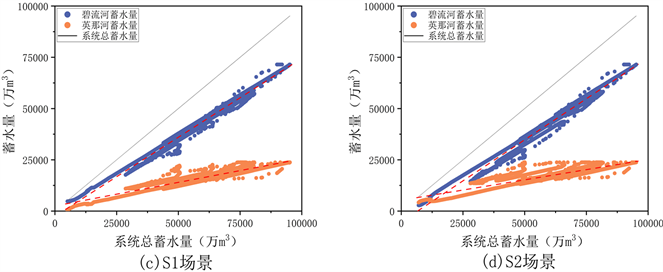
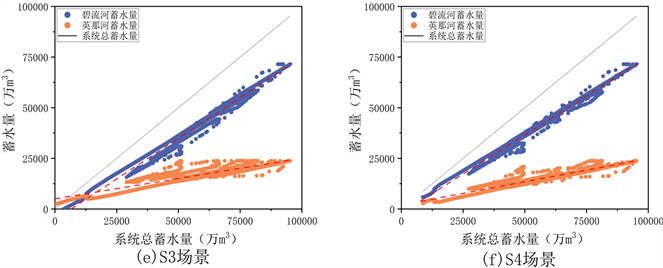
Figure 3. Long series water storage distribution state simulated by optimal operating strategy and each scenario

图3. 优化调度策略及各场景模拟的长系列蓄水分布状态

5. 结论与展望

本文开展了耦合机理的机器学习模型提取并联供水水库联合调度规则的研究，以损失函数惩罚项的形式考虑了并联供水水库系统成员水库弃水概率一致、死库容状态概率一致约束、蓄水量边界约束、供水量边界约束，构建了并联供水水库调度规则提取的耦合机理的深度学习模型。研究结果表明，在深度学习模型中耦合合适的机理知识，提取的调度规则更接近优化调度策略，可以获得比传统深度学习模型更高的精度。在设定的五种场景中，同时耦合了三种约束的场景总体上具有最好的提取性能，在模拟精度和提取的调度规则合理性方面均具有较好的结果。

耦合机理的机器学习方法可以被广泛应用于水资源调控系统的调度行为提取，为并联供水水库调度提供帮助，改变水库调度依赖人工经验的局面。未来的研究应集中于将并联水库系统、梯级水库系统以及混联水库系统的调度机理知识与机器学习模型耦合，用于水库调度规则的提取，并在水库调度实践中扩大耦合机理的数据驱动模型的使用。

基金项目

国家自然科学基金(52179022, 52209016)，以及水利部重大科技项目(SKS-2022119)资助。