基于灰色系统GM(1,1)模型的陕西省用水量预测分析

doi:10.12677/ORF.2024.141006

期刊菜单

基于灰色系统GM(1,1)模型的陕西省用水量预测分析
Predictive Analysis of Water Consumption in Shanxi Province Based on Grey System GM(1,1) Model

DOI: 10.12677/ORF.2024.141006, PDF, HTML, XML, 科研立项经费支持
作者: 付山贤：西安建筑科技大学管理学院，陕西西安
关键词: 灰色理论；GM(1；1)模型；用水量预测；残差修正；Grey Theory； GM(1；1) Model； Water Consumption Forecasting； Residual Correction

摘要: 为了解决地区间水资源分配不均和供需不平衡的问题，通过区域的用水量合理预测来优化水资源配置，对水资源的规划和管理具有十分重要的意义。文章使用传统灰色GM(1,1)模型和改进后的灰色GM(1,1)模型，从用水总量、生活用水量、生态用水量、农业用水量和工业用水量五个方面对陕西省用水量进行预测。结果表明：传统灰色GM(1,1)模型在用水总量、生活用水量、生态用水量方面精度更高，改进后的灰色GM(1,1)模型更适合在农业用水量和工业用水量方面的预测。文章使用精度最高的模型响应式对陕西省未来5年的用水量进行预测，对实际水资源调度决策具有参考价值。

Abstract: In order to solve the problems of uneven distribution of water resources and imbalance between supply and demand among regions, it is of great significance to optimize the allocation of water resources through reasonable forecasting of regional water consumption. This paper uses the traditional grey GM(1,1) model and the improved grey GM(1,1) model to predict the water consumption of Shaanxi Province from five aspects: total water consumption, domestic water consumption, ecological water consumption, agricultural water consumption and industrial water consumption. The results show that the traditional grey GM(1,1) model has higher accuracy in terms of total water consumption, domestic water consumption and ecological water consumption, and the improved grey GM(1,1) model is more suitable for forecasting agricultural water consumption and industrial water consumption. This paper uses the most accurate model to predict, which is of reactive use to predict water consumption in Shaanxi Province in the next five years, which has reference value for actual water resource scheduling decisions.

文章引用：付山贤. 基于灰色系统GM(1,1)模型的陕西省用水量预测分析[J]. 运筹与模糊学, 2024, 14(1): 61-72. https://doi.org/10.12677/ORF.2024.141006

1. 引言

水是生命之源，每个人时时刻刻都离不开水，城市区域的可持续发展也与水密不可分，随着社会经济的不断发展，用水量也在逐渐增长，为高效配置区域水资源，增强用水效率，防止因水资源供需不平衡影响社会经济以及生态环境的发展，对用水量进行合理预测是至关重要的。

目前对用水量进行预测常用的方法有用水定额法、时间序列法、BP神经网络法以及灰色系统理论等 [1] 。用水定额法中对用水定额的选取容易受不同时期社会经济发展的影响，时间序列法突出时间序列而不考虑外界因素影响，这两种方法预测偏差都较大；BP神经网络对模型收敛速度要求高且构建过程复杂。相比于这些方法，灰色系统理论具有时间序列短、统计数据少、信息不确定的系统建模分析特点，适合于对用水量进行预测。谢锦彪等 [2] 基于最小二乘法原理改进模型初始值参数；闫海霞等 [3] 利用飞蛾火焰算法建立MFO GM(1,1)优化模型；江艺羡等 [4] 利用黎曼积分，以不规则梯形面积取代传统梯形面积优化背景值。虽然众多学者均提出了改进模型，但未针对具体类型数据进行研究。

本文通过分析陕西省各部门用水量变化趋势，针对不同部门的具体数据提出相应改进措施，提高模型预测精度，具有良好的实践意义，可为相关单位优化分配水资源提供科学的数据参考资料，以保障城市的健康高质量发展。

2. 灰色系统原理

灰色系统理论由我国华中理工大学邓聚龙教授 [5] 于1982年提出，经历四十年的发展，已基本形成了一套完整的结构体系，包括以灰色代数系统、灰色方程、灰色矩阵等为基础的理论体系，以灰色序列生成为基础的方法体系，以灰色关联空间为依托的分析体系，以灰色模型(GM)为核心的模型体系，以系统分析、评估、建模、预测、决策、控制、优化为主体的技术体系，是进行建模、预测和评估的重要研究方法之一。灰色系统理论是一种用于解决信息不完备、结构体系不明确的系统的数学方法，通过对部分已知信息的生成、开发，提取有价值的信息，建立数学模型，进而实现预测未知信息的目的。其优良特性在于能够根据各因素之间的关联性和测度寻找隐藏于系统内部的变化规律，在建模过程中经过科学的处理方法，弱化原始数据的随机波动性，生成有规律的序列数据，构造相应的模型。

灰色预测是灰色系统理论的主要组成部分之一，相较于传统统计学预测而言，灰色预测能够充分挖掘少量数据中的内涵信息，以从较少的数据中得到较为合理的预测。其中最重要、使用最广泛的灰色预测模型是一阶微分GM(1,1)模型，其具有建模原理简单、可靠性和预测精度高等优点 [6] 。GM(1,1)模型将原始序列进行累加得到新的呈现一定规律的生成序列，随即建立灰色预测微分方程，用一阶线性微分方程的解对生成序列进行模拟，并对未来进行预测。目前，GM(1,1)模型在工业、农业、水利、经济、社会、科技、军事、医疗等多个领域的预测与评估方面都得到了广泛应用 [7] ，但是，这并不意味着GM(1,1)模型可以随意使用，其具有一定的适用范围。刘思峰等 [8] 应用模拟研究、实验分析等方法确定了GM(1,1)模型的有效区、使用区、不宜区和禁用区；徐宁等 [9] 提出背景值构造需同时满足的无偏性和最小误差性等条件；李峥 [10] 认为GM(1,1)的模型背景值序列存在取法固定、缺乏灵活性以及易受原始数据影响造成误差增大、结果失真等问题。

用水系统是多因素、多层次的复杂系统，其特点符合灰色系统理论的应用领域，又因GM(1,1)模型所需信息少、建模简单、易于检验，本文采用灰色GM(1,1)模型进行用水量预测是合适的。

3. 灰色预测模型的建立

3.1. 传统GM(1,1)灰色预测模型

构造灰色GM(1,1)模型具体步骤如下：

第1步：设GM(1,1)模型的非负原始数据序列为 $X^{(0)}$ ：

$X^{(0)} = (X^{(0)} (1), X^{(0)} (2), \dots, X^{(0)} (n))$ (1)

其中，n为观测数据个数；

为了弱化原始数据的随机性和波动性，增强数据的规律性，为灰色模型提供更加有效的信息，在建立灰色预测模型前，对原始数据做一次累加生成，即1-AGO (Accumulating Generation Operator)，记一次累加生成序列为 $X^{(1)}$ ：

$X^{(1)} = (x^{(1)} (1), x^{(1)} (2)), \dots, x^{(1)} (n)$ (2)

其中， $x^{(1)} (k) = \sum_{j = 1}^{k} x^{(0)} (j), k = 1, 2, \dots, n$ ；

第2步：准光滑检验：

$ρ_{k} = \frac{x^{(0)} (k)}{\sum_{i = 1}^{k - 1} x^{(0)} (i)}, k = 2, 3, \dots, n$ (3)

当 $\frac{ρ_{k + 1}}{ρ_{k}} < 1$ ； $ρ_{k} \in [0, q]$ ， $q < 0.5$ 时， $X^{(0)}$ 为准光滑序列；

第3步：准指数检验：

$σ (k) = \frac{x^{(1)} (k)}{x^{(1)} (k - 1)}, k = 2, 3, \dots, n$ , $σ (k) \in [a, b]$ (4)

令 $δ = b - a$ ，当 $δ < 0.5$ 时， $X^{(1)}$ 具有准指数规律；

第4步：由 $X^{(1)}$ 构造模型背景值序列 $Z^{(1)}$ ：

$Z^{(1)} = (z^{(1)} (1), z^{(1)} (2), \dots, z^{(1)} (n))$ (5)

其中， $z^{(1)} (k) = \frac{1}{2} (x^{(1)} (k - 1) + x^{(1)} (k)), k = 2, 3, \dots, n$ ；

第5步：建立GM(1,1)模型的灰微分方程为

$x^{(0)} (k) + a z^{(1)} (k) = b, k = 2, 3, \dots, n$ (6)

相应的白化方程为： $\frac{d x^{(1)} (t)}{d t} + a x^{(1)} (t) = b$ ；

其中，a为发展灰数，b为内生控制灰数；

第6步：采用最小二乘法确定参数：

${[a b]}^{T} = {(B^{T} B)}^{- 1} B^{T} Y$ (7)

其中 $B = [\begin{matrix} \begin{matrix} - z^{(1)} (2) & 1 \end{matrix} \\ \begin{matrix} \begin{matrix} - z^{(1)} (3) & 1 \end{matrix} \\ \begin{matrix} \begin{matrix} ⋮ & ⋮ \end{matrix} \\ \begin{matrix} - z^{(1)} (n) & 1 \end{matrix} \end{matrix} \end{matrix} \end{matrix}]$ ， $Y = [\begin{matrix} x^{(0)} (2) \\ \begin{matrix} x^{(0)} (3) \\ \begin{matrix} ⋮ \\ x^{(0)} (n) \end{matrix} \end{matrix} \end{matrix}]$ ；

第7步：确定GM(1,1)模型的时间响应序列：

${\hat{x}}^{(1)} (k + 1) = (x^{(0)} (1) - \frac{b}{a}) e^{- a k} + \frac{b}{a}, k = 1, 2, \dots, n$ (8)

第8步：对式(8)做一阶累减还原得 $X^{(0)}$ 的还原值为：

${\hat{x}}^{(0)} (k + 1) = (1 - e^{a}) (x^{(0)} (1) - \frac{b}{a}) e^{- a k}, k = 1, 2, \dots, n$ (9)

当 $k < n$ 时，所得数值为原始数据的拟合值；当 $k \geq n$ 时，所得数据为预测值。

3.2. 改进的GM(1,1)灰色预测模型

传统的GM(1,1)模型在建模时存在固有缺陷，有两处(参数、背景值)缺乏严格数学理论支撑，使模型不具备白指数率预测无偏性。为了弥补这些缺陷，求得最佳拟合函数，各领域学者进行不断探索，从不同角度改进模型，涌现出各种各样的改进算法。

大多学者针对参数或者背景值进行优化，考虑模型对高指数增长和低指数增长数据是否都适用，但对于用水量的趋势，一般都是平缓的增长，适用传统GM(1,1)模型。当精度不符合要求时，适用残差序列修正模型，先前的研究大多用于沉降量、灾害、故障率等的预测，很少将其用于需水量方面 [11] 。

设 $ε^{(0)} = (ε^{(0)} (1), ε^{(0)} (2), \dots, ε^{(0)} (n))$ ，其中， $ε^{(0)} (k) = ε^{(0)} (k) - {\hat{x}}^{(0)} (k)$ 。

对残差序列进行一次累加生成，建立微分方程，求出相应的残差修正时间响应式：

${\hat{x}}^{(0)} (k + 1) = (1 - e^{a}) (x^{(0)} (1) - \frac{b}{a}) e^{- a k} \pm (1 - e^{a_{ε}}) (ε^{(0)} (1) - \frac{b_{ε}}{a_{ε}}) e^{- a_{ε} k}$ 。

4. GM(1,1)模型的精度检验

为判断GM(1,1)灰色模型预测的准确性和可靠度，必须对模型的精度进行检验，当检验达到标准后，方可进行预测。本文采用残差检验和后验差检验来评价拟合预测效果。

4.1. 残差检验

残差序列 $e (k)$ 为：

$e (k) = x^{(0)} (k) - {\hat{x}}^{(0)} (k), k = 1, 2, \dots, n$ (10)

相对误差序列 $Δ$ ：

$Δ = (| \frac{e (1)}{x^{(0)} (1)} |, | \frac{e (2)}{x^{(0)} (2)} |, \dots, | \frac{e (n)}{x^{(0)} (n)} |)$ (11)

平均相对误差 $\bar{Δ}$ 为：

$\bar{Δ} = \frac{1}{n} \sum_{k = 1}^{n} Δ (k) = \frac{1}{n} \sum_{k = 1}^{n} \frac{| e (k) |}{x^{(0)} (k)}, k = 1, 2, \dots, n$ (12)

e表示预测值与真实值的接近程度，其值越小越好， $Δ$ 表示预测残差占原始数据的比例，其值越小越好。

4.2. 后验差检验

后验差检验时，GM(1,1)灰色模型的预测精度取决于均方差比值C和小误差概率p。均方差比值与小误差概率成反比关系，当均方差比值增大时，小误差概率将会降低，模型的预测精度也会较低。

4.2.1. 均方差比值

均方差比值C表示残差序列均方差与原始序列均方差之比，其值越小，误差越小，预测精度就越好，若 $C \geq 0.65$ 时，模型检验不合格。

原始序列均方差 $S_{1}$ 为：

$S_{1} = \sqrt{\sum_{k = 1}^{n} \frac{{[x^{(0)} (k) - {\bar{x}}^{(0)}]}^{2}}{n}}$ (13)

残差序列均方差 $S_{2}$ 为：

(14)

均方差比值C为：

$C = \frac{S_{2}}{S_{1}} = \sqrt{\frac{\sum_{k = 1}^{n} {[e (k) - \bar{e}]}^{2}}{\sum_{k = 1}^{n} {(x^{(0)} (k) - {\bar{x}}^{(0)})}^{2}}}$ (15)

式中， ${\bar{x}}^{(0)} = \frac{1}{n} \sum_{k = 1}^{n} x^{(0)} (k)$ ， $\bar{e} = \frac{1}{n} \sum_{k = 1}^{n} e (k)$ 。

4.2.2. 小误差概率

小误差概率p指残差与残差均值的差值的绝对值小于0.6745倍原始数据均方差的概率，其值越大，说明误差较小的概率越大，模型精度越高，若 $p \leq 0.70$ 时，模型检验不合格，精度不达标。

小误差概率p为：

$p = P {| e (k) - \bar{e (k)} | < 0.6745 S_{1}}$ (16)

式中， $\bar{e (k)}$ 为残差序列平均值。

4.3. 模型精度等级划分

GM(1,1)灰色预测模型精度检验等级划分标准见表1所示。

Table 1. Classification criteria for accuracy test of gray prediction models

表1. 灰色预测模型精度检验等级划分标准

5. 应用案例

陕西省位于我国西北地区，水资源相对比较匮乏，且分布不均，陕北、关中、陕南3个地区的水资源总量分别占全省水资源总量的9.8%、19.5%和70.7%，全省人均水资源占有量仅为1086 m³，约为全国平均水平的一半，是我国水资源最紧缺的省份之一 [12] 。水资源对于经济规模的增长至关重要，本文分析陕西省2010~2021年历年用水总量、农业用水量、工业用水量、生活用水量以及生态用水量数据，并对未来5年用水总量及各部门用水量进行预测。数据来源于陕西省水利局、《中国水资源公报》以及《陕西省统计年鉴》，见表2所示。

Table 2. Water consumption data of Shaanxi Province from 2010 to 2021

表2. 陕西省2010~2021年历年用水量数据

5.1. 灰色GM(1,1)预测模型的构建

(1) 建立原始数据序列并做一次累加生成

原始数据序列用水总量 $X_{0}^{(0)}$ ，农业用水量 $X_{1}^{(0)}$ ，工业用水量 $X_{2}^{(0)}$ ，生活用水量 $X_{3}^{(0)}$ ，生态用水量 $X_{4}^{(0)}$ ：

$X_{0}^{(0)} = [x_{0}^{(0)} (1), x_{0}^{(0)} (2), \dots, x_{0}^{(0)} (n)] = [83.4, 87.8, \dots, 91.8]$ ，

$X_{1}^{(0)} = [x_{1}^{(0)} (1), x_{1}^{(0)} (2), \dots, x_{1}^{(0)} (n)] = [57.4, 56.2, \dots, 54.6]$ ，

$X_{2}^{(0)} = [x_{2}^{(0)} (1), x_{2}^{(0)} (2), \dots, x_{2}^{(0)} (n)] = [11.8, 13.2, \dots, 10.9]$ ，

$X_{3}^{(0)} = [x_{3}^{(0)} (1), x_{3}^{(0)} (2), \dots, x_{3}^{(0)} (n)] = [13.2, 16.2, \dots, 20.3]$ ，

$X_{4}^{(0)} = [x_{4}^{(0)} (1), x_{4}^{(0)} (2), \dots, x_{4}^{(0)} (n)] = [1.0, 2.1, \dots, 5.9]$ ，

一次累加生成序列用水总量 $X_{0}^{(1)}$ ，农业用水量 $X_{1}^{(1)}$ ，工业用水量 $X_{2}^{(1)}$ ，生活用水量 $X_{3}^{(1)}$ ，生态用水量 $X_{4}^{(1)}$ ：

$X_{0}^{(1)} = [x_{0}^{(1)} (1), x_{0}^{(1)} (2), \dots, x_{0}^{(1)} (n)] = [83.3, 171.2, \dots, 1081.9]$ ，

$X_{1}^{(1)} = [x_{1}^{(1)} (1), x_{1}^{(1)} (2), \dots, x_{1}^{(1)} (n)] = [57.4, 113.6, \dots, 684]$ ，

$X_{2}^{(1)} = [x_{2}^{(1)} (1), x_{2}^{(1)} (2), \dots, x_{2}^{(1)} (n)] = [11.8, 25, \dots, 159.4]$ ，

$X_{3}^{(1)} = [x_{3}^{(1)} (1), x_{3}^{(1)} (2), \dots, x_{3}^{(1)} (n)] = [13.2, 29.4, \dots, 198.9]$ ，

$X_{4}^{(1)} = [x_{4}^{(1)} (1), x_{4}^{(1)} (2), \dots, x_{4}^{(1)} (n)] = [1.0, 3.1, \dots, 39.8]$ ，

经验证，原始数据通过光滑性检验，一次累加生成序列通过准指数检验。

(2) 构造背景值序列

用水总量 $Z_{0}^{(1)}$ ，农业用水量 $Z_{1}^{(1)}$ ，工业用水量 $Z_{2}^{(1)}$ ，生活用水量 $Z_{3}^{(1)}$ ，生态用水量 $Z_{4}^{(1)}$ ：

$Z_{0}^{(1)} = [z_{0}^{(1)} (2), z_{0}^{(1)} (3), \dots, z_{0}^{(1)} (n)] = [127.3, 215.2, \dots, 1036]$ ，

$Z_{1}^{(1)} = [z_{1}^{(1)} (2), z_{1}^{(1)} (3), \dots, z_{1}^{(1)} (n)] = [85.5, 142.7, \dots, 656.7]$ ，

$Z_{2}^{(1)} = [z_{2}^{(1)} (2), z_{2}^{(1)} (3), \dots, z_{2}^{(1)} (n)] = [18.4, 31.65, \dots, 130.2]$ ，

$Z_{3}^{(1)} = [z_{3}^{(1)} (2), z_{3}^{(1)} (3), \dots, z_{3}^{(1)} (n)] = [21.3, 36.8, \dots, 188.75]$ ，

$Z_{4}^{(1)} = [z_{4}^{(1)} (2), z_{4}^{(1)} (3), \dots, z_{4}^{(1)} (n)] = [2.05, 3.95, \dots, 36.85]$ ；

(3) 建立GM(1,1)模型的灰微分方程

用水总量： $x_{0}^{(0)} (k) + a_{0} z_{0}^{(1)} (k) = b_{0}, k = 2, 3, \dots, n$ ，

农业用水量： $x_{1}^{(0)} (k) + a_{1} z_{1}^{(1)} (k) = b_{1}, k = 2, 3, ..., n$ ，

工业用水量： $x_{2}^{(0)} (k) + a_{2} z_{2}^{(1)} (k) = b_{2}, k = 2, 3, ..., n$ ，

生活用水量： $x_{3}^{(0)} (k) + a_{3} z_{3}^{(1)} (k) = b_{3}, k = 2, 3, ..., n$ ，

生态用水量： $x_{4}^{(0)} (k) + a_{4} z_{4}^{(1)} (k) = b_{4}, k = 2, 3, ..., n$ ，

(4) 最小二乘法确定参数：

利用MATLAB软件编程求得a和b。

$a_{0} = - 0.005$ ， $b_{0} = 87.891$ ； $a_{1} = 0.005$ ， $b_{1} = 58.658$ ； $a_{2} = - 0.013$ ， $b_{2} = 13.040$ ； $a_{3} = - 0.028$ ， $b_{3} = 14.024$ ； $a_{4} = - 0.117$ ， $b_{4} = 1.615$ ；

(5) 确定GM(1,1)模型的时间响应式

${\hat{x}}_{(0)}^{(1)} (k + 1) = 17712.266 e^{0.005 k} - 17628.866$ ，

${\hat{x}}_{(1)}^{(1)} (k + 1) = - 12869.517 e^{- 0.005 k} + 12926.917$ ，

${\hat{x}}_{(2)}^{(1)} (k + 1) = - 1310.106 e^{- 0.013 k} - 1321.906$ ，

${\hat{x}}_{(3)}^{(1)} (k + 1) = 510.855 e^{0.028 k} - 497.655$ ，

${\hat{x}}_{(4)}^{(1)} (k + 1) = 14.858 e^{0.117 k} - 13.858$ ；

(6) 一阶累减还原

${\hat{x}}_{(0)}^{(0)} (k + 1) = 88.087 e^{0.005 k}$ ，

${\hat{x}}_{(1)}^{(0)} (k + 1) = 58.530 e^{- 0.005 k}$ ，

${\hat{x}}_{(2)}^{(0)} (k + 1) = 14.315 e^{- 0.011 k}$ ，

${\hat{x}}_{(3)}^{(0)} (k + 1) = 14.195 e^{0.028 k}$ ，

${\hat{x}}_{(4)}^{(0)} (k + 1) = 1.634 e^{0.117 k}$ 。

由此可得2010~2021年历年用水总量、农业用水量、工业用水量、生活用水量、生态用水量预测值见表3所示。

Table 3. Water consumption forecast data of Shaanxi Province from 2010 to 2021

表3. 陕西省2010~2021年历年用水量预测数据

5.2. 模型检验结果

对各部门用水序列进行残差检验和后验差检验，结果见表4所示。

Table 4. Model test results

表4. 模型检验结果

由表可知，生活用水量和生态用水量模型的精度等级为“好”，用水总量模型的精度等级为“合格”，但农业和工业用水量模型检验结果为“不合格”，模型精度不够，需要对其进行修正。

5.3. GM(1,1)模型修正

陕西省2010~2021年各类用水量变化如图1和图2所示。

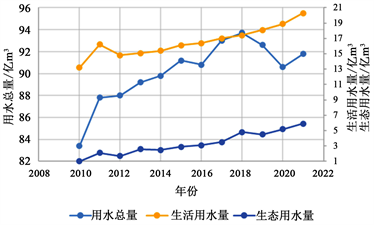
Figure 1. Changes in total water consumption, domestic water consumption, and ecological water consumption

图1. 用水总量、生活用水量、生态用水量变化

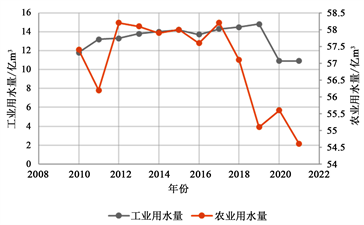
Figure 2. Changes in industrial water consumption and agricultural water consumption

图2. 工业用水量、农业用水量变化

由图1可以看出，用水总量、生活用水量和生态用水量呈平稳增长趋势，传统的GM(1,1)模型适用于分析这种稳定增长的数据，因此预测精度高。针对农业用水量和工业用水量数据，使用多种方法改进，包括参数优化和背景值优化：以 $x^{(1)} (n)$ 作为初始条件确定参数C；以使 $x^{(1)} (k) (x^{(0)} (k))$ 与 ${\hat{x}}^{(1)} (k) ({\hat{x}}^{(0)} (k))$ 离差平方和最小确定C；将原始背景值构造 $α x^{(1)} (k - 1) + (1 - α) x^{(1)} (k)$ 代入微分方程求解等。这些改进方法求得模型精度等级低，由此可知，大多学者优化初始值和背景值改进的模型不适用于用水量方面的预测。

5.3.1. 农业用水量模型修正

农业用水量受降水影响比较大，在丰水年用水量小，枯水年用水量大，此外，随着城市经济的高速发展，农业的灌溉模式也在发生改变，由图2可以看出，近十年农业用水量呈现逐年减少的趋势。因此本文采用的修正方式是建立残差GM(1,1)模型。

利用2017~2021年数据建立可建模残差尾端序列：

$ε^{(0)} (k) = x_{(1)}^{(0)} (k) - {\hat{x}}_{(1)}^{(0)} (k) = (1.500, 0.657, 1.088, 0.333, 1.080)$ ；

1-AGO序列： $ε^{(1)} (k) = (1.500, 2.157, 3.245, 3.578, 4.658)$ ；

经验证，原始数据通过光滑性检验，一次累加生成序列通过准指数检验；

模型背景值序列 $Z_{1}^{(1)'} = (1.828, 2.701, 3.411, 4.118)$ ；

灰微分方程为 $x_{1}^{(0)'} (k) + a_{1}^{'} z_{1}^{(1)'} (k) = b_{1}^{'}$ ；

最小二乘法求得 $a = - 0.071 ， b = 0.576$ ；

时间响应式为 ${\hat{x}}_{(1)}^{(1)'} (k + 1) = 9.655 e^{0.071 k} - 8.155$ ；

一阶累减还原 ${\hat{x}}_{(1)}^{(0)'} (k + 1) = 0.659 e^{0.071 k}$ ；

残差序列预测值 ${\hat{ε}}^{(0)} (k) = (1.500, 0.707, 0.7590, 0.815, 0.874)$ ；

原始数据预测值 ${\hat{X}}_{(1)}^{(0)} = 58.530 e^{- 0.005 k} - 0.659 e^{0.071 k}$ ；

则原始数据预测值 ${\hat{X}}_{(1)}^{(0)} = (58.200, 57.150, 55.429, 55.119, 54.806)$ ；

模型检验结果：平均相对误差 $\bar{Δ} = 0.004 ， C = 0.126 ， p = 1.00$ ，模型精度等级“好”。

5.3.2. 工业用水量模型修正

原始数据序列 $X_{2}^{(0)'} = (11.8, 13.2, 13.3, 13.8, 14, 14.2, 13.7, 14.3, 14.5, 14.8)$ ；

一次累加生成序列 $X_{2}^{(1)'} = (11.8, 25, 38.3, 52.1, 66.1, 80.3, 94, 108.3, 122.8, 137.6)$ ；

经验证，原始数据通过光滑性检验，一次累加生成序列通过准指数检验；

模型背景值序列 $Z_{2}^{(1)'} = (18.4, 31.65, 45.2, 59.1, 73.2, 87.15, 101.15, 115.55, 130.2)$ ；

灰微分方程为 $x_{2}^{(0)'} (k) + a_{2}^{'} z_{2}^{(1)'} (k) = b_{2}^{'}$ ；

最小二乘法求得 $a = - 0.013 ， b = 13.040$ ；

则时间响应式为 ${\hat{x}}_{(2)}^{(1)'} (k + 1) = 1034.523 e^{0.013 k} - 1022.723$ ；

一阶累减还原 ${\hat{x}}_{(2)}^{(0)'} (k + 1) = 13.107 e^{0.013 k}$ ；

模型检验结果：平均相对误差 $\bar{Δ} = 0.010 ， C = 0.237 ， p = 1.00$ ，模型精度等级“好”。

5.4. 用水量预测

采用用水总量、生活用水量、生态用水量灰色GM(1,1)预测模型，以及农业用水量、工业用水量修正GM(1,1)预测模型预测陕西省2022~2026年未来五年的用水总量、农业用水量、工业用水量、生活用水量以及生态用水量，预测结果见表5所示。

Table 5. Water consumption projections for 2022~2026

表5. 2022~2026年用水量预测

为进一步检验该模型的合理性和准确性，与传统GM(1,1)模型以及文献 [13] 中灰色组合模型进行预测误差分析。选用近5年即2017~2021数据作为测试数据，计算相对误差见表6所示。

Table 6. Comparison of prediction error results of different models

表6. 不同模型预测误差结果比较

由表6可以看出，本文提出的改进灰色模型预测误差最小，结果更合理，说明该模型对陕西省用水量进行预测具有很好的适用性。

6. 结论

(1) 在前人研究的基础上，本文采用改进GM(1,1)模型，用水总量和各部门用水量预测模型精度都有很大提高。从结果来看，陕西省用水总量呈波动增长趋势，随着人民生活水平的提高，居民生活用水不断增加；城市化进程的加快促进工业发展，工业用水量也逐年增长，随之也加大生态环境保护用水量；由于农业节水灌溉技术的不断优化，农业用水量逐年下降。

(2) 本文针对陕西省2010~2021年历年用水量所建立的预测模型精度等级高，对未来5年用水量预测结果真实有效，可为供水规划决策提供可靠的数据支撑；此外，本研究重点是通过实践验证对于用水量此类呈平稳增长趋势的数据适用传统模型和残差修正模型，弥补了前人在实践上的不足。

(3) 灰色GM(1,1)预测模型是存在缺陷的，其预测数据是单调递增或单调递减，但实际被预测因素数据可能呈波动性变化，因此在实际应用中需进一步改进。

基金项目

陕西省自然科学基础研究计划项目(2021JLM-52)。

参考文献

[1]	伍德权, 杨延梅, 付宇. 基于灰色系统理论的贵阳市城市用水总量预测[J]. 南昌工程学院学报, 2022, 41(1): 40-46.
[2]	谢锦彪, 欧毓毅, 凌捷. 改进的灰色GM(1, 1)预测模型[J]. 计算机工程与设计, 2015, 36(5): 1380-1384.
[3]	闫海霞, 王秋萍, 郭佳丽. 基于飞蛾火焰优化算法的改进GM(1, 1)模型[J]. 西安理工大学学报, 2022, 38(1): 69-74.
[4]	江艺羡, 张岐山. GM(1, 1)模型背景值的优化[J]. 中国管理科学, 2015, 23(9): 146-152.
[5]	邓聚龙. 灰色预测与决策[M]. 武汉: 华中工学院出版社, 1986: 214-313.
[6]	刘思峰, 曾波, 刘解放, 等. GM(1, 1)模型的几种基本形式及其适用范围研究[J]. 系统工程与电子技术, 2014, 36(3): 501-508.
[7]	陈鹏宇, 邓宏伟. GM(1, 1)模型的改进现状及应用[J]. 统计与决策, 2019, 35(6): 80-82.
[8]	刘思峰, 邓聚龙. GM(1, 1)模型的适用范围[J]. 系统工程理论与实践, 2000(5): 121-124.
[9]	徐宁, 党耀国, 丁松. 基于误差最小化的GM(1, 1)模型背景值优化方法[J]. 控制与决策, 2015, 30(2): 283-288.
[10]	李峥. 改进背景值的GM(1, 1)优化模型[J]. 科技信息, 2010(19): 449-450.
[11]	吕学梅, 张磊, 李炳文, 等. 灰色GM(1, 1)及其残差修正模型在不同程度春旱发生年份预测中的应用[J]. 中国农业气象, 2010, 31(3): 479-483.
[12]	党云刚. 陕西省水资源空间均衡状态分析与协调研究[J]. 华北水利水电大学学报(自然科学版), 2022, 43(3): 36-42+74.
[13]	王有娟, 冯卫兵, 李奥典. 基于灰色组合模型的浙江省需水量预测[J]. 水电能源科学, 2015, 33(3): 22-26.

为你推荐

友情链接