1. 引言
非线性动力学和非线性波动的研究对于解决物理学、化学、生物学和地球物理学中遇到的复杂问题有着极其重要的意义 [1] [2] [3] 。固体结构中的非线性波往往蕴含着极其丰富多彩的物理现象,这些现象只有借助研究非线性波动特性,才能得到进一步认识。因此,开展该类研究有着十分重要的学术价值和工程应用前景 [4] [5] [6] 。
对于梁中的线性弯曲波,在Bernoulli-Euler梁初等理论下的运动方程忽略了剪切变形的影响,即在变形过程中横截面始终保持平面并垂直于中心轴,并且不考虑梁的转动惯性效应的影响 [7] 。为了研究梁中的非线性弯曲波的传播规律,我们需要考虑转动惯性的影响和由梁的大挠度引起的几何非线性效应的影响 [8] 。在本文中,我们采用Lagrange物质描述,取变形前的梁轴为x轴,中性轴为y轴,梁发生弯曲的方向取为z轴,如图1所示 [4] 。
由于在x方向没有外力作用,我们采用如下位移表达式:
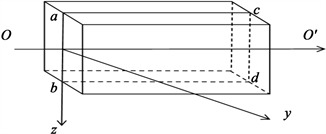
Figure 1. Bending of beams under assumption of plane section
图1. 平截面假定下梁的弯曲
其中W为z方向的挠度,
分别表示
方向的位移 [9] 。利用变分运算,我们可以得到非线性弯曲波的波动方程:
其中c0为纵向的弹性波波速,r1为截面对中性轴的回转半径。该方程同时包含了由梁的大挠度引起的非线性效应和梁的转动惯性引起的几何弥散效应,当这两种效应达到平衡时,有稳定传播的孤波或冲击波 [10] [11] 。
设该方程的解为
其中
为前一项的共轭。分别对
,
,
近似,可得到非线性薛定谔方程 [12] :
我们考虑高阶项的影响,得到混合非线性薛定谔方程 [13] :
本文进一步考虑非均匀介质下的模型,即变系数混合非线性薛定谔方程:
(1)
以非线性偏微分方程理论为基础,借助符号计算软件,完成了以下三个方面的工作:一、从方程(1)的Lax对出发,构造出一阶及N阶达布变换;二、运用达布变换,得到了方程在不同初始解下的一、二阶孤子解及呼吸子解;三、令呼吸子的周期趋于无限大,得到了方程的一阶及高阶怪波解。对于高阶怪波,进一步通过改变控制函数的取值,得到了三角型二、三阶怪波和圆型三阶怪波。
2. 变系数混合非线性薛定谔方程的达布变换
2.1. 方程的Lax可积性
我们可以证明方程(1)是Lax可积的,并且方程对应的Lax对可以表示为:
, (2a)
, (2b)
其中
,(3a)
, (3b)
,
,
这里 是谱参数,
(T表示矩阵的转置)。事实上,
满足
,则可得到零曲率方程:
, (4)
其中
,由此方程可得到变系数混合非线性薛定谔方程(1)。
2.2. 一阶达布变换
经过计算,我们得到方程(1)的一阶达布变换矩阵满足以下形式 [14] :
, (5)
其中
, (6a)
, (6b)
, (6c)
. (6d)
矩阵T满足方程组
,
,
其中
和
是将矩阵
和
中的函数
用新函数
代替后的新矩阵。
根据上述方程组,我们得到方程(1)的一阶达布变换:
. (7)
2.3. N阶达布变换
方程(1)的N阶达布变换矩阵有以下形式:
, (8)
令
,
.
通过计算可得:
是由将
的第n列换成
后的矩阵为分子和
为分母组成的;
是由将
的第2n列换成
后的矩阵为分子和
为分母组成的;
是由将
的第n列换成
后的矩阵为分子和
为分母组成的;
是由将
的第2n列换成
后的矩阵为分子和
为分母组成的。
T仍然满足以下条件:
,
,
其中
,
,
,
仍然保持原来的形式,但
已经变成
,因此得到方程(2)的N阶达布变换:
. (9)
3. 变系数混合非线性薛定谔方程的孤子解
3.1. 一阶孤子解
本节我们选取变系数混合非线性薛定谔方程的零种子解
,将其代入到Lax对中,系数矩阵变为:
,
.
设
是方程组(2)当
时的解,则
的具体表达式可通过求解方程组(2)求得:
, (10)
其中
为常数。其共轭的具体形式为:
. (11)
此时方程(2)的一阶达布变换
的具体表达式为:
. (12)
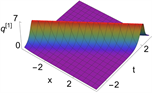
将表达式(10)和(11)代入(12)中,并对参数赋值,可以得到方程(1)的一阶孤子解。其动力学特征如图2所示。
3.2. 二阶孤子解
我们仍然选取变系数混合非线性薛定谔方程的零种子解
来构造二阶孤子解。我们需要构造Lax对(2)的两组解:
和
,分别对应
和
。类似于3.1节,这两组解的具体形式如下:
 (a)
(a) 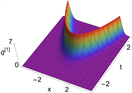 (b)
(b)  (c)
(c)  (d)
(d)  (e)
(e) 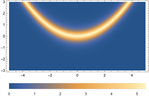 (f)
(f) 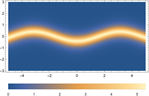 (g)
(g)  (h) (a)
; (b)
;(c)
; (d)
.
(h) (a)
; (b)
;(c)
; (d)
.
Figure 2. The first-order soliton solution of Eq. (1). (a)~(d) are 3D plots, and (e)~(h) are density plots corresponding to (a)~(d)
图2. 方程(1)的一阶孤子解。(a)~(d)为3D图,(e)~(h)为(a)~(d)对应的密度图
, (13)
. (14)
根据2.3节,方程(1)二阶达布变换为:
. (15)
其中
、
、
、
的具体表达形式可根据2.3节求得。
通过对参数的赋值,我们可以得到方程(1)的二阶孤子解。其动力学特征如图3、图4所示:
 (a)
(a) 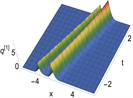 (b)
(b) 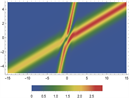 (c)
(c)  (d)(a)
; (b)
.
(d)(a)
; (b)
.
Figure 3. 2-order soliton solutions of Eq. (1). (a) and (b) are 3D plots, and (c) and (d) are density plots corresponding to (a) and (b)
图3. 方程(1)的二阶孤子解。(a)和(b)为3D图,(c)和(d)为(a)和(b)对应的密度图
 (a)
(a)  (b)
(b)  (c)
(c) 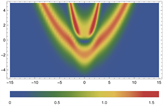 (d)
(d) 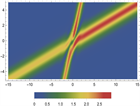 (e)
(e)  (f)(a)
; (b)
;(c)
.
(f)(a)
; (b)
;(c)
.
Figure 4. 2-order soliton solutions of Eq. (1). (a)~(c) are 3D plots, and (d)~(f) are density plots corresponding to (a)~(c)
图4. 方程(1)的二阶孤子解。(a)~(c)为3D图,(d)~(f)为(a)~(c)对应的密度图
4. 变系数混合非线性薛定谔方程的呼吸子解
在本节中,我们将应用达布变换来讨论变系数混合非线性薛定谔方程的呼吸子解。设方程(1)的种子解为:
,
,
其中
且
,
是实函数。将其代入到方程(1)中,可得到色散关系:
. (16)
由
,
其中
,可得到
. (17)
设
,
将其代入方程组(17)中求解可得:
,(18)
其中
,
。
4.1. 一阶呼吸子
设
是方程组(2)当
时的解,则
, (19)
其中
,
,
,
.
其共轭的具体形式为:
, (20)
其中
,
,
,
.
将表达式(19)和(20)代入一阶达布变换(7)中,可以求出方程(1)在平面波背景下的一阶呼吸子解,如图5所示。
 (a)
(a)  (b)
(b) 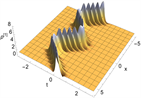 (c)
(c)  (d)
(d)  (e)
(e) 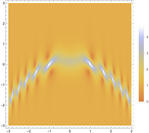 (f)
(f) 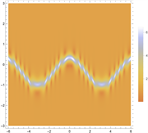 (g)
(g)  (h)
(h)
(a)
;
(b)
;
(c)
;
(d)
.
Figure 5. 1-order breather solutions of Eq. (1). (a)~(d) are 3D plots, and (e)~(h) are density plots corresponding to (a)~(d)
图5. 方程(1)的一阶呼吸子解。(a)~(d)为3D图,(e)~(h)为(a)~(d)对应的密度图
4.2. 二阶呼吸子
设
和
分别为
和
时方程组(2)的解,则
, (21a)
, (21b)
其中
,
,
,
,
,
,
,
.
将表达式(2)代入高阶达布变换(9)并取
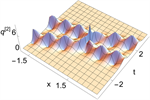
,我们可以得到平面波背景下的二阶呼吸子解,如图6所示。
 (a)
(a) 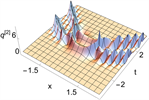 (b)
(b) 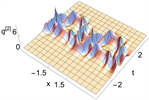 (c)
(c) 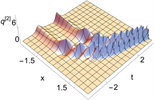 (d)
(d) 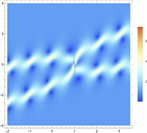 (e)
(e)  (f)
(f) 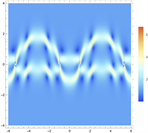 (g)
(g) 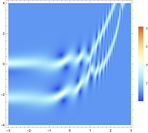 (h)
;(a)
; (b)
; (c)
; (d)
.
(h)
;(a)
; (b)
; (c)
; (d)
.
Figure 6. 2-order breather solutions of Eq. (1). (a)~(d) are 3D plots, and (e)~(h) are density plots corresponding to (a)~(d)
图6. 方程(1)的二阶呼吸子解。(a)~(d)为3D图,(e)~(h)为(a)~(d)对应的密度图
5. 变系数混合非线性薛定谔方程的怪波解
在本节中,我们研究变系数混合非线性薛定谔方程的怪波解。首先将呼吸子的周期变为无限大,即频率趋于零:
.
因为当
,
,
时,
。所以,为了使频率趋于0,我们取
,其中g是一个小实参数。
设方程(1)的种子解为:
,
.
取
是方程组(2)当
时的解,其可表示为:
(22)
其中
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
.
5.1. 一阶怪波解
将表达式(22)代入一阶达布变换(7)中,对矩阵中的每一项在
处进行泰勒展开,并提出
的系数进行行列式计算,如:
.
同理可求得
,
,
,最后再将其代入一阶达布变换
,我们可以得到一阶怪波解的具体表达式,其动力学行为如图7所示。在图7中,我们可以观察到怪波是由一个峰和两个谷组成的,它们在时间和空间上都是局域的,这正好说明了怪波的特征——突然出现又凭空消失 [15] 。
 (a)
(a)  (b)
(b)  (c)
(c) 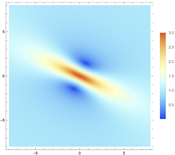 (d)(a)
,
,
,
,
,
;(c)
,
,
,
,
,
.
(d)(a)
,
,
,
,
,
;(c)
,
,
,
,
,
.
Figure 7. 1-order rogue wave solution of Eq. (1). (a) and (c) are 3D plots, and (b) and (d) are density plots corresponding to (a) and (c)
图7. 方程(1)的一阶怪波解。(a)和(c)为3D图,(b)和(d)为(a)和(c)对应的密度
5.2. 二阶怪波解
将表达式(22)代入达布变换(9)中,对矩阵中的每一项在
处进行泰勒展开,并提出
,
的系数进行行列式计算,可以求得
,
,
,最后将其代入二阶达布变换
,可以得到基础型二阶怪波解的具体表达式,其动力学行为如图8所示。
通过改变
与
的取值,我们可进一步改变怪波的组合方式。如令
,
,我们可以得到三角型二阶怪波,其动力学行为如图9所示。
5.3. 高阶怪波解
将表达式(22)代入达布变换(9)中,同样将矩阵中的每一项在
处进行泰勒展开,并提出
,
,
的系数进行行列式计算,可以求得
,
,
,再将其代入三阶达布变换
中,最终得到基础型三阶怪波解的具体表达式。通过改变
与
,
的取值,我们可得到多种怪波的组合方式。令,
,
可以得到三角型三阶怪波解;令
,
,可以得到圆型三阶怪波解。以上三种类型的三阶怪波的动力学行为如图10所示。
 (a)
(a) 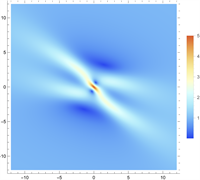 (b)
(b)  (c)
(c) 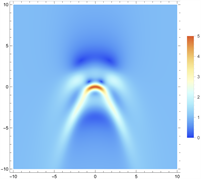 (d)(a)
,
,
,
,
,
;(c)
,
,
,
,
,
.
(d)(a)
,
,
,
,
,
;(c)
,
,
,
,
,
.
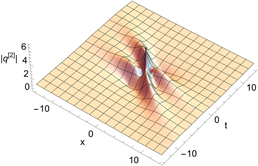
Figure 8. Fundamental 2-order rogue wave solution of Eq. (1). (a) and (c) are 3D plots, and (b) and (d) are density plots corresponding to (a) and (c)
图8. 方程(1)的基础型二阶怪波解。(a)和(c)为3D图,(b)和(d)为(a)和(c)对应的密度
 (a)
(a) 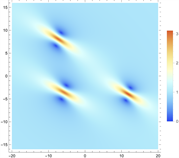 (b)
(b)  (c)
(c) 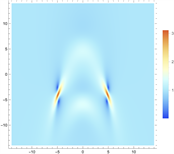 (d)(a)
,
,
,
,
,
;(b)
,
,
,
,
,
.
(d)(a)
,
,
,
,
,
;(b)
,
,
,
,
,
.
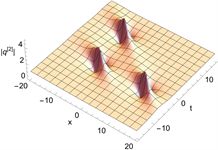
Figure 9. Triangular 2-order rogue wave solution of Eq. (1). (a) and (c) are 3D plots, and (b) and (d) are density plots corresponding to (a) and (c)
图9. 方程(1)的基础型三阶怪波解。(a)和(c)为3D图,(b)和(d)为(a)和(c)对应的密度
 (a)
(a)  (b)
(b) 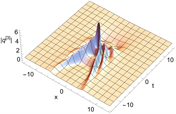 (c)
(c)  (d)
(d)  (e)
(e)  (f)
(f) 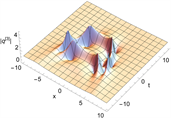 (g)
(g)  (h)
(h) 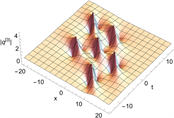 (i)
(i) 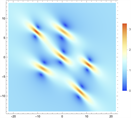 (j)
(j) 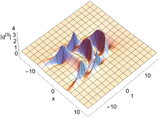 (k)
(k)  (l)
,
,
,
,
; (a), (e), (i):
; (c), (g), (k):
.
(l)
,
,
,
,
; (a), (e), (i):
; (c), (g), (k):
.
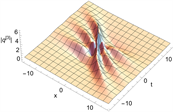
Figure 10. 3-order rogue wave solutions of Eq. (1). (a)~(d) are basic types, (e)~(h) are triangular types, and (i)~(l) are circular types. (a), (c), (e), (g), (i), (k) are 3D plots, (b), (d), (f), (h), (j), (l) are density plots corresponding to (a), (c), (e), (g), (i), and (k)
图10. 方程(1)的三阶怪波解。(a)~(d)为基础型,(e)~(h)为三角型,(i)~(l)为圆型。(a), (c), (e), (g), (i), (k)为3D图,(b), (d), (f), (h), (j), (l)为(a), (c), (e), (g), (i), (k)所对应的密度图
6. 结论
本文主要以非均匀弹性梁介质中的变系数混合非线性薛定谔方程为研究对象,通过达布变换方法,求得了该方程的一、二阶孤子解、呼吸子解,一、二、三阶怪波解,具体如下:
1) 从变系数混合非线性薛定谔方程的Lax对出发,构造出一阶达布变换,并将其推广到N阶,并得到了方程在不同系数下的一、二阶孤子解,并借助数学软件绘制图像,分析其动力学性质。
2) 选取方程的平面波解,得到了色散关系,在不同系数下求出了方程的一、二阶呼吸子解,并利用图像描绘了其动力学性质。
3) 令呼吸子的周期趋于无限大,得到了一阶及高阶怪波解。对于高阶怪波,通过改变控制函数的取值,得到了三角型二、三阶怪波和圆型三阶怪波,并由图像观察到了怪波具有局域性的特征。
4) 论文的结果可为非均匀弹性梁介质中的怪波实验研究提供理论支撑。
基金项目
山西省国际合作基地与平台项目(202104041101019)。
NOTES
*通讯作者。