一种广义决策保持的快速启发式属性约简算法

A Fast Heuristic Attribute Reduction Algorithm for Generalized Decision Preservation

摘要: 属性约简是粗糙集理论的重要概念之一，旨在获得一个可以保持原始信息系统分类能力的最小属性子集。广义决策保持约简是粗糙集中的属性约简方法之一，其目标为维护决策系统中的决策结果，确保在约简过程中不丢失原始决策。这意味着约简后的系统仍可正确地进行决策，而决策规则的有效性和决策能力得以保持。传统的广义决策保持启发式属性约简算法注重算法的有效性，而算法的效率有待优化。传统算法在计算广义决策保持相似度时需多次遍历每个对象的等价类与决策类，存在大量的重复计算。为了克服这个问题，我们通过引入哈希表来存储每个对象的等价类与其广义决策，使得计算广义决策保持相似度时可针对计算对象直接得出结果而不是依次遍历，由此提出了广义决策保持的快速启发式属性约简算法。最后，通过6组UCI数据集验证了本文提出算法的有效性与高效性。

Abstract: Attribute reduction is one of the key concepts in rough set theory, aimed at obtaining the minimal subset of attributes that retains the classification capability of the original information system. Generalized Decision-Preserving Reduction is a method of attribute reduction within rough set theory, which focuses on maintaining the outcomes of decision-making systems, ensuring that the original decisions are not lost during the reduction process. This implies that the reduced system can still make correct decisions, with the effectiveness and capability of decision rules maintained. Traditional algorithms prioritize effectiveness, but their efficiency needs improvement. These conventional algorithms require multiple traversals through each object’s equivalence class and decision class to compute the similarity degree for generalized decision preservation, leading to extensive redundant computations. To overcome this issue, we introduce the use of hash tables to store each object’s equivalence class and its generalized decision, allowing direct computation of similarity degree for generalized decision preservation for a computational object, rather than sequential traversals, thereby accelerating the algorithm. Finally, the efficacy and efficiency of the proposed algorithm are validated through six sets of UCI datasets.

1. 引言

1982年波兰数学家Pawlak [1] [2] 为了处理不准确、不确定的数据，提出了粗糙集理论。在粗糙集理论中，属性约简 [3] - [8] 是一个关键概念，其主旨在于通过识别数据集中最关键的属性集，在不影响原始分类能力的情况下简化信息系统的表示，减少冗余属性，提高对大规模数据和高维数据的处理效率。广义决策保持约简 [9] [10] [11] 是粗糙集理论属性约简中的一个重要的算法，旨在选择的最小属性子集可以保持决策能力，提高决策系统的效率和可解释性。与传统属性约简侧重于等价关系和近似空间不同，广义决策保持约简强调在简化属性集的同时，确保维持决策系统的原始决策，这有助于保证约简后属性子集的可解释性，使得约简结果更容易为人理解和接受。

随着数据集规模的不断增大和特征维度的提高，传统的属性约简算法可能面临巨大的计算复杂性和资源消耗。而在实际应用中，如大规模数据挖掘和智能决策系统，对计算时间的迅速响应是至关重要的。在这一背景下，研究者致力于设计高效的属性约简算法，以加速属性约简的过程 [12] [13] [14] [15] [16] 。通过降低计算复杂性，这些改进不仅有助于在有限时间内处理大规模数据，同时也提升了属性约简方法的实用性和可扩展性。

由于广义决策保持约简算法的计算过程需计算每个对象所在等价类的广义决策相似度，而计算广义决策相似度需多次遍历全部决策类并依次计算结果，若使等价类与决策类一一对应，则可通过单次计算直接得到广义决策相似度，从而避免了重复计算。本文在广义决策保持启发式属性约简的基础上，提出了可使每个等价类与其相关决策类对应的广义决策哈希表，由此实现了广义决策保持的快速启发式属性约简算法。最后，经过实验证明了本文所提算法的高效性。

2. 基本概念

2.1. Pawlak经典粗糙集理论

定义1. [1] 给定信息系统IS是一个四元组： $IVDS=\left(U,A,V,f\right)$ ，其中U是一个非空有限集合称为论域，A表示一个非空有限的属性集合，V表示的是属性集合A的值域，f是一个映射函数，其中 $f:U\times AT\to V$ ， $f\left(x,a\right)$ 表示对象 $x\in U$ 在属性 $a\in A$ 上的取值，简记为 $a\left(x\right)$ 。若属性集A可分为条件属性C与决策属性D，即 $A=C\cup D$ ，则四元组 $\left(U,A=C\cup D,V,f\right)$ 为一个决策系统， $f\left(x,d\right)$ 表示对象x在属性 $d\in D$ 上的取值，简记为 $d\left(x\right)$ 。

定义2. [1] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ，若 $x_a,x_b\in U$ ，则属性集Q下的不可分辨关系定义为：

$Ind\left(P\right)=\left\{\left(x_a,x_b\right)\in U\times U|\forall p\in P,p\left(x_a\right)=p\left(x_b\right)\right\}$ (1)

显然， $Ind\left(Q\right)$ 是对称的、传递的、自反的等价关系。对于论域U， $Ind\left(P\right)$ 可将其划分为不同等价类，即 $U/Ind\left(P\right)=U/P=\left\{{\left[x\right]}_P|x\in U\right\}$ ，其中 ${\left[x\right]}_P=\left\{y\in U|\left(x,y\right)\in Ind\left(P\right)\right\}$ 。对于决策属性D，不可分辨关系划分所得的U/D中的对象被称为决策类。

定义3. [1] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ， $D_m\subseteq U/D$ ，属性集P对于 $D_m$ 的上近似与下近似的定义为：

$\underset{\_}{P}\left(D_m\right)=\left\{x|{\left[x\right]}_P\subseteq D_m\right\}=\cup \left\{{\left[x\right]}_P|{\left[x\right]}_P\subseteq D_m\right\}$ (2)

$\bar{P}\left(D_m\right)=\left\{x|{\left[x\right]}_P\cap D_m\ne \varnothing \right\}=\cup \left\{{\left[x\right]}_P|{\left[x\right]}_P\cap D_m\ne \varnothing \right\}$ (3)

对于 $\forall P\subseteq C$ ，其下近似中的对象为确定属于 $D_m$ ，其上近似中的对象代表其可能属于 $D_m$ 。由下近似与上近似可将论域U划分为三个区域，即正域、边界域、负域，定义如下：

$Po{s}_P=\underset{\_}{P}\left(D_m\right)$ (4)

$Bn{d}_P=\bar{P}\left(D_m\right)-\underset{\_}{P}\left(D_m\right)$ (5)

$Ne{g}_P=U-\bar{P}\left(D_m\right)$ (6)

其中正域与负域分别代表了确定属于 $D_m$ 的对象与确定不属于 $D_m$ 的对象，为确定性信息，而边界域代表了可能属于 $D_m$ 的对象，为不确定性信息。此外，论域U与正域、边界域、负域的关系为：

$U=Po{s}_P\left(D_m\right)+Bn{d}_P\left(D_m\right)+Ne{g}_P\left(D_m\right)$ (7)

2.2. 基于广义决策保持的启发式属性约简算法

定义4. [11] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ，对于 $x_a\in U$ ， ${\left[x_a\right]}_P\in U/P$ ，对象 $x_a$ 在属性集P下的广义决策为：

${\delta }_P\left(x_a\right)=\left\{d\left(x_b\right)|x_b\in {\left[x_a\right]}_P\right\}$ (8)

定义5. [11] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ， $x_a\in U$ ，若 ${\left[x_a\right]}_P\in U/P$ ， ${\left[x_a\right]}_C\in U/C$ ，广义决策保持的相似度定义为：

$Sim\left(P,C\right)=\{\begin{array}{ll}\frac{\left|{\cup }_{i=1}^{\left|U\right|}\left({\left[x_a\right]}_P\cap {\left[x_a\right]}_C\right)\right|}{\left|U\right|},\hfill & {\delta }_P\left(x_a\right)={\delta }_C\left(x_a\right)\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$ (9)

定义6. [11] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，当且仅当以下两个条件成立时， $P\subseteq C$ 为此决策系统的一个广义决策保持约简：

1) 联合充分性： $Sim\left(P,C\right)=1$ ；

2) 个体必要性： $\forall Q\subset P$ ，满足 $Sim\left(P,Q\right)\ne 1$ 。

定义7. [11] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ， $p\in P$ ，广义决策保持的内部属性重要度定义为：

$Si{g}^{inner}\left(p,P,C\right)=Sim\left(P,C\right)-Sim\left(P-\left\{p\right\},C\right)$ (10)

定义8. [11] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ，若 $\exists p\in P$ 存在 $Si{g}^{inner}\left(p,P,C\right)>0$ ，则 $p\in Core$ 。

定义9. [11] 在决策系统 $DS=\left(U,A=C\cup D,V,f\right)$ 中，设 $\forall P\subseteq C$ ， $p\in P$ ，广义决策保持的内部属性重要度定义为：

$Si{g}^{outer}\left(p,P,C\right)=Sim\left(P\cup \left\{p\right\},C\right)-Sim\left(P,C\right)$ (11)

基于上述定义，可知广义决策保持的前向启发式属性约简算法(A Forward Greedy Reduction Algorithm for Generalized Decision Preservation, FGRAG) [11] 如表1所示。

Table 1. A forward greedy reduction algorithm for generalized decision preservation (FGRAG)

表1. 广义决策保持的前向启发式属性约简算法

由于计算广义决策保持的相似度时，对于 ${\delta }_P\left(x\right)={\delta }_C\left(x\right)$ 的对象需要遍历所有等价类才可得出 $Sim\left(P,C\right)$ ，即时间复杂度为 $O\left(\left|U\right|\right)$ ，对于每个符合条件的对象，总体时间复杂度为 $O\left({\left|U\right|}^2\right)$ 。因此，在上述FGRAG算法中，步骤1与步骤2的时间复杂度为 $O\left(\left|C\right|\left|U\right|+\left|C\right|\left(\left|C\right|\left|U\right|+{\left|U\right|}^2\right)\right)$ ，步骤3的时间复杂度为 $O\left(\left|C\right|\left({\left|C\right|}^2\left|U\right|+{\left|U\right|}^2\right)\right)$ ，步骤4的时间复杂度为 $O\left(\left|C\right|\left(\left|C\right|\left|U\right|+{\left|U\right|}^2\right)\right)$ ，步骤5的时间复杂度为 $O\left(1\right)$ 。因此，FGRAG算法的时间复杂度为 $O\left({\left|C\right|}^3\left|U\right|+\left|C\right|{\left|U\right|}^2\right)$ 。

3. 广义决策保持的快速启发式属性约简算法

由于计算广义决策保持的相似度时需多次遍历等价类，所以本节主要通过实现广义决策保持的相似度的快速计算方法从而加速传统广义决策保持的启发式属性约简算法。

在计算广义决策保持的相似度前，需计算属性子集 $P\subseteq C$ 下的广义决策哈希表，如表2所示：

Table 2.Algorithm for computing generalized decision hash tables (GDHT)

表2. 广义决策哈希表的计算算法

在算法GDHT中，由于仅遍历一次论域，所以时间复杂度为 $O\left(\left|C\right|\left|U\right|\right)$ 。在算法结束后，广义决策哈希表 $Has{h}_P$ 中所存储的内容为键与其对应的值，其中键为由不同等价类的条件属性值组成的字符串，值为该条件属性值下的等价类与其广义决策。得益于哈希表查找的高效性，若已知某一对象的条件属性值，则可在 $O\left(1\right)$ 的时间复杂度下确定其所属的等价类与其广义决策。

此外，若 $P=C$ ，则 $Has{h}_C$ 为一个特殊的广义决策哈希表，由于在后续计算过程中需频繁查找 $Has{h}_C$ 且 $Has{h}_C$ 仅需计算一次，所以后续算法均默认 $Has{h}_C$ 的存在。对于 $P\subseteq C$ ，通过 $Has{h}_C$ 与 $Has{h}_P$ 可得广义决策保持的相似度的快速计算算法，如表3所示：

Table 3.A fast algorithm for computingsimilarity degree for generalized decision preservation(FCSG)

表3. 广义决策保持的相似度的快速计算算法

在算法FCSG中，通过哈希表查找的高效性可快速定位指定对象的等价类与广义决策，而不用重复遍历。算法时间复杂度为 $O\left(\left|U\right|\right)$ 。由此可得出广义决策保持的快速启发式属性约简算法(A Fast Heuristic Attribute Reduction Algorithm for Generalized Decision Preservation, FAGD)，如表4所示：

Table 4.A fast heuristic attribute reduction algorithm for generalized decision preservation (FAGD)

表4. 广义决策保持的快速启发式属性约简算法

在算法FAGD中，步骤1与步骤2的时间复杂度为 $O\left(\left|C\right|\left|U\right|+\left|C\right|\left(\left|C\right|\left|U\right|+\left|U\right|\right)\right)$ ，步骤3的时间复杂度为 $O\left(\left|C\right|\left({\left|C\right|}^2\left|U\right|+\left|C\right|\left|U\right|\right)\right)$ ，步骤4的时间复杂度为 $O\left(\left|C\right|\left(\left|C\right|\left|U\right|+\left|C\right|\left|U\right|\right)\right)$ ，步骤5的时间复杂度为 $O\left(1\right)$ 。因此，FAGD算法的时间复杂度为 $O\left({\left|C\right|}^3\left|U\right|\right)$ ，优于算法FGRAG的 $O\left({\left|C\right|}^3\left|U\right|+\left|C\right|{\left|U\right|}^2\right)$ 。

4. 实验分析

本实验选取6个UCI数据集进行约简效率的对比，数据集的详细信息如表5所示。本节主要对传统的广义决策保持的前向启发式属性约简算法(FGRAG)与本文提出的广义决策保持的快速启发式属性约简算法(FAGD)约简效率进行对比。本实验在i7-8750h处理器、16.00 GB内存和MacOS 12.6操作系统下进行。

Table 5. DatasetInformation

表5. 实验使用的数据集

约简效率

传统的广义决策保持的前向启发式属性约简算法(FGRAG)与本文提出的广义决策保持的快速启发式属性约简算法(FAGD)按照论域规模变化的时间效率对比图。对象规模变化规则如下：将论域平均划分为5份。横坐标表示参与实验的论域规模，即原始数据的20%、40%、60%、80%、100%。纵坐标是约简所消耗的时间单位是秒，红色是广义决策保持的前向启发式属性约简算法(FGRAG)，蓝色是广义决策保持的快速启发式属性约简算法(FAGD)。

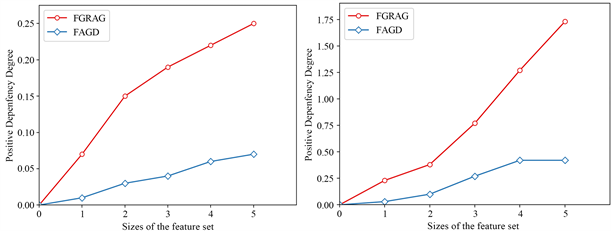
(a) Breast-w (b) Vehicle

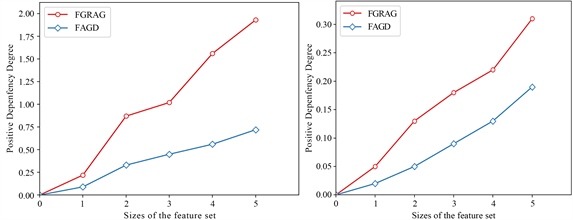(c) German (d)House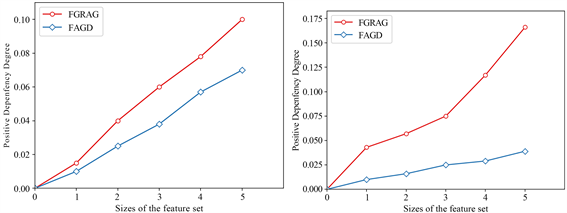(e) Solar Flare (f) Primary-tumor

Figure 1. Comparison of reduction efficiency

图1. 约简效率对比

由图1可知，当论域规模较小时，FAGD算法与FGRAG算法的效率差别不大。当随着论域规模逐渐增加时，两种算法的执行时间均有上升，但是本文提出的算法随着论域规模的增加变化比较均匀，稳定性更好。本文提出的FAGD算法的折线始终保持在FGRAG算法折线的下方，表明FAGD算法一直保持较好的效率。当论域规模较大时，两种算法直接的差距更为明显，以数据集Vehicle为例，FGRAG算法运行时间为1.73秒，而FAGD算法仅为0.42秒，仅为FGRAG算法的四分之一左右，相对来说可以证明本文提出的算法更加适用于大规模的数据集。因此，本文提出的FAGD算法与FGRAG算法相比更具稳定性与高效性性。

5. 结论

在本文中，首先提出了广义决策哈希表概念，通过此概念实现了广义决策保持的相似度的快速计算算法，并通过加速广义决策保持相似度的计算效率实现了广义决策保持的快速启发式属性约简算法(FAGD)。最后通过选取的六组UCI数据集验证了算法的高效性。从实验结果可以看出，本文所提的算法相比于传统算法效率更高。

基金项目

本文受烟台市科技计划项目(编号：2022XDRH016)的资助。